小议建模素养在教学中的渗透*

☉江苏省海门市四甲中学 王宗艳

小议建模素养在教学中的渗透*

☉江苏省海门市四甲中学 王宗艳

2017年年初新课程标准已经在酝酿出炉，从三维目标到今天提出全新的核心素养角度，数学教学需要做出进一步的与时俱进的改革.遵从教育的核心素养，数学学科核心素养也相应提出.众所周知，数学学科核心素养提出了六条原则，与教材和大纲较为吻合地提出了数学建模素养，这是一直以来教材所推崇的如何利用数学知识解决实际问题的体现.

数学建模素养是怎么培养和建立？人民教育出版社章建跃近期在中小学数学杂志尾页上就新版教材诸多应用型问题的使用这样评价：现在的教材编写特别注重了对应用型问题的编制，这一点是依据课程标准大纲对于数学应用性要求的体现，也直接提高了学生对于数学实用性的关注，与建模素养的培养和建立休戚相关.笔者认为，要将建模素养在教学中渗透必须进行合理的教学选择、设计，知识点如何安排和在具体情境问题中体会，是建模素养教学实施的关键.

一、从应用问题中渗透建模

数学是一门研究数量关系本质的学科.从建模最初级别层次的理解，可以从应用型问题入手.可以这么说，应用型问题是数学知识为载体，以具体情境为依托的问题，其抛开情境自然而然的是研究数学化的问题.这对于学生而言，从问题中挖掘数学的想法是比较自然的，难点在于如何挖掘？如何看到问题涉及的是怎么样的数学知识，如图1.

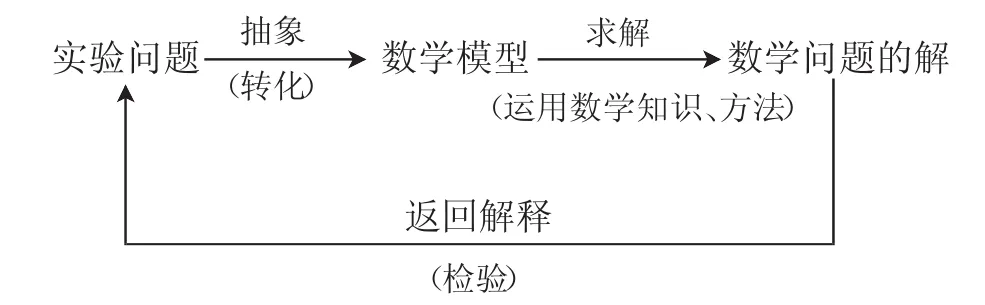
图1

问题1：在购买一件价格为5000元的商品时，采用天猫分期付款，那么在一年内将款全部付清的前提下，商家提出了下表所示的几种付款方案，以供顾客选择：（1）分期付款中规定每期所付款额相同；（2）每月利息按复利计算.

思考：对于分期付款是生活现实的一个问题，按照银行利息计算方式，我们需要从数列角度思考.将问题的情境抽离，我们发现其本质是数列求和问题，需要关注的是问题所选择的是等比数列求和.

解析：以6次还清作为研究对象，来分析两种不同的建模思路.

（1）设每期应付款为x元，5000元12个月后的本息和为5000（1+0.8%）12，分期付款各期所付款额12个月后代本息和为x+x（1+0.8%）2+x（1+0.8%）4+…+x（1+0.8%）10=x［1-（1.0082）6］÷（1-1.0082），所 以x［1-（1.0082）6］÷（1-1.0082）=5000×1.00812x=5000×1.00812×（1.0082-1）÷（1-1.00812）≈880.8（元），另外还可以理解为每次付款后冲掉部分应付款及相应利息.

（2）设每次还x元，每次还款后欠款所组成的数列为｛an｝.a1=5000（1+0.8%）2-x，a2=a1（1+0.8%）2-x=5000（1+0.8%）4-x（1+0.8%）2-x，…，a6=a5（1+0.8%）12-x=5000（1+0.8%）12-x（1+0.8%）10-x（1+0.8%）8-…-x，显然a6=0，即x（1+1.0082+1.0084+…+1.00810）=5000（1+0.8%）12，又是回到（1）的情况，因此（2）的思路与（1）殊途同归.至于分3次和12次还清则可同理而得，不做累述.

说明：模型的建立是依赖脑海中的数学知识，分期付款并不是想象中那么复杂，按照银行实际复利的计算方式，运用每一次还款总和或还款总数递减方式都可以建立等比数列求和的关系式，这是抽象数学问题本质的、建立建模素养的核心，值得注意的是，对于总价和用户每月偿还的账务，都需要按照利息计算，这是体现公平的表现，实际问题中需要注意.

二、数学问题中培养模型思想

综合性数学问题中涉及的知识是多方面的，有些问题需要从另一知识的角度去思考、去建立模型.这种数学问题往往以综合性问题居多，如何从综合性问题中获得某一知识建立的模型，是教学需要关注的.

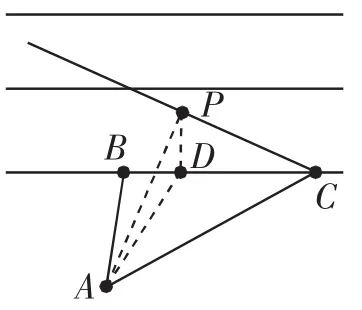
图2

问题2：如图2，某人在垂直水平地面ABC的墙面前的点A处进行射击训练，已知点A到墙面的距离为AB，某目标点P沿墙面的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小，若AB=15m，AC=25m，∠BCM=30°，则仰角的正切值最大为__________.

思考：本题是空间几何背景的问题，要计算仰角最大值，必须弄清楚两个方面：第一是仰角的基本概念，这是解三角形中的基本知识；第二是空间几何问题的处理模型是什么？不难发现，模型的建立是依赖三角形为载体，将空间几何问题渐渐处理为平面几何问题，利用问题转换的视角去解决.

说明：数学综合性问题的建模与实际问题建模有所不同，更多的角度是围绕数学某一知识建立问题的结构模型，本题以解三角形中的函数动态问题建立模型，将空间几何问题转化为平面几何中的三角形边与边之间的关系，是函数模型动态问题的典型.

三、代数化建模的重视

几何问题代数化是中学数学教学的重点之一.从近期已故数学大师吴文俊先生的话来说，数学必将朝着机械化、代数化的方向不断前进，很多理论中的几何问题都可以通过计算机进行代数化论证得以实现.中学数学中用代数的方式研究、建立数学问题的模型，成为培养解决问题的一种通式.如：用平面向量解决平面几何问题、用代数方法解决圆锥曲线问题、用空间向量解决立体几何问题等，这都需要完善的模型建立，这种模型的建立往往依赖于坐标系，让大量的代数运算成为可能.

问题3：如图3，在四棱锥PABCD中，底面ABCD是平行四边形，PA⊥AB，点C在面PAB上的射影O恰在棱AB上，直线BC与面PAB所成的角为θ.

图3

（1）求证：PA⊥平面ABCD；

思考：只针对第（2）问思考模型的建立.观察本题不难发现，要求解二面角可以从建立坐标系模型的视角出发.请学生思考建立模型的可能性，如图4～图7.

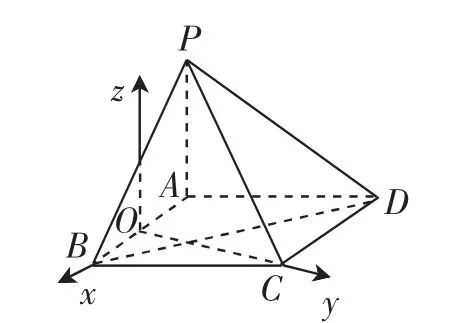
图4

图5

图6

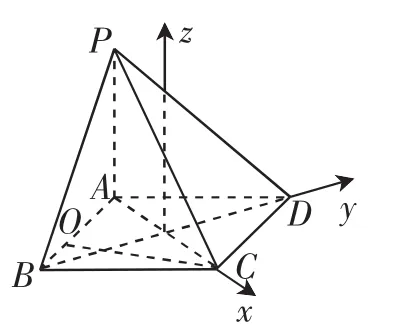
图7

从学生给出的模型建立角度来看，说明学生已经掌握了建立坐标系模型的基本素养，即尽可能多的点落在坐标系上为准则，让后续坐标的运算获得了更为简洁的方式.细致分析学生的四种图形：图4模型的建立是运算最为方便的，图5与图4基本一致；图6的建系运算是难度较大的；图7考虑到底面是菱形的缘故，因此模型的建立也是较为方便的.代数化的方式让几何的解决获得了简洁性，成为建模素养一个全新的视角和途径.

四、特殊化构造建模的培养

数学问题还需要学会特殊化的构造建模，即将抽象问题进行合理的一般化构造，形成可以求解的问题.这种建模就是构造类问题的体现，学生对于构造类建模的想法是比较缺失的.

问题4：已知函数f（x）的导函数为f′（x），若2f′（x）＞f（x）对任意的x∈R成立，那么3f（2ln2）与2f（2ln3）的大小关系为____________.

说明：构造类的问题模型建立，需要教师不断向学生渗透模型建立的基本思路，即积累常用模型、提高模式识别的能力，这种模式识别的模型建立往往为后续更高的建模素养打下扎实的基础.

总之，数学建模素养涉及解题的多方面，可以从实际应用问题、综合型问题、构造类问题等全方面的角度进行教学思考，将模型如何建立放在问题解决的首位，通过抽离情境的外表获取知识使用的本质是建模素养的关键，成为建模素养起步的第一步，是教师教学与新课程核心素养价值观不断靠拢的关键.

1.武瑞雪.对中学数学建模教学的探讨［J］.教学月刊，2011（12）.

2.方石.数学教学诠释思维品质［J］.数学通讯，2014（4）.

3.朱永祥.再谈数学复习教学的挖掘和运用［J］.中学数学，2012（2）.

4.罗先礼.数学教学的实践与思考［J］.中小学数学（高中版），2008（12）.

*本文系海门市教育科学规划微课题“核心素养下数学抽象能力的培养”的理论研究成果.