夯实基础 突出选拔 凸显创新——2017年重庆市普通高考数学试卷（全国Ⅱ卷）简析

☉重庆市教育科学研究院 张晓斌

☉重庆市涪陵区第五中学校 艾 嵩

夯实基础 突出选拔 凸显创新
——2017年重庆市普通高考数学试卷（全国Ⅱ卷）简析

☉重庆市教育科学研究院 张晓斌

☉重庆市涪陵区第五中学校 艾 嵩

一、试卷的主要参数

表1：知识点分布表

表2：文理科试题比较

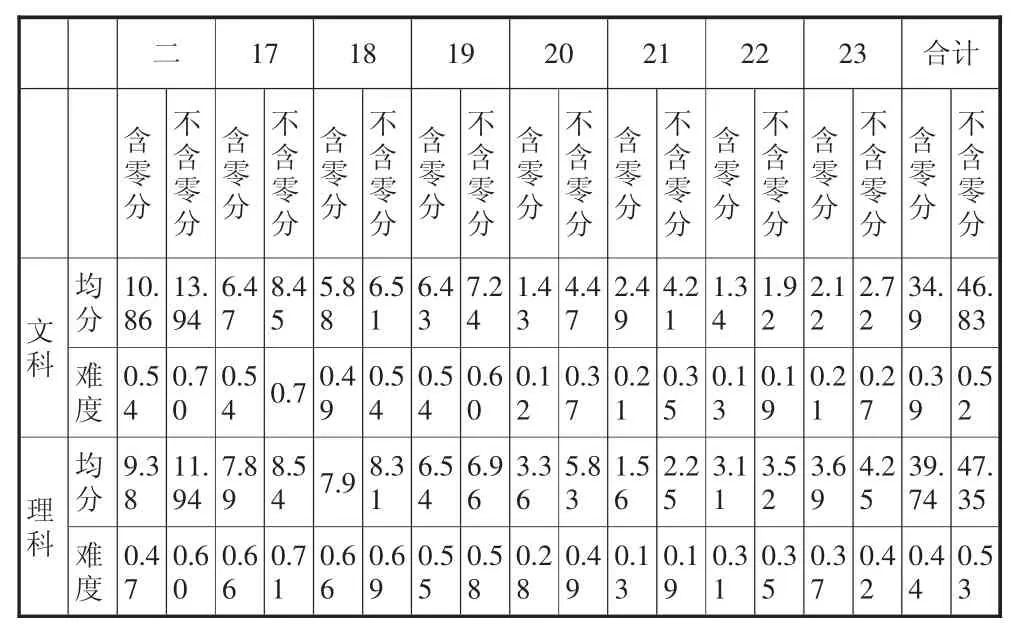
表3：填空题与解答题成绩分布表

二、试卷的主要特点

2017年数学学科高考全国Ⅱ卷以立德树人，服务高校人才选拔，导向中学数学教学为命题出发点，加强对理性思维的考查，渗透数学文化，突出对创新应用能力的考查.试卷结构稳中有变，文、理科试卷均减少了平面几何选讲的选考题，由原来的三选一变为二选一.试题关注社会发展，引导考生运用所学数学知识解决生活实际问题，富有时代气息.试卷遵循考试大纲的各项规定，各种难度的试题比例适当，有较好的区分度.试题坚持能力立意，坚持多角度、多层次地考查考生的数学素养，突出对逻辑推理、数学运算、创新意识与中国传统数学文化的考查，突出数学的基础性和应用性.试卷有利于科学选拔人才，有利于深化课程改革，有利于促进社会公平，对培养学生的创新精神、实践能力，提升学生核心素养的数学课程、教学改革有积极的导向作用.

1.加强理性思维考查，突出选拔性

2017年修订后的数学学科考试大纲削枝强干，加强主体内容，强调理性思维.2017年高考充分发挥数学思维学科的特点，加强理性思维的考查，把考查逻辑推理能力作为命题的首要任务，运用数学知识作为载体，考查考生缜密思维、严格推理能力.命题时采取分步设问、梯次递进的方式，设计不同层次的试题，区分不同能力水平的考生.创新题目设计，运用日常生活语言和情境考查逻辑推理能力，对考生逻辑推理能力的考查更加真实、有效.如第20题第（1）问以椭圆的标准方程为依托，设计了线段之间的向量关系式等条件，考查求动点轨迹的方法；第（2）问设计了动直线相互垂直的证明问题，重点考查思维的灵活性和综合应用知识解决问题的能力.

2.弘扬优秀传统文化，体现基础性

2017年修订的数学考试大纲和考试说明提出了加强数学文化考查的要求.2017年数学试卷通过数学史展示数学文化的民族性与世界性，第3题考查等比数列，试题从我国古代数学名著《算法统宗》引入，然后通过诗歌提出数学问题，阐明试题的数学史背景，试卷注重渗透中国经典数学文化，激发考生对中华民族优秀传统文化的喜爱，使考生感受到我国古代数学的成就和特点，有利于引导学生了解中国数学文化，激发爱国热情.

3.加强应用能力考查，增强实践性

2017年数学学科高考贯彻高考内容改革的要求，加强应用性，紧密结合社会实际，以考生现实生活的问题为背景设置试题，要求考生应用数学原理和数学工具解决实际问题.体现了数学在解决实际问题中的巨大作用和应用价值，体现了高考改革中加强应用性、实践性的特点.2017年数学试卷采用大题、小题结合的方式，全面、深入考查应用能力.如第19题以现实社会生产实践中，水产品养殖方法的创新问题为背景，设计了根据样本数据分析比较新、旧养殖方法产量的问题.试题的第一问设计为根据直方图估计某事件的概率，第二问设计为根据整理的数据进行随机变量间独立性的检验，第三问设计为根据直方图，估计总体中位数.本题很好地考查概率与统计的思想和方法，反映了当前全民创业、大众创新的现实，体现了“立德树人”的教育理念.2017年的数学应用题情景丰富，贴近考生，贴近生活，具有浓厚的时代气息，体现了数学与社会的密切联系，对考生的阅读理解能力、推理论证能力，理性思维进行了全方位的考查.

4.考查数学思想方法，凸显创新性

2017年试卷加强基础性和创新性，以数学基础知识、基本能力、基本思想方法为考查重点，注重对数学通性通法的考查.考查时从学科整体意义和思想价值的高度立意，淡化特殊技巧，加强针对性，有效地检测考生对数学知识中所蕴含的数学思想方法的掌握程度.理科第11、15题考查了函数与方程的思想，理科第12题考查了化归与转化的数学思想，理科第5、9、16、20题考查了数形结合的思想，理科第21题考查了分类与整合的思想，理科第13题考查了统计与概率的思想.文科第10题、理科第8题程序框图，反映了课标新增内容的程序化思想；还有理科第4题、文科第6题由三视图计算一个几何体的体积，考查几何直观能力，理科第7题、文科第9题考查了归纳推理与类比推理等.高考数学一道试题往往考查多种能力、多种思想方法，对考生的创新能力提出了要求.同时，高考试题在命制时充分考虑到考生数学能力的个体差异，绝大多数试题的解答方法、思维方式不唯一，而是多种多样.例如理科第16题，可以从抛物线的几何性质入手，还可以应用解析几何的解析法通过计算切入，一题多解，给考生提供了较大的发挥空间.这样通过方法的选择、所用解题时间的长短，甄别出考生能力的差异，达到精确区分考生的目的.

5.文理试卷层次分明，区分差异性

从表2中可以看出文理不同题达69分，相同题42分，姊妹题39分，注重区分文理科学生数学水平差异，让文理考生都考出理想水平.由于理科内容分布较广，其中尤以立体几何差异最为明显，理科对数学素养及思想方法要求更高一些.但今年文理科趋同题较多，且解答题20题文理科完全一样，所以今年文科整体难度略高于理科.

6.着力要求运算能力，突出数式性

今年试题的突出特点是普遍数式运算量较大.除大部分选择、填空题都需要进行计算外，多数解答题的运算量也很大，如理科第18题的数值计算及理科第19题立体几何的计算，文理科第20题解析几何、第21题导数等都包含复杂的数值和字符运算或论证化简.计算能力不强的考生，可能知道题目如何解，但受制于数式运算不强而无法完成.从考生实际答卷情况来看，文理科试卷的后两个题（第20、21题）普遍得分很低，除这些试题自身难度较大以外，与整张试卷的运算量大也有密切关系.

7.合理摆放试题顺序，注意合理性

从考生答题情况可以看出，个别试题的排列顺序不太合理，如理科第7题可以靠后在第10题或第11题的位置；又如文科第19题、理科第18题的答题卷中可以设计出2×2列联表，让学生节约列表格的时间.

总之，2017年数学试卷体现了考试内容的基础性、综合性、应用性和创新性，试题坚持能力立意的命题原则，体现了对“核心素养”的考查，体现了数学的科学价值和理性价值，有利于高校选拔优秀人才，有利于引导中学数学教学.

三、部分解答题考生作答情况分析及建议

【理17】除参考解答外的部分解答：

典型错误：（1）公式记错或记混，或无论题目是否有用都写上.

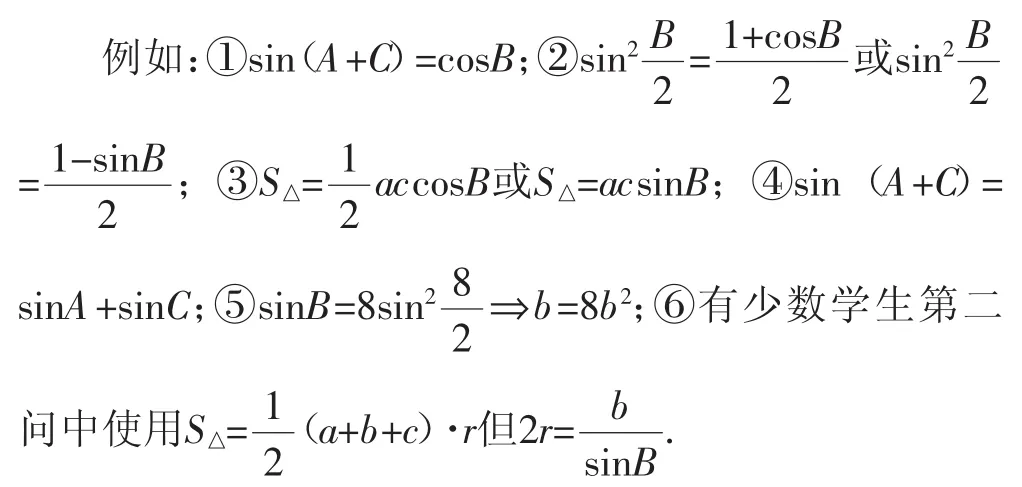
（2）计算能力不过关.

教学建议：解三角形问题是高考高频考点，命题大多放在解答题的第一题，主要利用三角形的内角和定理、正余弦定理、三角形面积公式等知识解题，解题时要灵活利用三角形的边角关系进行“边转角”、“角转边”，另外要注意a+c，ac，a2+c2三者的关系，这样的题目小而活，应加强三角恒等变形及解三角形的训练，在平时教学中注重基础知识、基本技能、基本思想方法的训练，让学生的基本能力到位.

试题评价：此题涵盖了同角三角函数的基本关系、诱导公式、降幂公式、二倍角公式、正余弦定理，全面考查了三角函数的基本知识和基本技巧，难度适中，区分度高，是选拔能力型人才的一道好题.

【文，理20】除参考解答外的部分解答：

常见错误：

③直接由两个特殊点得出轨迹方程或直接写出轨迹方程.

第（Ⅱ）问：①设θ（-3，t），P（m，n），O￣→P·P￣→Q运算出错，导致得出错误结果-3m+5n+1=0.

②设直线l方程为y=k（x+1）或y=kx+b，再代入得关于x的一元二次方程，写出韦达定理，Δ＞0等.

教学建议：本题最大问题体现在学生的运算能力弱，逻辑混乱，书写潦草，不好辨认.在教学中应加强学生运算能力，数形结合思想，函数与方程思想及化归转化思想方法的培养.让学生具备分析问题、解决问题的能力，不能一味地设计一些套路，如有的老师说遇到解析几何题就用韦达定理及判别式去求解，但在关键时候可能什么也用不上，应重视基本功的培养.

试题评价：解析几何研究的主要问题是：（1）根据已知条件，求出表示曲线的方程；（2）通过曲线的方程，研究曲线性质.本题第一问以椭圆的标准方程为依托，设计了线段之间的向量关系式等条件，考查求动点轨迹的方法；第二问设计了动直线相互垂直的证明问题，重点考查思维的灵活性和综合应用知识解决问题的能力，是一道区分度明显的好题.

【理21】除参考解答外的部分解答：

（Ⅰ）方法一：由题知（fx）=x＜ax-a-lnx（x＞0），且（fx）≥0，所以a（x-1）-lnx≥0.

当x∈（0，1）时，g（x）′＜0，g（x）递减，g（x）＜g（1）=0，所以x-1＞lnx，即＞1，所以a≤1；

当x∈（1，+∞）时，，g′（x）＞0，g（x）递增，g（x）＞g（1）=0，所以x-1＞lnx，即＜1，所以a≥1.

综上a=1.

方法二：（用洛必达法则）由题知（fx）=x（ax-a-lnx）（x＞0），且（fx）≥0，所以a（x-1）-lnx≥0.

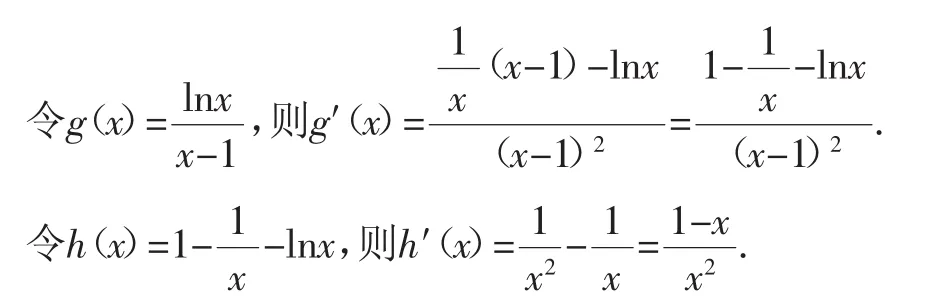
当x∈（0，1）时，h（′x）＞0，h（x）递增，h（x）＜h（1）=0，

当x∈（1，+∞）时，h（′x）＜0，h（x）递减，h（x）＜h（1）=0，所以g′（x）＜0，g（x）递减，g（x）＞=1，所以a≥1.

故a=1.

典型错误：

第一问：学生直接求导等于0，或用数形结合得到a=1，但没有进一步说明a=1可行.

②学生在证明（fx）＞e-2时取自变量x的值有很多种取法都是错的，例如f）＜0也是错的.

教学建议：作为压轴题，对学生能力要求比较高，在教学时应教会学生分析问题的能力，关键“审”准题，然后再动手处理，所以在教学中应注重逻辑思维能力的培养，规范书写，应注重通性通法教学，让考生能得到较理想的分数.

试题评价：本题主要考查函数的极值及导数的应用，结构形式简单，让学生能看清题目实质要求较高，试题“入口宽，方法多”，对函数与方程思想，化归与转化思想要求较高，能有效区分能力较强的考生，利于高校选拔优秀人才.

四、复习备考建议

1.回归基础知识，回归教材内容

重视基础知识、基本技能的复习，首轮复习时在概念定义、通性通法上回归教材，把教材上典型的例题、习题（复习题）过一下；对复习资料要处理，删去偏难、偏怪、超纲、解法太唯一的题目；对基本运算能力、空间想象能力、推理论证能力、数据处理能力等在复习时要求逐步提高，最后达到高考要求；防止出现复习的漏点、盲点（例如二项式定理、定积分、正态分布、期望、方差等）；部分降低要求或不考的内容不宜过分拓广加深（例如反函数、实际推断原理和假设检验、聚类分析等）.

2.改变教学方式，提高复习效果

突出过程教学，更要讲为什么.数学基本知识不但要理解，还要会运用，更要知道是怎么得到的，不但要讲理，更要讲道理.要注重数学基本知识的发生发展过程的教学，注重数学问题解决思路的探究过程的分析.坚持三个并重：巧算与硬算并重，主干与细节并重，重点与非重点并重.知识理解“深化”、考试题型“类化”、通性通法“强化”、解题思维“优化”.查考试说明把握方向、查高考试题明辨重点、查课标教材回归基础、查考生学习效果对症下药.让学生实现：别人“点”，心有灵犀一点通；自己“悟”，融会贯通；动手“做”，触类旁通；自主“学”，无师自通.

3.加强训练的针对性、有效性、科学性

选题既要符合学生的实际，又要符合高考的实际；训练要有“度”，不要迷信“熟能生巧”；题目不求多，要求“活、联、变”；特别注意中低档题的训练，因为它们构成了高考试卷的主体，所占分值至少有105分；“小、灵、通”题目是训练重点，抓好中低档题的三点：入手点、关键点、警戒点.

4.注重解题反思，提升思维能力

数学学习不仅是学知识，更重要的是学方法；不仅是会解题，更重要的是领悟数学思想与方法；不只知道一些数学思想与方法的名词术语，更重要的是在过程中去体会领悟出数学思想与方法.过程中就会产生思想、方法和智慧.知识教学时要展示其知识发生发展过程与探求过程，解题时要重视解题思路探求与优化，作业练习时要经常进行解题反思.一个问题解决后，就要停下来咀嚼，慢慢品味，不要急于去做第二个题，不怕慢，只怕站.引导学生反思导致解题错误的根源，反思解题思路，反思解题过程，长此以往，学生的思维能力自然会得到提升.

5.训练考试技巧，指导考试方法

教师应帮助每个学生确定自己的基本分，树立目标意识；培养学生一不怕苦、二不怕死的锲而不舍的精神；对不同高考题型处理不同：小题巧做，大题小做，难题分步做；树立良好考试心态，题易人易，我不大意；题难人难，我不畏难；综合练习后引导学生“悟一悟”，学会反思总结；注意训练书写规范，巧妙使用草稿纸，在答卷上抄写得分点的主要步骤，培养得分意识.

1.教育部考试中心.2017年普通高等学校招生全国统一考试大纲（理科）［M］.北京：高等教育出版社，2017（1）.

2.教育部考试中心.2017年普通高等学校招生全国统一考试大纲的说明（理科）［M］.北京：高等教育出版社，2017（1）.

3.张晓斌.立足重庆，促进课改——2014年高考数学重庆卷试题特点述评［J］.中学数学（上），2014（9）.

4.张晓斌，肖飞，江楠.来自高考数学阅卷场的报告——2015年重庆卷考生答题分析与教学建议［J］.中学数学（上），2015（9）.

5.张晓斌，黄亿君.突出数学核心素养，着眼学生能力发展——2016年全国数学卷（Ⅱ）试题特点分析［J］.中学数学（上），2016（8）.