让探究之花在课堂绽放——以一节“直线与圆的位置关系”复习课为例

☉江苏省清浦中学 吴洪生

让探究之花在课堂绽放
——以一节“直线与圆的位置关系”复习课为例

☉江苏省清浦中学 吴洪生

“直线方程和圆的方程”作为江苏高考的8个C级考点中的2个，是江苏高考的必考内容，也是重点考查的内容，尤以考查“直线与圆的位置关系”为主，既考小题也考大题.本节课从一道考题出发，铺展开去，引导学生重点从问题的几何属性这一视角进行探究，简化运算，快速求解.

一、试题呈现

考题 （江苏省淮阴中学2017高三4月模考第13题）如图1，已知直线y=kx+2与圆x2+y2=8交于A，B两点，M为AB的中点，C（4，4），则的最大值为_______.

二、解法探析

师：请同学们独立读题，仔细审题，认真思考，拿出解决方案.

图1

师：能具体说说第一步怎么办吗？

生1：设A（x1，y1），B（x2，y），M（x，y），由，得200，（k2+1）x2+4kx-4=0，从而有x1+x2=-=2x0，将k代入上式并化简得，+（y-1）2=1.所以动点M的轨迹方程0为x2+（y-1）2=1.

师：生1同学的解法是通过消参法，消去参数k，得到动点M的轨迹方程，其方法实质就是我们平时所讲的“设而不求”.请大家再思考，还有其他办法吗？

生2：用点差法.设A（x1，y1），B（x2，y2），M（x0，y0），则式相减得 （x1+x2）（x1-x2）+（y1+y）（y-y）=0，所以直线AB的斜率为k=212又点M在直线AB上，所以y=kx+2，从而有y=-+2，即

000有+（y0-1）2=1.所以动点M的轨迹方程为x2+（y-1）2=1.

师：同学们，解析几何主要是用代数方法研究几何问题，但它毕竞还是几何问题，能否从几何属性的视角加以考虑呢？

生3：直线y=kx+2恒过圆x2+y2=8内的定点P（0，2）.因为M为弦AB的中点，所以OM⊥AB，即OM⊥MP.由平几知识知，动点M在以OP为直径的圆Q上（设该圆圆心为Q），其方程为x2+（y-1）2=1.

师：非常好！生3同学的解法充分注意到直线与圆相交所得弦与弦心距垂直，以及圆的性质等几何属性，思路清晰，特点鲜明，方法简洁.

师：好！至此，我们同学给出了三种求动点M轨迹方程的方法，其中方法1与方法2是研究直线与圆锥曲线相交问题的常用方法，运算量相对大一些，而方法3则是借助平面图形的几何属性直接确定动点M的轨迹就是以线段OP为直径的圆，进而建立圆的方程，简洁明了.

师：下面再看看，第二步怎么办？

生5：三角代换法.因为动点M的轨迹方程为x2+（y-1）2=1，所以可设θ∈［0，2π），（cosθ-4）2+（sinθ-3）2+cos2θ+（sinθ+1）2=28-4（sinθ+2cosθ）=28-4sin（θ+φ），因此的最大值为28+4

师：对于第二步，生4，生5两位同学从不同的视角给出了两种解法，都较为简单.大家是否注意到，这里求的是两个向量模的平方和，能否用向量转化呢？

生6：如图1，设线段OC的中点为N，则有N（2，2）.又因为，两式平方相加并整理得，进而将问题转化为求|M￣→N|的最大值.

生7：其实，生6的结论也可由平几知识直接得出，运用“平行四边形两条对角线的平方和，等于它的一组邻边平方和的2倍”.

师：很好！这说明我们生7同学的平几功底是很扎实的.那现在请大家小结一下第二步的本质是什么？

生8：本质是把问题转化为我们熟悉的“圆外一定点与圆上动点之间距离的最大值”问题.运用的是化归与转化思想.当然，用三角代换法也是一个不错的选择.

师：生8同学的概括十分准确，大家给点掌声鼓励鼓励！

师：我们把两步骤联系起来看，你能发现最优解法吗？

生9：最优解法就是运用平几的性质直接归纳出动点M的轨迹是圆，再运用平几知识将所求表达式转化“圆外一定点与圆上动点之间距离的最值”.也就是说充分运用图形的几何属性，可以起到简化运算的作用.

师：生9同学说的很好！由于解析几何的本质就是用代数方法研究几何问题，因此，在解题过程中，如能恰当运用图形的几何性质，则可大大降低思维量与运算量，快速而准确地解决问题.

三、变式演练

变式练习是知识与能力之间的桥梁，是学生掌握知识、提升能力的重要抓手.学生经过一定的变式训练和深度的思维碰撞后，知识的迁移能力、运用能力将自然形成.

练习1（南师2017年高考目标测试卷1第10题）设m∈R，直线l1：x+my-2=0和直线l2：mx-y+4=0，P为直线l1与直线l2的交点，则点P到直线l：x+2y+5=0的距离的最大值为________.

师：请大家思考并给出解决办法.

生10：求出直线l1与直线l2的交点P的坐标，运用点到直线的距离公式，表示出点P到直线的距离d，再用函数思想求最大值.易求得P，当且仅当m=0时取等号，所以

师：生10同学按照题设条件，先求出交点坐标，再由点到直线的距离公式求出最值，思路正确，体现了处理此类问题的通性通法，值得肯定.但运算可不简单哟！还有没有其他的思路？

生11：挖掘题目的隐含条件，l1恒过定点A（2，0），l2恒过定点B（0，4），l1⊥l2.由此不难看出交点P在以线段AB为直径的圆C：（x-1）2+（y-2）2=5上，圆心C到直线l：x+2y+5=0的距离d′=2，直线l与圆C相离，所以圆上动点到直线l距离的最大值

师：生11同学太棒了！他的思路在于充分挖掘题目的隐含条件，一方面发现两直线分别过一定点，另一方面发现两直线互相垂直，从而说明动点P在定圆C上，进一步将问题转化为圆上动点到定直线距离的最大值问题，再利用几何属性解题，快速简单！因此，对于几何问题的探究，如能恰当运用图形的几何属性，可以精准把握题目要领，使探究活动更高效！

练习2（南师2017年高考目标测试卷4第12题）圆C：x2+y2-2x-2y+1=0，直线l：3x+4y-17=0.若在直线l上任取一点M作圆C的切线MA，MB，切点分别为A，B，则线段AB长度取最小值时直线AB的方程为_______.

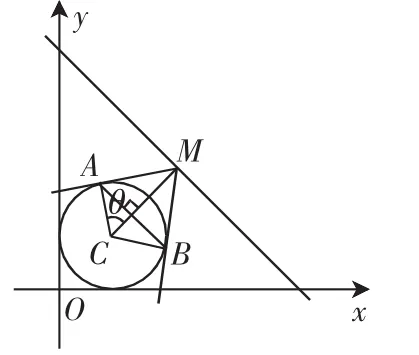
图2

师：请同学们帮我分析一下思路.

师：本题也是从图形的几何属性出发，结合三角函数将“线段AB长度最小”转化为“线段CM长度最小”，从而有CM⊥l.

练习3（2017年宿迁三模第13题）在平面直角坐标系xOy中，圆C：（x+2）2+（y-m）2=3.若圆C存在以G为中点的弦AB，且AB=2GO，则实数m的取值范围是_________.

师：本题有何特点？

分析1：如图3，设G（a，b），由AB=2GO，得AG=GO，从而3-［（a+2）2+（b+m）2］=a2+b2，整理得（a+1）2+≥0.所以m∈

图3

分析2：由AB=2GO，得OA⊥OB.过点O作圆C的两条切线OM，ON，由平几知识知，∠MON≥∠AOB=，所以sin∠CON≥sin，即OC≤，从而有m∈

练习4（2017年南京三模第13题）在平面直角坐标系xOy中，圆O：x2+y2=1，圆M：（x+a+3）2+（y-2a）2=1，其中a为实数.若圆O与圆M上分别存在点P，Q，使得∠OQP=，则实数a的取值范围是_______.

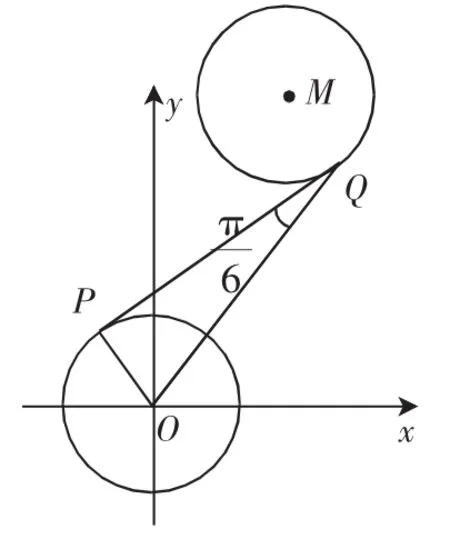
图4

四、课后检测

1.（南京市2017年高三二模数学卷第11题）在平面直角坐标系xOy中，直线l1：kx-y+2=0和直线l2：x+ky-2=0相交于点P，则当实数k变化时，点P到直线x-y-4=0的距离的最大值为_________.

2.在平直角坐标系xOy中，已知圆C：x2+（y-3）2=2，点A是x轴上的一个动点，AP，AQ分别切圆C于P，Q两点，则线段PQ的长的取值范围为_________.

3.在平面直角坐标系xOy中，M为圆C：（x-a）2+（y-1）2=上任意一点，N为直线l：ax+y+3=0上任意一点，若以M为圆心，MN为半径的圆与圆C至多有一个公共点，则正数a的最小值为_________.

五、教学思考

直线与圆的位置关系一直是高考考查的重点和热点，在江苏高考中的地位很重要，相关试题多在填空题中出现，属中、高档题；有时也会设计直线与圆的解答题.结合本节课内容，有如下教学思考：

1.明确《课标》与《考试说明》要求

《高中数学课程标准（实验）》明确指出：在平面直角坐标系中，结合具体图形，探索确定直线位置的几何要素；回顾确定圆的几何要素，在平面直角坐标系中，探索并掌握圆的标准方程和一般方程；能用直线和圆的方程解决一些简单的问题.《考试说明》要求：能根据两条直线的斜率判定这两条直线平行或垂直；会求两直线的交点坐标；掌握圆的标准方程和一般方程；能判断直线与圆、圆与圆的位置关系.

2.重视直线与圆的几何性质与代数表示之间的关系

直线与圆的位置关系体现了圆的几何性质和代数方法的结合，“代数法”与“几何法”是从不同的方面和思路来判断的，“代数法”侧重于“数”，更多倾向于“坐标”与“方程”；而“几何法”则侧重于“形”，利用了图形的性质.有些直线与圆的问题，其条件往往联系着某种明确的几何性质，如果将这种几何性质蕴含的数量关系转化为代数表示，就可以简化代数运算.

3.圆的几何性质不容忽视

学生在初中已对直线与圆的性质进行了初步的学习，因此，在解答直线与圆的有关问题时，理应先从几何的角度思考解题的方法与途径.然而，在教学过程中能明显感受到学生对圆的几何性质的掌握程度不高，且探究比较少，在解答与圆有关的问题时，出手常偏重代数运算，忽视几何性质，导致简单问题复杂化.因此，我们在平时的教学过程中，要有意识地带领学生学习、巩固、探究直线与圆的有关性质，努力将几何性质与代数方法有机地结合起来，简化运算过程，实现快速解答.

4.注重数学思想

数学思想是数学知识的灵魂，是解决数学问题的方法与策略，学生对数学思想的把握程度，体现学生数学素养的高度，决定学生在问题解决过程中的策略水平.通过高考试题的研究可以发现，关于直线与圆的方程的试题，常常突出考查数形结合、分类讨论、函数与方程、化归与转化等数学思想.