无刷直流电机变论域模糊PID控制系统的研究与仿真

李 艳， 李可可， 张孝杰

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021; 2.陕西省农产品加工技术研究院， 陕西 西安 710021； 3.濮阳市自来水公司生产科， 河南 濮阳 451000)

无刷直流电机变论域模糊PID控制系统的研究与仿真

李 艳1,2， 李可可1， 张孝杰3

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021; 2.陕西省农产品加工技术研究院， 陕西 西安 710021； 3.濮阳市自来水公司生产科， 河南 濮阳 451000)

为了改善无刷直流电机的调速性能，针对常规PID在直流电机应用上存在响应速度慢、稳定性差等缺陷，研究了一种基于变论域思想的模糊PID控制方案.设计了一种二阶模糊控制器，该控制器根据系统的控制需求实时调整伸缩因子，第一阶模糊控制器利用伸缩因子改变第二阶模糊控制器的论域，从而能够根据直流电机的速度变化进行论域的伸缩变化.经过MATLAB仿真，结果表明：变论域自适应模糊PID控制直流电机时相对于PID控制和模糊PID控制具有无超调、响应速度快和良好的鲁棒性能的优点.

变论域； 模糊PID； 直流电机； 调速

Abstract:In order to improve the performance of brushless DC motor,for conventional PID in DC motor applications defects slow response speed, poor stability,the paper research a kind of fuzzy PID control scheme based on ideas and variable region, a second order fuzzy controller was designed,the controller according to the control requirement of system real time adjust the scaling factor,the first order fuzzy controller changes the domain of the second order fuzzy controller by using the dilation factor,thus,the expansion of the field can be carried out according to the change of the speed of the DC motor.Through MATLAB simulation,The results show that the adaptive fuzzy PID control and variable region DC machine compared with PID control and fuzzy PID control has no overshoot,quick response speed and good robust performance.

Keywords:variable universe; fuzzy PID; DC motor; control of motor speed

0 引言

随着电力电子和永磁材料的快速发展，无刷直流电机在各行各业中的应用得到迅速推广，因此人们对直流电机的鲁棒性和快速性提出了较高的要求.直流电机速度控制大多采用传统PID控制方案[1,2]，PID控制方案具有原理简单、稳定性好等优点.但是由于无刷直流电机调速系统具有一定的非线性，传统的PID控制会出现响应速度慢、稳定性差等缺点，为了提高直流电机的调速性能,智能控制受到越来越多的关注.于是近年来自适应模糊PID控制方案被用来提高直流电机的调速性能[3]，相比传统PID控制效果有了明显的提升，基本上解决了常规控制的控制精度问题，但是基于模糊规则设计的模糊控制器是基于专家经验的一种非线性控制器，模糊控制缺乏准确的隶属度函数和调整方法，隶属度函数和控制规则一旦设定确定，在系统的调节过程中就不能任意改动，针对直流电机这种时变、非线性系统[4]，模糊控制规则只是在调节刚开始的过渡过程中起作用，而且误差较小时PID参数往往不易调节，因而模糊PID控制的自适应能力有限.

为了解决上述问题，本文在自适应模糊PID控制方案基础上，引入了变论域的思想，形成一种可变论域的有自适应能力的模糊PID控制策略，即变论域模糊PID控制策略[5-6].通过论域调整改善模糊PID控制器参数调整精度和范围，实现论域随着系统的控制需求进行响应的伸缩，使得初始设置的规则变为适应系统随时变化的规则，根据误差不断的调整，使得该控制方案在直流电机调速的应用上具有比自适应模糊PID控制具有更好的自适应能力、稳定性.目前，变论域模糊控制器设计常用的方法是选择合适的论域伸缩因子实现变论域[7]，但是伸缩因子的函数形式与函数中的参数选择较为繁琐，且函数形式选择的合理性与系统控制性能密切相关，为了克服这些不足，本文设计了二阶模糊控制器并把变论域二阶模糊控制器应用在无刷直流电机的速度控制上[8,9]，对常规PID、模糊PID和变论域模糊PID控制方案在MATLAB环境下进行仿真比较，结果显示本文设计的变论域模糊PID控制方案在直流电机的速度调节上具有较好的响应速度、稳定性.

1 直流电机数学模型

直流电机驱动系统如图1所示[10,11].在分析过程中，为了方便，假设磁路不饱和，不计算涡流和磁滞损耗.

图1 直流电机驱动系统图

在额定励磁条件下，直流电机电压平衡关系式为：

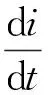
(1)

式(1)中：R和L分别为电机的电枢绕组和电枢电感，U为电枢电压，i为电流，e为电机电枢反电势，e=keω，ω为电机的角速度，ke为反电动势常数.

力矩平衡关系式为：

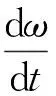
(2)

式(2)中：J为转动惯量，Tl为总负载转矩，Te为电磁转矩，且Te=kli，kl为电磁转矩系数，B为粘性阻尼系数.

两式联立可以得到式子为：

(3)

通过拉氏变换可得到传递函数为：

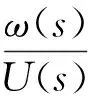
(4)

2 模糊PID原理

常规PID的思想是根据设定输入与实际输出的偏差，按比例、积分和微分的函数关系进行计算.在直流电机控制中，常用的是增量式PID，其原理式为：

ΔU(k)=KPΔe(k)+KPe(k)+KD[Δe(k)-

Δe(k-1)]

(5)

其中,KP为比例系数，KI为积分函数，KD为微分函数.

模糊PID控制是利用模糊规则，根据偏差e和偏差变化率ec的大小实时在线地调整PID的三个参数KP、KI和KD，以达到使整个系统具有良好的动静态性能的目的，其控制系统结构图如图2所示.

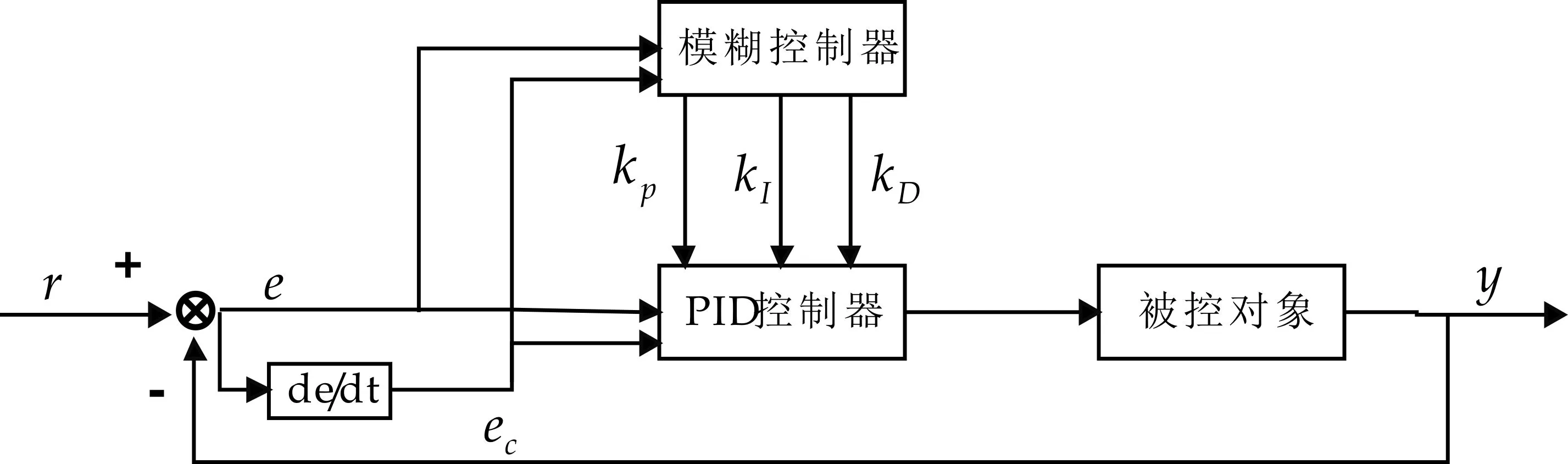
图2 模糊PID控制系统结构框图

在模糊PID控制中，模糊控制器一旦确定，其结构就不能随意改动，因而适应能力就降低了，当模糊控制器的论域范围过小时，容易造成输入量超出范围，导致控制器失控；当论域范围过大时，控制器不能使用所有的规则，同样不能使模糊控制器发挥应有的效能.

3 变论域模糊PID原理

变论域的思想是在模糊控制规则不变的前提下，变量的模糊论域在初始范围的基础上，根据误差及误差变化率的变化进行相应的伸缩变化，当误差增大时论域扩展；当误差变小时论域压缩，相当于局部增加了控制规则，从而提高控制精度.

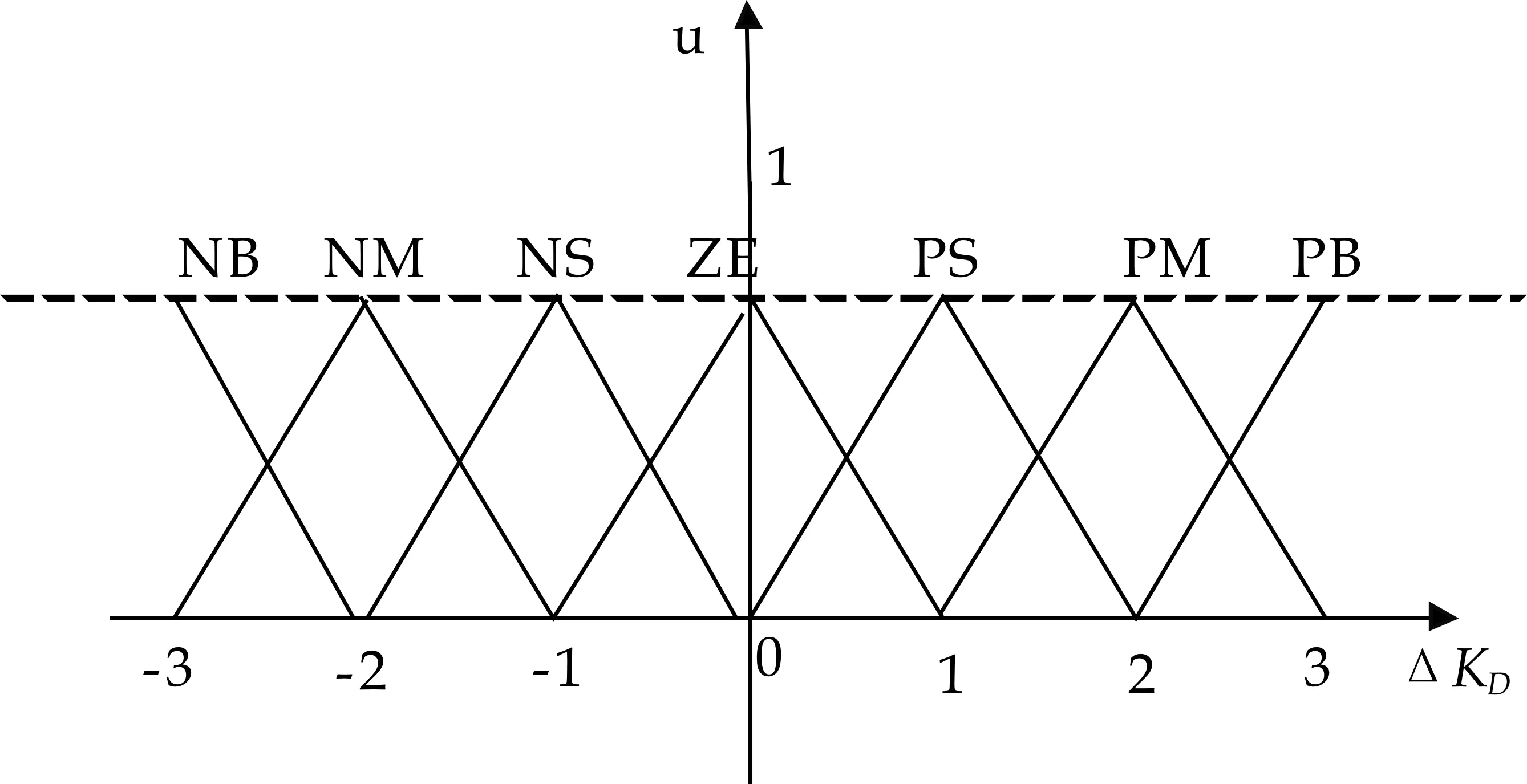
图3 论域变化情况图

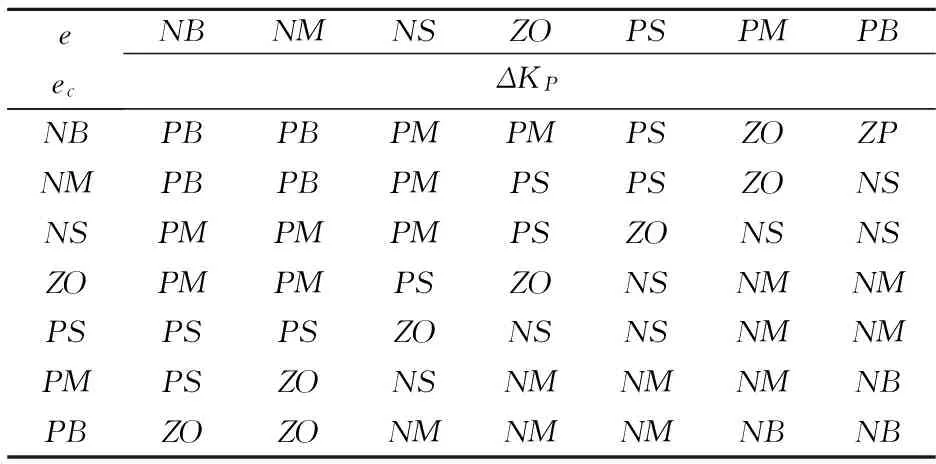
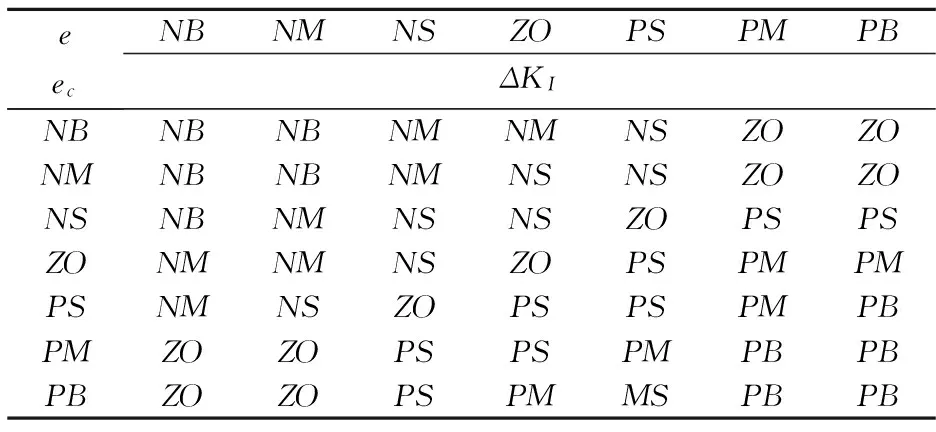
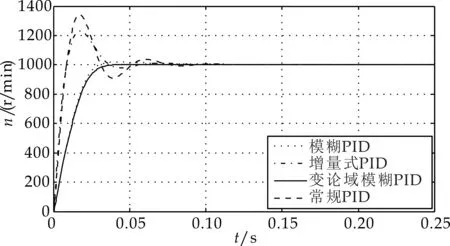
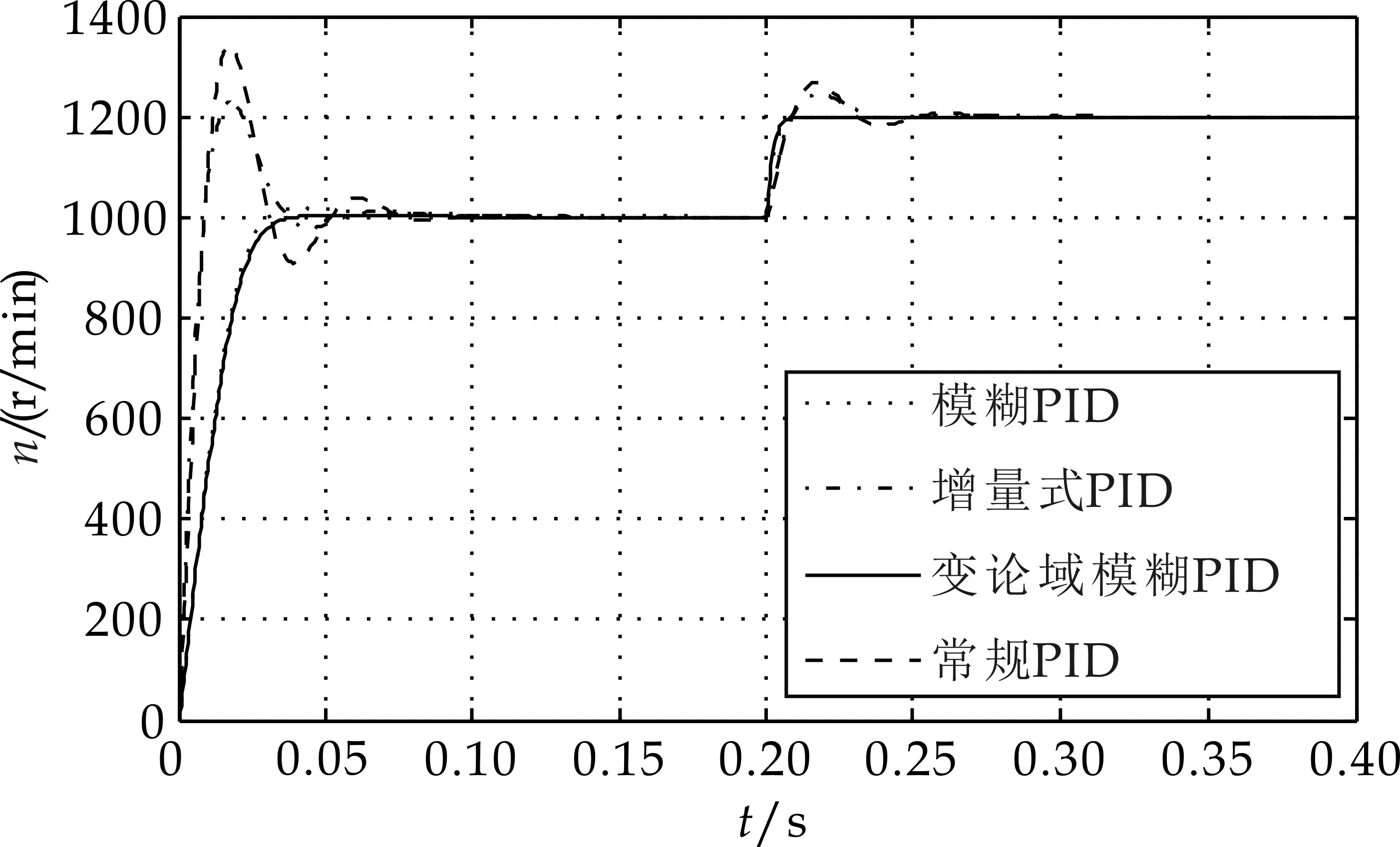
假设一个双输入单输出的模糊控制系统的输入变量为e、ec，输出变量为y，论域分别为X1=[-EE]，X2=[-ECEC]，Y=[-UU]，A={Ai}、B={Bi}和C={Ci}(1≤i≤n,其中i是整数，表示为模糊控制规则数)分别为论域X1、X2和Y以基元组为基础的模糊划分[12]，ei、eci、yi分别表示Ai、Bi、Ci的峰点，其中-E

ei(k)=α[e(k)]ei(0)

(6)

eci(k)=α[ec(k)]eci(0)

(7)

y(k+1)=Y[e(k),ec(k),k]=

(8)

由上式可以推导出变论域模糊控制的离散表达式为：

y(k+1)=γ[y(k)]·

Y{e(k)/α[e(k)],ec(k)/β[ec(k)]}=

Bi{ec(k)/β[e(k)]}·yi(0)

(9)

由此可以看出基于变论域的模糊控制是一种自适应的模糊控制，这种自适应的模糊控制是以论域的变化应以误差的变化，此时的控制器降低了对隶属函数的形状以及模糊控制规则和论域的依赖，简化了模糊控制器的设计，只需要掌握控制系统大致的变化方向，形成一组控制规则就可以.变论域模糊PID控制就是利用变论域理论与模糊PID控制原理相结合，通过变论域自适应律的调整改善模糊PID的参数调整精度和范围，则可以克服常规模糊PID控制自适应能力有限的缺点，这种模糊控制器能实时跟踪控制系统的动态变化，提高系统的自适应能力.

4 变论域模糊PID控制器设计与仿真

4.1 变论域模糊PID控制器设计

变论域模糊PID控制器实质就是在常规模糊PID的基础上增加了伸缩因子，通过伸缩因子改变论域的大小进而对模糊PID参数进行调整，一般用基于函数模型的伸缩因子来控制论域的范围，所以伸缩因子的选择直接决定了变论域模糊PID控制器的性能，伸缩因子选择的合适与否对控制效果有着较大影响，而且函数中的参数的选择较为繁琐，因此本设计中的变论域模糊 PID控制器选择双模糊控制器，其控制器的控制系统结构框图如图4所示.

图4 变论域模糊PID控制系统结构框图

其控制过程为：模糊控制器1通过控制对象的反馈值与设定值的偏差和其变化率进行论域调整，得到伸缩因子λ(0<λ<1)，然后通过伸缩因子作用在模糊控制器2上，实时在线的改变模糊控制器2的论域大小，最后通过PID控制对参数KP、KI和KD进行在线调整，从而系统获得更好的控制效果[14,15].

4.1.1 模糊控制器1的设计

选择直流电机转速的偏差e和偏差变化率ec作为模糊控制器1的输入量，伸缩因子λ作为输出，模糊子集均为：B、M、S,分别代表大、中、小，输入量论域都为[0 6]，各语言值均选择三角形的隶属度函数，模糊控制器1的隶属度函数曲线为图5所示.

图5 隶属度函数曲线图

因为伸缩因子需要输入量相对较大时使模糊控制器2的论域变大，在输入量较小时使模糊控制器2的论域变小，所以模糊控制规则设计如表1所示.

表1 λ模糊控制规则

4.1.2 模糊控制器2的设计

模糊控制器2选择其偏差e和偏差变化率ec作为输入量，模糊语言变量分别为E和EC，输出量分别为PID的参数的修正值ΔKP、ΔKI和ΔKD，其相应的模糊语言变量分别为KP、KI和KD，模糊子集均为：NB、NM、NS、ZO、PS、PM和PB，分别代表负大、负中、负小、零、正小、正中和正大，PID参数的模糊校正控制表如表2～4所示.

表2 ΔKP模糊控制规则表

表3 ΔKD模糊控制规则

表4 ΔKI模糊控制规则

此系统的输入为e、ec，输出为KP、KI和KD，e和ec的量化论域值均为[-3 3],修正值ΔKP、ΔKI和ΔKD的量化论域值分别为[-0.3 0.3]、[-0.06 0.06]和[-3 3]，各语言值均选择三角形的隶属度函数，如图6～8所示.

其中，变论域模糊PID的结构与模糊PID的结构在模糊PID部分是相同的，只是在模糊PID控制器前面增加了一个模糊控制器，实现了模糊变论域的实时调整，模糊PID的参数调整算式为：KP=KP0+ΔKP、KI=KI0+ΔKI、KD=KD0+ΔKD.KP0、KI0和KD0分别为PID的设定初始值，ΔKP、ΔKI、ΔKD分别为模糊PID控制器的输出，也就是PID参数的调整值，得到的KP、KI和KD经过模糊推理和去模糊化最后得到系统的输出，即为式子：

图6 ΔKp隶属度函数

图8 ΔKD隶属度函数

4.2 系统仿真

在Simulink环境下，建立基于变论域模糊PID控制器的无刷直流电机调速系统仿真模型[16]，建立的变论域模糊PID控制系统结构框图如图9所示.分别对常规PID、增量式PID、模糊PID和变论域模糊PID进行仿真，并进行比较.

图9 变论域模糊PID控制器仿真图

无刷直流电机给定转速n=1 000 (r/min)情况下，图10位电机转速在常规PID、增量式PID、模糊PID和变论域模糊PID在MATLAB仿真平台下的仿真图，其中常规PID的参数kp=6，ki=0.15，kd=0.01，增量式PID的参kp=6，ki=0.12，kd=0.01.从图10可以看出，PID控制和增量式PID控制的超调量较大，分别为σ1%=33.3、σ2%=24，调节时间ts1=0.08 s，上升时间tr1=0.01 s，模糊PID控制的超调量为σ3%=1.3且调节时间ts2=0.06 s，变论域模糊PID控制的效果优于PID控制和模糊PID控制，调节时间较小，时间为ts3=0.04 s，且基本没有超调，具有更快的响应速度.

图10 直流电机转速比较图

图11是在0.2 s时系统负载突然改变的仿真图，通过仿真图可以看出PID控制和增量式PID控制在负载改变的情况下，PID控制出现较大的震荡，增量式PID也出现震荡，但优于常规PID控制，其中模糊PID控制和变论域模糊PID控制由于具有较强的自适应能力，在负载改变时能够较快的恢复，具有良好的抗干扰能力和稳态性能.

图11 负载改变下的曲线比较图

图12是在0.2 s时调整直流电机转速下的仿真图，通过仿真图可以看出PID控制和增量式PID控制在转速改变的情况下，PID控制和增量式PID响应速度慢、适应能力弱，其中模糊PID控制和变论域模糊PID控制由于具有较强的自适应能力，在转速改变的情况下能够较快的适应，具有较快的响应速度.

图12 速度改变下的曲线比较图

通过以上的分析，本文所设计的变论域模糊PID控制器对于转速的改变和外部负载的改变具有较快的响应速度，抗干扰能力强，稳定性好等特点，具有较强的自适应能力.

5 结论

在使用二阶模糊控制器的变论域模糊PID控制方法过程中，不仅对KP、KI和KD进行自适应调整，还可以对伸缩因子进行实时改变来对模糊推理的论域进行调节，使控制器具有较好的控制效果，相对于PID控制和模糊PID控制，其适应能力和抗干扰能力明显增强，响应速度加快.为今后分析该类电机性能和对其控制策略的研究提供了新的方法，具有较好的研究价值.

[1] 周 阳,周美娇,殷 戈.直流电机调速系统设计及PID参数整定[J].电子科技,2016,29(5):153-157.

[2] 张红涛,闫 林,徐晓辉,等.基于单片机PID算法的无刷直流电机控制系统的研究[J].现代电子技术,2007(10):52-54.

[3] 刘慧博,王 静,吴彦合.无刷直流电机模糊自适应PID控制研究与仿真[J].控制工程,2014,21(4):583-587.

[4] 付子义,邢 阳.无刷直流电机的变论域模糊自适应控制[J].计算机仿真,2015,32(5):336-339.

[5] 李红伟.变论域模糊控制的无刷直流电机控制系统[J].控制工程,2010,17(5):599-602.

[6] 陈兵伟,廖卫强.应用变论域模糊PID的直流电机调速系统[J].集美大学学报,2011,16(3):207-211.

[7] 谭兵文,李春文.几种变论域伸缩因子选择方法的比较[J].科学技术与工程,2013,13(4):908-911.

[8] 曹玉丽,史仪凯,袁小庆,等.自平衡机器人变论域模糊PID控制研究[J].计算机仿真,2013,30(2):347-350.

[9] 李明爱,焦利芳,焦俊飞.自平衡两轮机器人的分层模糊控制[J].控制工程,2009,16(1):80-82.

[10] 张 琛.直流无刷电动机原理与应用[M].北京:机械工业出版社,2004.

[11] 李铁才,杜坤梅.电机控制技术[M].哈尔滨：哈尔滨工业大学出版社,2000.

[12] 李洪兴.模糊控制的插值机理[J].中国科学,1998,28(3): 259-267.

[13] 裘智峰,黄 灯,桂卫平,等.基于变论域插值模糊PID控制系统的研究与应用[J].仪器仪表学报,2008,29(11):2 435-2 440.

[14] 李洪兴.Fuzzy-控制器的本质与一类高精度Fuzzy控制器的设计[J].控制理论与应用,1997,14(6):868-872.

[15] 李 震,陈 以,韩元杰.可变论域Fuzzy-PID控制器的设计与仿真[J].自动化技术与应用,2004,23(12):29-32.

[16] 刘金琨.先进PID控制MATLAB仿真[M].2版.北京：电子工业出版社,2007.

【责任编辑：蒋亚儒】

ResearchandsimulationofvariableuniversefuzzyPIDcontrolsystemforbrushlessDCmotor

LI Yan1,2， LI Ke-ke1， ZHANG Xiao-jie3

(1.College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China； 2.Shaanxi Research Institute of Agricultural Products Processing Technology， Xi′an 710021， China; 3.Production Department of Puyang Water Supply Company, Puyang 451000, China)

2017-08-28

陕西省科技厅科学技术研究发展计划项目(2013K07-28); 陕西省教育厅专项科研计划项目(14JK1094)

李 艳(1972-)，女，四川仁寿人，副教授，硕士生导师，研究方向：工业自动化与智能控制

2096-398X(2017)05-0162-06

TM33

A