船舶引航过程风险马尔科夫链模型动态仿真

胡甚平，黄常海，邓华，黄道正

(1.上海海事大学 商船学院，上海 200135; 2.江苏海事职业技术学院 航海技术系，江苏 南京 211170; 3.上海海事大学 交通运输学院， 上海 200135)

船舶引航过程风险马尔科夫链模型动态仿真

胡甚平1，黄常海1，邓华2，黄道正3

(1.上海海事大学 商船学院，上海 200135; 2.江苏海事职业技术学院 航海技术系，江苏 南京 211170; 3.上海海事大学 交通运输学院， 上海 200135)

为定量研究特定水域船舶引航过程风险演化规律，有效进行船舶进出港安全预控，本文通过对港区水域船舶引航作业工作流程分析，确立不同船舶引航作业任务的风险程度，提出船舶引航状态处于港内外锚地、航道和泊位前沿等水域之间的转移方程。计算结果表明：船舶引航状态的转移符合马氏稳态特性，经潮汐型波动后走向稳定；船舶航行状态转移的过程变量对港区水域总体船舶秩序影响明显。基于马尔科夫链蒙特卡洛方法的过程风险仿真模型适用于海上交通风险的模拟分析，可为船舶安全管理提供风险演化的基本规律。

风险评估； 风险仿真； 船舶引航； 马尔科夫链蒙特卡洛； 船舶流量； 港口交通； 马尔科夫链； 动态系统仿真

Abstract：The dynamic system simulation of effective ship embarking or disembarking at harbors is necessary to quantitatively analyze and identify risk evolution in ship pilotage in specific waters for safety control. In this study, the working process of the pilotage operation of a ship in port waters is analyzed and the risk degrees of different ship pilotage operation tasks are determined. The calculation result shows that the transfer of pilotage state complies with Markov steady- state characteristics and remains stable after tide- type fluctuations. In addition, the transferring variable remarkably affects the whole ship flow in the harbor. The dynamic system simulation model with the Markov Chain Monte Carlo algorithm is suitable for the risk analysis of maritime traffic risk and can provide the basic law for the evolution of risk in the safety management of marine traffic.

Keywords： risk assessment; risk simulation; ship pilotage; Markov Chain Monte Carlo; ship flow; harbour traffic; Markov Chain; dynamic system simulation

随着航运业的发展，大量的船舶频繁活跃于港口水域，使港口水域通航密度大大增加，交通环境更加复杂，导致船舶水上交通风险逐渐增加[1]。目前，国内进出港口船舶中有50%左右的船舶是在引航员的引领下完成的，部分对外港口甚至达到90%，船舶引航是港口生产和快速发展中不可替代的环节，保证了港区的安全和水域的清洁，提升了港口综合服务能力[2]。船舶引航在保障地方经济发展、港口生产能力和港口水域交通安全方面的作用不可替代[3]。

目前，国内外已有很多学者采用定性、定量以及定性定量相结合的方法从不同角度研究港区水域船舶航行风险问题。方泉根等采用综合安全评估方法对船舶引航风险形成原因进行分析[3-4]。方诚等引入贝叶斯理论对船舶引航风险分别提出预测模型和动态网络推理模型[5]。Cameron提出引航安全决策研究[6]。马飞等提出船舶引航中的风险脆弱性量化问题[7]。Wu等引入模糊综合评判法对引航系统进行评价[8]。Görçün等采用综合安全评估方法对海峡水域船舶航行风险进行量化研究[9]。Pak等采用模糊层次分析法对港口水域船舶安全航行风险进行量化研究[10]。Praetorius等提出如何适应不断变化的操作条件的船舶交通系统(vessel traffic system,VTS)操作人员适应力模型[11]。这些文献在船舶引航静态风险量化方面取得进展，然而对于时序下的船舶引航动态风险研究有待深入。

量化随机过程下的船舶港区航行风险是进行大数据条件下风险预防和控制的基础问题。胡甚平等提出基于人工智能云模型的蒙特卡洛方法研究风险耦合机理[12]。Faghih Roohi引入马尔科夫链蒙特卡洛方法(Markov chain Monte Carlo，MCMC)对海上交通风险进行动态仿真，通过船舶交通事件、事故与严重事故之间的风险转移的动态系统仿真得出风险系统动态演化规律，分析安全风险的分布以及现有交通条件下的发展趋势[13]。动态风险纳入随机过程研究是一种新尝试。

本文通过港区水域船舶引航作业工作流程分析，确立船舶引航状态处于港内外锚地、航道和泊位前沿等水域之间的状态转移方程。采用马尔科夫链蒙特卡洛方法，提出港区水域船舶引航风险动态系统仿真模型。结合港区水域船舶引航状态转移矩阵，进行马尔科夫链蒙特卡洛仿真实验与分析。

1 问题的描述

1．1 船舶引航过程风险分析

引航是指在一定的水域内，由专门性的从业人员登上船舶，并就船舶驶抵目的地的有关问题，向船长提出有关航行问题的建议，或者在不解除船长对于全船驾驶责任的情况下，把船舶安全地从锚地或泊位引进、带出港口或在港内移泊。因此，引航任务是由作业属性和初始船舶状态组成，作业属性包括进出港或移泊，初始船舶状态包括内外锚地或泊位。引航过程则是由引航任务的设定、人员与船舶内部因素相关联或相互作用的活动以及预期的船舶安全营运的状态等组成，即船舶通过进出港航行(含调头)、靠离泊(含抛起锚、系离浮等)和移泊等，最终实现锚地与泊位之间的空间状态转移。船舶引航作业是船舶在不同区域间进行状态转移，从而完成进出港航行、靠离泊和移泊作业任务(见表1)。

表1 船舶引航作业流程

在港区水域，船舶引航过程需通过港外锚地、港内锚地、港区航道和泊位(含前沿水域等附近水域)等改变而完成。鉴于船舶引航作业是船舶在状态转移过程中完成进出港航行、靠离泊和移泊任务，船舶引航过程风险包含船舶引航中航行、靠泊、离泊、移泊等行为的风险[4]。

因而，船舶进出港口(或移泊)的风险最终表现为不同区域不同作业风险的组合。比如，进港船舶引航风险为外锚地起锚作业、航道航行作业和泊位靠泊作业等风险的组合(见图1)。

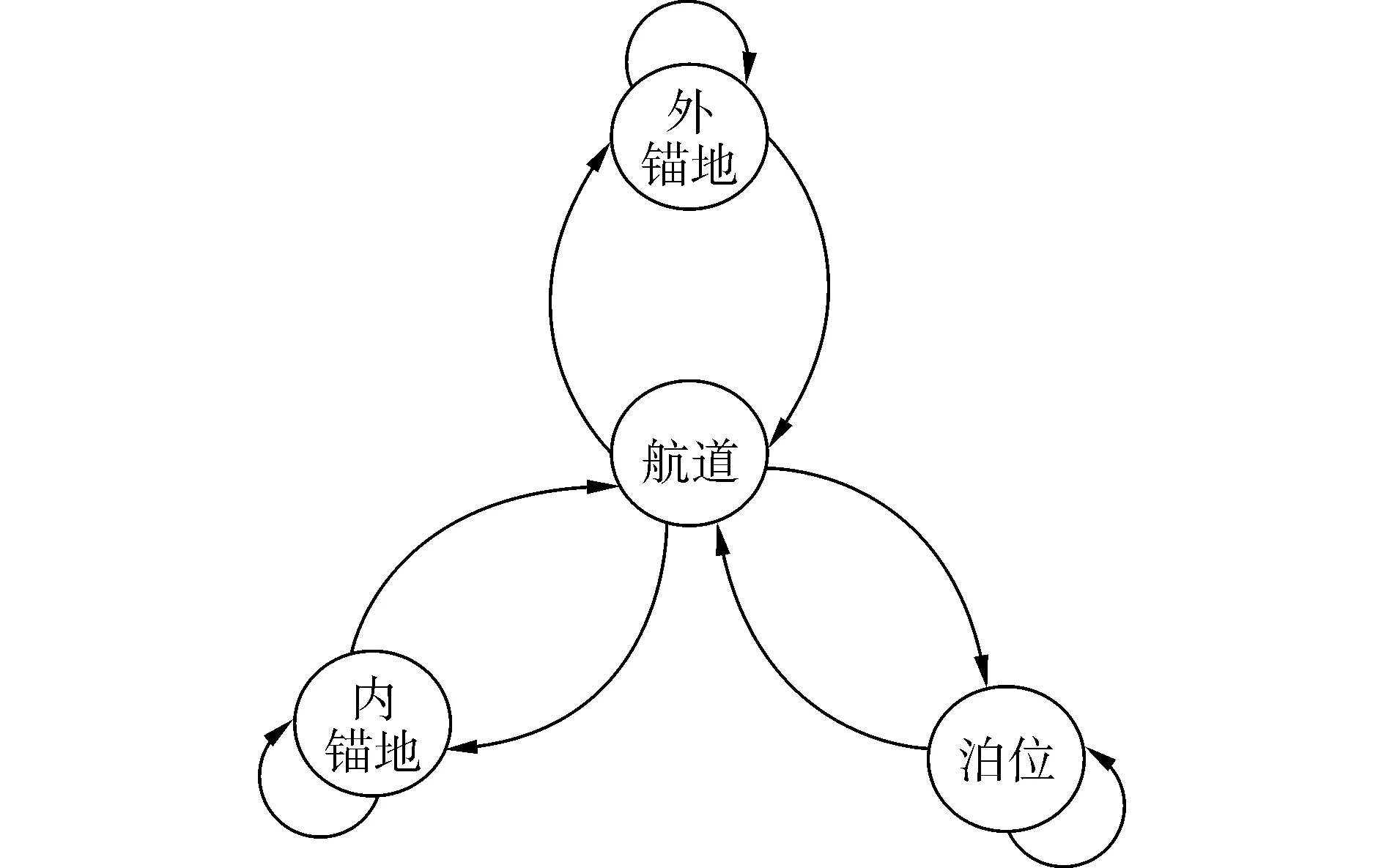
图1 船舶港区水域状态转移图Fig.1 State transition diagram on ship pilotage

1.2 船舶引航过程风险动态模型的建立

船舶引航过程动态风险可以定义为在设定的时间或过程中船舶所处随机状态下安全引航作业风险的组合，数学表达为

(1)

式中：R(t)为设定时间t下的风险值，r为船舶不同引航作业状态xi(i=1,2,3,4)非正常事件发生可能性和后果程度组合的风险值，S(t)为时间t时刻船舶暴露着的引航状态，S(0)为船舶t=0的引航初始状态，T为船舶引航状态转移变量，满足：

(2)

式中:μij为不同状态之间变化xi→xj的转移概率。

2 船舶引航过程风险的动态仿真

2.1 马尔科夫链蒙特卡洛方法

船舶引航安全系统仿真是对船舶引航过程的一种模拟，利用数学模型来模拟船舶引航安全系统发展变化的规律。MCMC作为统计计算方法，也是动态系统仿真的方法之一，通过设定随机过程，重复生成时间序列，估计分布参数和统计数值，进而研究其分布特征[14]。首先通过计算机进行静态模拟，然后将离散时间的马尔科夫链或连续时间的马尔科夫过程引入到蒙特卡洛模拟中，实现抽样分布随模拟条件进而改变的动态系统模拟。由于涉及时间序列反复生成，弥补了传统的蒙特卡洛积分只能进行静态模拟的缺陷。该方法在机器学习、人工智能等领域具有广泛的应用[15]。

MCMC用一个复杂分布进行采样，马尔科夫链存在唯一的平稳分布，使得样本点服从该复杂分布。有限状态是不可约非周期的，当转移步数趋向于无穷时，每个状态服从指定的概率分布。因此，从概率分布中进行采样，可以构造一个马尔科夫链过程，使得它的平稳分布是复杂分布[16]。

2.2 船舶引航过程风险动态系统仿真

马尔科夫链体现的是离散状态在离散时间中或连续时间转换关系，下一个状态只决定与当前的状态。就船舶引航任务而言，每一个引航任务只描述当前状态与下一个状态，下一个状态与当前状态相关。

状态图的转换关系可以用转换矩阵T来表示。考虑一般的情况，满足条件下经过一定的马尔科夫链迭代后系统分布会趋近一个稳定分布，即最后的μ(t)服从目标分布S(x)(t)采样。在采用 MCMC方法时，马尔科夫链转移核的构造至关重要，不同的转移核构造方法，将产生不同的 MCMC 方法和目标状态转移的结果。目前常用的 MCMC 中抽样方法有三种，即MH算法(metropolis- hasting)、切片抽样(slice sampling)和吉布斯抽样(gibbs)，这三种方法各有优缺点[11]：MCMC最一般的抽样方法是MH方法。切片抽样是一种通过一个定义好的不变分布来构造可逆马尔科夫转移核的方法。Gibbs抽样是一种特殊的MH抽样，其随机数值总是被接收(即接收概率为1)，见图2。

MH方法是：取xi、xj两状态之间最小转移概率作为二者之间转入和转出的概率，那么，转出去概率大的状态增加了自我转移的概率。如图3所示，假设状态xi转出到状态xj的概率大。该算法能构造最快收敛，通过调整每个状态的自我转移概率，使它最接近稳态下的自我转移概率，多余的概率都转移出去，保证细致平稳条件。对于引航作业而言，使用MH算法可以快速收敛到目标状态，减少中间状态的过渡时间[14]。因此，使用该算法可以获得引航初始时和结束时的船舶状态。

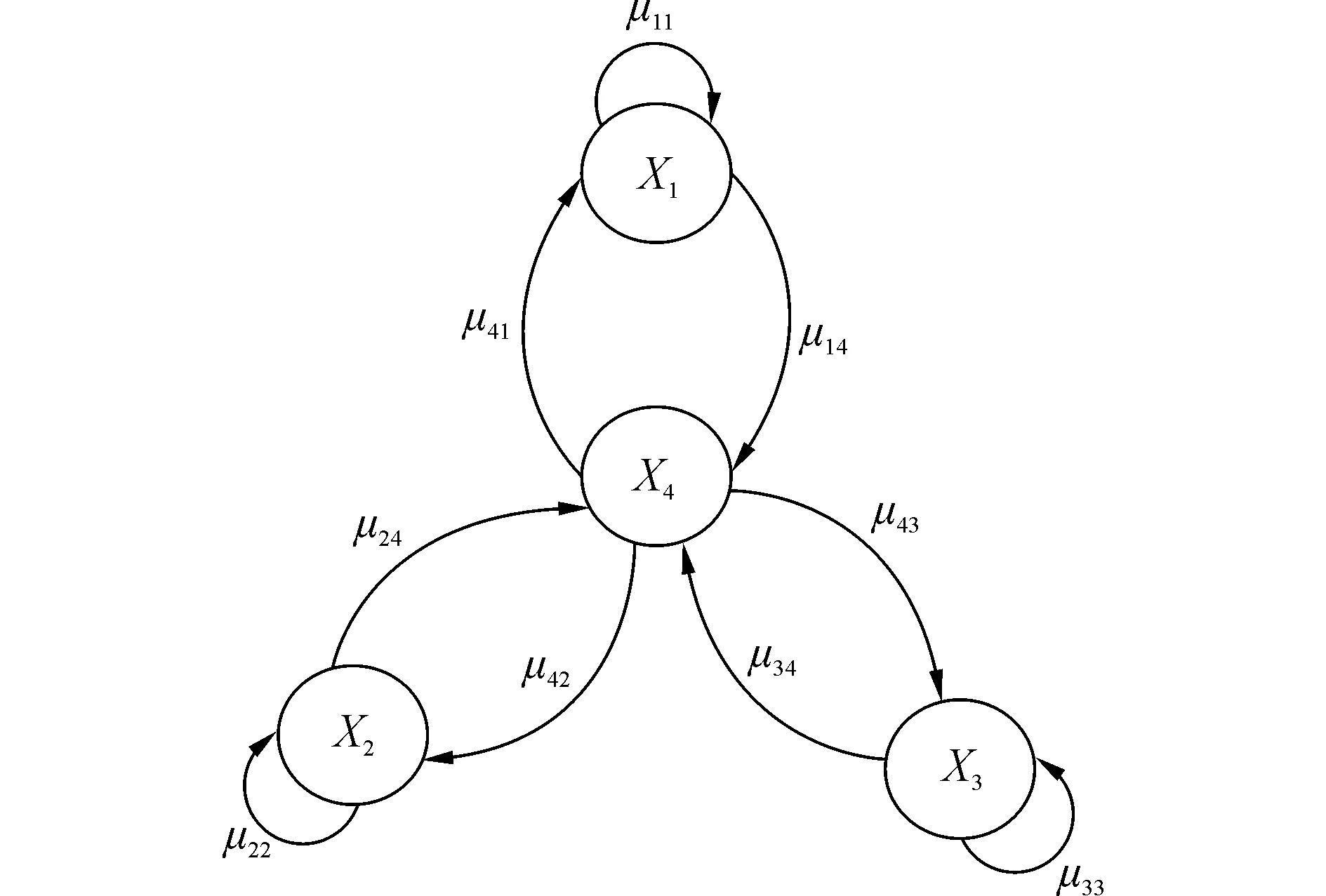
图2 船舶引航的状态转移变量Fig.2 Ship Pilotage state transition variable

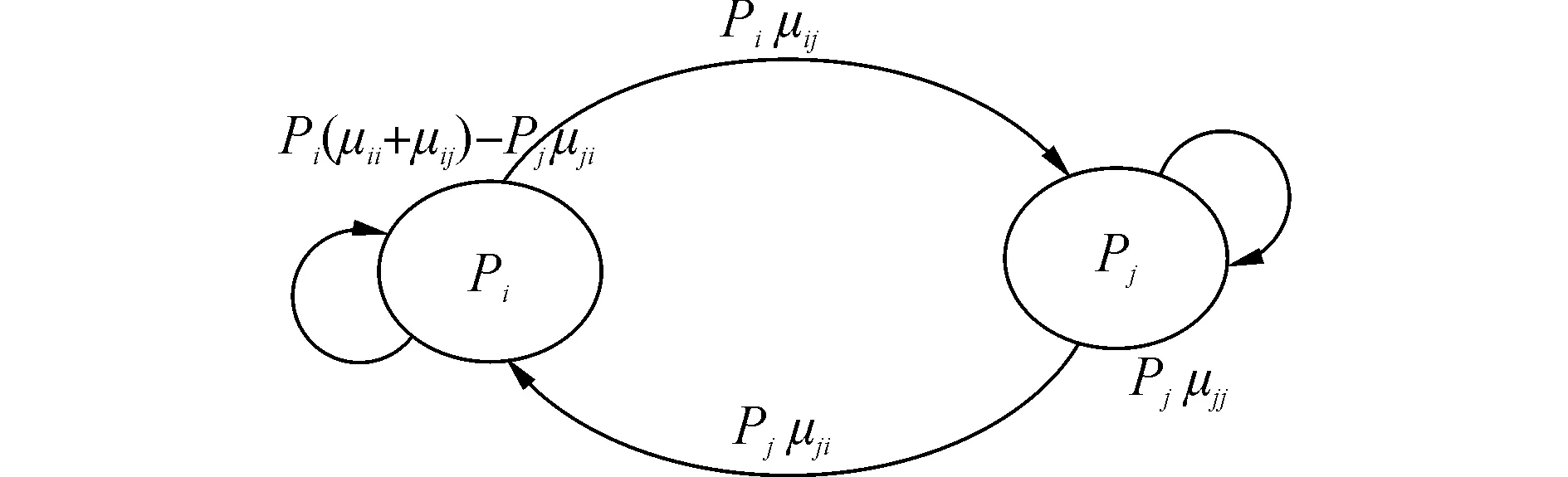
图3 MH算法的状态概率转移图Fig.3 State probability transition diagram on MH Algorithms

马尔科夫链的收敛性质主要由转移矩阵T决定，基于马尔科夫链做采样的关键问题是构造转移矩阵，使得平稳分布恰好是需要的分布S(x)。依照图3的算法，可以根据转移矩阵T⟹和 ⟸T来得到S(x)(t)和S(x)(t-1)的比率，进而按照一定的概率对两个样本进行选择。通过反复大量类似处理，最终得到样本符合原始的S(x)分布。

从一个高概率状态x(t)向一个低概率状态x(t-1)转移的概率与从这个低概率状态向高概率状态转移的概率相同。本文假设S(x)是一维标准高斯分布，xi是根据蒙特卡洛方法得到的一个样本，对此数据进行灰信息处理，使转移矩阵中行概率和为1。

本文选用 MH 算法对标准高斯分布进行采样，转移函数(非对称)是船舶进出港作业参数的高斯矩阵[16]。算法过程如下：

1)选取一个随机点S(0)，作为一个采样点。

2)选取随机点，确定转移函数为T，运用MH算法确定新的矩阵，进行灰性白化。

3)获取S(1)=S(0)T，然后对S(1)进行灰信息白化处理，进行S(1)中数据的归一化计算，获得新的S(1)。

4)求取R(1)=r·S(1)。

5)重复第1)～4)，获取S(n)=S(0)Tn，直至稳态R(n)=r·S(n)。

3 基于MCMC动态模型的船舶引航过程风险仿真

选用我国东部沿海某港区水域的船舶进出港数据来进行船舶引航风险仿真。选取的数据是2010-2015年间72个月的171 432艘船舶的引航作业。船舶种类包括集装箱船(60.07%)，化工品船舶(6.31%)，干散货船(30.55%)，其他(3.07%)。

3.1 样本的采集

表2为72个月中船舶引航任务按照进港、出港、移泊三种引航任务和外锚地、泊位、内锚地三个船舶初始状态统计基础数据。

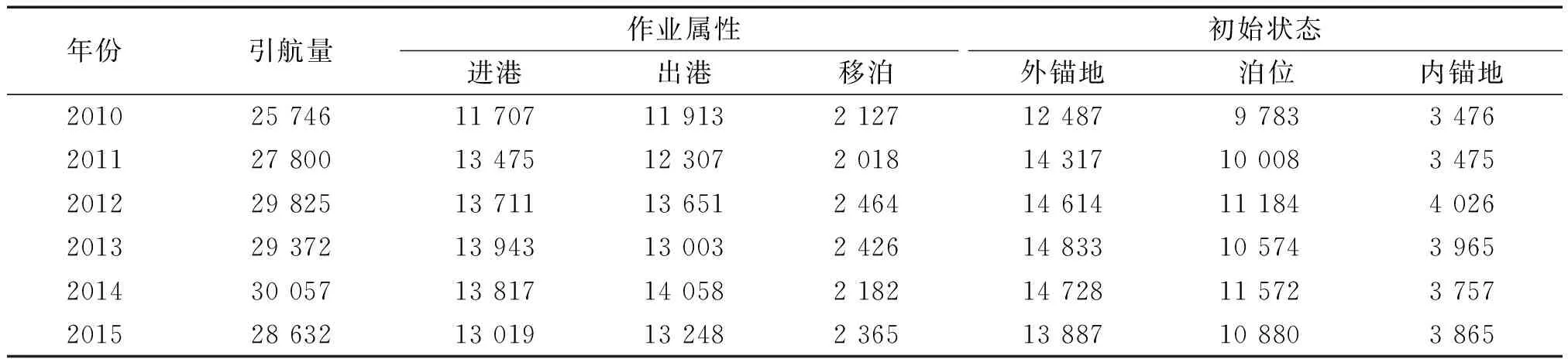
表2 港口船舶引航任务2010-2015年全年统计量

按每月的日均引航统计，得到31个不同日均引航进港、出港和移泊作业量分布。日均船舶量在44与117艘次之间，日均79.6艘次。然后，通过灰信息处理，获得归一化(一天的船舶量为100%)的不同日期的平均引航任务组成比率，如图4所示。

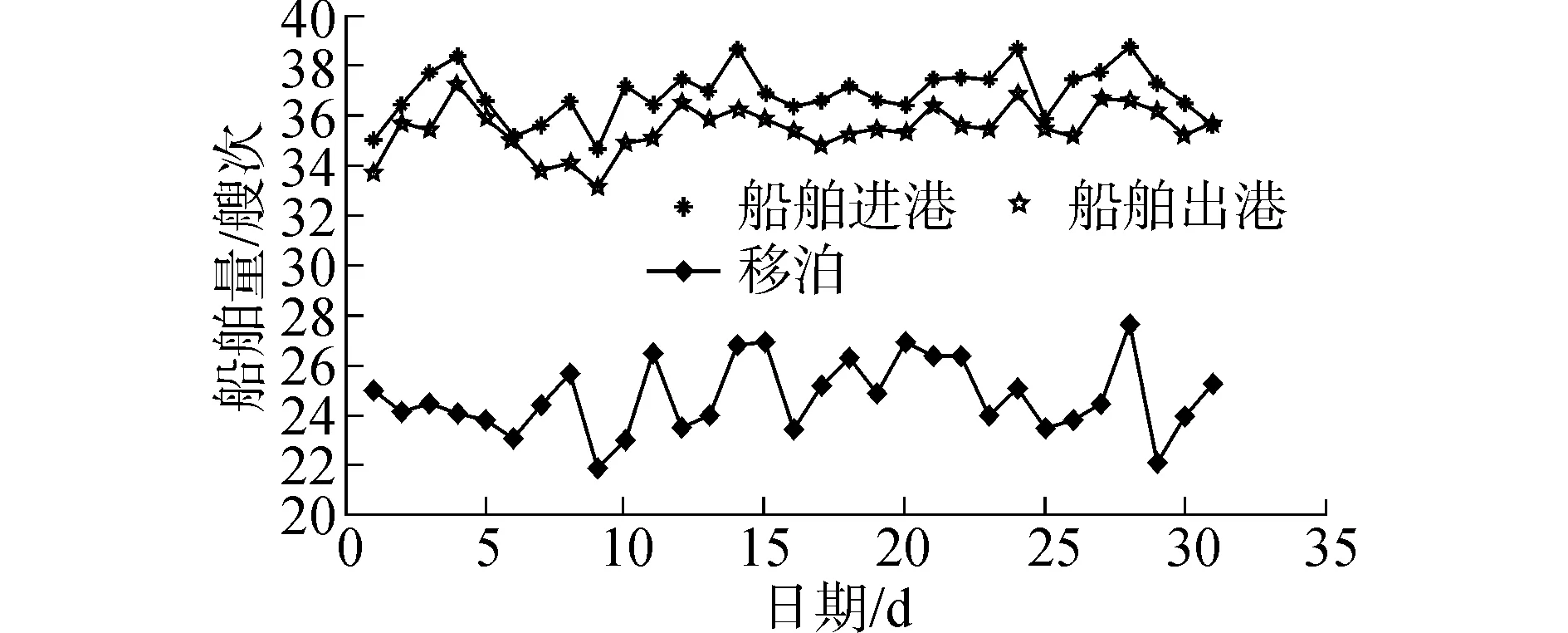
图4 某港区每日船舶引航不同作业属性的日均比例Fig.4 Ship daily activities at a certain harbour

3.2 动态仿真初始条件的设定

1)日均引航数据显示，进港、出港、移泊三种引航任务还是波动性强，具有随机性和不稳定性。假设不同任务下的比率符合高斯分布，那么确定t=0时船舶引航所处的初始状态为

(3)

2)确定船舶引航作业的风险值。依据文献[15]，对港口水域船舶航行、靠泊、离泊和移泊作业时发生的交通事故和作业量进行分别计算。经风险测量，再通过蒙特卡洛方法的仿真[15]，提出航行、靠泊、离泊和移泊的相对风险比值为6.9∶5.3∶5.1∶1.8。假设样本符合威布尔分布，可以计算出各种风险的分布参数。

按照表1的作业流程，可推理出内锚地、外锚地、泊位及前沿、港区航道四种状态下的风险值，然后通过归一化(相对风险量为100%)运算，得出风险状态矩阵r：

(4)

3)确定转移矩阵。在数据中统计同一水域的引航作业任务的比例，从而确定转移矩阵的相应变量值。这里先选定一个进出港平衡(对称)的转移矩阵T，数据已经完成了灰信息白化处理，获得下一个状态转移概率和为1。

在船舶进出港口中，状态转移是波动的，具有不稳定特性。若假定船舶在内外锚地、泊位及前沿、港区航道间的转移变量也符合高斯分布，那么对原始数据进行统计后，可确定随机转移矩阵变量值如表3所示，其他状态转移变量为0。考虑到转移矩阵中需要下一个状态转移概率和为1，因而对表3所确定的变量进行行归一化计算：

(5)

3.3 船舶引航过程马尔科夫链仿真

选用标准高斯分布进行采样，通过确定的船舶进出港作业参数的高斯矩阵(对称或者非对称)作为状态转移函数。因此，选定三个条件进行分析。

1)条件1：出多进少。进出港船舶数量不平衡，出港船舶多于进港船舶；

2)条件2：进出相当。进出港船舶数量平衡；

3)条件3：进多出少。进出港船舶数量不平衡，进港船舶多于出港船舶。

针对三种条件进行MC动态系统仿真，可以得到船舶港区水域流量分布和船舶引航动态风险数值。

表3 引航船舶状态转移变量

图5是在S(0)随机状态下进行不同状态转移条件下的船舶流量值，分别表示不同水域中在条件1、2、3下船舶流量分布。数据显示出：

1)在船舶引航状态的转移之初，船舶状态变化呈现很强的潮汐型波动，反映船舶引航作业的基本规律。船舶引航状态分布最终走向稳定，符合马氏稳态特性，同时港口船舶引航状态保持稳定。一般地，船舶状态在经历多次迁移，港区水域船舶的状态趋于稳定，航道流量占主体，约50%。即，对于港区运行而言，一般会保持在总流量的约50%数量的船舶在航道上航行。

2)船舶初始状态与稳定状态的关联不大，初始状态不影响最终的稳态。也就是，船舶引航任务的不确定不影响港口船舶流的分布。

3)船舶状态转移变量对港区水域总体船舶秩序影响明显。若船舶进港多于出港，那么最终锚地和泊位的船舶量趋于平衡，一般会均保持在总流量的约25%；若船舶出港多于进港，那么最终内锚地与泊位和港外锚地的船舶量趋于平衡，一般会均保持在总流量的约25%；若船舶进出港平衡，那么最终港区泊位与锚地和航道的船舶量趋于平衡，一般会均保持在总流量的约50%。

4)内锚地船舶流量不稳定，在10%以内波动。

图5 三个随机条件下不同状态转移后的船舶流量值Fig.5 Traffic flow under various ship activities with 3 random conditions

3.4 船舶引航过程风险的动态系统仿真

3.4.1 船舶引航过程风险蒙特卡罗仿真

若设定在不同水域船舶引航风险占总体风险值情况为r，如式(4)所示。设定航道水域有一定流量(中间态)，根据蒙特卡罗方法进行仿真，结果如图6所示。

1)由于在船舶引航状态的转移之初，船舶状态变化呈现很强的波动性，风险的波动性也很强，但趋势最终走向稳定。一般地，船舶状态在经历多次迁移，港区水域船舶的状态趋于稳定，航道引航风险(相对)数值约0.23。对于港区运行而言，不论进出港船舶比例如何，在航道上航行的船舶引航风险一般占主体。

2)船舶状态转移变量对港区水域船舶引航影响还是存在的。与进出港口船舶流量相当相比，若船舶出港多于进港，外锚地引航风险增加40%，泊位引航风险降低38%，内锚地引航风险降低50%；若船舶进港多于出港，外锚地引航风险降低40%，泊位引航风险增加25%，内锚地引航风险增加 1倍。

3)泊位水域引航作业的风险相对较高，尤其是进港船舶多于出港船舶时，风险(相对)数值达到0.091 3。

4)船舶引航作业受到船舶流结构影响。进港船舶比例较低时，内锚地和泊位前沿水域引航作业的风险相对低。随着结构比例增加，风险也上升；外锚地风险略有降低。

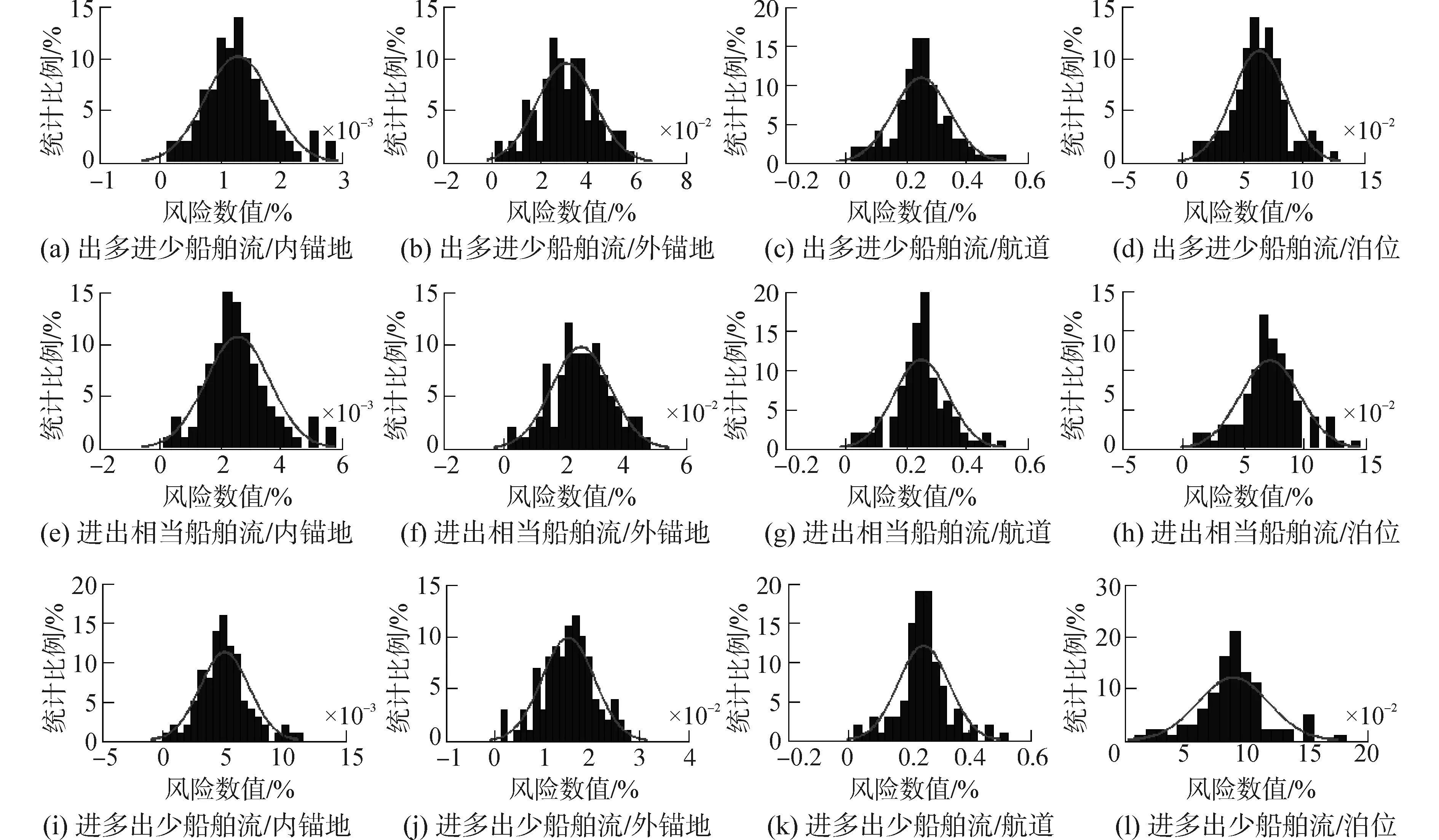
图6 不同状态转移条件下不同水域风险值Fig.6 Risk outcome under various ship activities and random condition

3.4.2 船舶引航过程风险MCMC仿真

引入MH算法，利用切片抽样快速收敛，对不同船舶进出港的流量引发船舶引航风险进行MCMC仿真，获得船舶引航作业初始状态和最终状态之间转移产生的风险，如图7所示。总体上，不同船舶进出港的流量引发船舶引航风险波动明显，但是趋势相同。作业量增加，风险趋于稳态。船舶进出港的流量不同，风险数值差异不大，船舶港区引航风险(相对)值接近0.32。

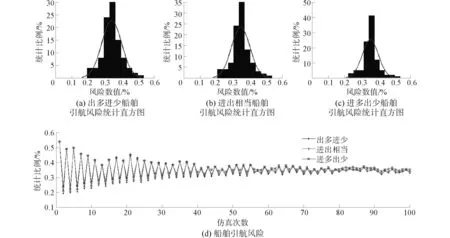
图7 不同船舶状态转移条件下风险值Fig.7 Risk outcome under random transition condition

3.5 风险动态系统仿真灵敏性分析

为测试MCMC的灵敏性，这里将初始状态S(0)，转移矩阵T和各状态下的风险值r都进行随机抽样，初始状态设定锚地和泊位前沿均有作业任务，转移矩阵按照表2来获取，运用MH算法进行快速收敛，可得到图8。

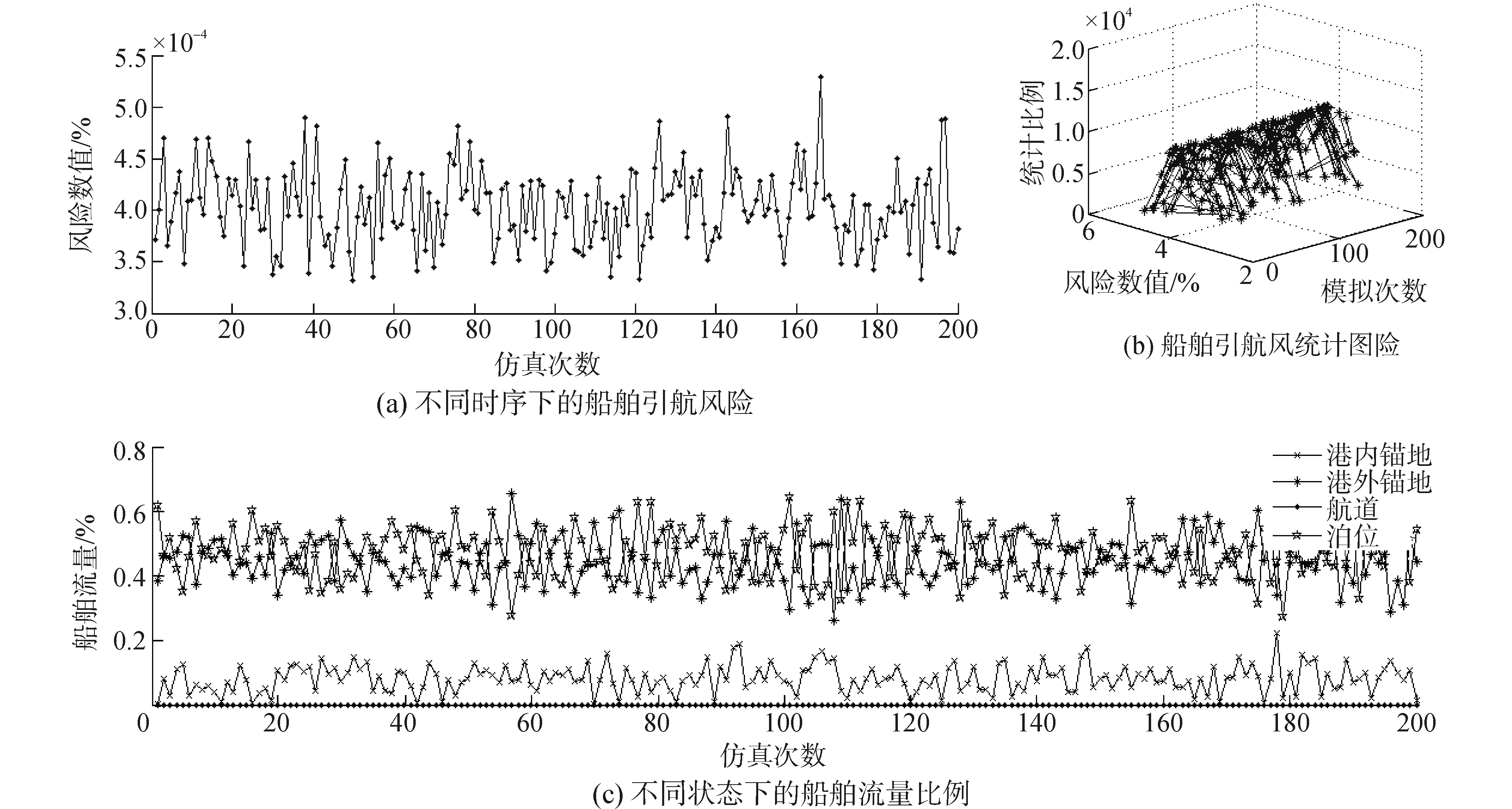
图8 船舶随机转移时船舶状态和风险值的灵敏性(引航任务分配时)Fig.8 Sensitivity on ship status and risk outcome under random transition condition

数据显示：总体上，船舶进港的流量稍大于出港流量，船舶流在50%左右波动。船舶进出港的日均流量变化引发船舶引航风险有波动，但波动幅度趋于收敛。

以上仿真情况表明，引入MCMC进行动态系统仿真，可以得到船舶动态风险趋于稳态的规律，港口水域船舶引航的风险(相对)大致在30%总体风险。鉴于目前港区船舶作业(含航行、靠离泊和移泊等作业)总体风险大致在2‰，那么单艘船引航风险维持在0.2‰～0.6‰的水平[13]。

引航实施过程中，将有部分船舶在航道水域，那么在四个水域均有一定比例的船舶流量，进行上述步骤的仿真，将得到港区水域整体的动态风险。经计算，得出以下结论：

1)尽管转移变量和作业次数变化，引航初始时，单艘次船舶引航风险值接近0.41‰的稳态；

2)引航实施过程中，单艘次船舶引航风险值接近0.67‰的稳态，结果如图9所示。图9(a)表示引航初始状态的风险(最终状态，收敛之后)，图9(b)表示引航实施中的风险(考虑中间状态，收敛之前)，横轴是风险值。

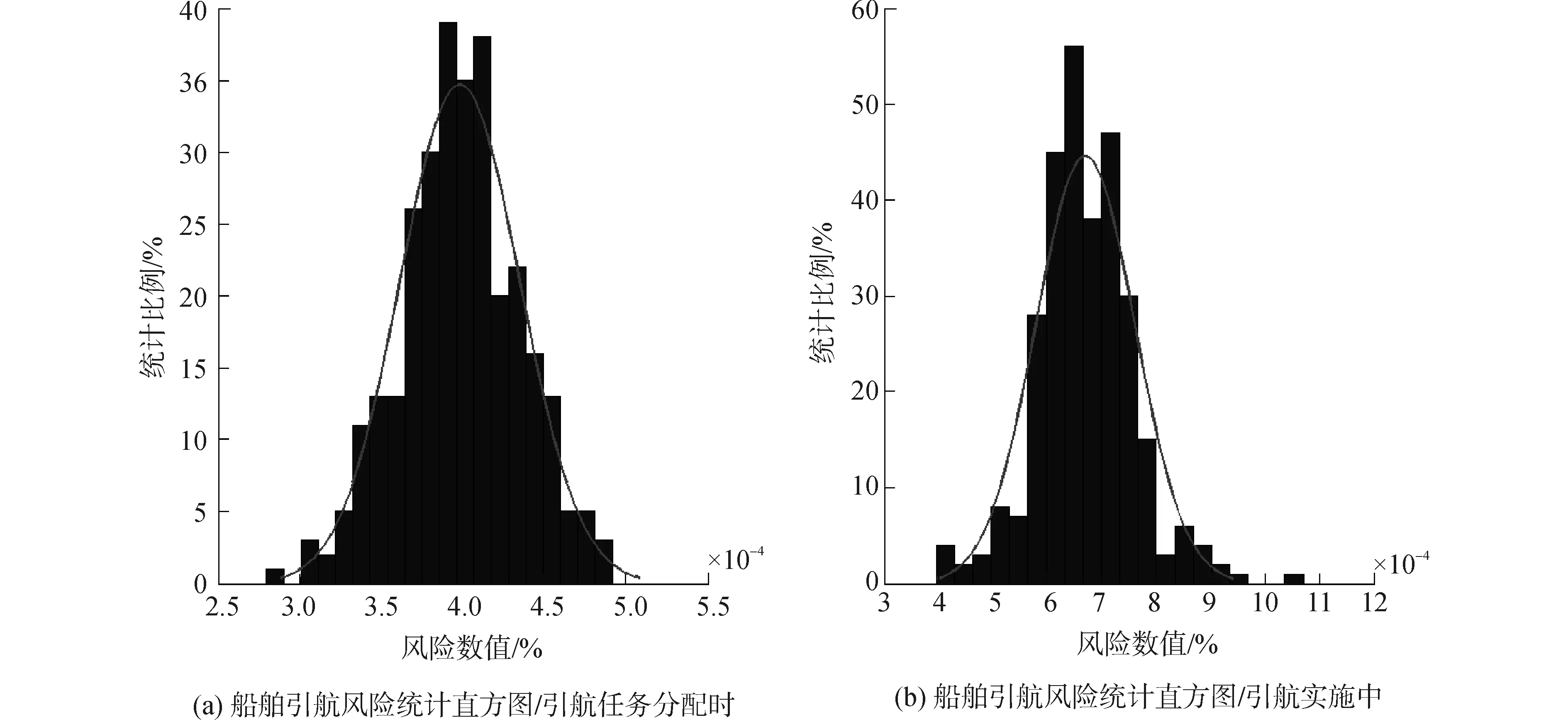
图9 不同时期风险值的灵敏性Fig.9 Sensitivity on risk outcome during initial and piloting

风险数值扩大是由于存在航道航行的风险和过程的实施风险。这一结论与船员及引航员的实践认识一致。

4 结论

1)提出了船舶引航过程的风险分析, 采用基于马尔科夫链蒙特卡洛方法进行动态系统仿真得到了港区水域船舶引航过程的动态风险宏观特征，特别是风险的稳定性表现形式。

2)相对于以往的风险评价，马尔科夫链蒙特卡洛模型适用于水上交通过程风险仿真与决策，克服事故特征和诱因获取的数据困难，在确定状态转移变量后，就能量化论证基于内部微观结构的水上交通宏观动态风险的变化趋势。

3)基于随机过程的分析方法可以研究港口船舶引航演化的基本规律，揭示港区水域船舶流量量化的分布状态，阐明港口船舶流量演化模式。

当然，下一步研究可以是具体船舶在状态转移条件下过程风险动态系统仿真，也可以是研究船舶连续时间和连续状态下马尔科夫过程的风险动态系统仿真，从而进行引航风险预警预控。

[1] COOK T, SHIPLEY P. Human factors studies of the working hours of UK ship′s pilots：A field study of fatigue[J]. Applied ergonomics, 1980, 11(2): 85-92.

[2] HU S, FANG Q, XIA H, et al. Formal safety assessment based on relative risks model in ship navigation[J]. Reliability engineering & system safety, 2007, 2(3): 369-377.

[3] FANG Q, HU S. Study on risk control of ship pilotage in Shanghai harbor[C]//Proceedings of the 4th IEEE International Conference on Management of Innovation and Technology, ICMIT., 2008, 1187-1192.

[4] 方泉根, 胡甚平. FSA在船舶引航风险评估中的应用[J].哈尔滨工程大学学报, 2006, 27(3): 229-334. FANG Quangen, HU Shenping. Application of formal satety assessment to the risk assessment of the ship- pilotage[J].Journal of Harbin Engineering University， 2006, 27(3): 329-334

[5] 方诚,胡甚平,方泉根. 港口船舶引航风险预测[J]. 中国航海, 2008, 31(4): 388-391. FANG Cheng, HU Shenping, FANG Quangen.Risk prediction of ship pilotage in harbor[J].Navigation of China, 2008, 31(4): 388-391.

[6] CAMERON J R. Improving the safety of marine pilotage[C]//2005 International Oil Spill Conference, IOSC， 2005： 3767-3771.

[7] 马飞,赵月林. 基于资产脆弱性风险评估模型的船舶引航安全评估[J]. 大连海事大学学报, 2008(S1): 17-19. MA Fei, ZHAO Yuelin. Ship pilotage safety assessment with the risk modal based on assets vulnerability[J]. Journal of Dalian Maritime University, 2008(S1): 17-19.

[8] WU Y, PENG G. Evaluation system of the portable pilot system based on fuzzy comprehensive evaluation[J]. Advanced materials research:manufacturing science and technology III., 2013, 622: 112-116.

[9] ÖMER F，SELMIN Z, BURAK. Formal safety assessment for ship traffic in the Istanbul Straits[J]. Procedia—social and behavioral sciences, 2015, 207: 252-261.

[10] PAK J, YEO G, OH S, et al. Port safety evaluation from a captain′s perspective: The Korean experience[J], Safety science, 2015, 72: 172-181.

[11] PRAETORIUS G, HOLLNAGEL E, DAHLMAN J. Modelling vessel traffic service to understand resilience in everyday operations[J]. Reliability engineering & system safety， 2015, 141: 10-21.

[12] 胡甚平, 黎法明, 席永涛,等. 海上交通系统风险成因耦合机理仿真[J]. 应用基础与工程科学学报, 2015(2): 409-419. HU Shenping, LI Faming, XI Yongtao,et al. Novel simulation on coupling mechanism of risk formation segments for marine traffic system [J]. Journal of basic and engineering, 2015(2): 409-419.

[13] FAGHIH R S, XIE M, NG K M. Accident risk assessment in marine transportation via markov modelling and markov Chain monte carlo simulation[J]. Ocean engineering, 2014, 91: 363-370.

[14] SCOLLNIK D P M. Actuarial modeling with MCMC and BUGS[J]. North American actuarial journal, 2001， (20)： 29-34.

[15] 胡甚平, 黄常海, 张浩. 基于云模型的海上交通系统风险蒙特卡洛仿真[J]. 中国安全科学学报, 2012, 22(4): 20-26. HU Shenping, HUANG Changhai, ZHANG Hao. Cloud model- based simulation of system risk of marine traffic by monte carlo algorithm[J]. China safety science journal, 2012, 22(4): 20-26.

[16] 王春峰, 万海辉, 李刚. 基于MCMC的金融市场风险VaR的估计[J]. 管理科学学报, 2000(2): 54-61. WANG Chunfeng, WAN Haihui, LI Gang. Estimation of value- at- risk using MCMC[J]. Journal of management sciences in China, 2000(2): 54-61.

Markovchainmodelforthedynamicsimulationofprocessriskinshippilotageatharbor

HU Shenping1, HUANG Changhai1, DENG Hua2, HUANG Daozheng3

(1.Merchant Marine College, Shanghai Maritime University, Shanghai 200135, China; 2.Marine Technology Department, Jiangsu Maritime Vocational Technology School, Nanjing 211170, China; 3.Transportation College, Shanghai Maritime University, Shanghai 200135, China)

10.11990/jheu.201605025

http://www.cnki.net/kcms/detail/23.1390.u.20170427.1510.082.html

X951

A

1006- 7043(2017)09- 1391- 08

2016-05-09. < class="emphasis_bold">网络出版日期

日期：2017-04-27.

中国博士后科学基金项目(2016M591651)；国家自然科学基金项目(51279099)；上海市自然科学基金项目(12ZR1412500).

胡甚平(1974-)，男，教授.

胡甚平，Email:Sphu@shmtu.edu.cn.

本文引用格式：胡甚平，黄常海，邓华，等. 船舶引航过程风险马尔科夫链模型动态仿真[J]. 哈尔滨工程大学学报， 2017， 38(9): 1391-1398.

HU Shenping, HUANG Changhai, DENG Hua, et al. Markov chain model for the dynamic simulation of process risk in ship pilotage at harbor[J]. Journal of Harbin Engineering University， 2017， 38(9): 1391-1398.