高空间分辨率遥感影像多尺度分割优化组合算法

许 飞，曹 鑫,2，陈学泓,2，崔喜红,2

(1. 北京师范大学 地表过程与资源生态国家重点实验室，北京 100875；2. 北京师范大学地理科学学部遥感科学与工程研究院，北京 100875)

0 引 言

高空间分辨率遥感影像提高了遥感技术监测地面信息的精细程度，被广泛应用于城市规划、土地资源调查等领域。然而，受光照条件、地形起伏等因素影响，高空间分辨率使遥感影像在监测同一地表覆盖类型时出现严重的光谱变异性，即“椒盐效应”（salt-andpepper effect）[1]。当使用基于像元的分类方法处理高空间分辨率遥感影像时，这种“椒盐效应”会使高分影像中同一种地表覆盖类型的分类结果出现误分，降低了分类方法提取地面目标的精度。影像分割算法是一种解决“椒盐效应”的图像处理算法，该方法对遥感影像的像元分割为若干个分割体，每个分割体内的像元均为同质性像元[2]。通过后续的分类、目标识别等影像处理过程，分割体可以被转换为具有特殊语义的对象[3]。在分割算法中，分割尺度决定了分割体容纳同质像元的能力，当分割尺度越大时，分割体内部像元的同质性越低，分割体的面积越大；当分割尺度越小时，分割体内部像元的同质性越高，分割体的面积越小。过小的分割尺度会使分割体无法容纳地面物体类内的光谱变异性，即无法克服“椒盐效应”的影响；过大的分割尺度会使分割体不但能容忍地面物体类内的光谱变异性，也能够容忍地物类间的变异性，导致分割体内部包含不同类别的像元，遗漏具有较小分割尺度的地面物体。因此，当影像分割算法被用于处理高空间分辨率遥感影像时，选择分割尺度是一个非常重要的问题。

目前，遥感影像的分割算法包括单一尺度的分割方法[4-6]和多尺度分割算法[1-2,7]。其中，单一尺度的分割方法不适用于地表覆盖条件复杂的遥感影像。在遥感影像中，不同类型的地面物体具有不同的物理空间尺度，因此，在遥感影像分割时，单一分割尺度无法同时刻画所有类型的地面物体。相反，多尺度分割允许同一幅遥感影像被不同大小的分割尺度分割，相比之下多尺度分割更具有实用性。此外，在处理高空间分辨率遥感影像的工作中，eCognition®[8]是一种被广泛使用的影像处理平台，该软件可以实现以多种尺度分割遥感影像的功能。

针对从多尺度影像分割中寻找影像中各种地物目标的最优尺度问题，本文提出了一种基于后验概率信息熵的多尺度分割组合算法MOCA（Multi-scalesegmentation Optimal Composition Algorithm）。该算法使用eCognition®对高空间分辨率遥感影像在多个尺度下进行分割，以分割体为单位计算不同分割尺度下高空间分辨率遥感影像内每个分割体的平均光谱。基于不同分割尺度下分割体的平均光谱，通过选取目标类型训练样本，使用分类器（本文中为支持向量机SVM[9]）生成不同分割尺度下的目标类型的后验概率，并计算不同分割尺度下的后验概率信息熵。最后，利用相邻分割尺度下信息熵指标的最大差分值寻找每个地面物体的最优分割尺度。本文使用F指标（Fmeasure）和BCI（Bidirectional Consistency Index）两种指标评估地面目标物提取精度，并将MOCA与同类多尺度分割方法进行比较。本文提出的MOCA算法试图实现多个分割尺度的最优组合，以期获得较高的地面目标物提取精度。

1 实验算法

本文提出了一种多尺度分割优化组合方法MOCA，其基本过程包括计算像元级后验概率矢量、遥感影像的多尺度分割、计算不同分割尺度分割体的后验概率信息熵、建立后验概率信息熵最大差分指标、逐对象选择最优分割尺度。

1）计算像元级后验概率矢量以及对高分影像进行多尺度分割

本文提出的方法需要计算多尺度分割结果中每个分割体的后验概率矢量。首先，本文使用支持向量机（SVM）计算单个像元的后验概率矢量。计算时，本文分别对树木、草地、屋顶、道路和水体每种地表覆盖类型选择3000～5000个像元作为训练样本，将训练样本输入至SVM分类器中得到像元级后验概率矢量。与此同时，本文使用eCognition 8.9软件对遥感影像进行多级尺度分割。分割时，形状因子设置为0.2，紧致度因子设置为0.5。此外，影像的DN值的数量级决定了eCognition分割尺度的范围。以HYDICE数据为例，本文以10为步长，从50递增至1000，最终被选择的多级分割尺度为50，60，70，80，…，970，980，990，1000。基于以上参数，本文在eCognition 8.9软件中利用MRS (multiresolution segmentation)算法创建规则集，生成高空间分辨率遥感影像在不同分割尺度下的分割结果。

然后，将eCognition生成的多尺度分割结果生成编号文件，以分割尺度为顺序依次导出为栅格数据，其中栅格数据中每个像素对应的值就是该像元所在分割体的编号。基于上述步骤获得的eCognition多尺度分割结果，以及像元级后验概率矢量，可计算每一个分割尺度下各分割体的平均后验概率矢量，最终得到每个地面物体在所有分割尺度的平均后验概率。其中，对于某一分割尺度上的一个分割体而言，其后验概率矢量可以表示如下：

2）建立后验概率信息熵最大差分值指标

在不同分割尺度的分割结果中，总有一个面积最大的分割体Simax覆盖地面物体i。随着分割尺度的增加，不同类别的像元融入Simax，导致Simax的平均后验概率矢量随着分割尺度的增加发生变化。后验概率信息熵[10]能够将分割体的后验概率矢量转换为分割体的类别纯净度指标；Simax的后验概率信息熵随着分割尺度的变化信息也能够代表Simax内部像元纯净度的变化。

本文对所有地面物体的Smax按照分割尺度的递增顺序分别计算其后验概率信息熵。后验概率信息熵的计算方法如下：

式中，Pi表示分割体属于第i类的后验概率，n代表总类别个数。当分割体处于过分割时（即分割尺度较小时），分割体内所包含的类别单一，后验概率信息熵值较小；当分割体处于低分割（即分割尺度较大时），分割体内包含的类别丰富，后验概率信息熵值较大。随着分割体在不同尺度下形状大小的变化，分割体的后验概率信息熵也发生变化。分割尺度的增减直接影响分割体内部像元类别多样性的变化，因此，地面物体分割尺度的变化等价于地面物体所在分割体的后验概率的变化。为了进一步探究后验概率对信息熵指标的影响，本文假设两种地表覆盖类别的情况（两种地表覆盖的后验概率分别为P1和P2），其中P1为目标地物真实类别的后验概率，P0为目标地物周围其他类别的后验概率，信息熵的变化可以表达如下：

式中，Ei代表在第i分割尺度下分割体的后验概率信息熵，1代表第i分割尺度和第i+1分割尺度的分割体的后验概率差分值。

本文通过eCognition生成高空间分辨率遥感影像在50，60，70，…，980，990，1000分割尺度下的分割结果，通过前文所述的计算过程得到这些分割尺度下的后验概率信息熵序列 。本文基于公式（4）计算出每一个地面物体在不同的相邻分割尺度下的后验概率信息熵序列，并找到|△E|i,i+1最大的分割尺度作为当前地面物体的最佳分割尺度，保存该物体在最佳分割尺度的分割体，最后合并遥感影像中所有地面物体的最佳分割体，形成多尺度分割结果。MOCA算法流程如图1所示。

图1 MOCA算法流程Fig.1 Flow chart of MOCA method

2 精度评价指标

遥感影像分割结果的评判方法包括目视解译法和定量判别法。在使用定量判别方法时，本文首先对研究区域的遥感影像进行手工数字化，生成地面物体的理想分割体，用于评价多尺度分割算法生成分割体的准确性。本文使用 BCI（Bidirectional Consistency Index）指标[11]和F指标（Fmeasure）[12]评价多尺度分割结果。F指标和BCI的计算公式如下：

式中，Si表示高空间分辨率遥感影像分割结果的第i个分割体，Simax表示Ri覆盖区域的面积最大的分割体；Ri表示对应于Si的参考分割体，Rimax表示Si覆盖区域的面积最大的参考分割体。F指标和BCI的值越高，代表实验生成的分割结果越符合地面物体的最优分割结果。

3 实验结果与分析

3.1 实验数据

本文使用了两幅高空间分辨率遥感影像，其中一幅高分影像为华盛顿特区的HYDICE高空间分辨率高光谱影像，另一幅为北京地区的Quickbird高空间分辨率影像。如图2所示，HYDICE和Quickbird高分影像中包括水体、道路、草坪、屋顶等地面物体。此外，HYDICE和Quickbird高空间分辨率遥感影像的过分割结果与低分割结果都无法恰当地刻画研究区域的地面物体。度分割算法[13]以及MOCA算法对HYDICE影像和Quickbird影像进行分割，并使用F指标和BCI对每种方法生成的分割结果进行评估和对比。MOCA算法得到的分割尺度最优组合结果如图3所示，图3中HYDICE数据与Quickbird数据的“参考分割结果”是手工数字化参考分割体；图3的“MOCA分割结果”为本文算法得到的多尺度分割结果。为了体现MOCA能够得到对象级的最优分割尺度，图3给出了HYDICE和Quickbird的分割尺度分布图，其中每个分割体都具有不同的分割尺度。需要补充说明的是，由于道路和一些线状分布的行道树实际的物理尺度可能远远大于本文设定的分割尺度，为了更准确地对比不同方法的分割精度，本文在手工数字化参考分割体中剔除了道路和线状分布的行道树，只保留了雕像、屋顶、停车场、草坪、湖泊等地面物体。

图2 HYDICE高光谱高空间分辨率遥感影像与Quickbird多光谱高空间分辨率遥感影像及其过分割与低分割结果Fig.2 High spatial resolution images of HYDICE and Quickbird, and the over-segmented and under-segmented results of HYDICE and Quickbird

图3 MOCA算法最优分割尺度组合结果Fig.3 Optimal multi-scale-segmentation composition results by MOCA

3.2 实验结果及分析

本文首先利用MOCA算法对HYDICE影像和Quickbird影像分别进行多尺度分割优化组合，得到影像中每一个地面对象的分割体，利用F指标和BCI对算法生成分割体的准确性进行定量评价，并对比了单一尺度分割算法和稳定区间多尺度分割算法[13]。然后，本文讨论了eCognition多级分割尺度的步长与SVM分类器的训练样本量对MOCA算法分割精度的影响。

3.2.1 分割结果及精度评价

本文分别使用单一尺度分割方法、稳定区间多尺

根据图3显示的多尺度分割结果，可认为MOCA算法得到的分割结果与地面物体的理想分割体具有较高的吻合度。此外，本文使用F指标和BCI两种指标定量评价了三种方法在同一区域的分割结果，定量评估结果见表1。通过定量对比实验，本文得出MOCA算法比单一分割尺度、基于稳定区间的多尺度分割算法具有更高的分割精度。

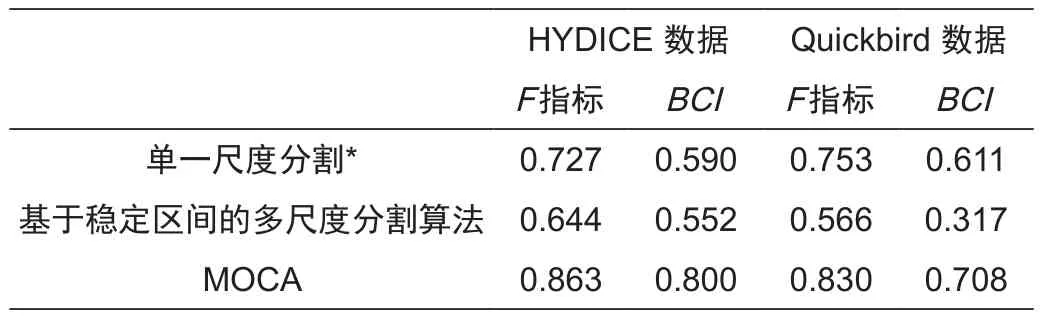
表1 定量评定结果Tab.1 Assessment of segmentation accuracy

3.2.2 参数敏感性分析

MOCA算法涉及两个关键参数，eCognition生成多级分割尺度分割结果的尺度步长、SVM分类器的训练样本量。这两种参数可能会对多尺度分割算法最终的分割精度产生影响，因此本文使用控制变量法，分别使用不同梯度的分割尺度步长和不同梯度的SVM分类器的训练样本量对HYDICE数据进行分割，并统计不同输入参数下的分割精度。参数变化对分割结果的影响见表2。

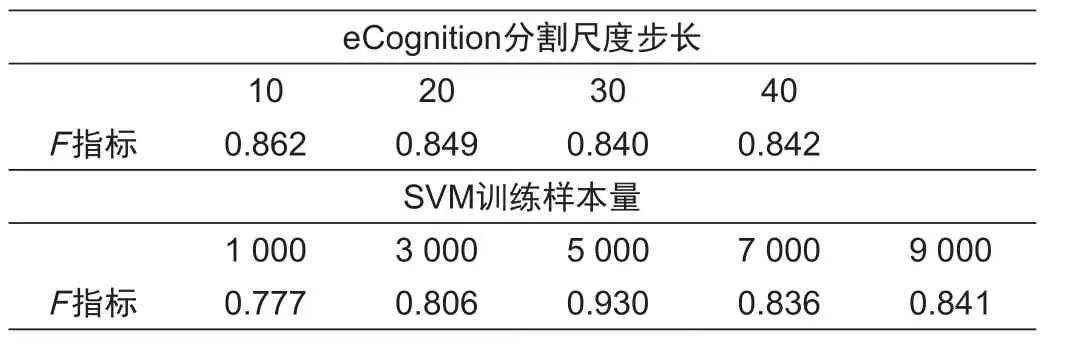
表2 参数变化对分割精度的影响Tab.2 The impact of parameters on accuracy of segmentation

本文根据表2得出以下结论：MOCA算法对eCognition分割尺度步长的变化敏感性较低，eCognition分割尺度步长越小，该算法得出的分割精度越高；SVM分类器的训练样本量对本文算法分割精度具有较强的敏感性，当每种地表覆盖类型的训练样本量为5 000个像元时，本文算法的分割精度最高。

4 结束语

本文针对高空间分辨率遥感影像设计了一种基于后验概率信息熵的多尺度分割优化组合算法MOCA。通过华盛顿地区的HYDICE高光谱高空间分辨率遥感影像和北京地区QuickBird多光谱影像进行实验，对分割结果的目视判别和定量评估，表明MOCA能够同时适用于高光谱和多光谱高空间分辨率遥感影像的分割工作，并且能得到相对较好的分割精度。此外，本文对该算法涉及到的两种参数进行了精度敏感性实验，证明了该算法对eCognition多尺度分割步长不敏感，当SVM分类器训练样本量为5000时该算法能得到最高的分类精度。