基于球面退化四叉树格网的GlobeLand30数据表达及精度分析

朱思坤，赵学胜

(中国矿业大学（北京）地球科学与测绘工程学院，北京 100083)

0 引 言

全球地表覆盖分布及变化是气候变化研究、生态环境评估、地理国情监测、宏观调控分析等不可或缺的一项重要基础信息[1]。我国自主研制了世界上首套30 m空间分辨率的全球地表覆盖数据集GlobeLand30，用于支持全球可持续发展和应对气候变化。GlobeLand30采用通用横轴墨卡托投影（UTM）分幅组织数据，按6°经差分带投影，全球分为60个投影带，共853幅数据[2-3]。UTM投影为等角投影，为了保持较小的长度和面积变形而采用分带投影的方法，分别将每一投影带按照中央子午线两侧一定经差范围内的椭球面正形投影于椭圆柱面[4-5]。这样做可以保证投影之后的每一个投影带内的几何变形较小，但是实际上也造成了空间数据的断裂和重叠，导致全球空间数据实体的不连续[6-9]。如在研究一些具有明确边界划分的大尺度范围问题时，往往采用矢量多边形表示研究区域，而这些矢量数据为了保证数据的连续性无法采用UTM投影、高斯投影这样的分带投影，因这些投影方法每个投影带都有各自坐标系，投影空间上并不连续[10]。实际利用矢量提取研究区域数据时只能选择根据投影分带图幅范围裁切矢量数据，并将裁切后的矢量数据投影至与之匹配的投影带，如文献[11-12]中采用了先将待统计区域的矢量数据的弧段进行线性内插的方法，这样就需要对每一幅数据分别处理，当研究大尺度范围时数据量很大，过程往往比较繁琐，处理效率低下。

为了解决上述问题，本文拟采用全球退化四叉树格网（Degenerate Quadtree Grid, DQG）代替原始地图投影重新组织GlobeLand30，利用全球离散格网模型统一、连续、无缝、高效地表达地表覆盖信息[13-17]。特别是DQG格网与其他球面离散格网相比，具有结构简单、几何变形稳定、广泛的数据兼容性、层次性、径向对称性、方向一致性等优点，便于聚类、统计分析、层次索引以及多分辨率的数据组织等操作[18-22]。最后选取典型区域及相应的数据质量评价指标，对比分析了GlobeLand30数据在UTM投影模式及DQG格网模式的定量化统计表达精度。

1 数据表达与组织模型

1.1 DQG剖分模型

首先选取球内接正八面体作为球面格网划分的基础，首次剖分将球面划分成八个完全相等的球面三角形，称为八分体。以一个八分体为例，应用退化四叉树剖分方法，将八分体的三条边按经纬度平分，连接两腰上的中点之间的纬线，再将该纬线中点与底边中点以经线连接，形成一个新的子球面三角形和两个球面四边形，为第一层剖分结果；第二层剖分时，球面三角形仍然按第一层剖分方法，子四边形按照常规四叉树剖分方法进行剖分；第三层重复第二层剖分方法……依次进行递归剖分，直到满足一定分辨率要求为止，一个八分体的前三层剖分规则如图1所示，第三、四、五层全球剖分格网示意图如图2所示。详细剖分方法以及编码规则参考文献[23]中有具体论述。

图1 DQG剖分原理Fig.1 Subdivision schemes of DQG

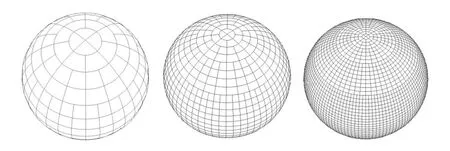
图2 第三、四、五层全球DQG剖分结果Fig.2 DQG subdivision in diあerent levels(the 3rd,4th,5th level)

1.2 剖分层次的确定

以球面离散格网模型代替地图投影表达GlobeLand30，首先需要确定平面投影数据分辨率与DQG剖分层次的对应关系。格网模型按照其固定剖分方法可以无限细分，直到达到模拟地表信息的目的，即达到分辨率要求。本文在按照退化四叉树的方式剖分球面时，按照“转换后的DQG格网单元小于原始数据栅格单元”的原则，剖分格网可达到更高分辨率，充分保留了原始数据的空间信息。原始数据的空间分辨率为30 m，按照公式(1)计算确定其所对应的格网层次：

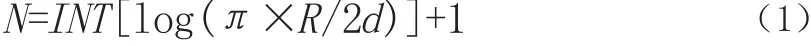
式中，INT为取整运算，R为地球半径，d为原始数据分辨率，N为对应的DQG剖分层次。根据公式确定选取第19层DQG表达原始数据，实现数据从地图投影到DQG模型的转换。

1.3 格网数据表达规则

由于GlobeLand30为分类后结果，属于离散的定性地理空间数据，利用球面格网重新表达时，格网赋值地类必须唯一确定且与原始数据分类结果相吻合，不能出现地表覆盖结果的疏漏或增加。因此，本文选取最近邻重采样方法，以格网中心点为采样点确定格网所对应的地表覆盖类型，生成格网模型数据结果。具体方法为：

1）首先根据DQG地址码确定格网中心点坐标，详细DQG地址码与经纬度坐标的转换方法见参考文献[24]文中所述。

2）将第19层DQG的格网中心点投影到原始数据投影空间中，确定格网中心点地表覆盖类型。

3）将格网所属地表覆盖类型赋值为格网中心点在原始数据中的地表覆盖类型，得到格网模型数据结果。

1.4 格网数据的分块组织

由于计算机处理能力的限制，不可能将海量的大范围空间数据一次性装入内存处理，必须对数据进行分块处理。为了同时兼顾高效的数据存取与数据查询操作，以第6层DQG格网范围分块组织转换后的数据。即以第6层格网范围无缝组织成数据瓦片，对于每一块格网瓦片，以转换后的第19层格网单元作为基本像元，每一块瓦片数据包含8 192×8 192个格网像元。以该格网瓦片对应的唯一编码命名数据，并以文件夹的方式保存数据结果。

2 实验与分析

DQG本质上属于变经纬度格网，为了保证格网单元面积的近似相等而采取了随纬度由低到高逐区退化的操作。对基于DQG重新表达后的GlobeLand30进行地学统计时，应考虑到DQG格网单元的非均匀性、变形分布的不规则性对空间采样合理性和统计精度的影响。以往DQG格网研究主要探讨了格网模型几何属性的总体变化特性，对格网几何变形的空间位置分布的定量化研究较少，同时也缺乏相应精度评定标准。为此，本文选取球面上不同区域地理实体作为研究样本，以采样点变化率为指标分析DQG模型的空间采样合理性以及其对数据转换精度的影响；并以区域总面积变化、各地类构成占比等指标分析统计精度变化。

2.1 空间采样合理性分析

为了在实际应用时控制误差，需分析数据转换精度随DQG格网空间位置分布的变化规律。由于DQG格网单元大小主要随瓦片数据的纬度范围变化，所以，选取N45带原始数据（如图3所示）进行实验，转换生成DQG瓦片数据结果（如图4所示）。分别对每块原始数据按均匀分布随机生成三组不同数量级的变化检验点，进行抽样调查，比较采样点在原始数据中的地表覆盖类型与其在DQG模型数据中的地表覆盖类型变化。以采样点平均变化率（地表覆盖类型变化点数/总抽样点数）为指标，分析DQG表达原始数据的精度变化，结果见表1。

图3 GlobeLand30平面投影模型Fig.3 Projection model of GlobeLand30

图4 DQG球面数据模型Fig.4 Sphere model of DQG

表1 数据转换精度随空间位置分布Tab.1 Spatial distribution of data conversion accuracy

从实验结果可以看出：三组对照实验结果都相差不大，结果一致，说明随机采样实验结果可信。在球面不同纬度区域内，采样点变化率与格网单元大小关系密切，格网单元越小，采样点变化率越小。整体上看，虽然数据转换精度由于DQG格网单元的面积不均匀分布而随之变化，但由于剖分层次较高，如前所述，所有格网单元均小于原始数据像元，总体数据变化率较小，最小低于1%，最高也只有5%左右。

2.2 地表覆盖统计精度分析

选取0～45°区、跨退化区内代表性地理实体分别为：西藏(0～45°)、新疆（跨退化区）作为研究区域。由UTM投影数据转换生成DQG瓦片数据，以格网单元球面面积代替投影面积计算统计，并以原始数据在等积圆柱投影下统计结果作为理论参考值，检验DQG数据的精度和度量准确性，区域总面积统计结果见表2、表3，各类地表覆盖面积占比统计结果见表4。

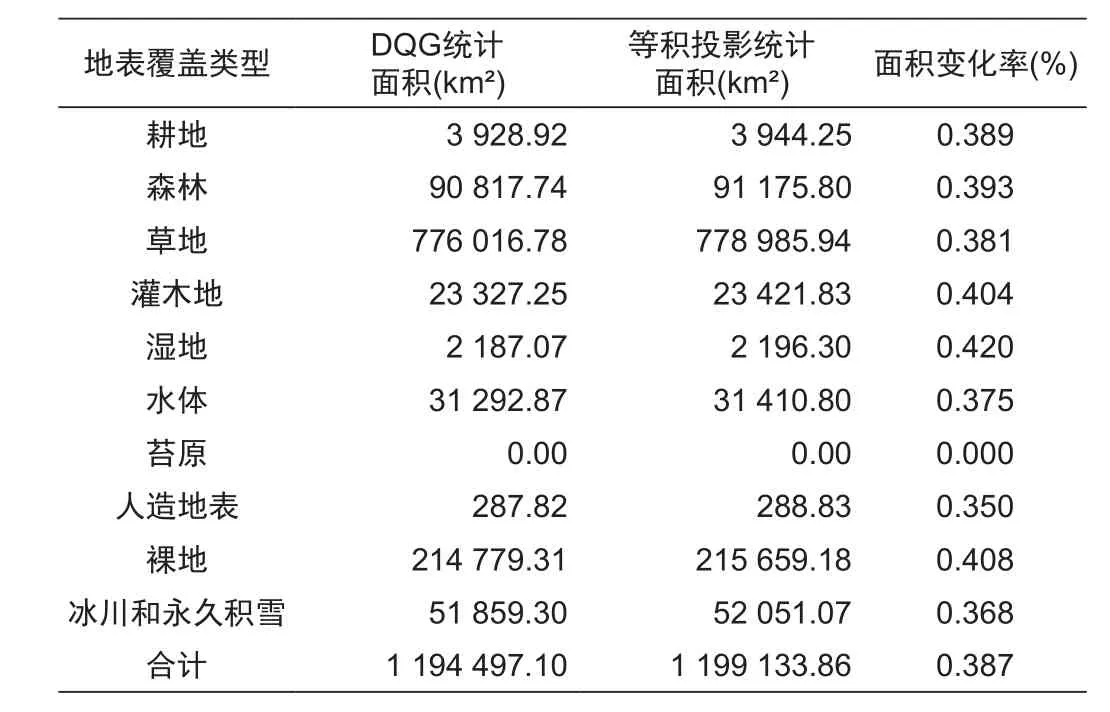
表2 西藏地表覆盖面积统计Tab.2 Land cover area statistics in Tibet

表3 新疆地表覆盖面积统计Tab.3 Land cover area statistics in Xinjiang

表4 西藏和新疆地表覆盖构成占比统计Tab.4 Land cover proportion statistics in Tibet and Xinjiang

从表中可以看出：①无论处于球面哪一个区域，格网模型总面积统计结果与等积投影统计结果（理论参考值）相差都很小，面积变形率小于1%，保证了DQG面积度量的准确性；②每一个研究区域内，每一类地表覆盖数据的格网模型统计结果也都与理论值相差很小，而且其面积变化率都与总面积变化率一致，说明总体上各类地表覆盖面积变形趋势一致；③除了DQG模型面积统计结果变化很小之外，每一类地表覆盖面积占比几乎不变化。

3 结束语

本文以全球离散格网为基础重新组织表达GlobeLand30数据，研究了基于DQG格网框架的数据应用与分析模式。在无缝高效地表达地表覆盖信息的基础上，分析了基于DQG应用GlobeLand30的数据转换精度以及可靠性，得到以下结论：

1）基于DQG代替地图投影表达GlobeLand30数据，有效解决了投影过程带来的数据断裂、两极数据变形较大等一系列问题；特别是DQG本质上是一种变间隔的经纬度格网，与GlobeLand30数据的原有经纬度存储格式基本一致，数据转换简单直接，可以作为一种GlobeLand30数据的有效组织和表达模式。

2）通过确定格网模型质量评价指标与误差控制方法，基于DQG统计分析地表覆盖信息的结果能够保持原始数据的精度，满足大多数实际应用需要。

实验分析发现格网模型的单元面积直接影响数据表达精度，虽然可以通过整体系统控制手段减小误差，但是对变形及误差的具体分布规律以及定量化表达还只是初步探索性的，并且精度评价标准的选择也是根据特定的应用需求，仍需进一步研究构建一整套球面格网系统的可靠性评估模型与质量控制方法。