四层结构的模糊神经网络电梯群控算法研究及程序实现

许英杰 潘廷哲 胡志男 黄景山

四层结构的模糊神经网络电梯群控算法研究及程序实现

许英杰1潘廷哲1胡志男2黄景山1

（1.厦门大学航空航天学院 厦门 361005）（2.厦门大学物理科学与技术学院 厦门 361005）

为提高电梯群控系统的载客效率，减少系统运行能耗，提高运行稳定性，在传统模糊神经网络算法的原理上，设计了基于电梯群控模糊规则的四层模糊神经网络算法，确定四层模糊神经网络结构，定义模糊规则，测算隶属数值，推导隶属度函数，并且基于Matlab提出算法检验方案，给出验证结果。最后采用结构化编程思路在PLC中实现控制程序，并提出可变响应闭环的程序实现方式。

电梯群控；模糊控制；四层神经网络；Matlab建模仿真检验

AbstractIn order to improve passenger carrying efficiency of the elevator group control system，reduce system energy con⁃sumption and improve the stability of the operation，a four-layer neural network algorithm based on the algorithm principle of tradi⁃tional fuzzy neural network is designed.The implementation includes determining four fuzzy neural network structure，defining the fuzzy rules，calculating the membership value，deriving the membership function and presenting the results through Matlab pro⁃gram.Finally，elevator control program is designed through the structured programming method in PLC and a variable response of the closed-loop programming method is proposed.

Key Wordselevator group control，fuzzy control，four-layer neural network，Matlab modeling and simulation

Class NumberTP301.6

1 引言

城市现代化建设离不开电梯。随着近年来建筑楼层逐步提高，电梯层数、梯数不断增加，电梯使用频率也不断提高。确保电梯稳定、高效、节能运行成为电梯研究的重点。电梯群控系统（EGCS）具有随机性、非线性，难以通过建立精确模型完成推导控制，需要通过研究电梯的调度特性，择取一种最优控制算法，并实现理论仿真及实践验证。

2 算法选择

电梯的算法有多种，其中研究较为完善地包括基于神经网络的控制算法、基于模糊逻辑的控制算法、基于遗传算法的控制算法［1］、多目标优化控制算法、基于排队论的控制算法［2］、基于模糊神经网络的控制算法［3］。综合比较，神经网络算法结构庞大，网络训练样本较多［4］，因此结果的合理性难以验证；基于模糊逻辑的控制算法性能主要取决于专家系统，专家认定的模糊规则不完全适用于各类型电梯，缺乏对问题及环境的适应性；基于遗传算法的控制算法本身所具有的随机性使其搜索进程效率不高，其优良的搜索结果是以尽可能长的搜索时间为代价的，对于电梯响应度高、随机性大、控制器性能有限的情况，并不能发挥最优效果；多目标优化控制算法，优化目标和权重需要自行设定，稳定性不高；排队论适合于高峰期情况，对于平均候梯时间有明显的改善，但是对于平均乘梯时间和整体能耗两个指标考虑略少［5］。

模糊神经网络控制算法［6］较之其他算法更为完善，可在不清楚函数自变量之间的内部关系的条件下，根据电梯特性制定出符合当前情况的最优解。

3 模糊神经网络算法研究

模糊神经网络由三部分构成：输入层、隐层（包含两层结构）和输出层［7］。基于神经网络结构，通过灰色系统预测出电梯的平均乘梯时间、平均候梯时间、电梯运行能耗各参数关系，通过模糊规则求解电梯的隶属函数值，最终进行反向求解，求出电梯的平均乘梯时间、平均候梯时间、电梯能耗的权重值w1，w2，w3，确定目标隶属函数，实现电梯的最优调度。

3.1 四层神经网络架构确定

神经网络用以调度电梯状态之间以及目标结果之间的联系，由于网络内部具体联系的法则不可准确预知，需采用模糊规则调度原则，以达到对当前情况的最优选择和对未来情况的准确预测。如图1所示，神经网络采用一个输入层，用于将每部电梯的状态总量 (X1，X2，…，Xn)，即电梯最长乘梯时间、最长候梯时间和启停次数传送到模糊神经网络的第二层；第二层为隶属函数层，包含每部电梯的平均乘梯时间ART、平均候梯时间AWT、整体能耗EC；第三层是用于计算每条规则适用度的规则层，每个节点表示一条模糊规则，其模糊规则由电梯的运行机制与逻辑运行的合理性确定；第四层为输出层，用于归一化计算每部电梯通过模糊规则确定的神经网络联系，最终得出的隶属度函数值。

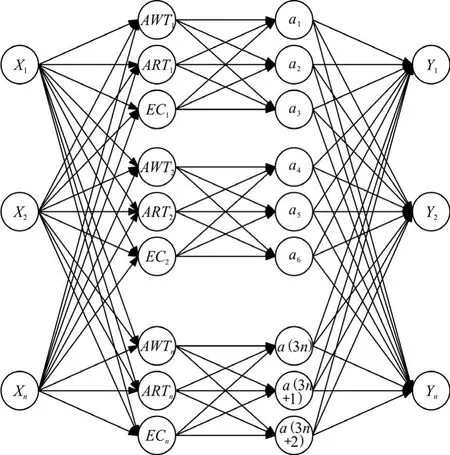
图1 四层神经网络结构示意图

3.2 隶属度函数推导

为了实现电梯的平均乘梯时间、平均候梯时间、整体能耗［8］最少，采用隶属函数来综合评估以上三个数据，建立的函数关系可以是多种，如式（1）所示。

但是最简单的调度方法是采用一次函数的调度原则。并且规定隶属函数最小值者即为最优调度电梯，可确定隶属度函数［9］如式（2）。

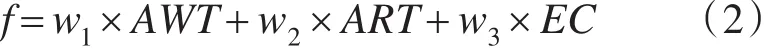
AWT、ART、EC的确定，要求不仅和当前运行状态有关，还与未来电梯运行状态有关，若采用控制器直接测定，所获取当前数据具有局限性，无法预测未来电梯运行状态特征。

间接替代法是通过测量电梯某些典型运行状态下的最长乘梯时间、最长候梯时间，以及电梯的平均乘梯时间、平均候梯时间，然后进行灰色系统预测，得到更多的电梯运行状态数据。表1为所获取电梯典型运行状态下状态量，表2为灰色系统［10］预测状态量。

选择最长乘梯时间、最长候梯时间、启停次数的原因是为了使编程简化，并且它们与平均乘梯时间、平均候梯时间、整体能耗存在内部联系。

首先我们要根据电梯最长候梯时间与电梯状态量的关系如式（3）所示。

其中a为最长候梯时间ti为单位起停时间，cl为电梯运行到结束当前待分配外呼的启停次数。tj为单位楼层运行时间，pl为每响应一次外呼电梯的运行楼层数。

平均候梯时间与电梯运行状态关系如式（4）。

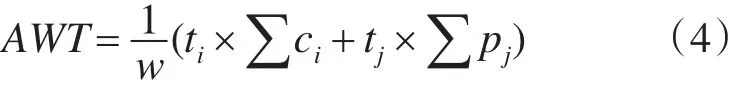
ci为从电梯运行到结束当前待分配外呼的每一次的启停次数，pj为最长运行楼层数，w为电梯外呼数量。

由上两组公式可以得出，电梯的平均候梯时间与最长候梯时间之间存在关系，根据实际研究对象的功能性能测试，便可以求出两者关系，并且符合一个长期的预测功能。

根据灰色系统预测状态量数值即最长候梯时间与其对应的平均乘梯时间，利用Matlab中的cftool工具箱［11］即可求解平均候梯时间AWT与当前的最长候梯时间a关系如式（5）所示。

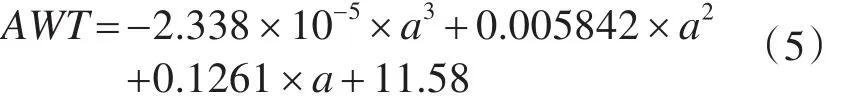
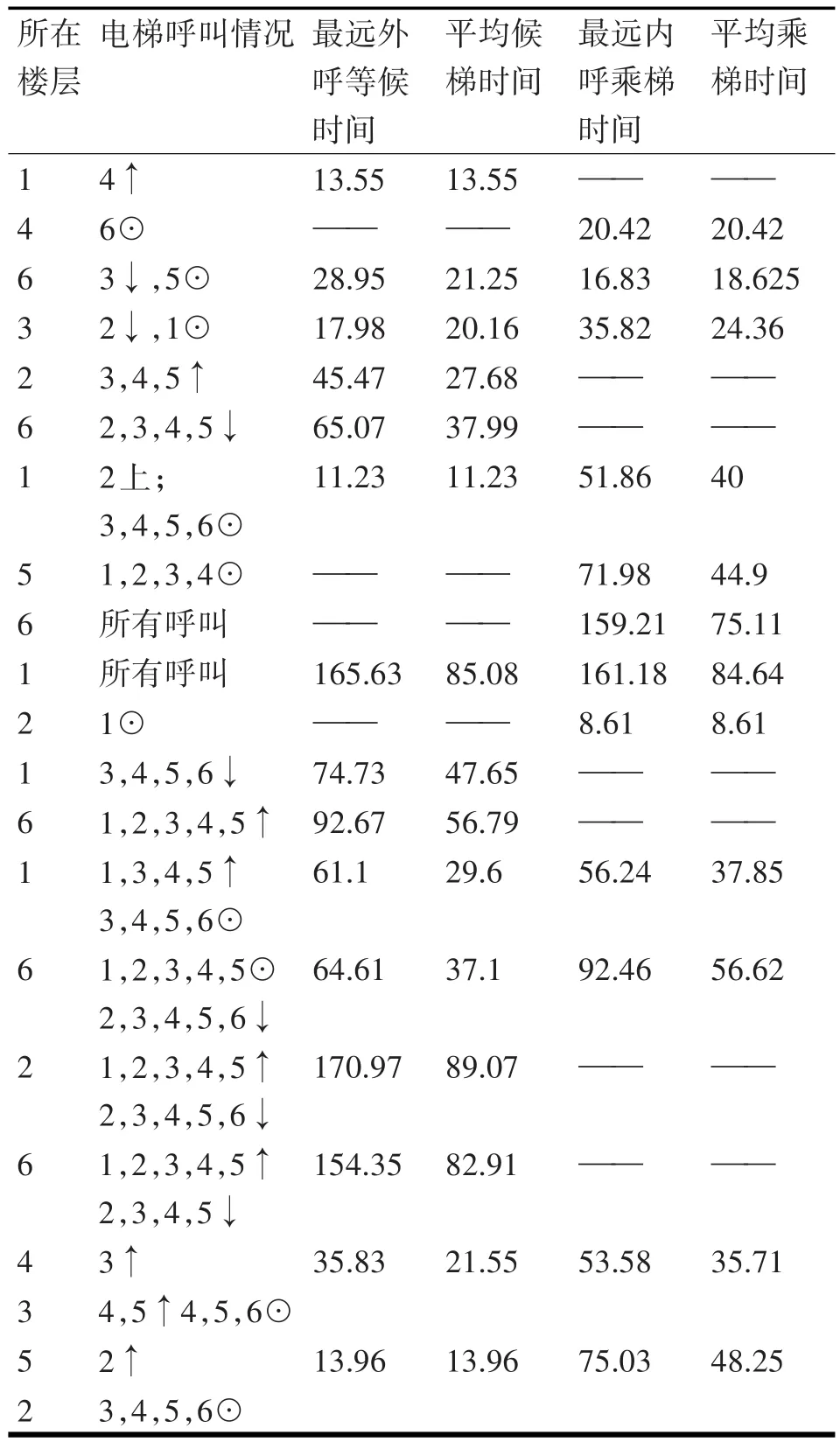
表1 单部电梯典型运行电梯状态量

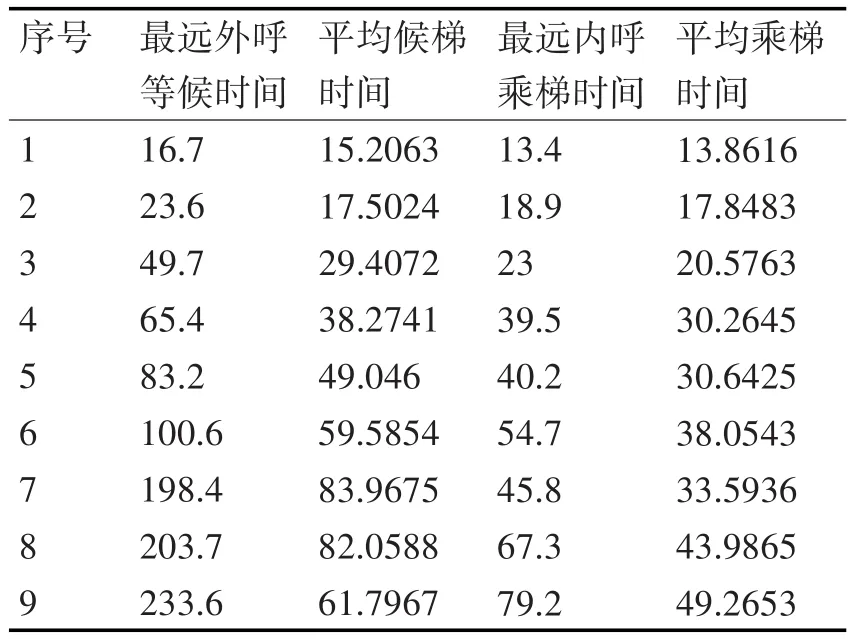
表2 灰色系统预测电梯状态量

电梯的最长乘梯时间与电梯运行参量的关系如式（6）所示。

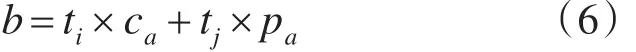
其中ca为最后一个内呼信号响应结束后的启停次数，pa为最后一个内呼信号响应结束后经历的楼层数。

电梯的平均乘梯时间与电梯运行参量关系如式（7）所示。

cai为电梯运行到每一次内呼信号响应的启停次数，paj为每次响应完内呼的电梯的运行楼层数。

由此可知，电梯平均乘梯时间可由电梯最长乘梯时间决定，针对研究的对象进行参数测试，可根据表1的状态量与表2的灰色系统预测值用Matlab中cftool工具箱拟合获得平均乘梯时间ART与最长乘梯时间b的关系如式（8）所示。

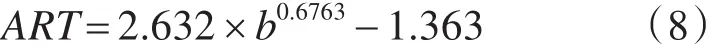
3.3 权重求解

式（1）中 w1、w2、w3权重求解，需要利用模糊神经网络求出每部电梯的隶属度函数值，再反向推倒求解平均候梯时间、平均乘梯时间、总的启停次数所占隶属度函数中权重。

通过表3模糊规则表和图2隶属度函数规则，确定的神经网络联系，最终得出的隶属度函数值。具体过程如下：

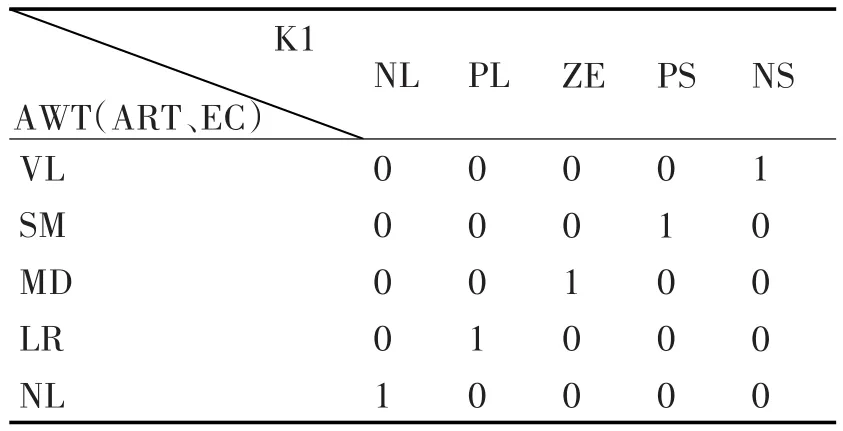
表3 模糊规则表

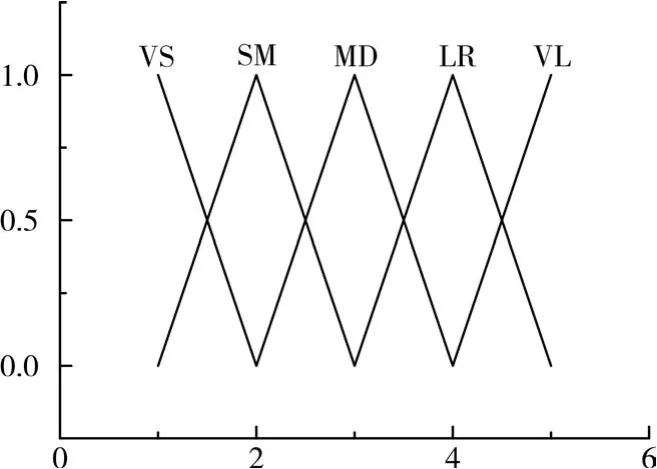
图2 电梯隶属度函数规则

将所有计算出来的AWT，ART，EC输入到神经网络系统中，在神经网络系统中建立联系，然后经过模糊规则的运算后，得到 k1，k2，k3，得到最终的隶属度函数的值为k=k1+k2+k3。利用k与输入的AWT，ART，EC进行多目标关系求解，即将多组k、AWT、ART、EC带入到上述关系式中，反推获得w1、w2、w3。

4 四层模糊神经网络的电梯群控算法验证

为检验电梯的隶属函数求解的正确性，随机选取电梯运行的状态，并与隶属度函数中的AWT、ART做误差统计分析，结果如图3、图4所示，验证了算法指标的正确性。

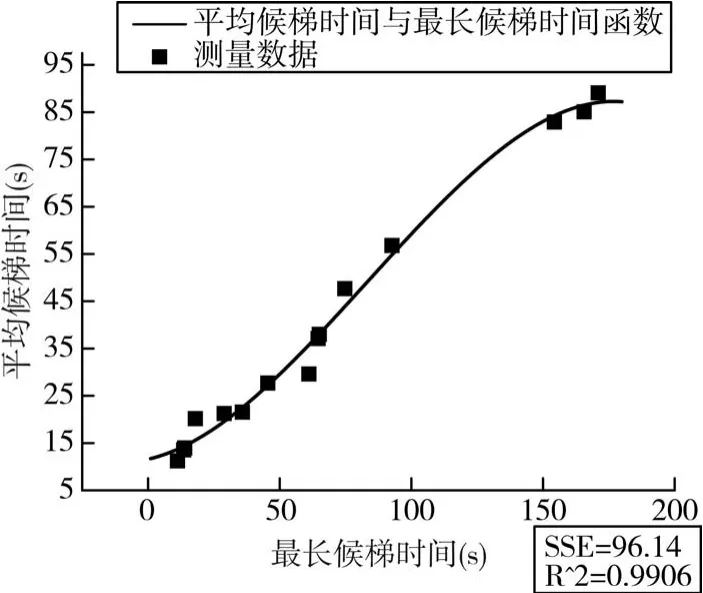
图3 AWT误差统计分析图

关于隶属度函数应用于两部6层电梯验证情况如表4所示，由调度结果可验证隶属函数的最优性。

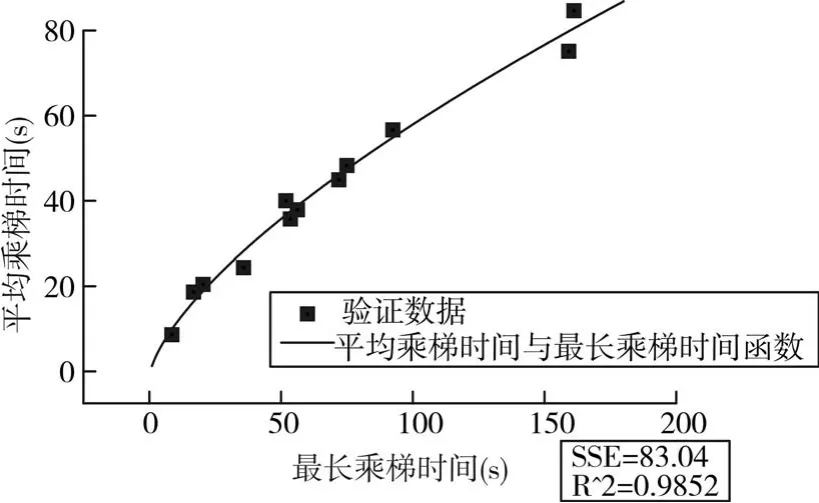
图4 ART误差统计分析图

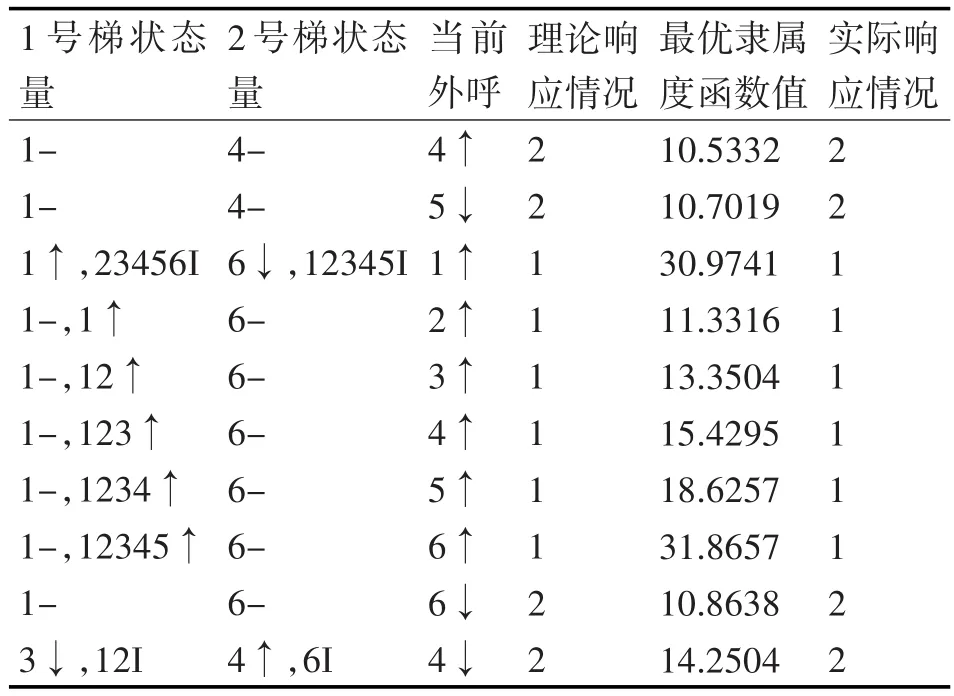
表4 三部六层电梯调度结果验证

5 PLC程序实现

5.1 面向对象结构化编程

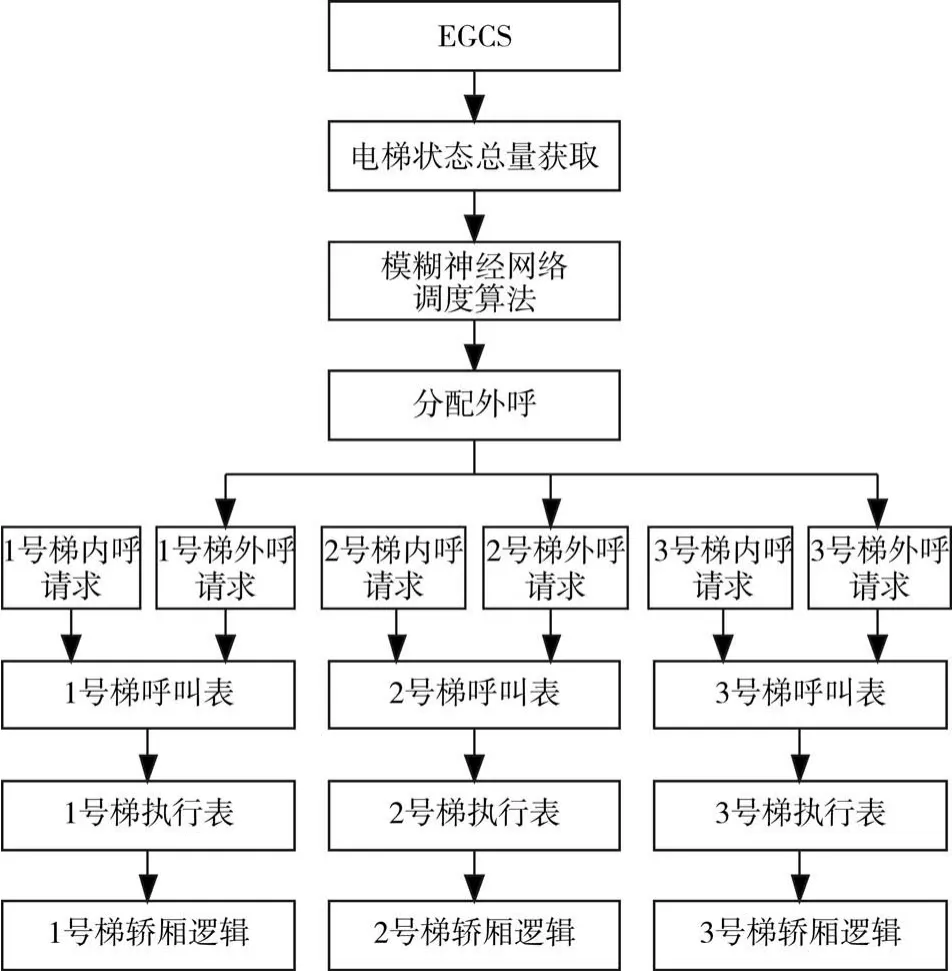
图5 三部电梯群控结构框图

多部电梯群控采用结构化编程方式［12］实现：先采用面向对象编程方式［13］实现单步电梯轿厢逻辑，包括上下行、开关门、加减速等控制，单步电梯轿厢逻辑可复用至多部电梯；进一步开放每部电梯的呼叫表，包括上行外呼表，下行外呼表，内呼叫表，呼叫表记录每一楼层的呼叫信息，通过呼叫表可生成轿厢上执行表，下执行表；最后通过模糊神经网络算法计算出最优分配后，以外呼请求形式更新至对应电梯呼叫表。PLC程序结构如图5所示。

5.2 状态总量求解

隶属度函数求解前提是获取电梯状态总量，状态总量计算复杂且计算量大，需要进行穷举推算，通过构造可变响应闭环的形式，可发挥PLC［14］运算优势，提高效率。

5.2.1 可变响应闭环

电梯响应完所有呼叫最大的运行轨迹可定义为一个完整的闭合圆环，即最大响应闭环。最大响应闭环是以轿厢当前所在楼层为闭环起点和终点，上行状态则闭环方向为：起点→上顶点→下顶点→终点，下行状态：起点-下顶点-上顶点-终点。

通过五表（上行外呼表，下行外呼表，内呼叫表、上执行表，下执行表）求出当前电梯所有呼叫中最高层的呼叫和最底层的呼叫，作为闭环上顶点和下顶点，判断出闭环的长度。

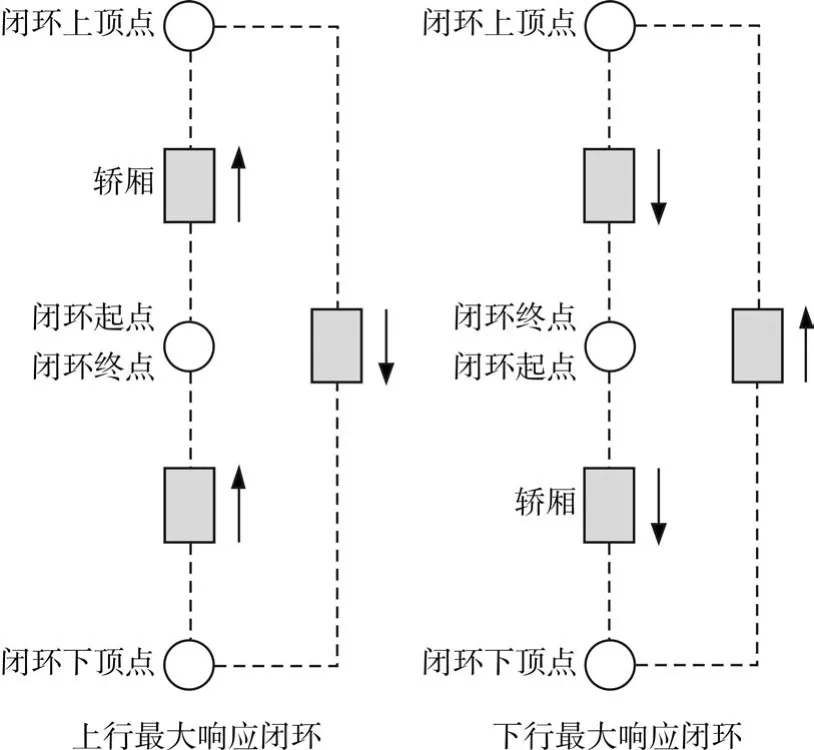
图6 可变响应闭环示例

大多情况轿厢运行不是一个完整的闭合轨迹，闭环起点和终点位于不同位置。这里仍然构造一个响应闭环，这个闭环是可变的，因最高层和最底层呼叫楼层而长度不同，因轿厢当前楼层不同而位置不同，响应闭环可以不闭合，甚至为一条直线。下面举例说明构造思路。

如图7左图所示，闭环结构中，当电梯处于睡眠状态，随机一个外呼，电梯响应闭环结构，运行轨迹为一条直线，响应闭环构造时将闭环下顶点，上顶点，终点置于同一点。

图7右图中，当轿厢响应到顶点时，可能会出现轿厢当前位置不属于下一个响应闭环范围，此时需以最近的路径将轿厢运行到响应闭环内。

图7 闭环结构调整特例

5.2.2 计算状态总量

当EGCS中每部电梯性能相同时，可根据响应闭环内的呼叫表计算状态总量。对响应闭环内的呼叫表按照闭环方向计算求出启停次数和运行楼层数。启停时间等于启停次数与单位启停时间的乘积，运行时间等于运行楼层数与单位楼层运行时间的乘积，启停时间与运行时间和即为响应时间，变换之后可求出AWT，ART，EC。

5.3 调度算法及结果分配

计算出每一部电梯的状态总量后，依据模糊神经网络算法计算出每一部电梯的隶属函数值［15］，然后按照规定好的规则对隶属函数值进行比较择优。

由隶属函数值比较之后得出最优的调度方案，将对应的外呼进行分配得出每一部电梯的呼叫表。每一个外呼仅能分配给一部电梯，此时分配的外呼是根据当前轿厢状态预判出最佳的运行逻辑［16］。

由于人为因素的影响，轿厢不会完全按照预判出的响应闭环运行，多部电梯在响应过程中不可避免地会发生响应冲突，为解决冲突问题，采用更新呼叫表机制。EGCS的外部呼叫总表包含每一部电梯自身的外呼叫表，分配机制采用每一个呼叫只会分配给一部电梯，冲突现象会反映到呼叫总表上，用呼叫总表更新每一部电梯的呼叫表可以有效发现并且解决冲突现象。

6 结语

通过对实际电梯对象的研究，根据具体电梯进行模糊规则定义与网络建立，计算出电梯的实际隶属函数，通过Matlab仿真测试与实际情况检验，验证结果说明电梯调度原则的准确性。提出基于PLC的可变闭环编程方式实现调度机制，降低了算法实现难度。根据上述模糊神经网络调度规则的机制增强了对不同EGCS性质的针对性，能够实现任意系统的调度。

同时，本文所提出的四层模糊神经网络可以应用于以下建模与仿真应用，用以解决有针对性的工程应用实例，减小成本误差。

1）实现n部n层电梯调度，解决电梯层数已知条件下编程的局限性。

2）对于任意系统内部相关联，内部变量关系未知，系统具有特殊性。利于预测规划系统状态。

3）优化编程实现过程，减小编程难度。

［1］陈步荣.基于改进遗传算法的电梯群控系统设计及仿真系统开发［D］.南京：南京航空航天大学，2007.

CHEN Burong.Development of elevator group control sys⁃tem design and simulation system based on improved ge⁃netic algorithm［D］.Nanjing：Nanjing University of Aero⁃nautics and Astronautics，2007.

［2］唐应辉，唐小我.排队论基础与分析技术［M］.北京：科学出版社，2006：23-41.

TANG Yinghui，TANG Xiaowo.Queuing theory and analy⁃sis technology［M］.Beijing：Science Press，2006：23-41.

［3］朱德文，杨祯山，张筠莉.智能控制电梯工程系统［M］.北京：中国电力出版社，2007：46-51.

ZHU Dewen，YANG Zhenshan，ZHANG Junli.Intelligent Control of Elevator Engineering System［M］.Beijing：Chi⁃na Electric Power Press，2007：46-51.

［4］吴蕾.基于神经网络的电梯群控系统智能调度的研究［D］.武汉：武汉理工大学，2007.

WU Lei.Research on intelligent dispatch of elevator group control system based on neural network［D］.Wuhan：Wu⁃han University of Technology，2007.

［5］朱德文，付国江.电梯群控技术［M］.北京：中国电力出版社，2006：19-88.

ZHU Dewen，FU Guojiang.Elevator group control technol⁃ogy［M］.Beijing：China Electric Power Press，2006：19-88.

［6］Markon S，KitaH，Nishikawa Y.Adaptive Optimal Eleva⁃tor Group Control by Use of Neural Networks［J］.Trans of the Institute of System’s Control and Information Engineer，1994，7（12）：487-497.

［7］邓宗明.模糊神经网络技术在电梯群调度中的应用［D］.桂林：广西师范大学，2001.

DENG Zongming.Application of fuzzy neural network in elevator group dispatching［D］.Guilin：Guangxi Normal University，2001.

［8］Jianzhe Tai，Suying Yang，Hong Tan.Dispatching Ap⁃proach Optimization of Elevator Group Control System with Destination Floor Guidance using Fuzzy Neural Net⁃work［C］//Proceedings of the 7thWorld Congress on Intel⁃ligent Control and Automation，Chongqing，China，June 25-27，2008.Chong qing：World Congress on Intelligent Control&Automation，2008：7085-7088.

［9］沈海蛟.基于模糊控制的电梯群控系统研究［D］.锦州：辽宁工业大学，2014.

SHEN Haijiao.Study on elevator group control system based on fuzzy control［D］.Jinzhou：Liaoning University of Technology，2014.

［10］司守奎，孙兆亮.数学建模算法与应用［M］.北京：国防工业出版社，2015：67-89.

Secretary Shoukui，SUN Zhaoliang.Mathematical model⁃ing algorithm and application［M］.Beijing：National De⁃fense Industry Press，2015：67-89.

［11］卓金武.MATLAB在数学建模中的应用［M］.北京：北京航空航天大学出版社，2011：56-68.

ZHUO Jinwu.MATLAB application in mathematical modeling［M］.Beijing：Beijing University of Aeronautics and Astronautics Press，2011：56-68.

［12］朱文杰.S7-1200 PLC编程与应用.第一版［M］.北京：中国电力出版社，2015：169-319.

ZHU Wenjie.Programming and Application of S7-1200 PLC.First Edition［M］.Beijing：China Electric Power Press，2015：169-319.

［13］崔坚.TIA博图软件STEP7 V11编程指南.第一版［M］.北京：机械工业出版社，2012：66-318.

CUI Jian.TIA Plot Software STEP7 V11 Programming Guide.First Edition［M］.Beijing：Mechanical Industry Press，2012：66-318.

［14］张炜炜.基于PLC技术的群控电梯主从站设计［D］.南京：南京理工大学，2012.

ZHANG Weiwei.Design of group-controlled elevator master-slave based on PLC technology［D］.Nanjing：Nanjing University of Science and Technology，2012.

［15］岳庆来.电梯现代智能控制技术［M］.北京：机械工业出版社，2009：220-239.

YUE Qinglai.Modern Intelligent Control Technology of Elevator［M］.Beijing：Mechanical Industry Press，2009：220-239.

［16］张福恩，吴乃优，张金陵，等.交流调速电梯原理、设计及安装维修［M］.北京：机械工业出版社，1993：9-84.

ZHANG Fuen，WU Naiyou，ZHANG Jinling，et al.The principle，design，installation and maintenance of AC variable speed elevator［M］.Beijing：Mechanical Indus⁃try Press，1993：9-84.

［17］刘载文，李惠升，钟亚林.电梯控制系统［M］//继电器与PC控制原理、设计及调试.北京：电子工业出版社，1996：18-254.

LIU Zaiwen，LI Huisheng，ZHONG Yalin.Elevator con⁃trol system［M］//Relay and PC control principle，design and debugging.Beijing：Publishing House of Electronics Industry，1996：18-254.

Elevator Group Control A lgorithm Research and Control Program Im p lementation Based on Fuzzy Neural Network w ith Four-layer Structure

XU Yingjie1PAN Tingzhe1HU Zhinan2HUANG Jingshan1
（1.School of Aerospace Engineering，Xiamen University，Xiamen 361005）（2.College of Physical Science and Technology，Xiamen University，Xiamen 361005）

TP301.6

10.3969/j.issn.1672-9722.2017.09.015

2017年3月3日，

2017年4月5日

青年科学基金项目“发展适用于肿瘤细胞实时快速拉曼成像的光谱信号处理方法”（编号：21503171）资助。

许英杰，男，硕士，工程师，研究方向：工业控制，电子电路。潘廷哲，男，研究方向：电机控制，嵌入式开发。胡志男，女，研究方向：电子信息科学与技术，电子电路。黄景山，男，研究方向：机械装备，智能制造。