基于滑模理论的四旋翼飞行器轨迹跟踪控制∗

杨建华

基于滑模理论的四旋翼飞行器轨迹跟踪控制∗

杨建华

（西安工业大学电子信息工程学院 西安 710072）

针对四旋翼飞行器控制系统强耦合、复杂非线性、欠驱动的特点，提出一种采用双环控制结构的高精度轨迹跟踪滑模控制器，外环实现位置跟踪控制，内环实现姿态跟踪控制。在位置子系统中，对质量负载和外界干扰进行自适应估计。利用李亚普诺夫稳定性理论证明了该系统的收敛性和稳定性。仿真实验结果表明该控制系统具有较强的稳定性和鲁棒性。

四旋翼飞行器；滑模控制；位置跟踪；鲁棒性

AbstractAccording to the characteristics of the Quadrotor Helicopter control system —strong coupling，complex nonlinear，under-actuated，a trajectory tracking sliding mode controller using inner and outer loop structure with high accuracy is proposed.Outer ring is to realize position tracking control while the inner ring is to realize the attitude tracking control.In the position control subsystem，the external interference and mass of system are adaptively estimated.The stability and convergence characteristics are proved by constructing Lyapunov function.The simulation results show that the control system has strong robustness and stability.

Key Wordsquadrotor helicopter，sliding mode control，position tracking，robustness

Class NumberTP391

1 引言

四旋翼飞行器是一种具有6个自由度和4个控制输入的可垂直起降、悬停、前飞、侧飞和倒飞的无人驾驶飞行器，4只旋翼可相互抵消反扭力矩，不需要专门的反扭矩桨。被广泛应用于无人侦察、森林防火、灾情监测、城市巡逻等领域［1～2］。飞行控制系统是四旋翼飞行器的核心部分，其性能的好坏决定了整个系统的性能。近年来，微小型四旋翼无人机的自主飞行控制得到了研究人员的广泛关注。四旋翼飞行器姿态运动模型具有强非线性、强耦合性和欠驱动的特点，这给系统精确的鲁棒控制提出了很高的要求［3］。同时，四旋翼飞行器由于其自身构造的特点造成了其易于受外界干扰与自身扰动影响的特点，这也增加了控制上的难度［4～5］。目前，国内外研究机构针对以上问题设计的飞行控制方法主要有PID控制、改进的PID控制、Backstepping控制、滑模变结构控制、神经网络控制、模糊控制等［5～8］。由于滑模控制具有响应速度快、对参数变化及扰动不敏感、无需系统在线辨识、物理实现简单等优点，近年来受到了广泛的关注［9～10］。

本文针对四旋翼飞行器控制系统强耦合、复杂非线性、易受外界干扰的特点，采用内外环控制的控制方法来设计控制律，达到消除参数的不确定性和外加干扰的目的，保证了系统的稳定性。其中，外环为位置环，内环为姿态环。为了实现四旋翼飞行器的高精度轨迹跟踪，在位置子系统中，采用虚拟滑模控制输入，并对质量负载和外界干扰进行自适应估计。数值仿真实验结果表明，该控制方法具有较高的精度，能够使飞行器较好地跟踪飞行目标的期望值，具有良好的鲁棒性。

2 四旋翼飞行器动力学模型

为了研究四旋翼飞行器的空间运动规律，首先需要建立合适的坐标系，一般四旋翼飞行器的坐标系分为载体坐标系和固定坐标系。如图1所示，以OE为地面坐标系原点，建立OXYZ坐标系，以OB为飞行器质心，建立Oxyz为飞行器的载体坐标系，两者都是右手坐标系。对于飞行器姿态描述采用欧拉角表示方法。其中俯仰角φ，横滚角θ，航向角ψ作为飞行器的姿态角，俯仰角φ定义为机体x轴与地面坐标系X轴的夹角；横滚角θ定义为机体y轴与地面坐标系Y轴的夹角；航向角ψ定义为机体z轴与地面坐标系Z轴的夹角。

图1 地面与机体坐标系

为了建立四旋翼飞行器的动力学模型，需满足如下假设：

1）刚体坐标系原点OB和四旋翼飞行器的质心重合。

2）刚体坐标系 B{Bx，By，Bz} 和惯性坐标系J{Ex，Ey，Ez}各个轴重合。

3）外界干扰力和质量为慢时变信号。

四旋翼飞行器的动力学模型如下：

其中，m为负载总质量，P=[x ， y，z]T为飞行器在惯性坐标系中质心的位置，U1和为系统的中间控制输入，e3=[0 0 1]T为竖直方向的单位向量，dF=[dxdydz]T和dΓ=[dφdθdψ]T分别代表气流对四旋翼飞行器的干扰力和干扰力矩。Θ=[φ θ ψ]T为三个姿态的欧拉角，分别代表滚转角、俯仰角和偏航角；R为从刚体坐标系到惯性坐标系之间的转换关系，表达式如下

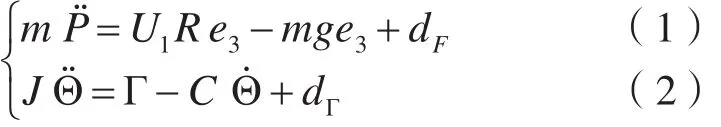
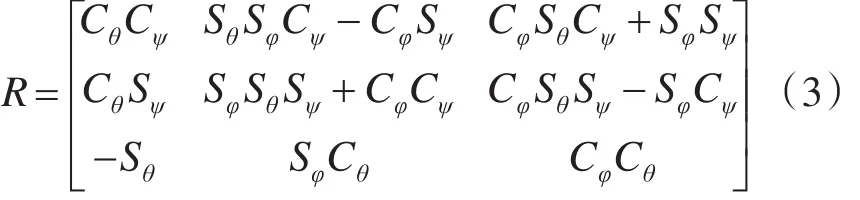
其中，S(·)和C(·)分别代表正弦和余弦函数。J是刚体惯性张量I=[IxxIyyIzz]T在惯性坐标系中的表示：

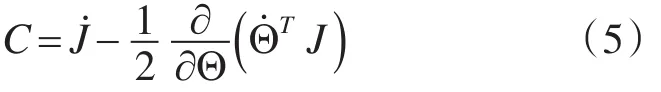
由式（4）和式（5）可解得科里奥力及离心力项C。

科里奥力及离心力项C可由下面的式子计算得到：

螺旋桨转速ω与四个螺旋桨产生的总升力的关系为进一步得到螺旋桨的姿态控制输入转矩：

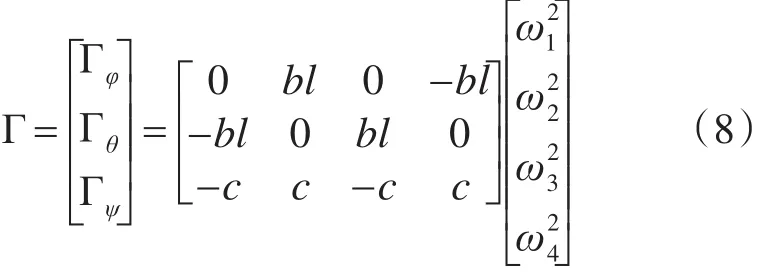
其中，b、c均为与空气动力学相关的常数，l为四旋翼飞行器的配置半径。

3 轨迹跟踪控制器的设计

3.1 位置跟踪控制器设计

假设飞行器在期望空间运动状态有界：

ηd为期望轨迹，ηd为正常数。状态向量ηd可观测，至少一阶可微。定义跟踪误差为eη=η-ηd，则由式（1）可得位置子系统的跟踪误差方程为

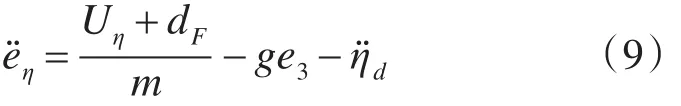
其中，Uη=U1R e3为待设计的虚拟控制输入，U1为实际的升力。定义滑模函数如下：

考虑到四旋翼飞行器负载质量和外部干扰的不确定性，设计位置虚拟控制律UP为

其中

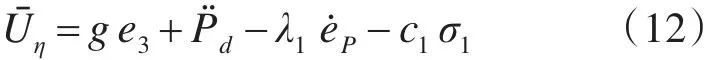
其中，c1＞0，m̂和d̂F分别代表质量和外界干扰的估计值。

设计自适应律为

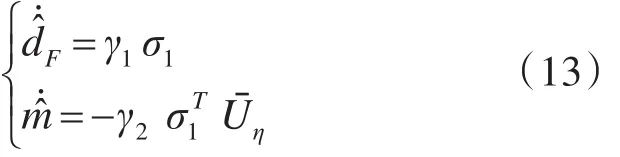
定义干扰估计误差 d͂F=dF-d̂F，质量估计误差 m͂=m-m̂。

为了保证控制系统的稳定性和收敛性，定义Lyapunov函数为

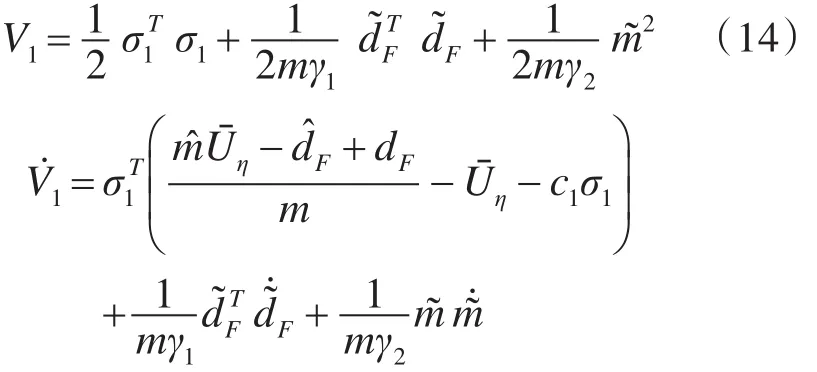
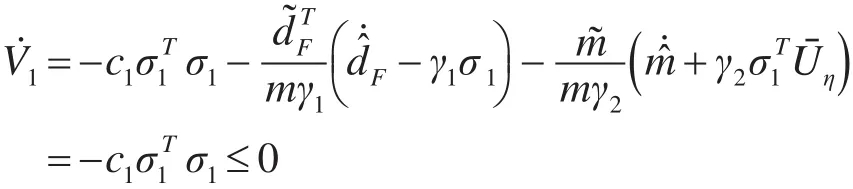
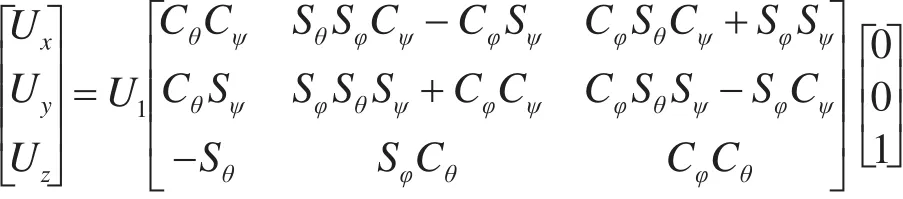
展开联立解得俯仰角度指令信号为

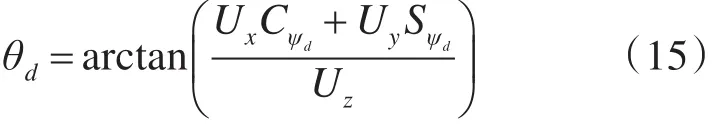
滚转角度指令信号为

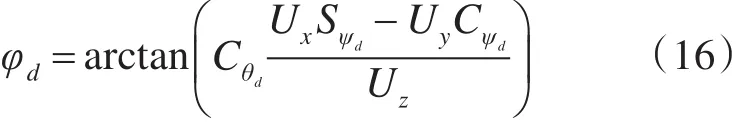
由Uz=U1CφCθ及式（15）和式（16）可得实际的位置控制输入为

由于四旋翼飞行器为典型的欠驱动控制系统，控制器不可能对其6个自由度都进行跟踪，这里跟踪其位置P=[x y z]T和偏航角ψd，同时完成滚转角φd和俯仰角θd的镇定。

3.2 基于干扰观测器的姿态跟踪控制器设计

3.2.1 干扰观测器设计

位置子系统中对U1进行了设计，使其能精确地跟踪位置η，同样，为了跟踪中间指令信号Θd，也需要对控制输入转矩Γ进行设计。将式（2）写成如下形式：

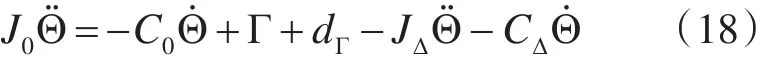
其中，J=J0+JΔ，C=C0+CΔ。令 d1=dΓ-JΔΘ̈-CΔΘ̇，其中，‖‖d1≤D1。

则有：

其中，d̂1为干扰估计值，K＞0 ，且 ḋ1=0 。并令观测误差为：d͂1=d1-d̂1。

干扰观测器设计为：

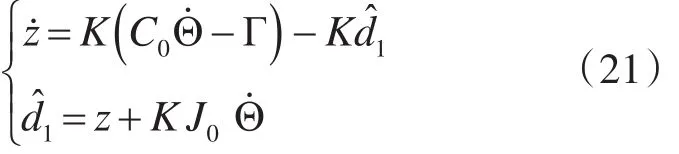
则：

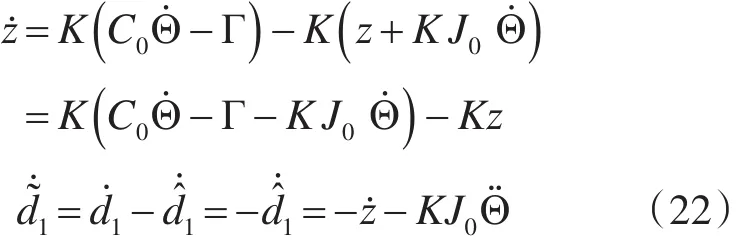
由 ż和式（22）得：

从而得到干扰观测器的误差方程：

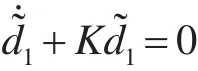
参数K决定该干扰观测器的收敛精度。

3.2.2 姿态滑模控制器设计

采用干扰观测器式（21）观测干扰d1，在滑模控制中对干扰进行补偿，从而降低切换增益，进而降低抖振。

其中 λ2＞0，eΘ=Θd-Θ，则有：

对输入转矩取控制律：

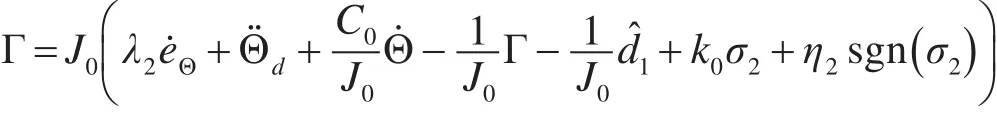
其中，k0＞0。代入得：

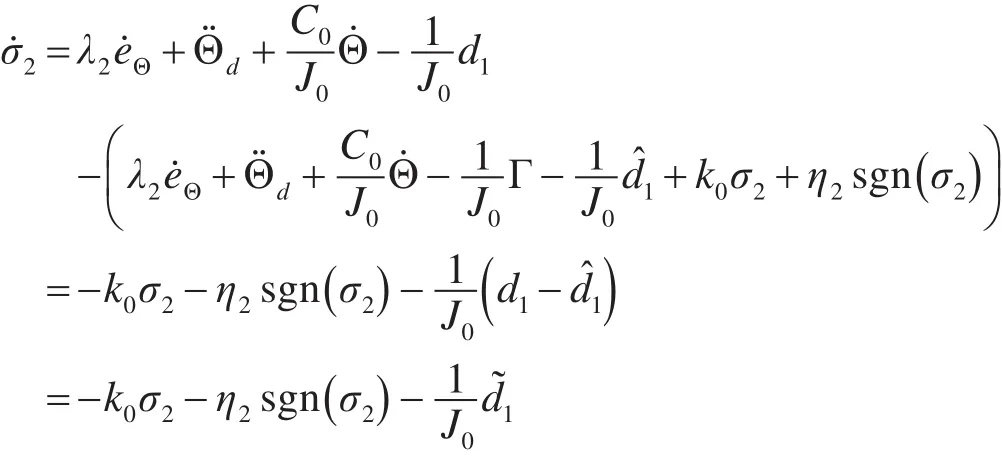
取闭环系统的Lyapunov函数为

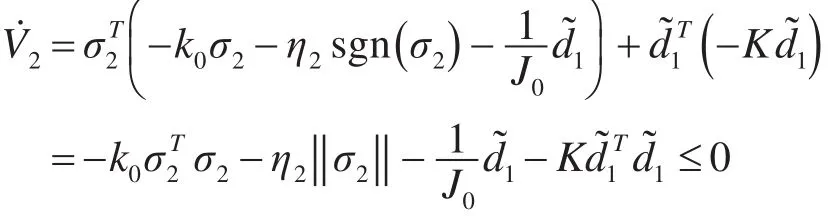
4 系统仿真结果与分析

根据以上建立的动力学模型和控制系统，本文采用Matlab SIMULINK对水下机器人跟踪期望轨迹进行了仿真分析。

假设期望跟踪的参考位置为

飞行器的配置半径为l=0.4m，仿真时间为50s，位置跟踪控制器参数为 c1=5，λ1=diag(3 3 3) ，γ1=4 ， γ2=0.2 姿态子系统参数为，η2=0.2 ， λ2=diag[3 0 30 30]。仿真结果如图2～图4所示。

从图2～图4可以看出，飞行器飞行轨迹能够快速跟踪参考位置目标，基本在2s内完成位置和姿态的跟踪。Y轴跟踪出现轻微振荡后，逐渐稳定跟踪到参考目标。

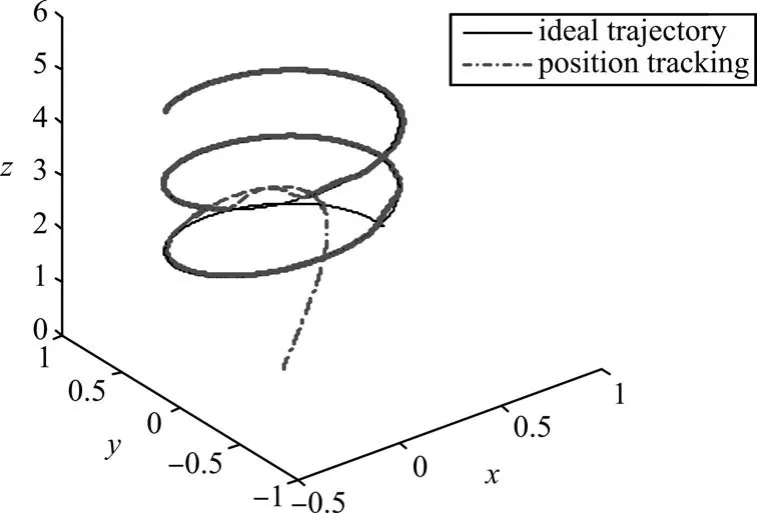
图2 飞行器三维跟踪效果

图3 位置跟踪误差

5 结语

针对四旋翼飞行器控制系统强耦合、复杂非线性、欠驱动的特点，设计了一种内外环控制的高精度轨迹跟踪及质量自适应的控制系统，该系统能够在负荷质量不确定且外部干扰不确定时较好地跟踪设定目标。仿真结果表明该系统具有良好的稳定性和鲁棒性。

［1］杨柳，刘金琨.基于干扰观测器的四旋翼轨迹跟踪鲁棒控制［J］.飞行力学，2015，33（4）：1-6.

YANG Liu，LIU Jinkun.Disturbance observer-based ro⁃bust trajectory tracking control for a quadrotor UAV［J］.

Flight Dynamics，2015，33（4）：1-6.

［2］宿敬亚，樊鹏辉，蔡开元.四旋翼飞行器的非线性PID姿态控制［J］.北京航空航天大学学报，2011，37（9）：1054-1058.

SU Jingya，FAN Penghui，CAI Kaiyuan.Attitude control ofquadrotor aircraft via nonlinear PID［J］.Journal of Bei-jing University of Aeronautics and Astronautics，2011，37（9）：1054-1058.

［3］宁国栋，张曙光，方振平，等.RLV再入初期连续滑模姿态控制律设计及仿真［J］.系统仿真学报，2007，19（22）：5272-5276.

NING Guodong，ZHANG Shuguang，FANG Zhenping，et al.Attitude Control via Continuous Sliding Modes for RLV Initial Reentry［J］.Journal of System Simulation，2007，19（22）：5272-5276.

［4］刘金琨.滑模变结构控制Matlab仿真［M］.北京：清华大学出版社，2005.

LIU Jinkun.Sliding Variable Structure Control Matlab Simulation［M］.Beijing：Tsinghua UniversityPress，2005.

［5］Zhang R，Quan Q，Cai K Y.Attitude control of a quadro⁃tor aircraft subject to a class of time-varying disturbances［J］.IET Control Theory Applications，2011，5（9）：1140-1146.

［6］李瑞琪，王洪福，李瑞雪，等.基于模型参考自适应的四旋翼飞行器控制［J］.计算机测量与控制，2013，21（12）：3260-3263.

LI Ruiqi，WANG Hongfu，LI Ruixue，et al.Controlling Quadrotor Vehicles Based on Model Reference Adaptation Contrl［J］.Computer Measurement&Control，2013，21（12）：3260-3263.

［7］KIM Jinhyun，KANGMinsung，PARK Sangdeok.Accurate modeling and robust hovering control for a Quadrotor VTOL aircraft［J］.Journal of Intelligent and Robotic Sys⁃tems，2010，57：9-26.

［8］Dierks T，Jagannathan S.Output feedback control of a quadrotor UAV using neural networks［J］.IEEE Trans Neural Networks，2010，21（1）：23-50.

［9］甄红涛，齐晓慧，李杰，等.四旋翼无人机L1自适应块控反步姿态控制器设计［J］.控制与决策，2014（6）：1076-1082.

ZHEN Hongtao，QI Xiaohui，LI Jie，et al.Quadrotor UAV L1 adaptive block backstepping attitude controller［J］.Control and Decision，2014（6）：1076-1082.

［10］Abdessameud A.Tayebi A.Global Trajectory Tracking Control of VTOL-UAVs without Linear Velocity Mea⁃surements［J］.Automatica，2010，46（6）：1053-1059.

Trajectory Tracking Control for a Quadrotor UAV Based on Sliding M ode Theory

YANG Jianhua
（School of Electronic Information Engineering，Xi’an Technological University，Xi’an 710072）

TP391

10.3969/j.issn.1672-9722.2017.09.011

2017年4月17日，

2017年5月21日

陕西省教育厅专项科研计划项目（编号：16JK1372）；国家自然基金项目“深海空间站回转型穿梭器网络化控制性能分析与优化”（编号：61473224）资助。

杨建华，男，讲师，博士研究生，研究方向：控制理论与控制工程，电子技术应用。