STMV波束形成算法并行处理实现方法研究∗

周亦军 刘千里

STMV波束形成算法并行处理实现方法研究∗

周亦军 刘千里

（海军驻武汉四三八厂军事代表室 武汉 430060）

在讨论了STMV（导向最小方差）波束形成算法原理的基础上，提出了STMV波束形成算法的逆QR（正交分解）分解SMI（采样矩阵求逆）实现方法，讨论了逆QR分解SMI算法的Systolic阵列并行实现结构，分析组成Systolic阵列的各PE（处理单元）单元的基本运算模块的实现，并研究了逆QR分解SMI算法基于Systolic阵列结构的FPGA（现场可编程门阵列）并行实现方法。

导向最小方差；采样矩阵求逆；波束形成；Systolic阵列；FPGA

AbstractOn the basis of discussing STMV（steered minimum variance）beam-forming algorithm principle，the implementa⁃tion method of STMV beam-forming algorithm with inverse QR（orthogonal decomposition）into the SMI（sample matrix inver⁃sion）is proposed.The Systolic array parallel structure of inverse QR decomposition of the SMI algorithm has been discussed.The composition of Systolic array each PE（processing unit）basic operations module is analyzed.Inverse QR decomposition of the SMI algorithm is based on the Systolic array structure of the FPGA（field programmable gate array）parallel implementation method.

Key WordsSTMV，SMI，beam-forming，Systolic array，FPGA

Class NumberTP23

1 引言

随着人们对水声传播原理认识的深入和各种新的信号处理算法在声纳中的应用，声纳逐渐向宽带、低频、远距离或是近场、高频、高分辨率等方向发展［1］。由于这些新的信号处理方法或技术通常需要的运算量大幅增加，且算法结构一般也比较复杂。为了使这些新方法能够在声纳系统中得以实时实现，需要开发高速并行处理系统和设计相应的并行计算方法。

空间谱估计在声呐、雷达、通信等领域具有重要意义。最早的空间谱估计方法常规波束形成（conventional beam-forming，CBF）的方位分辨力由瑞利限决定［2］。为了提高方位分辨力，Capon提出了最小方差无畸变波束形成方法（minimum vari⁃ance distortion less response，MVDR）［3］。处理宽带信号时，MVDR将宽带分成若干频点，在每个频点上估计空间谱，相加得到宽带结果，这是非相干累积，因此会损失信息，处理相干源时方位分辨能力下降，而且需要不少于阵元数的快拍数才能达到收敛。针对这些问题，Krolik和Swingler提出了导向最小方差波束形成（steered minimum variance，ST⁃MV）［4］。STMV是基于导向协方差矩阵（steered co⁃variance matrix，STCM）对不同频点的互谱密度矩阵进行相干积累，计算宽带空间谱。STMV可以获得宽带增益并减少收敛时间，并且能直接处理相干源。

任何数字信号处理算法的实用性归根到底取决于该算法在计算上的可行性［5］。本文从STMV波束形成的并行实现角度入手，在讨论了STMV波束形成算法原理的基础上，提出了STMV波束形成算法的逆QR（正交分解）分解SMI（采样矩阵求逆）的实现方法，讨论了逆QR分解SMI算法的Systolic阵列并行实现结构，分析组成Systolic阵列的各PE单元的基本运算模块的实现，并研究逆QR分解SMI算法基于Systolic阵列结构的FPGA并行实现方法。

2 STMV波束形成算法原理

文献［6］提出的一种相干波束形成算法：基于导向协方差矩阵（steered covariance matrix，STCM）的宽带导向最小方差波束形成算法（Steered Mini⁃mum Variance-STMV），其原理是通过波束旋转使指定方向θ的响应为1，而波束形成的输出能量最小。

按照常规时延求和波束形成，对每个阵元输出信号插入时延 τm(θ)=md cos(θ)/c，m=0，…，M-1，则时延后输出为

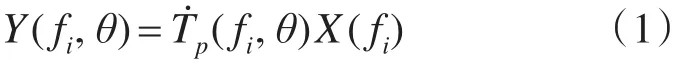
加权的时延波束形成输出为

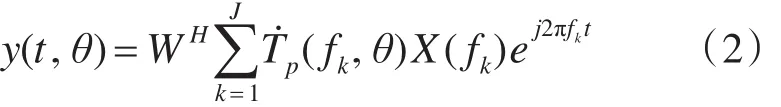
式中：W为一组权矢量。波束的功率为

当快拍的长度足够长k≠m时，X(fk)与X(fm)是不相关的，因此有：

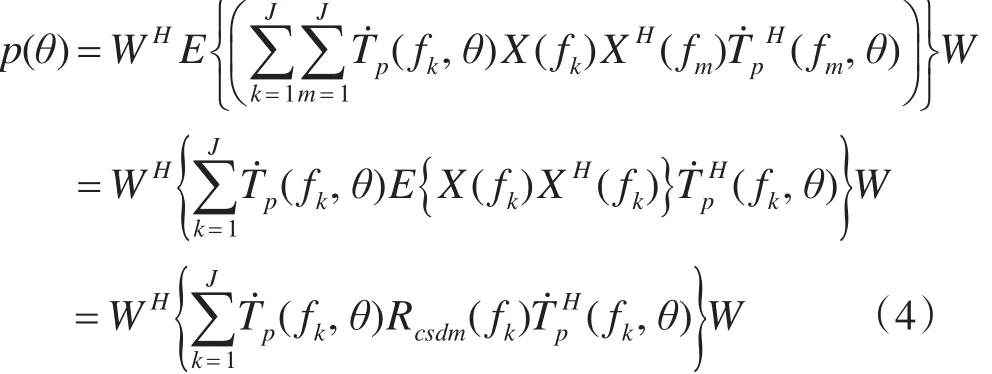
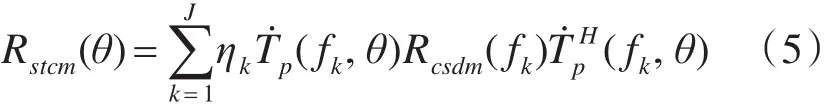
式中ηk是第k个频点的加权系数即为该频点的信噪比。

最优波束形成问题就是求权向量W使目标方向θ的响应为1，而波束输出功率式（4）最小，即

式（6）中1M表示M×1的1的向量。

导向协方差矩阵由于综合利用了各子带的信息，只要满足子带数与快拍数的乘积不小于导向协方差矩阵的维数，导向协方差矩阵就是可逆的［6］。

3 STMV算法的逆QR分解SM I实现方法

从上节分析我们知道最优波束形成问题就是求权向量W使目标方向θ的响应为1，而波束输出功率式（4）最小。下面介绍SMI算法：

线性约束最小方差（LCMV）准则可描述为

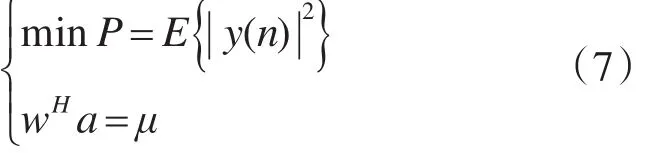
这里μ为常数，y(n)表示第n个采样时刻下的波束输出，a为期望信号导向矢量，P为功率可进一步表示为

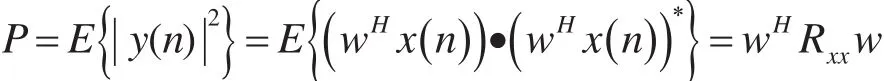
这里Rxx为输入矢量的协方差矩阵。该准则的物理意义为：在保证对有用信号的增益为常数的前提下，输出总功率最小。该准则实际上与输出信噪比最大等效。式（7）的拉格朗日解可表示为

对于在定向方向的单位增益约束（即μ=1，wHa=1），LCMV退化为最小差无失真响应（MV⁃DR）波束形成器。根据最大似然准则，采样信号矢量x的n次采样可构成Rxx的最佳估计R̂xx：

用 R̂xx代替 Rxx求解式（8）便是SMI算法。

对采样信号矢量x的n次采样Rxx作DFT转换到频域，即可得到Rcsdm(fk)，根据导向协方差矩阵定义即可求得Rstcm(θ)，由此可以采用SMI算法来求权向量W。

QR分解SMI算法需要前向和后向带入才能获得自适应权向量W［7］，这不但增加了系统的硬件规模，同时也造成了软件实现的复杂性。本文在前面论述的基础上，对算法结构进行了进一步的改进，实现了一种不需要前向后向回带的QR分解SMI算法，由于该方法用到了三角阵求逆进行推导，称之为逆QR分解SMI算法［7］。

设第 n次快拍时输入信号为x(n)=[x1(n)，x2(n)，…，xM(n)]T，设 vn=A-nHa，则可以得到n次快拍在LCMV条件下的权向量Wn：

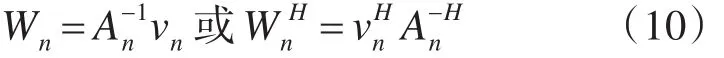
式（10）给出了另外一种自适应权向量的求解方法，即将求解Wn转换成求解下三角矩阵A-Hn和中间向量vn的问题。

下面讨论A-nH矩阵的递推更新问题。设n-1时刻已经实现输入数据矩阵的三角化，那么在n时刻存在酉阵Q(n)=GM(n) GM-1(n)…G1(n)使下式成立：

式中x(n)是n次快拍时各阵元接收数据构成的列向量，所以有：

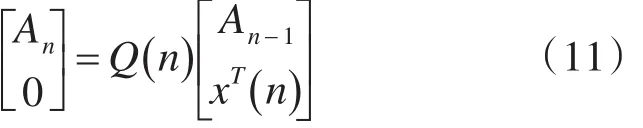
对式（11）作如下处理：

根据矩阵求逆引理，对上式两边同时求逆，有：

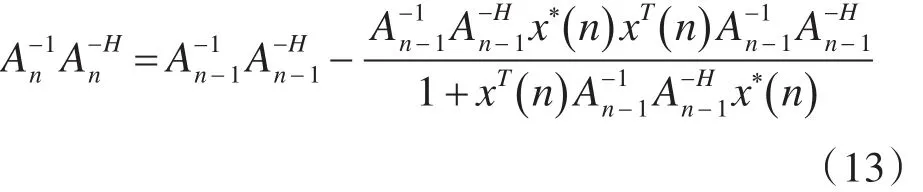
令中间变量 z(n)=A-nH-1x*(n ) ，t(n)=，上式可简化为

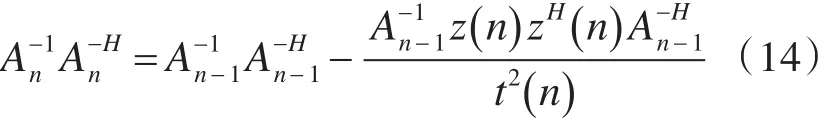
进一步，令 q(n)=A-n1-1z(n)/t(n ) ，则qH(n)=zH(n) A-nH-1/t(n)，上式可写成：

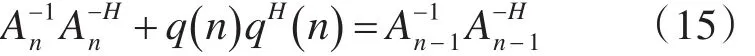
这样我们得到如下结论：必然存在一个酉阵P(n)使下式成立：

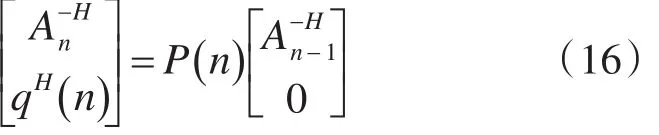
根据表达式t(n)得到t2(n)=1+zH(n) z(n)，则有下式成立：

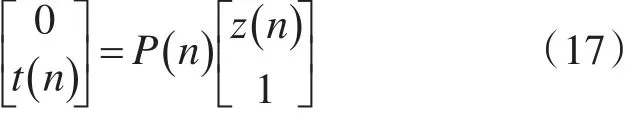
比较式（16）和式（17）可知，当一个酉矩阵通过输入1向量把z(n)变换成零向量的时候（该酉矩阵通过一系列Givens旋转产生［8］），相同的旋转变换通过输入0向量将A-nH-1更新为A-nH，由此实现矩阵的递推更新。实现了矩阵的递推更新，下面讨论另一个变量vn的更新方法。将式（15）两边同时右乘a左乘aH，经过适当的变形可得到：

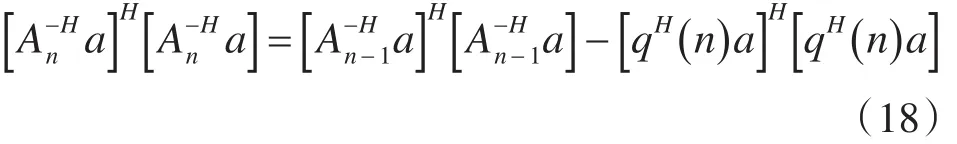
设 β(n)=qH(n) a，同时考虑到vn=A-nHa，上式可改写成：

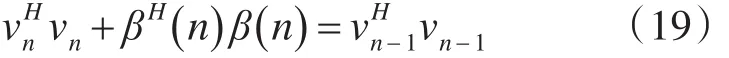
则有下式成立：

式（20）说明，相同的酉矩阵P(n)能通过输入0向量将vn-1更新为vn。

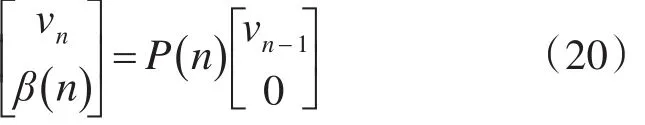
4 逆QR分解SM I算法的Systolic阵列实现

自适应波束形成中都需要大量的矩阵运算，其中矩阵分解或是求逆又是其主要工作。因此，矩阵运算往往成为自适应阵列处理系统中实时性能的瓶颈［9］。在实际应用中，SMI算法需要实时地进行数据矩阵的更新，数据矩阵更新需要相应的迭代算法与之相对应，基于Systolic结构的并行运算结构更适合于这种数据更新的运算，仅需要将新采集的数据按顺序送入Systolic阵列中即可。

4.1 Systolic并行处理阵列

Systolic并行处理器是一种流水线型的阵列结构，它是1978年H.T.Kung等在以大规模并行处理为目的而研究专用VLSI结构时提出的［10］。Systolic系统是一个节律性的完成数据计算并通过系统传递数据的处理器网络。其结构具有模块化、规则化、局部连接、高度流水以及高同步化多重处理等重要特性。

图1 Systolic阵列的基本原理

图1 给出了Systolic阵列的基本原理。Systolic阵列中，数据一旦从存储器中取出后，就沿着阵列从一个PE“泵”到另一个PE，而在它通过的每个PE上，数据都可以被有效的利用。这样，在从存储器调出的数据又返回存储器之前，使之通过尽可能多的PE，进行流水线式的处理，减轻了主机的输入输出负担。Systolic阵列具有高效率的原因在于主机端负责数据的存储，且主机端还可以选择所需的数据，并将数据流水式的送入阵列。

4.2 逆OR分解SM I算法的Systolic实现

综合上面的论证和分析，可以得到LCMV准则下避免前向后向带入的逆QR分解SMI算法的实现步骤：

2）递推更新（k=1，2，…）：计算中间向量z(n)，并根据式（17）计算得到旋转所用的酉阵P(n)，并用P(n )通过式（16）和式（20）更新下三角阵A-nH和中间向量vn。

根据上述逆QR分解SMI算法的内在数据处理并行性，我们能得到该算法的Systolic阵列实现结构。图2给出以四阵元为例的逆QR分解SMI算法的Systolic并行实现结构。

图2 逆QR分解SMI算法的Systolic结构

从图中可以看出，通过算法的改进该Systolic阵列避免了传统QR分解SMI算法的前向后向带入过程，使得实现过程变得简洁。从图中可以看出，该Systolic阵列共包含四种PE单元，它们分别表示：中间向量v，各vi单元完成对vi的存储和更新；中间向量z(n)，各单元zi单元用来产生系统进行Givens旋转更新所需的旋转因子；下三角矩阵B=A-nH的下三角部分bij单元存储并更新A-nH的各元素；wi单元完成权向量的更新和输出。图3给出了各功能单元的具体实现方法。

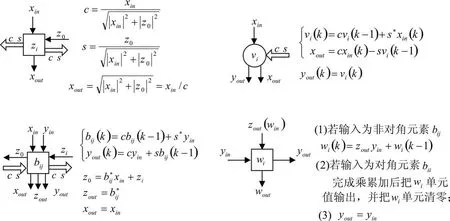
图3 各PE单元的功能实现

5 STMV算法的FPGA并行实现方法

图4给出了STMV波束形成算法的硬件实现原理图，并给出了逆QR分解SMI自适应波束权矢量提取算法在FPGA上实现的原理结构。

在该实现结构中，每路阵元的接收信号均连有一个FIFO（先入先出）存储器，该存储器用以完成A／D采集信号的接收、存储和读取。存入各路FIFO的数据通过写使能（REN）的控制接入Systolic阵列权提取模块，进行接收信号的自适应权矢量提取。要想完成整个波束形成的设计，还应在Systol⁃ic阵列权提取模块后加入波束形成模块，或是将该FPGA的全矢量输出和采集数据接入DSP处理器由DSP完成波束形成部分的运算。

图4 逆QR分解SMI算法在FPGA上的实现结构

图4 中的FIFO存储器是通过调用XILINX公司的IP核生成软件Core Generator生成的，所使用的IP核为Asynchronous FIFO v6.1。该异步FIFO可以对写入和读出端分别进行时序控制。数据输入端的数据总线（DIN）可直接与A/D端的数据总线相连接，配合写使能（WEN）和写时钟（WCLK）可以完成采集信号到FIFO存储器的存入。同时该FIFO的输出端还配有全满（FULL）、几乎满（ALMOST FULL）和全空（EMPTY）、几乎空（ALMOSTEMPTY）信号，用以方便对其进行时序控制，其中满和几乎满信号是与写时钟（WCLK）同步的，空和几乎空信号是与读时钟（RCLK）同步的。为了更进一步对FIFO进行时序控制，该IP核还提供写计数（WR COUNT）与读计数（RD COUNT）输出信号，用以标识该FIFO读写状态。配合算法的输入时序，各路FIFO的输出信号可通过读使能（REN）信号的控制进行输出。数据输出总线（DOUT）直接连入Systol⁃ic阵列的各路输入，经过该Systolic阵列即可完成自适应权矢量的提取和输出。

6 结语

本文从STMV波束形成算法的并行实现角度入手，在讨论了STMV波束形成算法原理的基础上，提出了STMV波束形成算法的逆QR分解SMI的实现方法，讨论了逆QR分解SMI算法的Systolic阵列并行实现结构，分析组成Systolic阵列的各PE单元的基本运算模块的实现，并研究了逆QR分解SMI算法基于Systolic阵列结构的FPGA并行实现方法和STMV波束形成算法并行实现的硬件构架。

［1］李启虎.声纳信号处理引论（第二版）［M］.北京：北京海洋出版社，2003：12-15.

LIQihu.Sonar signal processing Introduction（Second Edi⁃tion）［M］.Beijing：Beijing Ocean Press，2003：12-15.

［2］VAN TREE L.Optimum array processing［M］.New York：John Wiley&Sons Inc.，2003：48.

［3］CAPON J.High resolution frequency-wave number spec⁃trum analysis［J］.Proceeding of the IEEE，1969，57（8）：1404-1418.

［4］KROLIK J，SWINGLERD.Multiple broadband source lo⁃cation using steered covariance matrices［J］.IEEE Trans Acoustics Speech and Signal Processing，1989，37（10）：1481-1494.

［5］贡三元.VLSI阵列处理［M］.南京：东南大学出版社，1990：56-80.

GONG Sanyuan.VLSI array processing［M］.Nanjing：Southeast University Press，1990：56-80.

［6］J.Krolik.D.Swingler.Multiple Broadband Source Loca⁃tion Using Steered Covariance Matrices.IEEE Trans.AS⁃SP.1989，37（10）：1481-1494.

［7］冯地耕.基于QR分解的ADBF算法及其DSP实现研究［D］.西安：西安电子科技大学，2004：35-43.FENG Digeng.ADBF algorithm based on QR decomposi⁃tion and its DSPRealization［D］.Xi’an：Xi’an University of Electronic Science and Technology，2004：35-43.

［8］石斌斌，钱林杰.基于CORDIC的滑窗最小二乘递推算法［J］.系统工程与电子技术，2010，32（11）：2304-2309.

SHI Binbin，QIAN Linjie.CORDIC-based sliding window recursive least squares algorithm［J］.Systems Engineering and Electronics，2010，32（11）：2304-2309.

［9］白振锋，萧宝瑾.智能天线自适应波束形成算法的研究［J］.山西电子技术，2007（1）：54-57.

BAIZhenfeng，XIAO Baojin.Study of Smart antenna adap⁃tive beam-forming algorithm［J］.Shanxi Electronic Tech⁃nology，2007（1）：54-57.

［10］孙世新，卢光辉.并行算法及其应用［M］.北京：机械工业出版社，2004：33-45.

SUN Shixin，LU Guanghui.Parallel algorithm and its ap⁃plication［M］.Beijing：Mechanical Industry Press，2004：33-45.

Research of STMV Beam-form ing A lgorithm Parallel Processing Im p lementation M ethod

ZHOU Yijun LIU Qianli
（Military Representative Office of Navy in Wuhan 438 Factory，Wuhan 430060）

TP23

10.3969/j.issn.1672-9722.2017.09.009

2017年4月17日，

2017年5月27日

周亦军，男，高级工程师，研究方向：水声工程。刘千里，男，博士研究生，工程师，研究方向：水声工程。