基于偏好排序淘汰NSGAII算法的短波网络多区域重点覆盖优化方法

2017-10-14李新超贺前华李艳雄朱铮宇

电子与信息学报 2017年8期

李新超贺前华李艳雄朱铮宇

李新超贺前华*李艳雄朱铮宇

(华南理工大学电子与信息学院广州 510640)

在采用偏好NSGAII算法求解多子区域重点覆盖的短波网络频率优化指配时，针对算法中非支配排序耗时较多的问题，该文提出一种偏好排序淘汰的NSGAII算法。在进行非支配排序前，根据解的偏好评价排序结果淘汰一部分偏好评价较差的解，减少参与非支配排序的解的数量从而减少求解时间，同时降低偏好评价结果较差的个体解被选中进行交叉、变异的概率，提高算法的求解效率和求解效果。在进行的48组数据测试中，该文算法在其中38组决策解偏好评价结果和求解时间同时最优，相同迭代次数时相比偏好NSGAII算法节省27%的求解时间。结果表明通过偏好排序淘汰机制的引入，更好利用了偏好信息，使算法用较少的时间求得更好的偏好解。

短波网络；频率指配；多目标优化；非支配排序；偏好排序淘汰

1 引言

短波通信具有通信距离远、抗毁能力强、建设成本低等优点[1]，在军事通信、应急救灾、海洋渔业等领域有着不可替代的作用[2]。短波通信频率是影响其通信质量的关键因素之一[3]，但频率资源日趋紧张。因此针对大区域应急短波网络，岸海短波网络等不对等短波网络进行频率优化指配具有重要意义[4]。不对等短波网络常态下的频率优化已有文献进行了研究[5]，但应急短波网络、岸海短波网络等除在常态下满足区域内机动电台的随遇接入需求外，在一个或多个区域发生突发事件时，还需要提高网络对事发区域的可覆盖台站个数从而为区域内的多个应急机动电台提供更可靠的通信保障[6]。因此根据事发区域的保障需求，在每个电离层变化相对稳定的时段内，快速找到可对子区域进行重点覆盖，且尽可能保障全网覆盖最优的频率指配方案则非常重要。目前针对该问题的研究文献较少，问题可抽象为一个多目标组合优化问题。

针对多目标优化问题，采用Pareto最优求解的相关算法求出一组Pareto最优解，由决策者进行选择是目前的主流方法[7]，但相关算法求得的Pareto解数目较多，决策者较难选择，且有许多决策者基本不会考虑的解，对这些解的搜索降低了算法效率。因此将决策者的偏好需求加入到Pareto求解过程的偏好多目标算法成为研究热点[8]，按照偏好信息的不同主要有：参考点，参考方向[8]等简单的偏好信息，其求解效果一般但对解的Pareto分布的普适性较好；角度偏好、雷达搜索[9]、光束搜索[10]等结合Pareto解分布情况增加了约束的偏好信息，在一些情况下更为有效，但参数设置复杂；g-dominance[11], r-dominance[12]等通过偏好信息改变Pareto解的支配关系的偏好算法，实验表明该类偏好算法在通常情况下更为有效[12]，但对于一些近似水平或垂直分布的Pareto前端，容易造成解的丢失，影响求解性能[13]。各种偏好算法各有优缺点，需要结合问题特点进行选取[10]。

本文的多子区域重点覆盖的频率优化问题，子区域的覆盖情况通常未知，但覆盖要求和覆盖任务的重要程度通常可知且可能不同，可以将子区域覆盖任务重要程度作为偏好参考方向或子区域的覆盖要求作为偏好参考点。在目标重要程度不同时采用目标权重参考方向则更为合适[14]。文献[14]将偏好参考方向和由遗传算法(Genetic Algorithms, GA)发展而来的性能优异的多目标优化算法NSGAII (Non-dominated Sorting Genetic Algorithms II, NSGAII)算法[9]结合，以种子解在偏好参考方向上的权重和作为评价种子解优劣的指标，增强Pareto求解沿偏好参考方向的搜索以求得决策者需求的解，因此本文利用子区域覆盖任务的重要程度作为偏好参考方向并结合NSGAII算法对多子区域重点覆盖的频率优化问题进行求解。

在NSGAII等算法中，采用非支配排序的拥挤距离计算机制可以使Pareto精英解得到保留并分布均匀合理[14]，但该过程也是算法中最耗时的环节之一[15]，影响算法的效率。围绕非支配排序产生了一些改进算法，提高了效率[16]，但提高的幅度也很有限。

本文结合短波网络多子区域重点覆盖的频率优化问题的特点和需求，在采用参考方向的偏好NSGAII算法求解时，针对算法中非支配排序过程耗时及偏好信息利用不足的问题，在算法进行非支配排序前，根据解的偏好评价进行排序，先淘汰一部分决策者不会考虑的偏好评价较差的解，减少参与偏好排序的解的数量，同时减少偏好评价差的解被选中遗传的概率，提高算法的求解效果和效率。

2 短波网络多区域多重保障问题的数学模型

2.1 决策变量及约束条件

本文研究的不对等短波网络由一个短波核心网络和若干机动电台构成，核心网络台站通过有线互通，短波通信在短波核心网络台站和机动电台之间进行，频率优化指配针对核心网络台站实现[5]。短波台站的有效通信区域形状通常不规则，需要将目标区域划分为小的单元格以实现计算[6]。将目标区域划分为个格，整个区域用矩阵表示。重点通信覆盖的子区域表示为,为子区域编号，共个。如果单元格属于子区域，则，否则为0,,对应单元格的坐标，,。全网覆盖可作为一个为全1的子区域。

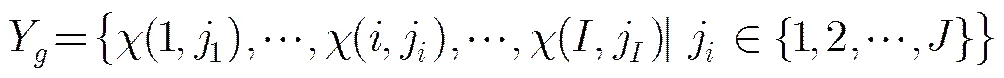
由于短波传输距离较远，为避免同频干扰，一个方案中一个频率点只能使用一次。若属于，则，否则。该约束条件表示为

(2)

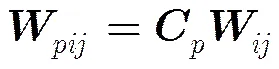
2.2目标函数

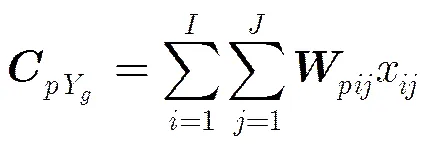
(5)

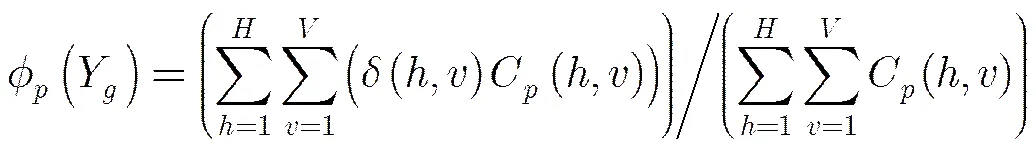
(7)

2.3目标函数的Pareto解定义

由于网络台站频率资源的限制，多个子区域很难同时达到最优覆盖保障，可能不存在最优解，因此需要采用Pareto最优相关概念描述解的关系。

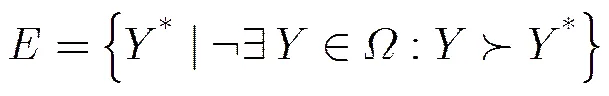
(9)

2.4 Pareto解的偏好评价

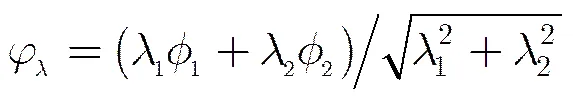
3 偏好排序淘汰的偏好NSGAII算法

3.1偏好排序种群淘汰机制的引入

3.1.1算法的思路在 NSGAII等算法中，非支配排序时间复杂度由参与排序解的个数和目标数确定，是算法中耗时最多的步骤之一[15]。文献[16]的研究表明，一些非支配排序改进算法在特殊情况下可使该过程的时间复杂度降为，但通常情况下的复杂度为，仍需要大量的时间。

在偏好NSGAII算法中，仅利用偏好评价作为种子解被选中进行交叉、变异的概率，存在偏好信息利用不足的问题。在迭代解及外部档案解合并后非支配排序前，更好地利用偏好评价信息，将偏好评价较差的一部分解先淘汰掉，减少参与非支配排序的解的数量可以减少求解时间，且减少了偏好评价较差的种群解被选中的概率，从而提高算法的求解效果和效率。

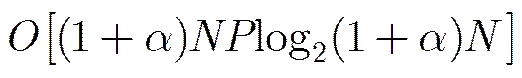
(12)

式(12)的时间复杂度小于式(11)时，本文算法即可减少求解时间，在,已知时，求得，当,,时，即的情况下，，当接近取值范围中值时既可以均衡发挥非支配排序和偏好排序淘汰的作用，此时该步骤相比偏好NSGAII算法节省33%的时间。当，其他条件相同时，，当时节省41%的时间。

3.2算法的框架

本文的偏好排序淘汰NSGAII(preference ranking elimination NSGAII, pre-NSGAII)算法求解短波网络多子区域重点覆盖的频率优化指配时，用频方案的染色体采用整数编码，用频方案对子区域的覆盖率为对应个体解的适应度值。采用式(10)计算个体解的偏好评价值，算法框架如图1。

4 实验仿真及分析

4.1实验条件及评价指标

选取以28ºN, 104ºE为中心的边长为6×103km的方形区域作为短波网络的区域场景，区域划分为边长20 km的9×104个方格以实现算法的仿真评估。短波核心网络由36个125 W的固定台站构成，可用频率点数为77[5]。时间背景选取2015年1月。

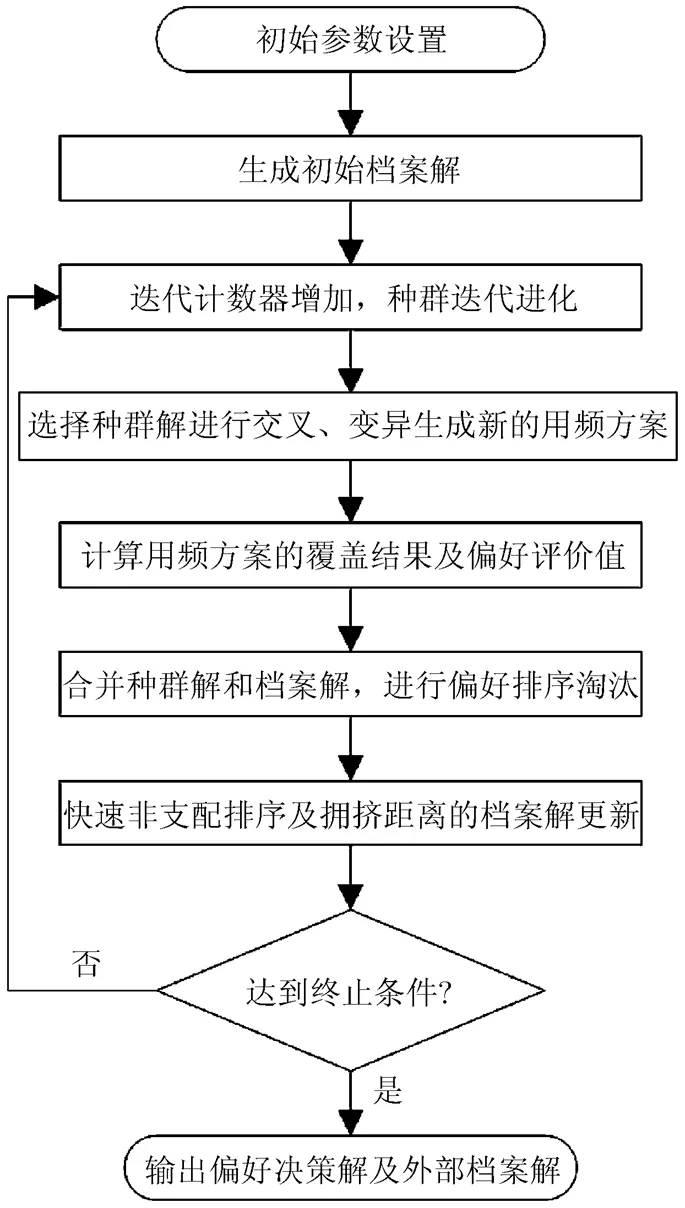
图1 pre-NSGAII求解多目标频率指配的算法框架

采用本文的pre-NSGAII算法，目标偏好加权的单目标p-GA算法、NSGAII算法、目标偏好加权的p-NSGAII[14], g-NSGAII[15]，针对以上两种情形以1 h为时段进行24 h的覆盖优化求解。

从各组算法求得的最优决策解的偏好评价值、Pareto前沿解的分布情况、求解时间3个方面对各组算法进行评价。对NSGAII算法从最终Pareto集中按照式(10)挑选一个偏好评价最优解作为决策解。对于本文的问题，每个时段真正的Pareto前沿解的分布是未知的，因此将描述两个Pareto集的测度[18]进行扩展，通过多个Pareto集在最终的Pareto前沿解集的占优比例进行Pareto解集分布广度评价，其子集占优越多测度越大，说明算法求得的Pareto前端分布广度越好。

4.2实验及结果分析

4.2.1两个目标的实验结果两个目标24个时段的覆盖优化结果分为两类情况，在短波通信条件较差的时段如2~6点，13~15点，所有算法求得的解均未达到期望覆盖。在通信条件较好的时段如1点，7~12点，18~24点，部分算法求解达到期望覆盖而提前终止，其Pareto前端是一个解。

表1 5组算法两个目标3个指标的最优次数统计

图3(a)中4时段的Pareto分布表明，在覆盖较差的时段，单目标p-GA算法求解效果不如多目标相关算法，NSGAII算法Pareto前端的分布域较广，但对偏好解的求解不如3种偏好多目标算法。3种偏好算法中，本文的pre-NSGAII算法，通过偏好淘汰，利用了更多的偏好信息，效果最好。结合表2的最优决策解评价值及求解时间可以看出，本文算法求解效果和时间均优于其他算法，在同样迭代次数下，相比p-NSGAII算法节约了27%的时间。

在覆盖较好的10时段，除p-GA外所有算法都达到了期望覆盖，从图3(b)难以区分算法性能，但结合表2的求解时间可以看出本文算法求解时间最短，效率最高。图3 为两个时段的最优决策解的覆盖效果，从图4(a)与图4(b)可以看出，的时段实现了全网区域2个覆盖，子区域覆盖效果也优于时段。

4.2.2 3个目标的实验结果 3个目标情形下的实验类似两个目标，由于通信条件、资源的限制，子区域重点覆盖任务要求的增加，与两个目标相比，24个时段中，未达到期望覆盖的时段增加为15个，为1~8点，11~17点时段。达到覆盖期望而提前终止的时段减少为9个，为9~10点，18~24点时段。根据上述情况两类(未达到覆盖期望的15个时段)、(达到覆盖期望的9个时段) 各组算法,,的统计如表3所示。

图4两个目标较差、较优时段的最优覆盖

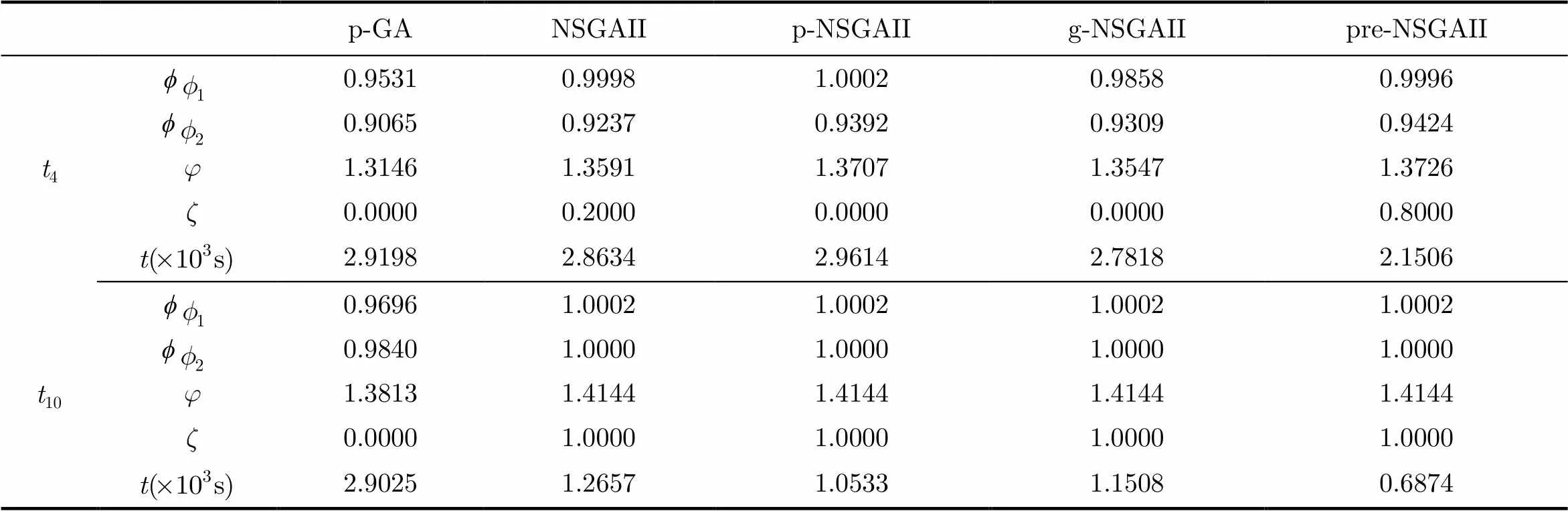
表2 5组算法两个目标较差、较优时段的求解情况

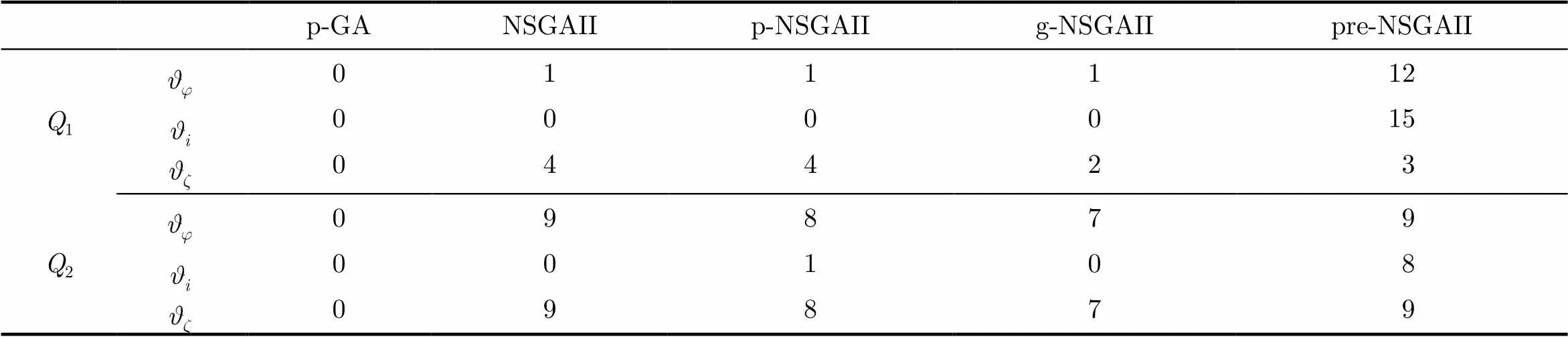
表3 5组算法3个目标问题3个指标的胜出次数统计

从表3的统计可以看出，算法性能的比较结果与两个目标情况基本一致，在类的15个时段中，本文算法的,分别为12和15。在类的9个时段中，本文算法的为8，均优于其他算法。

综合两个目标和3个目标各24个时段共48组测试数据的求解情况，本文算法在38组上偏好评价值和求解时间均最优，表明本文的pre-NSGAII算法通过偏好排序淘汰机制提高了算法偏好求解的效果和效率。

4.2.3淘汰剩余率取值实验分析偏好淘汰率是影响偏好排序淘汰和非支配排序机制的发挥作用的关键参数之一，为此选取上述的和时段，分别取1.00, 1.25, 1.50, 1.75, 2.00, 2.25, 2.50(仅3个目标)进行偏好淘汰率取值实验，并与p-NSGAII进行比较，各取值分别运行5次所求得的最优覆盖的偏好评价值及求解时间平均如图7所示。

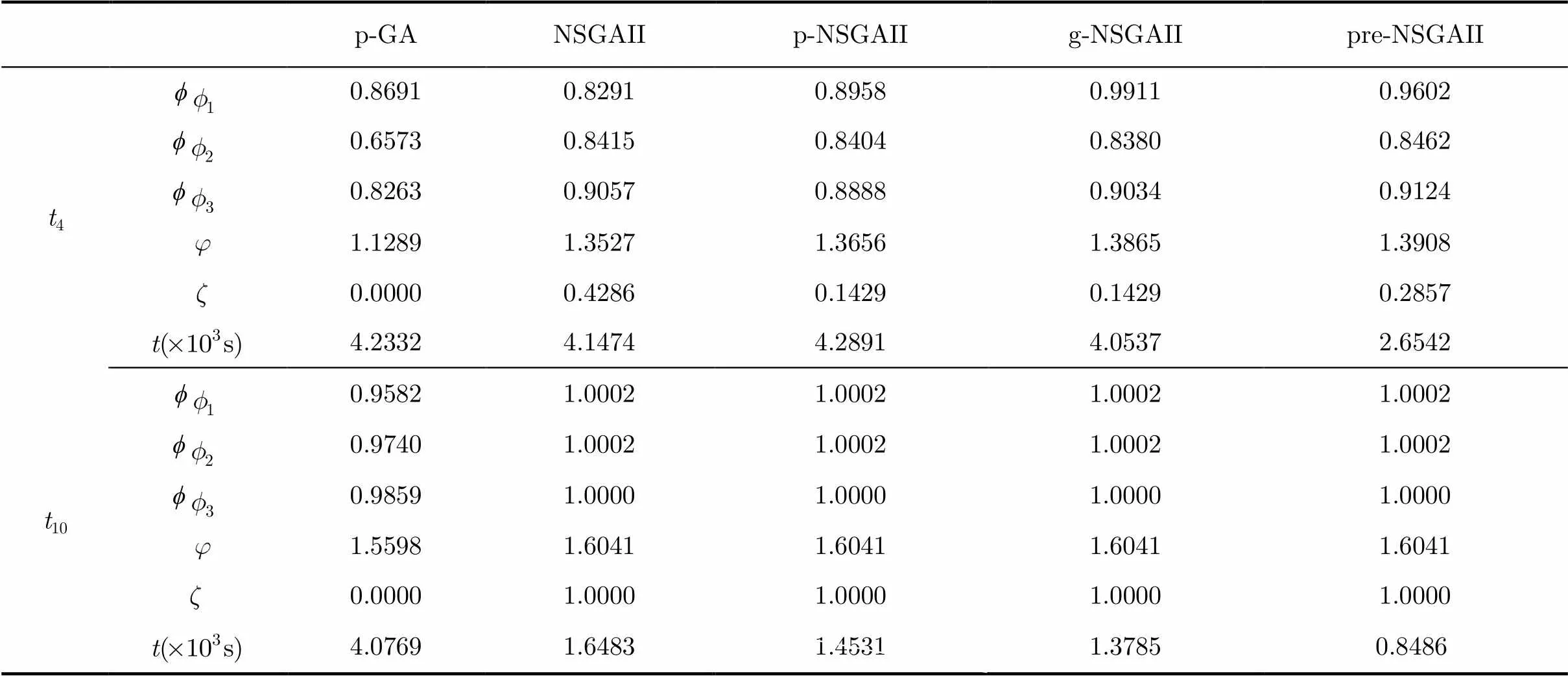
表4 5组算法3个优化目标时较差、较优时段的求解情况

图5 5组算法求得的3个目标较差、较优时段的Pareto解分布

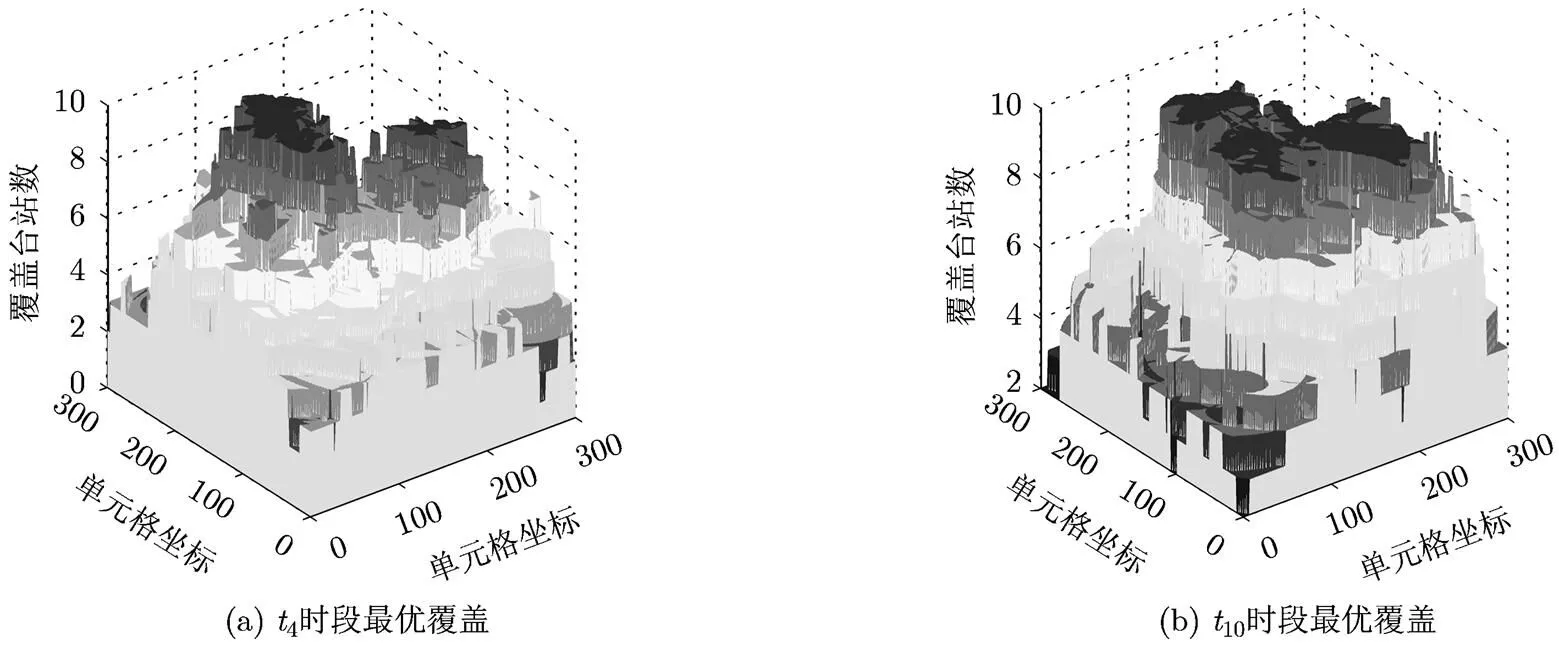
图6 3个目标两个子区域较差、较优时段的最优覆盖

5 结束语

对子区域重点覆盖保障的短波网络频率优化指配这一多目标优化问题，在采用偏好NSGAII算法求解时，针对算法求解中的非支配排序这一步骤耗时较多的问题，提出了偏好排序淘汰的偏好NSGAII算法。该算法在种群解和外部档案解合并后进行非支配排序前根据偏好评价信息进行排序淘汰，淘汰一部分偏好评价较差的解，减少参与非支配排序的解的数量，同时减少后续对偏好评价差的解区域的搜索。在两个目标和3个目标共48组测试数据中，本文算法相比p-GA, NSGAII, p-NSGAII, g-NSGAII算法在38组上的决策解偏好评价结果和求解时间同时最优，表明通过偏好排序淘汰机制的引入，本文算法可以在节省求解时间的同时取得较好的求解效果。但在Pareto前沿解集的分布广度上，本文算法表现一般，说明算法在偏好方向上穿透能力增强的同时，解集的分布广度受到了影响。将该偏好排序淘汰机制引入其他采用非支配排序的偏好多目标算法是下一步研究的方向。

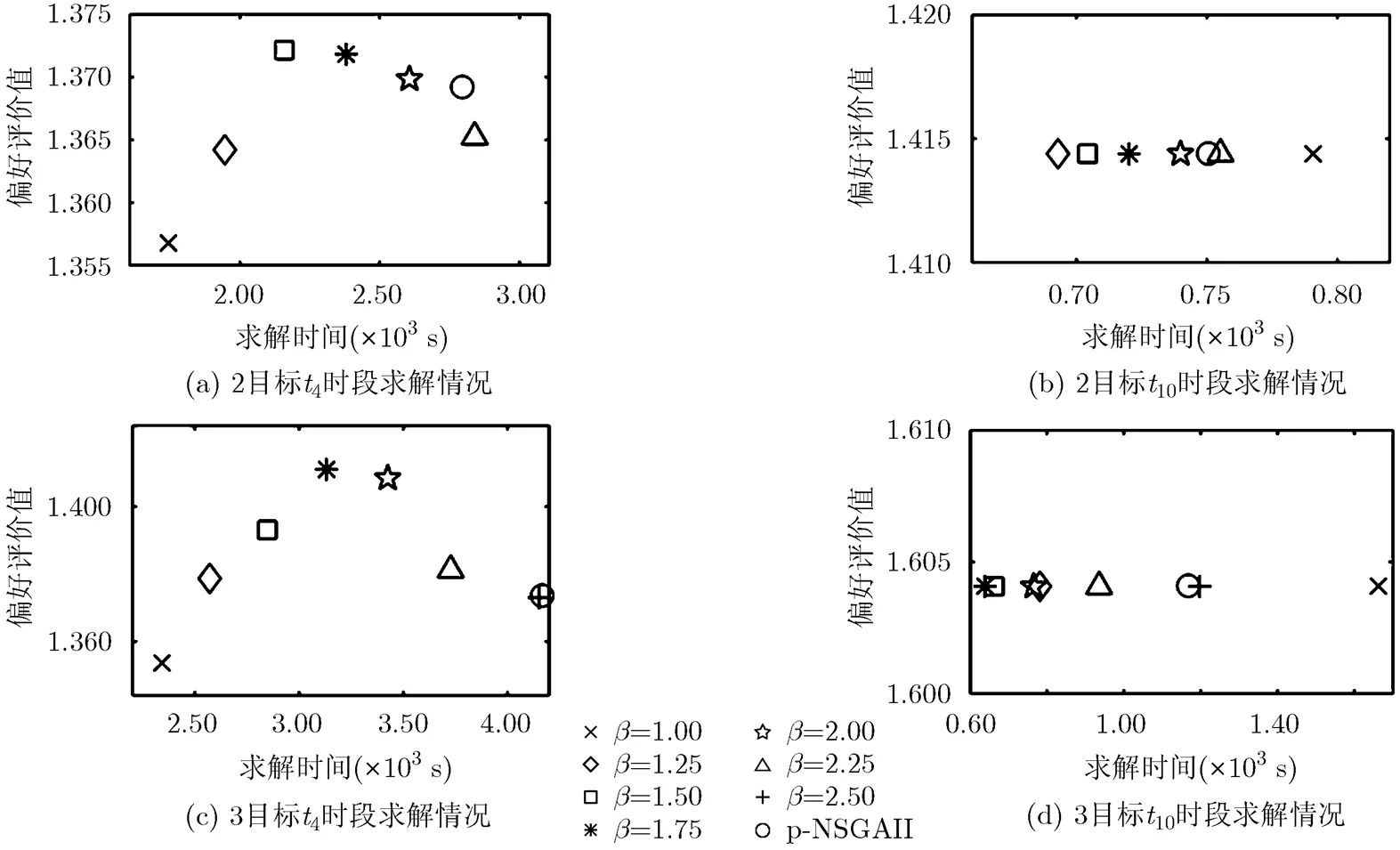
图7 淘汰剩余率取值实验情况

[1] 王俊江, 柳文, 焦培南. 基于返回散射探测和干扰监测的短波通信实时选频系统[J]. 电子学报, 2012, 40(4): 729-733. doi: 10.3969/j.issn.0372-2112.2012.04.017.

WANG Junjiang, LIU Wen, and JIAO Peinan. Real-time frequency selection system in HF communication based on backscatter sounding and interference monitoring[J]., 2012, 40(4): 729-733. doi: 10.3969/j.issn. 0372-2112.2012.04.017.

[2] BAYNAT B, PROUVEZ R, KHALIFE H,. Modélisation d’un mécanisme de prise de ligne dans les réseaux de communication HF[J]., 2015, 28(8): 42-46.

[3] 景渊, 李栓红, 杨峰, 等. 短波IP网络中速率自适应与SR- ARQ性能分析[J]. 系统工程与电子技术, 2013, 35(1): 184-190. doi: 10.3969/j.issn.1001-506X.2013.01.31.

JING Yuan , LI Shuanhong, YANG Feng,. Performance analysis of rate adaptation and SR-ARQ in high frequency IP network[J].&, 2013, 35(1): 184-190. doi: 10.3969/j.issn.1001-506X.2013.01.31.

[4] 朱振飞, 刘毅敏, 吴永宏, 等. 短波网动态频率管理系统的状态查询设计[J]. 电波科学学报, 2013, 28(3): 65-69. doi: 10.13443/j.cjors.2013.03.016.

ZHU Zhenfei, LIU Yimin, WU Yonghong,. A method of link status inquiry for HF network dynamic frequency management[J]., 2013, 28(3): 65-69. doi: 10.13443/j.cjors.2013.03.016.

[5] 李新超, 贺前华, 李艳雄, 等. 基于互信息扩散蚁群算法的短波频率优化指配[J]. 华中科技大学学报(自然科学版), 2016, 44(4): 6-11. doi: 10.13245/j.hust.160402.

LI Xinchao, HE Qianhua, LI Yanxiong,. HF frequency assignment based on ant colony algorithm utilizing mutual information pheromone diffusion[J].(), 2016, 44(4): 6-11. doi: 10.13245/j.hust.160402.

[6] 杨青彬, 余毅敏, 郭马坤, 等. 大区域网络化应急短波通信中的频率管理方法[J]. 电讯技术, 2013(4): 470-475. doi: 10 .3969/j.issn.1001-893x.2013.04.019.

YANG Qingbin, YU Yimin, GUO Makun,. Frequency management methods for large regional network of emergency HF communication[J]., 2013(4): 470-475. doi: 10.3969/j.issn.1001-893x. 2013.04.019.

[7] 公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2): 271-289. doi: 10.3724/SP.J.1001. 2009.03483.

GONG Maoguo, JIAO Licheng, YANG Dongdong,. Research on evolutionary multi-objective optimization algorithms[J]., 2009, 20(2): 271-289. doi: 10.3724/SP.J.1001.2009.03483.

[8] KHARE V, YAO X, and DEB K. Performance Scaling of Multi-objective Evolutionary Algorithms[M]. Evolutionary Multi-Criterion Optimization, Springer Berlin Heidelberg, 2015: 376-390.

[9] HU Jianjie, YU Guo, ZHENG Jinhua,. A preference-based multi-objective evolutionary algorithm using preference selection radius[J]., 2016: 1-27. doi: 10.1007/s00500-016-2099-9.

[10] 巩敦卫, 王更星, 孙晓燕. 高维多目标优化问题融入决策者偏好的集合进化优化方法[J]. 电子学报, 2014, 42(5): 933-939. doi: 10.3969/j.issn.0372-2112.2014.05.015.

GONG Dunwei, WANG Gengxing, and SUN Xiaoyan. Set-based evolutionary optimization algorithms integrating decision-maker's preferences for many-objective optimization problems[J]., 2014, 42(5): 933-939. doi: 10.3969 /j.issn.0372-2112.2014.05.015.

[11] MOLINA J, SANTANA L V, HERNANDEZ-DIAZ A G,. g-dominance: Reference point based dominance for multiobjective metaheuristics[J]., 2009, 197(2): 685-692. doi: 10.1016/j.ejor.2008.07.015.

[12] LIU Ruochen, SONG Xiaolin, FANG Lingfen,. An r-dominance-based preference multi-objective optimization for many-objective optimization[J]., 2016: 1-22. doi: 10.1007/s00500-016-2098-x.

[13] WANG S, ALI S, YUE T,. UPMOA: An improved search algorithm to support user-preference multi-objective optimization[C]. IEEE 26th International Symposium on Software Reliability Engineering, Gaithersbury, MD, USA, 2015: 393-404. doi: 10.1109/ISSRE.2015.7381833.

[14] DEB Kalyanmoy, and KUMAR Abhishek. Interactive evolutionary multi-objective optimization and decision- making using reference direction method[C]. Genetic and Evolutionary Computation Conference, GECCO 2007, Proceedings, London, 2007: 788-802. doi: 10.1145/1276958. 1277116.

[15] 曾三友, 李晖, 丁立新, 等. 基于排序的非劣集合快速求解算法[J]. 计算机研究与发展, 2004, 41(9): 1565-1571.

ZENG Sangou LI Hui, DING Lixin,. A fast algorithm for finding non-dominated set based on sorting[J]., 2004, 41(9): 1565-1571.

[16] ZHANG X, TIAN Y, CHENG R,. An efficient approach to non-dominated sorting for evolutionary multi-objective optimization[J]., 2015, 19(2): 201-213. doi: 10.1109/TEVC. 2014.2308305.

[17] YAN Z, ZHANG L, RAHMAN T,. Prediction of the HF ionospheric channel stability based on the modified ITS model[J]., 2013, 61(6): 3321-3333. doi: 10.1109/TAP.2013.2249571.

[18] ZITZLER E and THIELE L. Multi-objective evolutionary algorithms: A comparative case study and the strength pareto approach[J]., 1999, 3(4): 257-271. doi: 10.1109/4235.797969.

Multi-areas Outstanding Covering Optimization Method of HF NetworkBased on Preference Ranking Elimination NSGAII Algorithm

LI Xinchao HE Qianhua LI Yanxiong ZHU Zhengyu

(,,510640,)

This paper proposes a preference ranking elimination NSGAII algorithm to deal with the time-consuming issue of the preference NSGAII algorithm in optimizing HF network frequency assignment in multi-areas outstanding coverage. The proposed algorithm sorts and eliminates solutions according to their preference evaluation priori to the non-dominate sorting. By eliminating solutions with low ranking, the number of solutions participates in non-dominate sorting is reduced. The calculation time and the probability of selecting low ranking individuals for crossover or mutation are both decreased. The proposed algorithm simultaneously achieves the best performance and least calculation time in 38 of 48 sets experiments. Constrained with the same iteration number, the proposed algorithm saves 27% of computation time against the preference NSGAII algorithm. Experimental results show that by adopting preference evaluation sorting, the proposed algorithm takes less time and obtains a better solution.

High Frequency (HF) network; Frequency assignment; Multi-objective optimization; Non-dominate sorting; Preference ranking elimination

TN92

1009-5896(2017)08-1779-09

10.11999/JEIT161172

2016-11-02；

改回日期：2017-03-01；

2017-04-25

贺前华 eeqhhe@scut.edu.cn

国家自然科学基金(61571192)，广东省公益研究(2015A 010103003)

The National Natural Science Foundation of China (61571192), The Public Welfare Research Project of Guangdong Province (2015A010103003)

李新超：男，1980年生，博士生，研究方向为短波通信及智能优化.

贺前华：男，1965年生，教授，主要研究方向为音视频信号处理.