浅海环境不确定性对声场扰动的影响

高飞，潘长明，孙磊，桂发银



浅海环境不确定性对声场扰动的影响

高飞，潘长明，孙磊，桂发银

(海军海洋测绘研究所，天津300061)

探索海洋环境各水声参数的不确定性所引发的声场扰动，对提高水声场预报的准确性与科学性至关重要，极具理论意义与应用价值。基于Workshop’97浅海环境基准模型，以扰动声场与实际声场的相关性函数作为量化指标，通过Kraken波动理论数值模型与马尔科夫链蒙特卡罗随机统计思想，基于单因子变量原则模拟分析了浅海水平不变环境中各水声参数声场扰动敏感性大小及其相关性，结果表明：沉积层声速1、水深1敏感性最强，沉积层衰减系数α沉积层密度ρ沉积层声速2沉积层厚度2基底声速3次之，基底衰减系数α基底密度ρ几乎无影响；α、ρ、1、1敏感性随距离增加逐渐增强，223敏感性随距离增加逐渐减弱；2、2，2、3，1、3，2、3之间存在较强的正相关性，2、1，1、2之间为显著的负相关性。

海洋环境不确定性；声场扰动；相关性；似然函数；Kraken简正波模型；马尔科夫链蒙特卡罗方法

0 引言

基于确定频率、功率、指向性的声源预报其水声场的分布特征，对水下声源定位[1-2]、地声参数反演[3-4]、声呐有效探测距离评估[5-6]等具有重要的参考意义和应用价值。

海洋环境对水声场影响显著已被大量研究所证实[7-9]，然而海洋环境的时空多变性、不确定性成为准确有效预报水声场的重要制约因素之一，故研究各海洋环境要素不确定性导致的水声场扰动尺度大小显得尤为重要。Donald[10]等人分析了水深失配对匹配场声源定位的影响，指出在100 m浅水海域，当水深波动±3.5 m，且计算水深大于实际水深时，声源定位结果比实际偏近、偏深。Shang[11]等人基于波动理论模型，分析水深、海底沉积物类型、声速剖面对各模态简正波水声场的影响。Kevin[12]等人通过计算声压幅度概率密度函数，用以评估水声场在不同的不确定海洋环境参数条件下的敏感性。赵航芳[13]等人利用NRL(Navy Research Library)Workshop’93典型浅海环境，分析各水声环境参量不确定性对Bayes匹配场性能的影响，较好地量化了参数失配的灵敏度。王文博[14]等人讨论了水平不变波导中声速剖面的扰动及海面、海底起伏等条件下的声强概率分布模型，并利用蒙特卡罗(Monte Carlo)方法进行了声场敏感性分析。

然而，已有的研究工作只是针对部分参数，研究其对声场扰动能量的影响，没有考虑不同参数对声场扰动敏感性随距离的变化，也未提及参数间的相关性。本文基于Workshop’97浅海环境基准模型，讨论了150 Hz声信号在水平不变海洋环境中的传播特征，借鉴Bartlett匹配场处理器构建扰动声场与实际声场的相关性函数，并利用马尔科夫链蒙特卡罗(Markov Chain Monte，MCMC)统计方法与波动理论水声数值模型模拟各海洋环境参数变化时，各环境参数对声场扰动的影响及其之间的相关性。

1 基本原理

1.1 波动理论模型

依据Helmholtz方程解算方法的差异，常见的水声传播建模理论可分为：简正波法、抛物方程法、射线法、波数积分法和有限元法。简正波法对计算水平不变的声场效率较高，可较好地解决边界处理问题，在研究海洋环境变化对水声场的影响中应用广泛。

Kraken模型[15]是一种常见的水平不变简正波理论模型(模型代码下载地址：http://oalib.saic.com)，基于Helmholtz方程变量分离，在柱坐标系中，与时间无关的单频声压函数表示为一系列简正波的叠加：

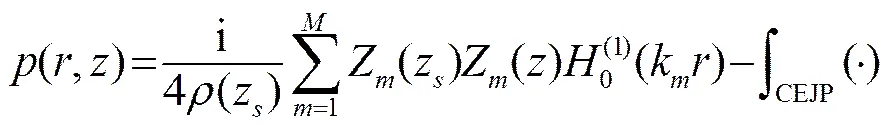
1.2 浅海声传播环境模型

浅海环境对声传播的影响因素大致可分为上、下边界及海水声速剖面，由于空气声阻抗远小于海水，声波在上边界的反射系数≈1，故其所造成的能量损失可近似忽略。

海水影响造成声扰动的主要因素有声速剖面、水深。浅海夏秋季节声速大小随水深的变化通常具有强跃层现象，冬春季节该现象消失。声速剖面主要用于研究海洋中尺度现象(跃层、中尺度涡、内波、海洋峰等)对声场扰动的影响，其作用表现为对能量沿深度分布的控制能力，对“碰撞”界面次数及“碰撞”角度的控制，以及对能量传播速度(群速度)的控制。然而，较海底密度、声速等参数，海水声速剖面变化显著，且赵航芳[13]等人的研究工作中指出了海水声速梯度对Bayes匹配场性能的影响显著，故下文不再针对水中声速剖面的作用进行分析。

当前，两层水平不变海底参数模型应用较为广泛，可分为沉积层、基底层，其声速、密度、衰减系数是声场数值计算的重要参量。沉积层覆盖于基底之上，通常考虑其声速的垂向变化，忽略基底层声速的空间变化。

Tolstoy[16]等人基于实测水声调查数据，提出了Workshop’97浅海环境基准模型(见图1)，该模型是Workshop’93[17]的改进，最初的设计用于地声参数反演，后常被学者用于水声定位及不确实海洋环境分析。

图1中所示的浅海环境基准模型中含9个参量，水深为1，沉积层厚度为2，声速由1线性变化至2，基底声速为3，设沉积层、基底衰减系数()与密度(、)为常数。

实际声场预报中，需构建确定的海洋环境背景场参数，用以融入数值模型进行计算。然而，受海洋环境时空多变性的影响，1通常无法准确获取，而且受当前海底环境测量技术的限制，地声参数难以预知。故文章以Workshop’97浅海环境基准模型进行分析，相关参数的物理含义、单位、实际值与不确定变化区间如表1所示。

设置各参数变化区间应以其实际值及其常见取值分布为依据，参考文献[2,10,11,13]中参数的不确定性变化区间，对各参数变化区间进行设置。其中，1为水深值，该参数的测量手段相对成熟，其近海精度主要受潮汐、海底地形的影响，故设置相对较小的变化区间[95,105]。地声参数通常难以获取，故本文视其完全不确定，变化区间设置较大。同时，为满足沉积层参数与基底的相对特性，设置1<2<3依次增加，。

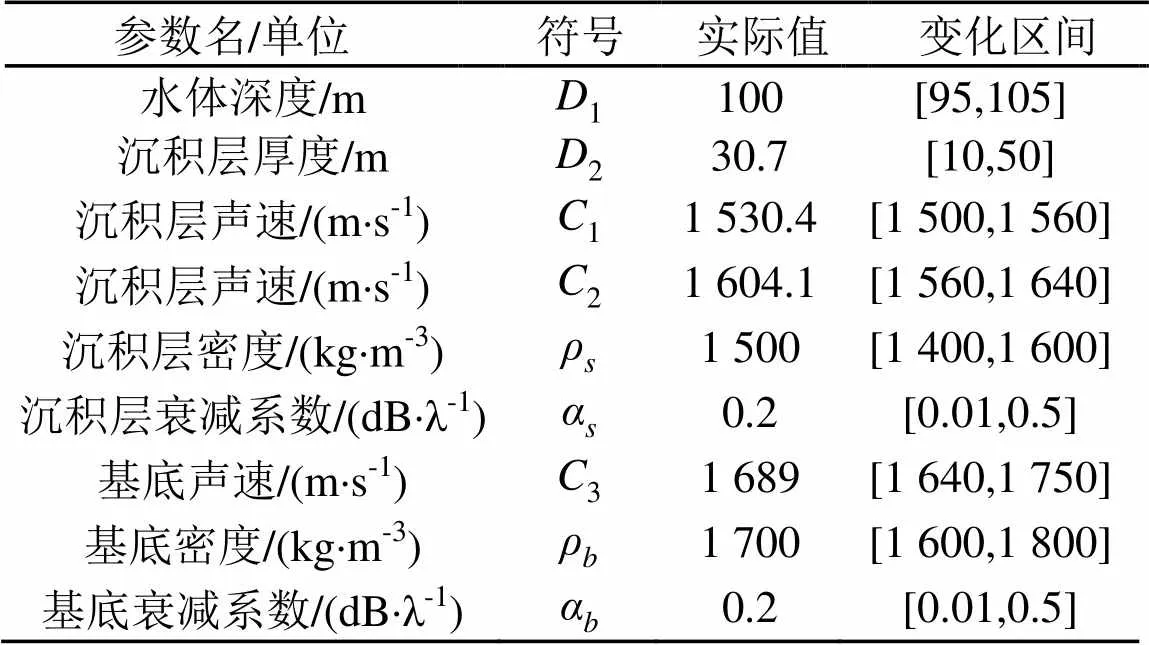
表1 Workshop’97浅海环境基准模型参数单位及取值

1.3 声场扰动指标

声压与相位特征是水声场扰动的集中体现，单纯的能量变化不能有效反映声场扰动，且单点声压不能体现出整个声场的变化性质。Bartlett处理器[4]常用于地声参数反演、声源定位：

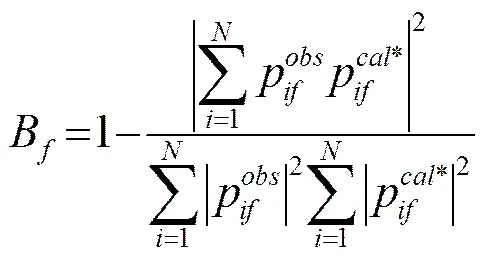
式(2)中，为垂线阵(Vertical Line Array，VLA)水听器的阵元数；为第个水听器频率为的模型计算声压值；原为实测声压值，本文将其定义为利用Workshop’97中各参数取实际值时，利用模型计算的声压值；“*”表示共轭转置。进而、的相关性最大似然函数可表示为

(3)

以似然函数为声场扰动指标，可有效研究近、中、远场不同深度处声压的变化特征，预报某一变量条件下的声场定量结果，给出该变量的变化区间及的概率密度特征，进而对比分析浅海环境下各参数随机变化时对声场扰动的影响。

1.4 MCMC方法

MCMC方法是随机模拟(又称统计模拟)方法的一种，用于重复多次随机抽取服从某种分布的样本，以模拟统计分析某随机事件出现的概率密度[18]，其主要思想包括马氏链、蒙特卡罗积分及M-H抽样算法。

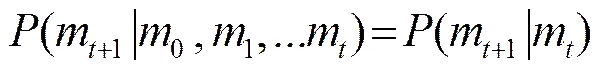
式(4)即为马氏链的基本原理，即任一时刻t+1的状态转移概率只与前一时刻相关，而与已生成的样本无关。随机抽取先验概率服从某种分布的海洋环境参数变量，生成易于实现且不可约遍历链，则的条件概率密度积分可表示为

(5)

式(5)中，为参数维度。当随机抽取样本达到一定数量时，蒙特卡罗积分可得到的一种无偏、非对称估计结果。

海洋环境各参数的不确定性强，各水声参数随机变化，在对各参数已知甚少的情况，可视其在某取值区间内服从均匀分布[19-20]，故可利用水声数值模型模拟水声场的概率密度特征。

2 声场扰动分析

设海水声速剖面在海面处(0 m处)声速值为1500 m/s，海底(1处)为1 480 m/s，声速向下均匀减小。单频150 Hz声源位于30 m深度处，VLA阵元数=19，分布于5～95 m间，垂向间隔5 m。取=30 dB，声场计算垂向步长为1 m，水平步长为10 m。各参数在其变化区间内随机均匀采样。

2.1 各参数的声场扰动敏感性分析

基于上文构建的Workshop’97水平不变海洋环境基准模型，采用单因子变量原则，分别采用1000次MCMC随机模拟统计各不确定水声参数(见表1)对声场的扰动。

概率密度函数(Probability Density Function，PDF)，在参数变化区间内分布越均匀，说明参数变化对Bartlett处理器的影响越小，即对声场扰动敏感性越低，反之则敏感性越高。

分析图2可知，参数1(图2(c))、1(图2(i))对声场扰动最敏感，PDF集中分布于实际参数值附近，呈明显的单峰现象；参数(图2(f))、(图2(g))的PDF在其各自的变化区间内几乎呈均匀分布，参数变化对声场扰动几乎无影响，即敏感性最低；参数(图2(a))、(图2(b))、2(图2(d))、2(图2(e))、3(图2(h))的敏感性居中。

分析图2中各子图中的A(近场)、B(中场)、C(远场)可知，参数、、、敏感性随距离的增加逐渐增强；、、逐渐减弱；、对声场敏感性弱，这里不作分析。

(a)α变化时的声场扰动概率密度函数  (b)ρ变化时的声场扰动概率密度函数   (c)1变化时的声场扰动概率密度函数

(d)2变化时的声场扰动概率密度函数  (e)2变化时的声场扰动概率密度函数   (f)α变化时的声场扰动概率密度函数

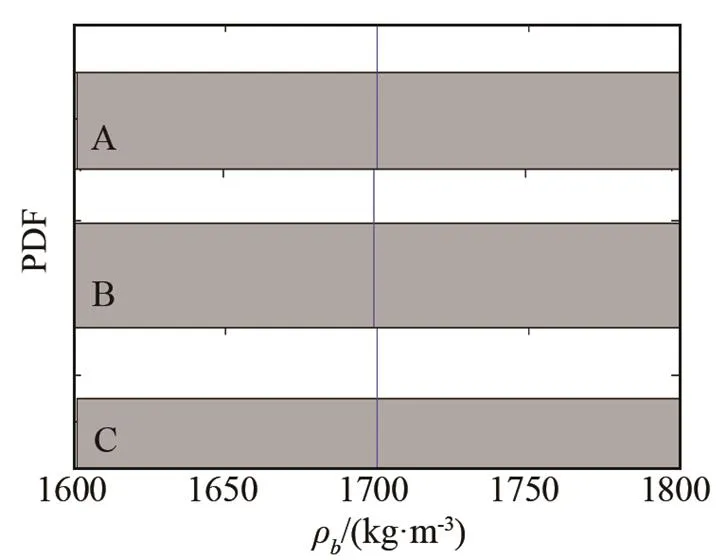
(g)ρb变化时的声场扰动概率密度函数   (h)C3变化时的声场扰动概率密度函数   (i)D1变化时的声场扰动概率密度函数

下边界对声场扰动的影响主要源于其边界反射及介质内的声能衰减。声波由声源产生，在近、中、远场传播过程中，边界反射损失()逐渐增大，

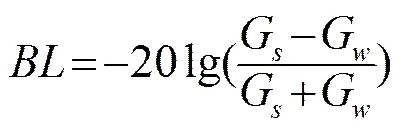
如图3所示，浅海环境中的声传播，声能随距离增加，进入沉积层内的部分逐渐减少。这是由于略射角较大的声波多次边界作用，衰减较快，中、远场处的声能主要由小略射角声波组成。随着传播距离增加，声能无法传播至沉积层下层及基底层，故沉积层的厚度、底层声速、基底层声速的声场扰动敏感性随着距离的增加逐渐减弱。

单凭图2中各参数PDF的定性分析，不能很好地对其声场扰动敏感性进行排序。作者通过获取各参数最大概率密度函数值(max(PDF)，=1,2,…,9)，统计得到PDF≥*max(PDF)的部分所占样本数的比例，如图4所示(=0.5)。比例越大，说明样本的PDF差异越小，敏感性越低。

(a) 近场(1 km)

(b) 中场(10 km)

依据图4(a)可将各参数近场声场扰动敏感性进行排序，近场按、、、、、、、、敏感性逐渐降低。然而各参数敏感性随距离变化差异较大。中场按、、、、、、、、敏感性逐渐降低(图4(b))；远场按、、、、、、、、敏感性逐渐降低(图4(c))。

2.2 各参数的声场扰动相关性分析

2.1节讨论了各海洋环境参数单因子变化时的声场扰动敏感性，实际上各参数间的不确定性对声场扰动存在一定的相关性，定义相关性矩阵[21]：

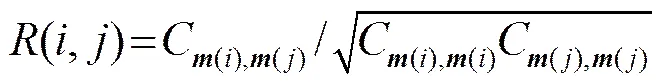
(8)

式(8)中，=1,2,…，为MCMC总的采样次数，为、条件下的条件概率，为第个参数的数学期望：

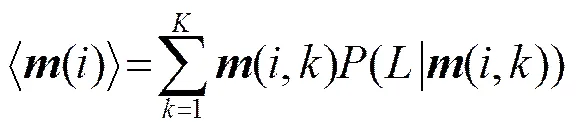
分别采用1 000次MCMC随机模拟并计算各不确定水声参数(见表1)两两间的相关性大小，见表2。

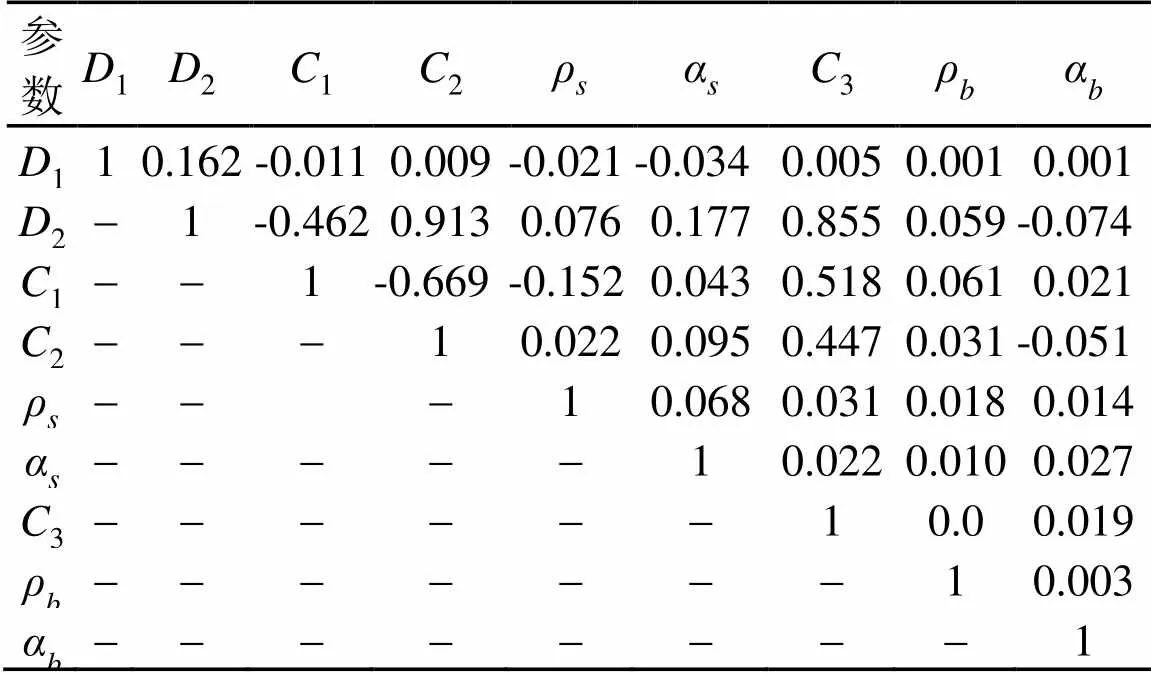
表2 Workshop’97浅海环境基准模型参数间相关性

事实上，本文利用Bartlett处理器计算相关性函数作为声场扰动指标，用以量化海洋环境参数的不确定性导致的声场随机起伏，主要是声压振幅与相位的匹配。各参数的随机变化所导致的声压差异较大，当某一参数增加(或减小)导致声场扰动较大时，另一参数减小(或增加)可减小声场扰动，说明这两个参数具有一定的负相关性。例如，1、2分别为沉积层上、下边界的声速，当1增加时，海水与沉积层间的声阻抗增加，导致进入沉积层的声能减少，从而导致似然函数减小(即声场扰动较大)；若减小2，则缩小了沉积层垂向声速差，使得更多的声能在沉积层内传播，进而使得似然函数有所增加，则说明1、2具有一定的负相关性。

3 结论

本文研究了多种环境不确定因素对浅海声场扰动的影响，给出了各种因素对声场扰动的敏感性大小及排序，并分析了不同因素将对声场扰动影响的相关性，得到结论如下：

(1) 浅海环境不确定因素对声场扰动的敏感性强度，近、中、远场存在一定的差异，大致可分为三个级别。其中，、对声场扰动最敏感，、、、、对声场扰动影响较小，、几乎无影响。

(2) 各环境参数对声场扰动的敏感性随距离变化差异较大，、、、敏感性随距离增加逐渐增强，、、逐渐减弱，这主要与声传播过程中的声压幅度与相位有关。

(3) 海洋环境参数之间对声场扰动的影响具有一定的相关性，、，、，、，、间存在较强的正相关性，、，、间具有显著的负相关性。

海洋环境不确定性来源多样，其中时空多变性，数据缺乏导致的未知性，实际操作及仪器设备本身精度都是不确定性来源。实际应用中应首先根据具体的海洋环境来确定水声参数的不确定性区间，进而重点考虑对声场扰动敏感性较强的参数及其之间的相关性。

[1] Cho C G, Song H C, Hodgkiss W S. Robust source-range estimation using the array/waveguide invariant and a vertical array[J]. J. Acoust. Soc. Am., 2016, 139(1): 63-69.

[2] 李倩倩, 李整林, 张仁和. 不确知海洋环境下的贝叶斯声源定位法[J]. 声学学报, 2014, 39(5): 535-543. LI Qianqian, LI Zhenglin, ZHANG Renhe. Bayesian localization in an uncertain ocean environment[J]. Acta Acustica, 2014, 39(5): 535-543.

[3] 过武宏, 笪良龙, 赵建昕. 地声参数及传播损失不确定性估计与建模[J]. 应用声学, 2015, 34(1): 71-78. GUO Wuhong, DA Lianglong, ZHAO Jianxin. Estimation and modeling of geoacoustic parameters and transmission loss uncertainty [J]. Journal of Applied Acoustics, 2015, 34(1): 71-78.

[4] Huang C F, Gerstoft P, Hodgkiss W S. Uncertainty analysis in matched-field geoacoustic inversions[J]. J. Acoust. Soc. Am., 2006, 119(1): 197-207.

[5] Sha L W, Nolte L W. Effects of environmental uncertainties on sonar detection performance prediction[J]. J. Acoust. Soc. Am., 2006, 117(4): 1942-1953.

[6] HE X Y, CAI Z M, LIN J Y, et al. The simulation research on forecasting the detection range of active sonar[J]. Journal of System Simulation, 2003, 15(9): 1304-1307.

[7] 潘长明, 高飞, 孙磊, 等. 浅海温跃层对水声传播损失场的影响[J]. 哈尔滨工程大学学报, 2014, 35(4): 312-318. PAN Changming, GAO Fei, SUN Lei, et al. The effects of shallow water thermocline on water acoustic transmission loss[J]. Journal of Harbin Engineering University, 2014, 35(4): 312-318.

[8] 笪良龙. 海洋水声环境效应建模与应用[M]. 北京：科学出报社, 2012. DA Lianglong. Modeling and application of underwater acoustic environment effect[M]. Beijing: Science Press, 2012.

[9] Harry D F. Predicting sonar performance using observations of mesoscale eddies[J]. J. Acoust. Soc. Am., 2006, 120(2): 3060-3069.

[10] Donald D R, Christopher F, Rowe M M. Effects of water-depth on matched-field localization in shallow water[J]. J. Acoust. Soc. Am., 1988, 83(6): 2180-2185.

[11] SHANG E C, WANG Y Y. Environment mismatching effects on source localization processing in mode space[J]. J. Acoust. Soc. Am., 1991, 89(5): 2285-2290.

[12] Kelvin R J, David R D. A method for approximating acoustic-field-amplitude uncertainty caused by environment uncertainty [J]. J. Acoust. Soc. Am., 2008, 124(3): 1465-1476.

[13] 赵航芳, 李建龙, 宫先仪. 不确实海洋中最小方差匹配场波束形成对环境参量失配的灵敏性分析[J]. 哈尔滨工程大学学报, 2011, 32(2): 200-208． ZHAO Hangfang, LI Jianlong, GONG Xianyi. Sensitivity of minimum variance matched-field beamforming to an environmental parameter mismatch in an uncertain ocean channel[J]. Journal of Harbin Engineering University, 2011, 32(2): 200-208．

[14] 王文博, 黄勇, 李淑秋. 水平不变浅海环境随机扰动水声场传播的影响[J]. 应用声学, 2015, 34(1): 90-94. WANG Wenbo, HUANG Yong, LI Shuqiu. Effects of random environment disturbance on sound propagation in range-independent waveguide in shallow water[J]. Journal of Applied Acoustics, 2015, 34(1): 90-94.

[15] Porter M B, Reiss E L. A numerical method for ocean-acoustic normal modes [J]. J. Acoust. Soc. Am., 1984, 76(3): 244-252.

[16] Tolstoy A, Chapman N R, Brooker G H. Workshop’97: Benchmarking for geoacoustic inversion in shallow water[J]. J. Comput. Acoust., 1998, 6(2): 1-28.

[17] Porter M B, A Tolstoy A. The matched-field processing benchmarking problem[J]. J. Comput. Acoust., 1994. 2(3): 161-185.

[18] 笪良龙, 黄海, 黄建波. Monte-Carlo方法在浅海声速不确定性研究中的应用[J]. 仿真火力与指挥控制, 2009, 34(2): 134-139. DA Lianglong, HUANG Hai, HUANG Jianbo. Simulation concerning application of Monte-Carlo algorithm to sound speed uncertainty of shallow sea[J]. Fire Control & Command Control, 2009, 34(2): 134-139.

[19] Peter G, Christoph F M. Ocean acoustic inversion with estimation of a posteriori probability distributions[J]. J. Acoust. Soc. Am., 1998, 104(2): 808-819.

[20] Stan E D, Micheal J W. Bayesian focalization: Quantifying source localization with environmental uncertainty[J]. J. Acoust. Soc. Am., 2007, 121(5): 2567-2574.

[21] Stan E D. Quantifying uncertainty in geoacoustic inversion. I. A fast Gibbs sampler approach[J]. J. Acoust. Soc. Am., 2002, 111(1): 129-142.

Analysis of acoustic field perturbation due to environment uncertainty in shallow water

GAO Fei, PAN Chang-ming, SUN Lei, GUI Fa-yin

(Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China)

Comparing the perturbation scale of underwater acoustic field due to environment uncertainty is of great theoretical significance and application value, which is important to improve the accuracy of underwater acoustic field prediction. In this paper, the likelihood function is constructed between the primary and perturbation sound field, which is used as the acoustic perturbation indicator. And, the numerical model of Kraken normal mode and the MCMC (Markov Chain Monte Carlo) method are used to analyze the acoustic perturbation and the correlation between different parameters, which result from the random variation of environment parameters, based on single variable principle and Workshop’97 shallow-water benchmark environment model. The results show that the parameters1and1are the most sensitive to acoustic perturbation, while theα,ρ,2,2,3are less, and theαandρare almost none of influence; The sensitivities ofα,ρ,1,1increase with distance increasing, while the sensitivities of2,2,3attenuate. It is found that reasonably strong positive correlations exist between2and2,2and3,1and3,2and3, and obvious negative correlations exist between2and1,1and2.

ocean environment uncertainty; acoustic field perturbation; correlations; likelihood function; Kraken model; Markov Chain Monte Carlo (MCMC) method

TB556

A

1000-3630(2017)-04-0309-06

10.16300/j.cnki.1000-3630.2017.04.003

2016-07-05;

2016-10-11

国家自然科学基金资助项目(41276088)、国家海洋公益性行业科研项目(2012050007-7)

高飞(1988－), 男, 湖南衡阳人, 硕士, 研究方向为海洋中尺度现象对水声传播的影响。

高飞, E-mail: gfei88_lgdx@163.com