基于Navier−Stokes方程幂律型浆液扩散压力

周子龙，杜雪明，陈钊，赵云龙

基于Navier−Stokes方程幂律型浆液扩散压力

周子龙1，杜雪明1，陈钊2，赵云龙1

(1. 中南大学资源与安全工程学院，湖南长沙，410083；2. 广西翔路建设有限责任公司，广西南宁，530029)

为了研究浆体在裂隙截面各处的压力分布规律和扩散半径，克服以往利用平均速度得到某一截面的平均压力的情况，达到较精确地控制浆体流向和扩散范围，基于黏性流体Navier−Stokes方程，对幂律流体在水平光滑裂隙管状模型内的扩散运动进行理论分析，重点讨论黏度系数、流变指数、注浆时间和裂隙高度方向的距离对注浆压力差和扩散半径的影响规律，从而为岩土裂隙的注浆设计提供必要的理论依据。研究结果表明：当黏度较小时，注浆的扩散半径较大，但当浆体黏度大到一定程度时，恒定注浆压力下容易产生压滤效应；当流变指数较小时，压力差∆无明显变化，超过某一特定值之后，压力差∆随着流变指数的增大呈现非线性快速增加；注浆压力在靠近流核区与非流核区界面的压力最大，随着逐渐远离流核区(方向)，其压力呈非线性逐渐减小，到达某一特定位置，然后迅速增大，但直至裂隙边界处其压力始终小于界面处的压力；随着注浆时间增大，浆液的扩散半径不断增大，并且呈现出非线性增大的趋势，但扩散半径的递增率逐渐减小，最终扩散半径趋于某一特定值。

幂律型浆液；Navier−Stokes方程；扩散半径；注浆压力；流变性

目前，人们对于岩土工程注浆浆液的研究主要侧重于注浆材料[1−3]，浆体性能[4−6]和设备等方面，而在注浆扩散理论方面的研究相对较少。由于缺乏有效的注浆扩散理论指导，在注浆过程中，注浆量、注浆压力以及注浆孔距和孔型一般都是根据经验和现场试验[7]等确定，不仅严重地影响了注浆效果，而且在一定程度上造成了地下水污染。为此，一些学者在注浆扩散理论方面进行了研究，如杨秀竹等[8−9]基于广义达西定律及球形扩散理论模型对宾汉浆体和幂律型浆体在岩土中渗透扩散半径的计算公式进行了推导，分析了浆体性能参数对注浆压力和扩散半径的影响；邹金锋等[10−12]对沿浆液扩散半径方向上的压力衰减分布规律进行了研究；章敏等[13]建立Herschel–Bulkley浆液扩散模型，对注浆时间、注浆压力、流变指数以及裂隙倾角等参数与注浆扩散之间的影响规律进行了探讨；李术才等[14]基于黏度时变性宾汉体本构模型，推导了C-S浆液在单一平板裂隙中的压力分布方程；张庆松等[15]通过开展水泥−水玻璃(C-S)浆液单一平板裂隙动水注浆模型试验，揭示了基于试验条件下的C-S浆液裂隙动水注浆扩散过程的扩散规律；刘健等[16]通过对比模型试验，对裂隙注浆扩散机制进行了探讨，研究了浆液在静水和动水中扩散规律。以往对注浆压力的研究主要是利用平均速度得出某一截面的平均压力的变化情况，实际上，同一截面上各处的压力变化情况是不同的，在特定情况下，利用平均值作为注浆参数会带来较大误差，同时，也不利于通过改变浆体微观特性来达到控制浆体扩散规律。为了更深入地研究浆液的扩散压力和半径的变化规律，从而精确地控制浆体流向和扩散范围，本文作者基于黏性流体Navier−Stokes方程，通过对幂律流体的本构方程理论分析，推导出幂律流体在裂隙管状模型中运动规律，重点分析浆体扩散半径和截面的压降分布规律以及浆体各参数对前两者的影响规律，以便为岩土裂隙的注浆设计提供参考。

1 注浆扩散模型的建立

1.1 基本假设

图1所示为浆液在假定的圆管裂隙中的扩散运动示意图。图1中：0为注浆孔半径；为圆管半径；为浆液流动速度；为浆液扩散压力；p为流核区半径。设圆管的半径，在注浆压力作用下，沿水平光滑圆管流动，取轴向方向为浆体的流动方向。本文为了定量地研究浆体参数如黏度系数、流变指数、注浆时间和裂隙高度等对注浆压力差和扩散半径的影响规律，特进行以下假定：

1) 浆液是均质的、不可压缩的流体，浆体的密度是常数，且忽略浆体自身的重力；

2) 浆液在扩散过程中无沉淀发生。

1.2 浆体压差分析

Navier−Stokes方程是流体力学中描述黏性流体的方程，其本构方程是：

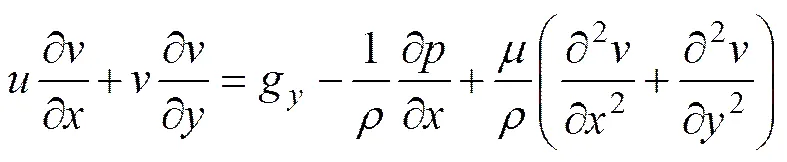
(2)

(3)

式中：为浆体在方向的速度；为浆体在方向的速度；g和g分别为重力加速度在坐标轴和方向的分量；为浆体流动方向所受的压力；为浆体的黏度；为浆体的密度。

假设浆体是二维水平流动，即=0；由于浆体在水平方向受到的压力远远大于浆体的自重，因此，可以忽略浆体的自重，由此可得：

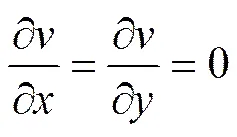
(6)

将式(4)~(6)代入式(1)~(3)经过化简整理可得

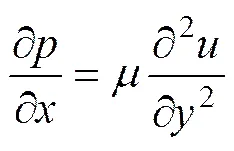
对式(7)中的变量进行积分可得到剪切率与压力梯度变化率的关系，即

(8)

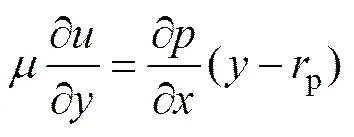
式中：p为流核半径高度，；，为浆液扩散的最大半径，为注浆孔的半径；为注浆的初始压力；c为注浆启动压力；为初始剪切力。幂律型浆体的本构方程为

(10)

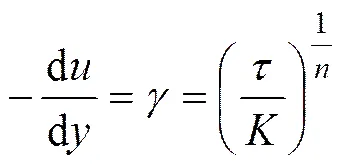
在不考虑其他外力作用下，根据图1结合流体受力平衡关系可得：

(12)

将式(11)和(13)代入式(9)，整理简化得出压力梯度的变化率，即

(14)

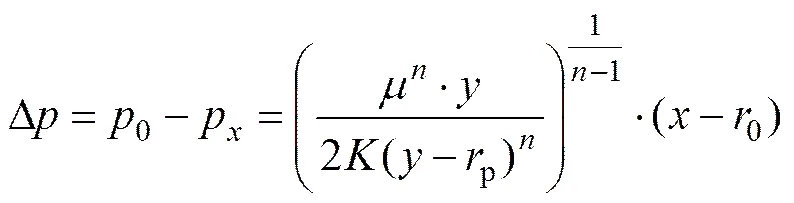
1.3 扩散半径分析

流核高度区域中的柱状浆体速度分布为

(17)

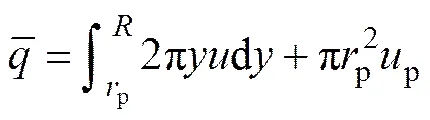
将式(16)和(17)代入式(18)经过积分简化整理得

(19)

根据单位时间注入裂隙的注浆量和扩散半径增大所需流量相等，可以得到注浆扩散半径，即

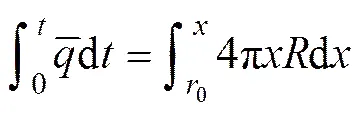
式中：为注浆时间。

对式(20)进行积分，同时考虑式(19)得出扩散半径与注浆参数的关系：

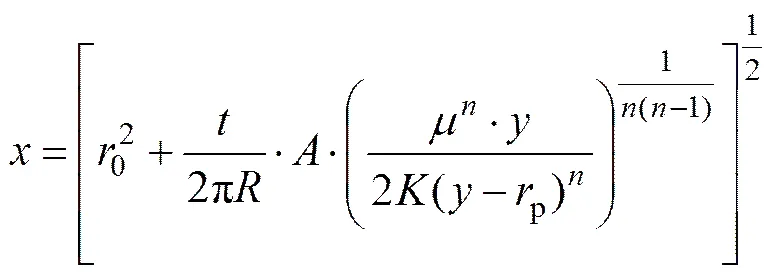
2 注浆压力差和扩散半径与浆液参数的影响规律

本文所研究的浆液符合幂律流体的流变特性，其注浆孔半径为0.025 m，本文取p为0.9×10−4m，岩土裂隙半径为1mm，其他参数则作为变量进行影响性分析。浆体黏度表征着浆体的流动性能，是由于浆体内部之间的摩擦而产生的，而稠度表征浆体软硬程度；在注浆的时间段内，浆体黏度对时间的敏感度远远比对稠度的大，两者之间没有特定的相关关系，假定稠度系数为某一定值，而黏度随时将发生变化，即取=2.32 Pa∙s。

当≤p时，浆体处于流核高度范围内，由于此区域不受剪切力作用的影响，因此，单位距离内的压力降可以近似为零，即流核区域内各个截面压力可以近似为注浆初始压力。本文主要讨论当＞p即浆体处于非流核区域时的扩散规律。

2.1 注浆压力降分布与浆体黏度参数、流变指数、裂隙高度以及扩散距离的影响规律

注浆压力差随扩散距离的变化规律如图2所示。由图2可知：在裂隙截面高度0.2­mm处，在同一黏度和同一流变指数下，注浆压力差随着扩散距离的增大呈线性增大。这是由于浆体在非流核区域内运动时，需要克服浆体内部的剪切力，同时浆体的流变性质和岩土介质的结构特征没有变化，因此，注浆压力随着扩散距离的增大呈线性减小。当＜1时，随着黏度增大，到达同样扩散距离所需压力也是增大的；当＞1时，压力差随着扩散距离的增大基本不变，近似于零。这是由于浆体黏度表征着浆体的流动性能，是浆体内部之间的摩擦剪切而产生的，黏度越大，受摩擦剪切所损失的能量越大，扩散到相同的距离所需能量也越大；当＞1时，浆体属于膨胀性流体，在注浆压力作用下，其黏度会因剪切速率的增大而增大，浆体的流动阻力很大，使浆液无法进入裂隙中，因此，在整个注浆过程中，压力差几乎为零，只有通过适当的办法迫使岩土介质产生较大的新裂缝，才可以发生浆液的扩散运动。

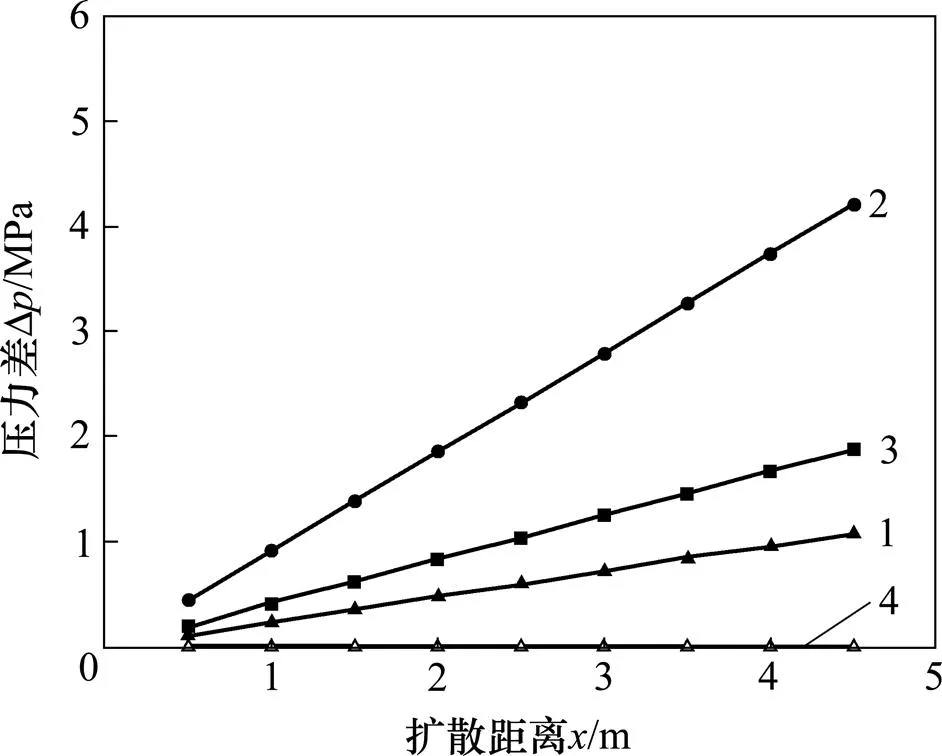
1—μ=0.08, y=0.2 mm, n=2/3; 2—μ=0.04, y=0.2 mm, n=2/3; 3—μ=0.06, y=0.2 mm, n=2/3; 4—μ=0.08, y=0.2 mm, n=3/2。

注浆压力差随流变指数的变化曲线如图3所示。由图3可知：当流变指数在0.1~0.4之间时，注浆压力差的变化比较缓慢；当流变指数超过0.4时，压力差随着流变指数的增大呈现非线性快速增加，并且黏度小的压力差的变化率比黏度较大的浆体压力差大。流性指数表征了该流体偏离牛顿流体的程度，当流变指数<<1时，浆液属于假塑性流体，此类流体的结构性较强，加力后不能立即改变其牢固的网状结构，它需要有一定的剪切应力才开始流动，此时需要较大的能量破坏流体的网状结构而做功，因此，压力差较小；当流变指数越接近1时，流体的性质越接近牛顿流体，其流动性较好，此时，随着流变指数的不断增大，浆体的表观黏度相对来说也会变小，产生的流动阻力也较小，要迫使浆体流动只需要克服较小的流动阻力做功即可，因此，压力差随着流变指数的增大而迅速增大。

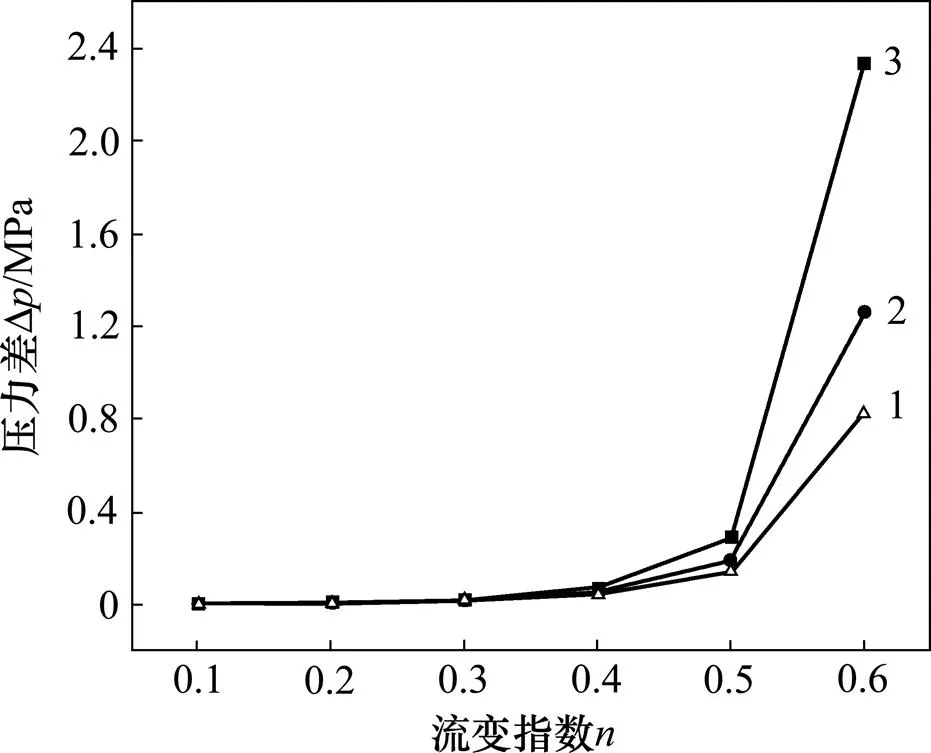
1—μ=0.04, x=2 m, y=0.2 mm; 2—μ=0.06, x=2 m, y=0.2 mm; 3—μ=0.08, x=2 m, y=0.2 mm。

图4和图5所示分别为注浆压力差随裂隙高度变化规律和分布图。由图4和图5可以看出：以上部的非流核区为例，注浆压力在靠近流核区与非流核区界面的压力最大，随着逐渐远离流核区(方向)，其压力呈非线性逐渐减小，到达某一特定位置，然后迅速增大，但是直至裂隙边界处其压力始终小于界面处的压力。造成此现象的原因为：流核区域内浆体内部的剪切力可以忽略不计，此区域内的注浆压力基本不变，2个区域界面处由于浆体发生相对滑动，需要克服浆体内部剪切力做功造成压力损耗不断增大；当到达某一特定部位时，随着裂隙高度不断增大，相当于裂隙空隙变大，同时，本文已假设浆体与岩土介质界面处不发生作用，不需考虑岩土介质与浆体之间的表面张力作用，浆体更易于在裂隙中扩散，相对于界面处压力损耗较小；浆体在扩散过程中，自始至终存在内部剪切摩擦损耗，裂隙边界处其压力始终小于流核区的 压力。

1—μ=0.08, x=2 m, n=2/3; 2—μ=0.06, x=2 m, n=2/3; 3—μ=0.04, x=2 m, n=2/3。

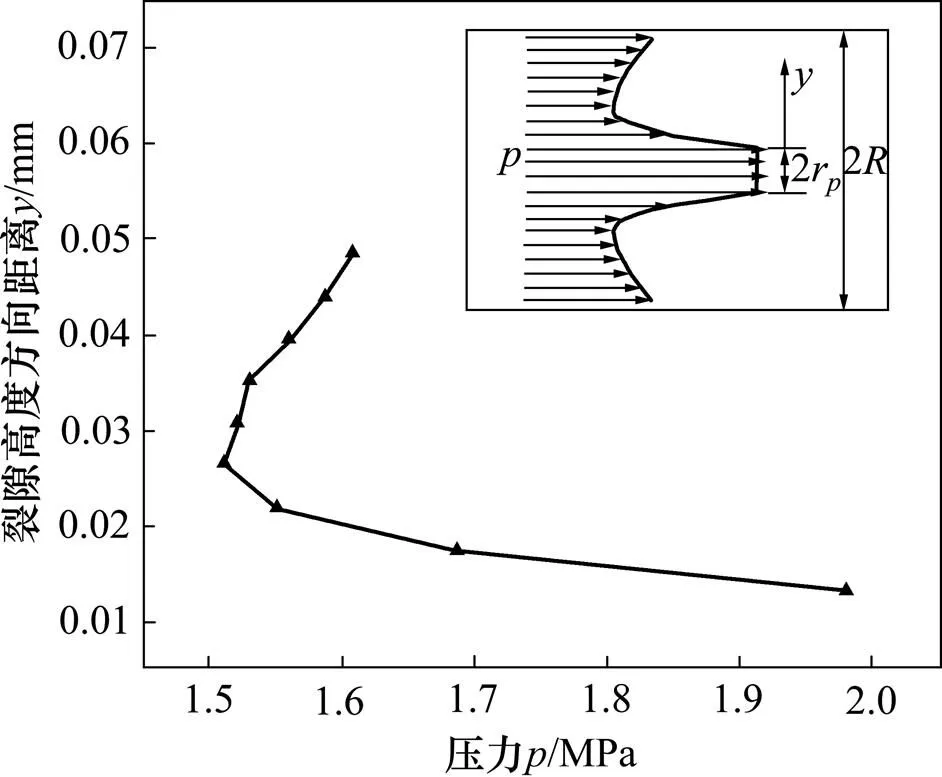
图5 裂隙高度方向的压力分布图

注浆压力差随黏度变化规律如图6所示。由图6可知：随着浆体黏度不断增大，到达相同的扩散半径所需的注浆压力也越大，最后趋于某一特定值；黏度越大，其浆体内部颗粒所占比例越大，则颗粒运动时发生的内摩擦阻力越大，发生流动所需克服的剪切变形阻力越大，注浆过程中损失压力能耗越大；当浆体黏度大到一定程度时，由于通过某一固定截面的颗粒较多，浆液不易在裂隙中扩散，此时在恒定注浆压力下会产生压滤效应，使浆体的黏度变小，注浆效果达不到设计要求；同时也验证了图3所示结论，即流变指数较小时，压力差的变化与流变指数关联性较小。

2.2 扩散半径与注浆时间和浆体黏度的影响规律

图7所示为注浆半径随注浆时间的变化曲线。由图7可知：随着注浆时间增大，浆液的扩散半径不断增大，并且呈现出非线性增大趋势，但扩散半径的递增率逐渐减小，最终扩散半径趋于某一特定值；当黏度较小时，注浆的扩散半径相对较大；当注浆压力保持恒定时，随着浆液扩散半径不断增大，压力损耗不断增大，迫使浆液扩散流动的压力梯度变小，直至注浆的压力梯度小于浆液在岩土介质中的启动压力梯度时，浆液停止流动。在工程实践中，注浆压力是恒定的，由于需要克服外力做功而损失能耗，因此，存在1个极限注浆扩散半径。

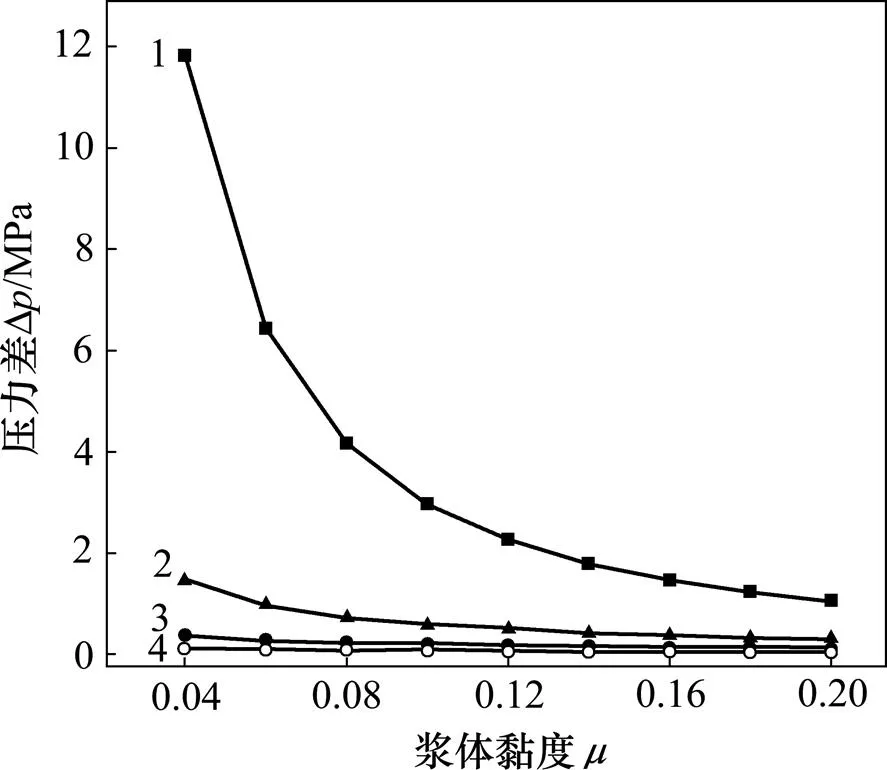
1—x=2 m, y=0.2 mm; n=0.6; 2—x=2 m, y=0.2 mm; n=0.5; 3—x=2 m, y=0.2 mm; n=0.4; 1—x=2 m, y=0.2 mm; n=0.3。

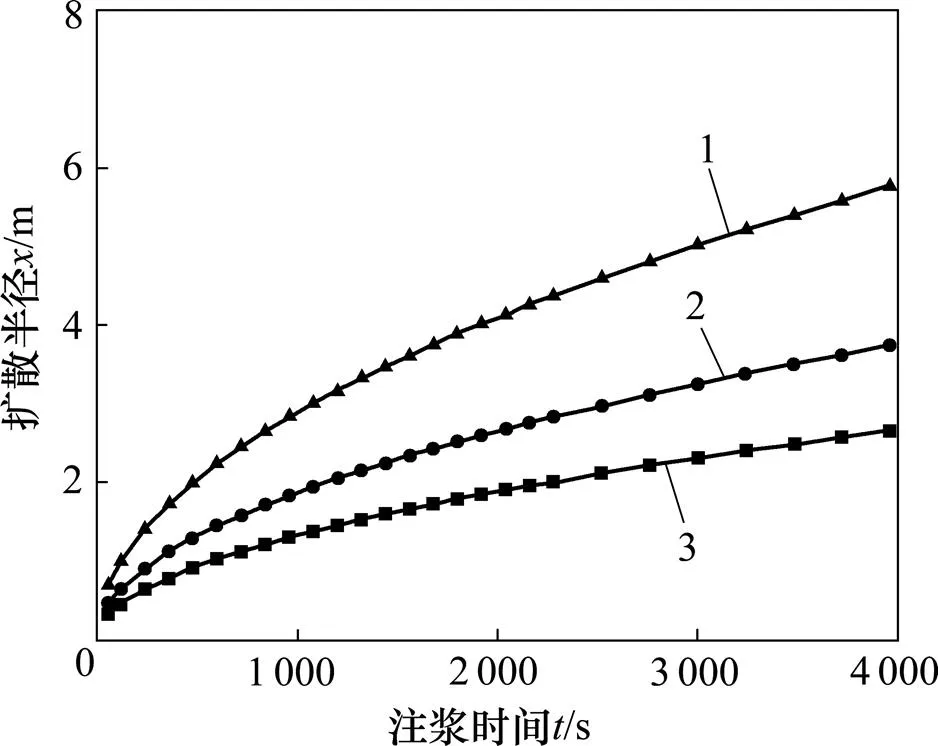
1—μ=0.06, n=2/3; 2—μ=0.08, n=2/3; 3—μ=0.10, n=2/3。

3 结论

1) 基于黏性流体Navier−Stokes方程，建立了针对幂律流体在水平光滑裂隙管状模型内的扩散的理论模型，探讨了黏度系数、流变指数、注浆时间和裂隙高度对注浆压力差和扩散半径的影响规律，可为注浆工艺参数的设计提供理论依据。

2) 当黏度较小时，注浆的扩散半径较大，但当浆体黏度大到一定程度时，恒定注浆压力下容易产生压滤效应，因此，在实际工程实践中，不能为了要达到注浆加固强度效果而不断增大浆体黏度，即使采用较大黏度的浆体也有可能达不到相应强度。

3) 注浆压力在靠近流核区与非流核区界面的压力最大；随着逐渐远离流核区(方向)，其压力呈非线性逐渐减小，到达某一特定位置，然后迅速增大，但是直至裂隙边界处其压力始终小于界面处的压力。通过添加某种外加剂可以减小其表面张力和剪切摩擦力，减少压力的能量损耗，更有利于浆体在裂隙中 流动。

[1] BORINAGA-TREVIÑO R, PASCUAL-MUÑOZ P, CASTRO- FRESNO D, et al. Borehole thermal response and thermal resistance of four different grouting materials measured with a TRT[J]. Applied Thermal Engineering, 2013, 53(1): 13−20.

[2] BORINAGA-TREVIÑO R, PASCUAL-MUÑOZ P, CASTRO- FRESNO D, et al. Study of different grouting materials used in vertical geothermal closed-loop heat exchangers[J]. Applied Thermal Engineering, 2013, 50(1): 159−167.

[3] DUAN H, JIANG Z, ZHU S, et al. New composite grouting materials: Modified urea–formaldehyde resin with cement[J]. International Journal of Mining Science and Technology, 2012, 22(2): 195−200.

[4] DAI H L, WANG X, XIE G X, et al. Theoretical model and solution for the rheological problem of anchor-grouting a soft rock tunnel[J]. International Journal of Pressure Vessels and Piping, 2004, 81(9): 739−748.

[5] CRISTELO N, SOARES E, ROSA I, et al. Rheological properties of alkaline activated fly ash used in jet grouting applications[J]. Construction and Building Materials, 2013, 48(11): 925−933.

[6] ROSQUOET F, ALEXISB A, KHELIDJB A, et al. Experimental study of cement grout: behavior and sedimentation[J].Cement and Concrete Research, 2003, 33(5): 713−722.

[7] 杨坪, 唐益群, 彭振斌, 等. 砂卵(砾)石层中注浆模拟试验研究[J]. 岩土工程学报, 2006, 28(12): 2134−2138. YANG Ping, TANG Yiqun, PENG Zhenbin, et al. Study on grouting simulating experiment in sandy gravels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2134−2138.

[8] 杨秀竹, 王星华, 雷金山. 宾汉体浆液扩散半径的研究及应用[J]. 水利学报, 2004, 35(6): 75−79. YANG Xiuzhu, WANG Xinghua, LEI Jinshan. Study on grouting diffusion radius of Bingham fluids[J]. Journal of Hydraulic Engineering, 2004, 35(6): 75−79.

[9] 杨秀竹, 雷金山, 夏力农, 等. 幂律型浆液扩散半径研究[J]. 岩土力学, 2005, 26(11): 112−115. YANG Xiuzhu, LEI Jinshan, XIA Linong, et al. Study on grouting diffusion radius of exponential fluids[J]. Rock and Soil Mechanics, 2005, 26(11): 112−115.

[10] 邹金锋, 李亮, 杨小礼. 劈裂注浆扩散半径及压力衰减分析[J]. 水利学报, 2006, 37(3): 314−319. ZOU Jinfeng, LI Liang, YANG Xiaoli. Penetration radius and pressure attenuation law in fracturing grouting[J]. Journal of Hydraulic Engineering, 2006, 37(3): 314−319.

[11] 张淼, 邹金锋, 陈嘉祺, 等. 非对称荷载作用下土体劈裂注浆压力分析[J]. 岩土力学, 2013, 34(8): 2255−2263. ZHANG Miao, ZOU Jinfeng, CHEN Jiaqi, et al. Analysis of soil fracturing grouting pressure under asymmetric loads[J]. Rock and Soil Mechanics, 2013, 34(8): 2255−2263.

[12] KELESSIDIS V C, DALAMARINIS P, MAGLIONE R. Experimental study and predictions of pressure losses of fluids modeled as Herschel–Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows[J]. Journal of Petroleum Science and Engineering, 2011, 77(3): 305−312.

[13] 章敏, 王星华, 汪优. Herschel–Bulkley浆液在裂隙中的扩散规律研究[J]. 岩土工程学报, 2011, 33(5): 815−820. ZHANG Min, WANG Xinghua, WANG You. Diffusion of Herschel–Bulkley slurry in fractures[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 815−820.

[14] 李术才, 刘人太, 张庆松, 等. 基于黏度时变性的水泥−玻璃浆液扩散机制研究[J]. 岩石力学与工程学报, 2013, 32(12): 2415−2421. LI Shucai, LIU Rentai, ZHANG Qingsong, et al. Research on c-s slurry diffusion mechanism with time-dependent behavior of viscosity[J] Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12): 2415−2421.

[15] 张庆松, 张连震, 刘人太, 等. 水泥−水玻璃浆液裂隙注浆扩散的室内试验研究[J]. 岩土力学, 2015, 36(8): 2159−2168. ZHANG Qingsong, ZHANG Lianzhen, LIU Rentai, et al. Laboratory experimental study of cement-silicate slurry diffusion law of crack grouting with dynamic water[J]. Rock and Soil Mechanics, 2015, 36(8): 2159−2168.

[16] 刘健, 刘人太, 张霄, 等. 水泥浆液裂隙注浆扩散规律模型试验与数值模拟[J]. 岩石力学与工程学报, 2012, 31(12): 2445−2452. LIU Jian, LIU Rentai, ZHANG Xiao. Diffusion law model test and numerical simulation of cement fracture grouting[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2445−2452.

(编辑 杨幼平)

Grouting pressure of exponential fluids based on Navier−Stokes equation

ZHOU Zilong1, DU Xueming1, CHEN Zhao2, ZHAO Yunlong1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. Guangxi Xianglu Construction Co. Ltd, Nanning 530029, China)

In order to study the pressure distribution and diffusion radius of slurry throughout fissure section, overcome the shortcomings that the average pressure of the fissure section was obtained by using the average speed, control the slurry flow and the range of diffusion accurately, the diffusion movement of exponential slurry in the horizontal fissures smooth tubular model was theoretically derived based on the Navier−Stokes equations of viscous fluid. Then the effects of law among the viscosity coefficient, rheology index, grouting time, the height of the fracture and diffusion radius or grouting pressure were mainly discussed, which provided theoretical basis for the grouting design of geotechnical fissure. The results show that when the viscosity is smaller, grouting diffusion radius is larger relatively. But the slurry viscosity reaches a certain degree, and the effect of filter is easy to occur under the constant grouting pressure. When the rheological index is smaller, pressure difference ∆has no obvious change. Exceeding a certain value, ∆shows a rapid increase of nonlinear along with the increase of rheological index.The grouting pressure of the interface between the flow core zone and non flow core zone is the maximum.The pressure shows a nonlinear decrease gradually away from the flow core zone (direction), and then increases rapidly. But the pressure value is always less than the pressure of the interface between the flow core zone and non flow core zone until the crack boundary. With the increase of the grouting time, the diffusion radius of grouting increases with the trend of the non-linear. However, the increasing rate of the diffusion radius is gradually decreased and the diffusion radius tends to reach a certain value finally.

exponential grout; Navier−Stokes equations; diffusion radius; grouting pressure; rheology

10.11817/j.issn.1672-7207.2017.07.020

TV139.16

A

1672−7207(2017)07−1824−07

2016−07−29；

2016−10−25

国家基础研究发展计划(973计划)项目(2015CB060200)；国家自然科学优秀青年基金资助项目(51322403) (Project(2015CB060200) supported by the National Basic Research Program (973 Program) of China;Project(51322403) supported by the National Natural Science Outstanding Youths Foundation of China)

杜雪明，博士研究生，从事采矿与岩土工程灾害防治研究；E-mail: 2007-dxm@163.com