石墨烯声子平均自由程随温度变化规律研究

任晓霞，贺长安，查小婷，周恩民，郑瑞伦



石墨烯声子平均自由程随温度变化规律研究

任晓霞，贺长安，查小婷，周恩民，郑瑞伦

（重庆文理学院 电子电气工程学院，重庆 402160）

考虑原子的短程相互作用和原子的非简谐振动，推导出石墨烯的声子平均自由程随温度变化的关系式，探讨了非简谐振动对它们的影响。结果表明：石墨烯的声子平均自由程随温度升高而非线性减小，温度低于20 K时，自由程随温度升高而急剧减小；温度高于300 K时，自由程随温度升高而减小的速度逐渐减慢；声子平均自由程随温度的变化率d/d均为负值，且随着温度升高而减小。在极低温条件下（<20 K），自由程的温度变化率随温度升高而变化很大，此后，变化速度逐渐减慢；与简谐近似的值相比，非简谐项引起的声子平均自由程及其变化率的差值均随温度升高而增大。

石墨烯；德拜温度；声子平均自由程；非简谐效应；原子短程作用；温度变化率

石墨烯由于具有优良的导电、导热等性能，在光电子器件、半导体器件等方面具有广泛的应用前景。国内外学者已对它的制备、性质和吸附特点等进行了不少研究，但研究较多的是电学性质方面，而对它的热力学性质研究较少，至于它的非简谐特征则才开始研究。对于非简谐特征明显而有重要应用价值的热膨胀现象，文献[1]用实验对其进行了研究，文献[2-6]采用不同的方法或理论对实验结果给予解释，其结果不仅都有不同程度的误差，而且只给出一个常量值，不能反映热膨胀系数随温度变化的规律。对另一个具有明显非简谐特征而有重要应用价值的弹性模量，文献[7]通过对杨氏模量进行计算，推知弹性模量与温度有关，但未给出随温度变化的具体变化关系。最近，作者在文献[8-9]中，在考虑到原子短程互作用和原子振动的第一、二非简谐项的情况下，用固体物理理论，研究了石墨烯的线膨胀系数、声子频率等随温度的变化规律，但未研究声子平均自由程这一重要的热力学量随温度的变化规律。最近，文献[10]对非简谐原子链中的声子平均自由程进行研究；文献[11]研究了缺陷类型和缺陷浓度对带有缺陷的石墨烯的声子平均自由程的影响；文献[12]由玻尔兹曼输运方程出发，采用变分法，研究了三维固体材料声子平均自由程的分布。鉴于石墨烯的这些物理量在理论和应用上的重要性，本文将用固体物理理论探讨它们的变化规律和原子非简谐振动的影响。

1 物理模型以及简谐系数和非简谐系数

本文研究的石墨烯是由个碳原子构成的二维六角格子平面系统，设平面为平面，轴垂直向上。文献[13]用哈里森键连轨道法，求出在未考虑短程相互作用情况下，一个原子的平均相互作用能。文献[14]进一步考虑到原子短程作用，将相互作用能写为：

式中：1为金属化能；2为共价能，它与原子间距离的平方成反比，可表示为：

原子在平衡位置附近作微振动，将()在平衡位置0附近展开，偏离很小时，有：

2 声子平均自由程随温度的变化

2.1 德拜温度随温度的变化

德拜温度D是晶格动力学中一个重要参量和特征温度，文献[15]给出简谐近似下德拜温度D0与简谐系数0和原子质量的关系为。这里B、分别是玻尔兹曼常数和普朗克常数，考虑到原子非简谐振动后，由文[16]给出的振动频率与温度的关系，可得到德拜温度随温度的变化为：

2.2 石墨烯的声子平均自由程与温度的关系

声子平均自由程为声子平均速度和弛豫时间的积，即[17]：

=（4）

式中：平均声速与纵声子对应的波速L和横声子的波速T的关系为：

石墨烯的声子弛豫时间随温度的变化，可由声子数分布()与弛豫时间的关系求得。结果是[16]非低温情况（>300 K），声子弛豫时间的倒数随温度的变化为：

低温情况（100~273 K），声子弛豫时间的倒数随温度的变化为

由（5）~（7）式求得声子弛豫时间随温度的变化，代入（4）式，得到石墨烯的声子平均自由程与温度的关系，结果是：非低温情况（>300 K），为：

低温情况（100~273 K），为

另外，文献[17]给出温度很低（10~100 K）时，声子平均自由程与温度的关系为：

这里是与物质有关的2~3之间的参数，0是待定参量，它可由某一温度下已知的热导率的值来确定。

3 石墨烯的声子平均自由程的温度变化率随温度的变化

声子平均自由程的温度变化率d/d的大小，反映了热传导的快慢。它可由（8）~（10）式求得，结果是：非低温情况（>300 K），为：

低温情况（100~273 K），为

极低温情况（10~100 K），为

4 非简谐振动对石墨烯声子平均自由程温度变化规律的影响

现讨论原子非简谐振动对石墨烯声子平均自由程随温度变化规律的影响。文献[13]给出：平衡时键长0=1.42×10–10m，|20|=12.32 eV，1=2.08 eV，而=10.08 eV·(10–10m)12。由这些数据代入（2）式求得0=3.538 8×102J·m–2、1= –3.497 25×1012J·m–3、碳原子质量=1.995 017×10–23g、2= 3.201 40 ×1022J·m–4，将、0以及玻尔兹曼常数B和普朗克常数一起代入（3）式，得到简谐近似下的德拜温度为常量D0=1 660 K。代入（3）式，得到石墨烯的德拜温度随温度的变化，结果表明：若不考虑非简谐项，则德拜温度为常量；同时考虑到第一、二非简谐项后，德拜温度随温度升高而缓慢增大，几乎成正比关系。还看出：本文由于考虑到原子的短程相互作用和原子的非简谐振动，不仅得到的结果比文献[15]的结果更接近文献[18]给出的实验值，而且还反映了石墨烯的德拜温度随温度的变化。在=300 K时的值与实验值相比，文献[15]的误差为12.15%，而本文的误差为10.75%。

文献[6]采用简正模式分解法，求出石墨烯的声子谱有2支，其中纵声子声速v=20.14 km·s–1，横声子声速=14.90 km·s–1，由（11）式求得平均声速=16.939 8 km·s–1。而0已由文献[19]给出=300 K时的热导率值5 000 W·m–1·K–1，可求得0=2.593×10–4m。将所求的0以及德拜温度D代入（10）~（12）式以及（13）~（15）式，得到极低温度（10~100 K）、低温情况（10~300 K）和非低温情况（>300 K）时的声子平均自由程及其随温度变化率d/d随温度的变化分别见表1、表2、表3。参考文献[20]采用简正模式分解法得到的弛豫时间和波速值，通过=计算出的平均自由程，在=300 K时的声子平均自由程及其随温度变化率d/d随温度的变化分别见表1、表2、表3。表中的“的值=1.7×10–9m和=1 000 K时的值=0.22×10–9m，与计算结果相吻合。

表1 极低温下声子平均自由程及变化率d/d随温度的变化

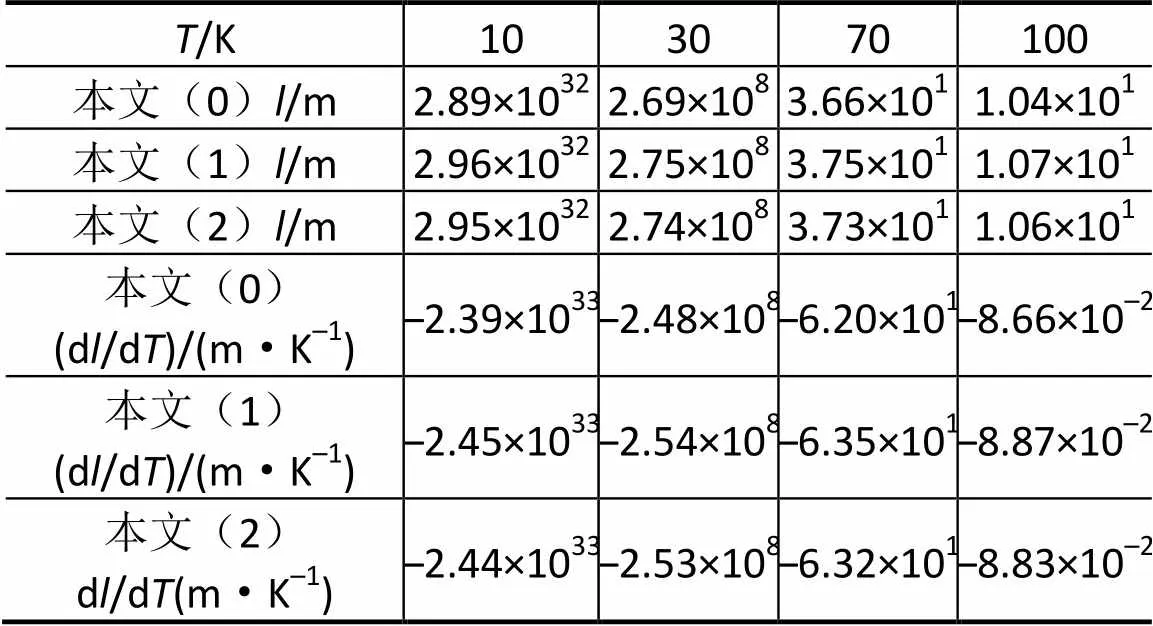
Tab.1 Changes of the phonon mean free path l and its changing rate dl/dT with temperatures in a range of very low temperatures

注：“本文（0）”是简谐近似的结果；“本文（1）”是只计及到第一非简谐项的结果；“本文（2）”是同时计及到第一、第二非简谐项的结果；表2，表3的含义与此相同。

表2 低温下声子平均自由程及变化率d/d随温度的变化

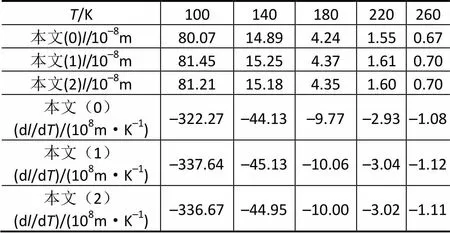
Tab.2 Changes of the phonon mean free path l and its changing rate dl/dT with temperatures in a range of low temperatures

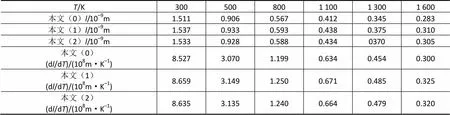
表3 非低温下声子平均自由程l及变化率dl/dT随温度T的变化

由表1、2、3的数据作出相应的变化曲线见图1、图2、图3。其中图中的（a）图是自由程随温度的变化；（b）图是自由程温度变化率随温度的变化；为了反映非简谐效应与温度的关系，（c）图和（d）图分别给出了计及非简谐项和简谐近似时的声子平均自由程差D=va–和自由程随温度变化率的差D(d/d)随温度的变化。图中的线0是只考虑简谐近似的结果，线1是计及第一简谐项的结果，线2是同时计及到第一、二非简谐项的结果。图1的“D1”表示第一简谐项与简谐近似的差值，“D2”表示第一、第二非简谐项与简谐近似的差值。

由图1、图2和图3的（a）可以看出，石墨烯声子平均自由程随温度的升高而逐渐减少。其中极低温下（<20 K），自由程随温度升高而急剧减小，温度每升高100 K时，自由程减小80%；此后，随着温度的升高，自由程减小的速度逐渐减慢，在低温下（100~300 K），温度每升高100 K时，自由程减小0.05%；非低温情况下，温度每升高100 K时，自由程则只减小0.000 5%。由图1、图2和图3的（b）可以看出，声子平均自由程的温度变化率为负值，温度较低时，随温度升高而变化的速度较快，而温度较高时，则变化较慢。由图1、图2和图3的(c)、（d）可以看出，与简谐近似的结果相比，非简谐效应引起的非简谐项和简谐近似时的声子平均自由程差D=va–和自由程随温度变化率的差D(d/d)均随温度的升高而增大，即温度愈高，原子振动的非简谐效应愈显著。由表3和图3看出，本文得到的结果与文[20]采用其他方法所得结果，有相近的数量级和相近的随温度变化趋势，这说明本文的合理性。

图1 极低温下石墨烯的声子平均自由程和变化率随温度的变化

图2 低温下石墨烯声子平均自由程和变化率随温度的变化

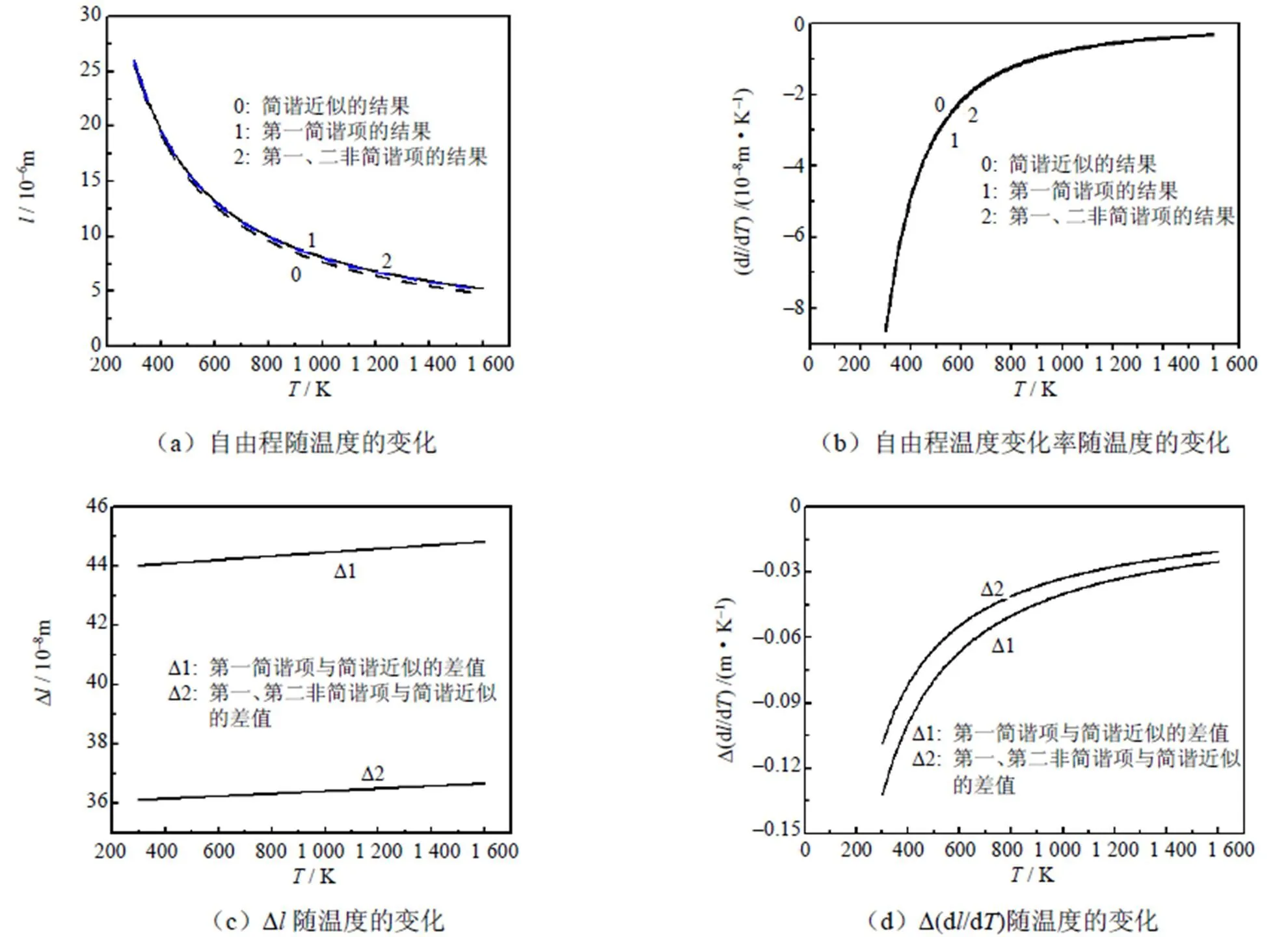
图3 非低温下石墨烯声子平均自由程和变化率随温度的变化

5 结论

本文对石墨烯的声子平均自由程随温度的变化规律进行研究，结果表明：（1）考虑到原子的短程相互作用和原子振动的第一、二非简谐项后，不仅所得到石墨烯的德拜温度与文献给出实验的值较接近，而且还给出德拜温度随着温度升高而缓慢增大，几乎成正比关系的变化规律；（2）石墨烯声子平均自由程随温度升高而减小，其中，在极低温（<20 K），自由程随温度升高而急剧减小；温度每升高100 K时，自由程减小80%。此后，随着温度的升高，自由程减小的速度逐渐减慢，非低温情况下，温度每升高100 K时，自由程则只减小0.0005%；（3）声子平均自由程随温度的变化率d/d随着温度升高而减小，极低温下（<20 K），自由程的温度变化率随温度升高而急剧减小。此后，随着温度的升高，自由程的温度变化率减小的速度逐渐减慢；（4）考虑到原子非简谐振动后，声子平均自由程小于简谐近似的值。非简谐项引起的自由程及其温度变化率的变化量D和D(d/d)均随升高而增大，温度愈高，原子振动的非简谐效应愈显著。

[1] BAO W, MIAO F, CHEN Z, et al. Controlled ripple texturing of suspended graphene and ultrathin graphite membranes [J]. Nat Nanotech, 2009, 4(9): 562-566．

[2] MOUNET N, MARZARI N. First-principles determination of the structural, vibrational and thermodynamic poperties of diamond, graphite and derivatives [J]. Phys Rev B, 2005, 71(20): 205214．

[3] ZAKHARCHENKO K V, KATSNELSON M I, FASOLINO A. Melting of graphene: from two to one dimension [J]. Phys Rev Lett V, 2009, 23(20): 1-4.

[4] JIANG J W, WANG J S, LI B.Thermal expansion in single-walled carbon nanotubes and graphene: nonequilibrium Green’s function approach [J]. Phys Rev B, 2009, 80(20): 205429．

[5] POZZO M, ALFE D, LACOVIG P, et al. Estimating anharmonic characteristics of single-sheet graphene at high temperatures [J]. Phys Rev Lett, 2011, 37(12): 1161-1164.

[6] DAVYDOV S Y. Estimating anharmonic characteristics of single-sheet graphene at high temperatures [J]. Tech Phys Lett, 2011, 37(24): 42-48(in Russian).

[7] SHAO T, WEN B, MELNIK R, et al. Temperature dependent elastic constants for crystals with arbitrary symmetry: combined first principles and continuum elasticity theory [J]. J Chem Phys, 2012, 137(19): 194901-1-194901-8.

[8] CHENG Z F, ZHENG R L. Study on the graphene of thermal expansion and deformation [J]. Chin Phys Lett, 2016, 33(4): 046501．

[9] 程正富, 郑瑞伦. 非简谐振动对石墨烯杨氏模量与声子频率的影响 [J]. 物理学报, 2016, 65(10): 104701-1-104701-8.

[10] SÄÄSKILAHTI K, OKSANEN J, VOLZ S, et al. Nonequilibrium phonon mean free paths in anharmonic chains [J]. Phys Rev B, 2015, 92(24): 245411.

[11] FENG T L, RUAN X L, YE Z Q, et al. Spectral phonon mean free path and thermal conductivity accumulation in defected graphene: the effects of defect type and concentration [J]. Phys Rev B, 2015, 91(22): 224301.

[12] CHILOYAN V, ZENG L P, HUBERMAN S, et al. Variational approach to extracting the phonon mean free path distribution from the spectral Boltzmann transport equation [J]. Phys Rev B, 2016, 93(15): 155201.

[13] DAVYDOV S Y. Estimating anharmonic characteristics of single-sheeting graphene at high temperatures [J]. Tech Phys Lett, 2011, 37(12): 1161-1164.

[14] DAVYDOV S Y. Energy of atoms in the fpitaxial graphene-buffer layer-SiC substrate system [J]. Phys Solid State, 2012, 54: 875-882.

[15] DAVYDOV S Y, TIKHONOV S K. 带宽半导体非简谐性质 [J]. 物理和半导体技术, 1996, 30(6): 968-973.

[16] 郑瑞伦. 胡先权固体理论及其应用[M]. 重庆: 西南师范大学出版社, 1996: 267-271.

[17] 沈从赴. 固体物理学基础教程[M]. 北京: 化学工业出版社, 2005: 245-249.

[18] LIKANOERROV S P, KAERGASOV B K. 晶体的弹性和形变特性 [M]. 莫斯科: 科学出版社, 1985.

[19] BALANDIN A A, GHOSH S, BAO W, et al. Superior thermal conductivity of single-layer grapheme [J]. Nano Lett, 2008, 8(3): 902-907.

[20] 孙旭东, 周明, 秦禄昌. 石墨烯结构与德拜温度因子的电子衍射分析 [J]. 电子显微学, 2013, 32(3): 206-210.

[21] 陆栋, 蒋平. 固体物理学[M]. 北京: 高等教育出版社, 2011: 91-93.

（编辑：曾革）

Temperature-dependent phonon mean free path of graphene

REN Xiaoxia, HE Chang’an, ZHA Xiaoting, ZHOU Enmin, ZHENG Ruilun

(College of Electronic and Electrical Engineering, Chongqing University of Arts and Sciences, Chongqing 402160, China)

By considering the non-harmonic effect and short-range interaction of atoms, the current work obtained the analytic functions of the graphene's phonon mean free pathdepending on temperature, and the influence of anharmonic vibration on them was also investigated. The theoretical results indicate that the graphene's phonon mean free path decreases nonlinearly with the increase of temperature. When the temperature is below 20 K, the free path sharply decreases with the increase of temperature. And changes become gradually slow at the temperature above 300 K. All relative change rate (d/d) of phonon mean free path is negative and decreases with the increase of temperature. The change rate of the free path sharply decreases with the increase of temperature when temperatures is below 20 K, then the changes gradually slow down. Compared with the results of the harmonic approximation, the anharmonic effects on phonon mean free path and its change rate become more significant with temperature getting higher.

graphene; Debye temperature; phonon mean free path; non-harmonic effect; short-range interaction of atoms; temperature change rate

10.14106/j.cnki.1001-2028.2017.01.005

TN604

A

1001-2028（2017）01-0027-06

2016-10-08

任晓霞

国家自然科学基金资助（No. 11574253）；重庆市教育委员会科学技术研究项目(No. KJ1601118)；重庆文理学院科技项目（No. Y2015DQ34）

任晓霞（1983－），女，山东烟台人，讲师，主要从事超级电容器器件及储能系统研究，E-mail:renxiaoxia7128@163.com 。

http://www.cnki.net/kcms/detail/51.1241.TN.20161230.1018.004.html

网络出版时间：2016-12-30 10:18:55