基于容迟网络模型的帆船VMG监测系统设计

林汉翔，李凌翎，任久春，朱 谦

(复旦大学 通信科学与工程系，上海 200433)

基于容迟网络模型的帆船VMG监测系统设计

林汉翔，李凌翎，任久春，朱 谦

(复旦大学 通信科学与工程系，上海 200433)

本文介绍了一种采用容迟网络模型设计的帆船运动多参数监测系统，以实现多节点的协同监测．利用排队论的理论方法，对系统牺牲实时性换取数据利用率、系统可靠性的性能进行了仿真分析，得出在资源受限的环境下(丢包率0.1)，容迟系统可以提高约17.3%的数据利用率，显著提高了监测结果的客观性．通过样机设备在实际训练中的使用，验证了该设计方法的可行性、可靠性．

协同监测； 容迟网络； 对地船速航迹速度； 排队论

随着物联网技术的快速发展，越来越多的行业提出了对信息化、数字化应用的需求．随着现代集成电路和微机电系统(Micro- Electro- Mechanical System, MEMS)传感器制造技术的进步，物联网通过互联的无线传感器网络(Wireless Sensor Network, WSN)感知并传递应用所需收集的信息，提高了人类对物理系统的管理与认知能力，进而推动了传统行业的现代化发展[1]．

在实际系统应用场景中，待观测现象往往需要多节点协同测量，以实现对观测现象更好地感知与理解[2]．于是，多传感器信息融合技术受到了广泛的关注．然而，无线传感器网络往往工作于资源受限的环境．这个特点使得异质数据源数据的汇聚与同步成为棘手的问题．尽管多传感器融合的概念很直观，但在具体实现方面仍存在诸多的困难．

从系统实际应用的实时性、可靠性和经济性等方面考虑，我们希望在可容忍的系统延时条件下，尽可能地改善数据对齐的处理过程，以期提高系统对残缺数据的利用率和计算结果的客观性、准确性，从而达到优化系统性能的目的．本文参考容迟网络中数据的“存储-携带-转发”机制，提出了一种在资源受限的工作环境下通过在汇聚节点提供数据携带缓存、设计数据重传的协议，以实现协同测量的优化方案，并基于该方案设计实现了一套用以监测帆船运动中对地船速航迹速度(Velocity Made Good, VMG)参数的系统．该系统是新一代的帆船多参数监测系统．上一代帆船多参数监测系统可对帆船的多项技术参数监测，但在数据同步汇聚及参数使用方面存在不足[3]．

本系统通过监测帆船的航速航向、船体姿态、赛场真风等参数，实现了对帆船运动核心参数VMG的最优估计，具有更高的实际应用价值；采用新的系统设计模型，实现了海上远距离通信环境下帆船运动各参数的容迟传输与同步汇聚．

1 容迟网络系统模型

如今，因特网协议与架构以其出色的性能、成熟的技术而广泛地发展出诸多出色的应用．不同于资源充分的因特网，有些网络在工作中缺乏“保持连接”的基础结构，而时常呈现出间歇性连接、延时明显、信号衰落显著的工作特点，需使用专有协议进行互联．于是国际互联网任务工程组(the Internet Engineering Task Force, IETF)针对这样的场景，提出了一种在端到端连接和节点资源都受限时适用的新型网络体系结构和应用接口，称为容迟网络(Delay- Tolerant Network, DTN)[3- 5]．

图1 传统因特网5层模型与DTN模型对比Fig.1 DTN model compared with traditional Internet five layers network model

DTN和传统因特网在分层体系结构上的对比，可用图1描述．可以看出，DTN相比于传统的五层网络模型，在应用层(Application Layer)与传输层(Transport Layer)之间加入了一个Bundle层(Bundle Layer)，以更好地体现它在这个6层模型中的作用．由于Bundle层的存在，DTN的整体工作机制通常被描述为“存储-携带-转发(store- carry- forward)”[4- 6]．

DTN一般有以下几个特性[5]：

1) 高延迟、低数据速率 端到端传输，具有较高的延迟总和，即每一跳上经历的链路传输时间、节点处理时间、传播时间以及排队时间等．容迟网络的数据传输速率一般在10kbps的数量级，延迟大约是1s或更长．

2) 数据流不对称性 由于数据负载在容迟网络内通常是不均匀分布的，因此双工信道的负荷是不对称的．通常容迟网络具有较大的下行净荷数据和上行控制数据．

3) 网络断开 端到端的断开比较普遍，原因有错误和非错误两方面．非错误方面，通常是因为移动、或者低占空比工作判定超时断开造成的．断开频繁地出现于容迟网络中，但是是可以预知的．

4) 长排队延迟 消息可能需要在中间路由节点中存储相当长的时间，以等待资源释放，或者发现更好的路径．

DTN模型被最为广泛地应用于星际通信、航空航天通信的系统设计中．无线传感器网络也是其典型应用领域之一．无线传感器网络呈现出容迟网络特性最直接的原因便是从能耗控制角度出发的系统设计方案．因为应用对节点提出的低功耗设计需求，节点间通信通常选择较低的发射功率，并低占空比操作．同时再加上应用中节点的移动性、恶劣工作环境给无线网络带来的多径衰落、阴影遮蔽等影响，节点工作过程中有很大概率呈现为“不可见”设备．这些特点使得无线传感器网络十分适合采用容迟网络模型来进行系统设计．

2 容迟监测系统模型

基于容迟网络模型而设计的无线传感器监测系统，其工作流程大致可分为原始数据采集、数据发送与汇聚、数据容迟计算3个关键步骤.

2.1原始数据采集

利用多种传感器技术，对待观测变量信息独立地感知、获取原始数据是各监测系统所必须的基础．传感器节点可将待观测的结果转化为可以进一步处理的电信号、或使用其他编码方式予以表征[7]．各传感器按照各自的采样率独立采集，也体现出了协同测量的工作模式．

对于已获取的原始数据，可采用一些数据滤波的方法在底层进行预处理．一些有代表性的物理量，如位置、速度、航向等，具有当前测量值与历史测量值存在延续性的特点，故可以考虑使用滚动平均的方法进行平滑处理，即计算当前时刻之前定长时间区间内该参数的平均值，以消除瞬时值可能存在的误差．同时，使用合理时间段内经过平滑处理的平均值，也比使用瞬时值更适用于引入了相对长的延时的容迟系统，可提高整个系统对待观测参量感知的客观性．

2.2数据发送与汇聚

各节点设备可调用各自的射频通信模块，向汇聚节点传输上述原始数据．在传输过程中，节点设备应提供该数据采集相应的时间戳信息作为汇聚节点数据同步的标识，可通过传输帧格式的协议设计实现．同时，传输过程不可预知地存在延时、丢包等现象，汇聚节点应可检测出数据丢失，并通知数据源进行重传．在等待重传的过程中，汇聚节点体现出了其在容迟网络体系中所独有的数据携带的功能，即Bundle层所起到的“store- carry- forward”的特性．

2.3数据容迟计算

对数据的容迟计算，是整个系统运行流程中最为核心的一步，同样在汇聚节点完成．

首先，汇聚节点应对缓冲区内的所有数据进行检验．对具有相同时间戳、且各数据源信息全部齐全的，将它们从缓冲区中提取出来，组成“有效数据组”，根据应用的实际物理模型进行相应的计算．而对于有数据残缺的，则在缓冲区内缓存，等待重传数据到来．

由于通常缓冲区使用的是微控制单元(Microcontroller Unit, MCU)的存储器，资源有限，因此不能无限长存储，需要汇聚节点对缓存数据进行管理．汇聚节点采用实时时间为动态门限，设置出动态更新的“等待窗口”．通过和数据的时间戳信息进行比对，尚处在有效窗口内有缺失的数据可继续缓存．如果重传信息在时间过期前到达，则该组数据仍然可完成组合并进行计算，弥补计算出该时刻待观测现象的结果并保存，体现出容迟计算的意义．若直到窗口关闭始终未能收到重传数据，则时间上过期的数据将清除出缓存区．

我们使用排队论理论模型作为预测工具，对系统性能进行估计．通过对数据的到达率与计算处理的服务速率进行合理的简化假设，分析求解出排队系统的队长和服务时间等参数，从而解决缓存应该设置多大的问题，并得到系统最优的滑动窗口大小[8- 9]．

3 实际应用场景简介

帆船运动是海上主流的竞技项目之一．根据航海学的黄金法则，VMG是衡量帆船向目标点移动能力的最直接参数，和比赛成绩的好坏密切相关[2]．为了提高运动员的训练水平和比赛成绩，通过科学仪器对帆船运动的多种技术参数进行监测，并合理建模以描述各参数对行船产生的具体影响，将帮助运动员更深刻地理解帆船运动，对提高成绩有直接的指导意义；同时教练员根据得到的信息也可以更加科学地执教、为运动员提供有针对性的训练．这些对于科学助力我国运动健儿在重大比赛中获得好成绩具有切实有效的意义．

VMG容迟监测系统从整体上划分为帆船端和教练艇端2部分(图2)．实际部署传感器并实施监测的帆船型号为激光雷迪尔级帆船．如图2所示，分别部署在帆船和教练艇上的传感节点独立采集各参量的原始数据，并发送至汇聚节点计算．系统中，带LCD显示屏的姿态测量节点(数字1标注设备)和帆船网关(数字2标注设备)组成帆船侧子系统；教练艇上由教练艇网关(数字3标注)和智能手机终端(数字4标注)组成应用子系统．

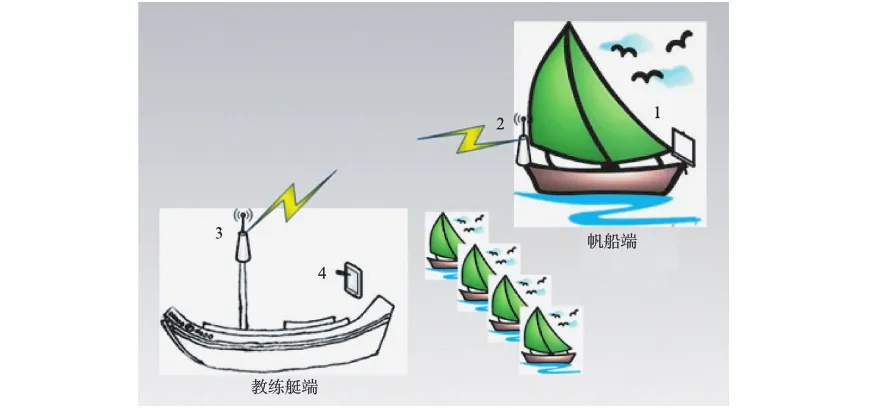
图2 VMG容迟监测系统示意图Fig.2 VMG delay monitoring system diagram

依照容迟网络的分层模型，VMG系统节点设备功能框图3(见第82页)所示．

图3将每一个设备按模块划分，各模块所实现的功能按照容迟网络分层模型结构表示出来，并使用了不同的颜色相互区分．各颜色与相应层对应关系为： 蓝色——感知层、黄色——传输层、红色——Bundle层、绿色——应用层．该结构框图详细地描述出了各个模块内部分工，将节点间对等通信的相应模块展示了出来．同时图中虚线标识出了整个系统应用中的数据流．整个系统按照上述容迟网络中的监测系统模型设计，由原始数据的采集开始，经过帆船网关上的汇聚、容迟计算后，再将结果分发至应用端，完成VMG监测的完整流程．

图3 VMG系统节点设备功能框图Fig.3 VMG monitoring system node functional block diagram

4 基于排队论的系统仿真

4.1模型构建

根据经典排队论模型，为VMG监测系统所搭建的排队论模型如图4所示．图中方框代表了系统中的帆船网关设备，共有来自3个数据源的数据在这里汇聚．图中用标有“g”的数据块代表倾角仪姿态数据；“GPS”数据块代表航速航向数据；“W”则代表教练艇网关发送来的真风数据．实际测量过程中，规定倾角仪姿态数据以及GPS模块的采样速率同为1次/1s；而来自教练艇网关的风速数据因信道容量限制而设置为1次/2s．图中以时间为坐标轴，用6组示例数据将3个数据源数据在到达时间上的关系简单表示出来．用相同的颜色代表具有相同时间戳标记的数据，红色为先，白色为最后到达的数据．参考排队论的理论模型，将系统看作提供服务的主体，数据则为需要系统提供服务的“客户”．帆船网关的两项计算转换任务便为具体的服务．图中用服务A代表姿态计算，服务B代表VMG参数计算．需要声明的是，由于风速数据为1帧/2s，我们认为该值可作为2s内风速风向的有效值．因此每收到一个新的风速数据，使用它与当前和下一秒的其他数据组成两组有效数据队．这也就是图中1帧风速数据同时作为红黄(或蓝绿)数据块中有效值的原因．

图4 基于排队论的帆船网关数据容迟汇聚、计算模型示意图Fig.4 Sailing gateway data’s delay convergence and calculation model diagram based on the queuing theory

可以看出，数据在到达系统之后，会先进入缓存区进行数据完整性的检验．若3个数据源具有相同时间戳的数据均成功到达，如图中红色、黄色和蓝色标识的情况，则称为通过检验的有效数据对，可以进入系统接受服务．若未通过检验，则需进入图中棕色区域标识的“时变滑动窗口数据携带区”进行暂存，等待缺失数据重传．时变滑动窗口的含义是，以固定时长作为窗口大小，根据实时时间动态改变上下有效界．若重传数据的时间戳落在了有效窗口内，如图中浅绿色所标记的“g”数据，则可补充为有效数据对，离开携带区前往服务队列．若携带区内暂存数据的时间戳已落在有效窗口之外，这些数据则被丢弃以释放携带区资源，重传的数据也无法继续接受服务．以上便是模拟数据在帆船网关进行汇聚、容迟计算的基本模型．

我们使用排队论模型来解决这种对象随机到达，且需排队接受服务的问题[8]．系统中数据缓存区实际使用了MCU单片机的片内存储器，需设置滑动窗口对缓存区内残留的缺失数据进行实时管理．滑动窗口设置过大，可能使得多个缺失的数据占满缓存区而造成新数据的丢弃；而窗口设置过小，则只能提供较短的容迟时间服务，可能导致数据丢弃，利用率下降．

根据排队系统模型，我们从数据输入、排队和接受服务3个过程，先对系统进行一些简化假设，以便分析．根据系统中数据的到达率、服务率等基本参数，我们可以从统计意义上计算出排队系统的利用率、平均队长等性能参数，进而得到在满足我们期望的性能条件下系统中的最大停留对象数．由此便可以指导我们设计系统的最佳窗口大小.3个过程分别描述如下：

1) 输入过程

系统中数据采用定时发送的方式，到达服务系统的过程服从马尔可夫过程．由于无线网络传输信道的衰落、多径时延与环境干扰等因素的影响，接收端实际收到数据不可避免地具有不可预测的时延．因此我们假设数据到达服务系统的过程服从泊松分布[8]，并带有一定的丢包率．

2) 排队规则

服务系统为到达数据开辟统一的队列，采用先到先服务的规则．所有数据均按照到达时间先后填入缓存区．符合条件的数据对将离开队列接受服务，而成分残缺的数据将滞留在缓存区内等待重传，并在滑动窗口判定为过期后被清除．

3) 服务过程

帆船网关内服务的过程主要由等待全部数据到达以通过数据完整性检验、执行计算、计算结果存储和结果传输至通信模块4部分组成．根据经典排队论模型，这里我们还需要假设服务时间是服从负指数分布的[8]．

在上述假设基础之上，我们为帆船网关建立了数据到达服从泊松分布、服务时间满足负指数分布的M/M/1/N/∞排队模型．N代表系统容量，∞则代表数据总量为理想状态下的无限量．我们用λ代表数据的平均到达率，μ代表平均服务率．则在系统容量为N的N个状态空间中，稳态下有如下系统状态平衡方程：

(1)

由状态方程，所有状态概率和为1的条件下，可解得系统的各状态概率解：

(2)

(3)

系统中存在3个数据源，且到达均服从泊松分布．其组成有效数据对的过程即为一定丢包率条件下3个数据源数据平均到达率之和．我们假设经无线发送的数据，存在ξ概率的丢包率(0≤ξ<1)．而认定与MCU电路直连的数据为理想信道，视为0丢包率．则有在不接受重传的模型中，系统有效数据对的平均到达率λ=3(1-ξ)2．而接受重传的模型中，我们假设重传数据同样满足在丢包率为ξ的信道中传输，则系统中有效数据对的平均到达率：

λ=3[(1-ξ)2+2ξ(1-ξ)2+ξ2(1-ξ)2]=3(1-ξ2)2.

(4)

再来讨论服务器的性能．

首先，我们可以将完成服务所需要的时间拆解为：

tserv=trec+tcalc+tstore+ttran,

(5)

其中：trec代表数据接收齐全的时间，以此作为数据组成有效对所需等待的时间；tcalc是系统计算处理时间，tstore是利用SPI接口向SD存储卡传输存储结果的时间；ttran则指代将结果经UART接口发送给通信模块的时间．由于我们使用了DMA的方式将数据填入UART接口的发送缓冲，因此可以认为向蓝牙模块和向Sub- GHz模块提交数据是并行的，ttran选取两者之间的较大者．

根据平均服务率的概念，由于系统服务的数据为3个，即有效数据对有3个成员，所以得出系统的平均服务率为：

(6)

根据理论推算及实验室部分实验测试，得到和服务时间相关的各参数如下： 由于GPS模块通过串行通信接口与MCU物理直连，因此可认为等待数据齐全的时间，即真风数据与倾角仪姿态数据接收的平均间隔．我们以真风数据到达时刻为基准，选取时间差最小的姿态参数配对，则有最大间隔时间为0.5s．假设数据发送是均匀分布的，因此可得平均间隔时间E[trec]为0.25s．数据计算的时间可忽略，即tcalc≈0．SD卡基础响应时间为20ms，存储使用SPI接口，速率为250kb/s,按照SD卡存储格式存储帧长96bit，则有tstore≈0.02+96×8/(250×103)=0.023s．2个UART接口统一采用9.6kb/s的波特率，传输帧长度为(37+60)bit，计算出传输完毕时间ttran=0.101s．所有参数相加，我们得到E[tserv]=0.25+0+0.023+0.101=0.374s．

根据式(4)与(6),计算得μ=8.021．假设丢包率为ξ=0.05，λ=2.985,则容迟系统的ρ=λ/μ=0.372．

根据系统状态概率分布公式：

(7)

我们所关心的最优窗口大小问题，可等效于求解联合概率密度可满足我们对系统性能期望的系统中对象个数．假设我们期望成功计算出VMG与姿态结果，存储入SD卡的结果数据丢包率小于0.01,即

(8)

将式(8)展开为累加的形式，运用等比公式有：

(9)

其中mr(y)代表的是99%的情况中，系统内最多的对象数，也即我们必要开辟的最短队长．等式两边取对数后，有：

(10)

当ξ=0.01时，mr(y)为3.681；ξ=0.1时，mr(y)为3.590．mr(y)在这里所代表的意义为： 根据排队论的理论指导，系统工作的99%的时间中是不会停留超过3.657个对象的，即4s前的数据99%以上的概率已离开系统．因此，我们根据这个参数，可以设置动态的时间窗口大小为4s．如果4s之后队列里仍残留有等待重传数据到达的残缺数据，则可视为重传数据不可达，对该组数据执行丢弃．

4.2Simulink工具箱下的动态仿真

我们使用了Matlab中的Simulink工具箱，对VMG容迟监测系统进行了动态建模．利用仿真结果，我们可以对系统性能有大致的评估．对于一般条件下的排队问题，解析解获取有相当大的难度．一个常用的做法就是用Monte Caro方法[10]，从统计试验的角度，将问题简化，求出象征系统性能的几个核心参数，如到达时间、服务时间、系统利用率等．

见图5，我们使用了工具箱中子库的各模块来模拟，按照上述数据传输关系设定了数据产生模块、运算模块并用连接线连接，将系统原始数据采集、数据同步计算的模型建立了起来．

首先，我们使用了均匀分布随机数发生模块作为模拟数据源，根据变换公式：

(11)

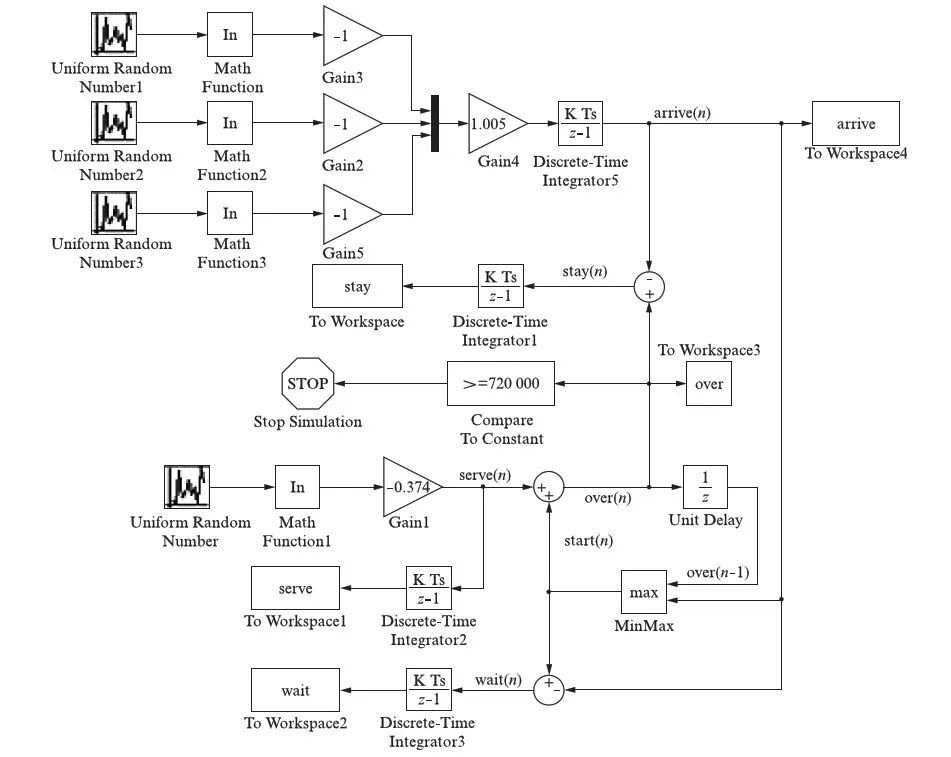
图5 使用Simulink工具箱对系统建模、仿真模型图Fig.5 System modeling and simulation model diagram using the Simulink toolbox

我们将均匀分布的u～(0,1)转换为了服从参数为λ的指数分布的随机数x．图中的ln模块，即求指数模块；三角形的增益模块则提供-1的相乘因子.3个模块相结合，我们便模拟出了定时发送，到达时间呈负指数分布的3个独立传感器数据源．

3路模拟信号通过信号组合器Mux组合成向量形式，以代表有效数据对．有效数据对的生成率，即具有相同时间戳的数据齐全通过检验的概率．我们再通过一个增益因子来模拟检验的过程，该增益因子与无线信道的实际丢包率相关．在图5所示例子中，我们选取了丢包率ξ=0.05的信道条件，则根据式(4)对应的数据到达率λ即为0.995，其倒数1.005即为信号的增益因子．我们为3个数据源设置了各不相同的随机数生成种子，以模拟3个数据源相互之间的完全独立性．

通过离散时间积分器(K Ts/z-1模块)，我们将数据到达时刻之间的间隔累加，从而得到了实际时间轴上各数据对到达的时刻arrive(n)．图中离散时间积分器还用于计算了数据在系统中等待的总时间wait(n)，数据在系统中停留的总时间stay(n)，以及我们最关心的系统提供计算服务的总时间serve(n)．我们使用4个To Workspace模块，以将这些仿真结果在Matlab控制台中输出．

排队系统的服务端，由上一节描述的模型，采用服务率为μ的负指数分布的数据源来代表服务的生成．我们用start(n)来代表服务开始时刻．服务开始时刻取决于： 无排队数据情况下等待下一个数据到来；已有排队数据情况下等待上一个服务结束．故使用求最大值函数表示start(n)，即：

(12)

其中，我们用了延迟模块，来移位提取出上一次数据计算结束的时间over(n-1)．有了服务开始时间后，服务结束时间和等待时间也就顺次而出了：

(13)

(14)

系统的整体运行参数上，我们设置系统仿真时间不超过720000s以保证收敛性．当over(n)的时刻达到时便执行停止步骤，此时系统会自动将仿真总步数输出到Workspace中，该步数意义即为实际接受了服务的对象数，对应到我们的系统模型中即有效数据对的生成个数．仿真结果如图6所示．

图6 Simulink仿真运行结果示意图Fig.6 Simulink simulation result diagram

我们在实验中，分别对丢包率为0.01，0.05和0.1的3种情况进行了仿真．而同时通过修改有效数据生成对增益，则可就有容迟系统与不提供容迟服务的2种系统均进行模拟．结果如表1所示．

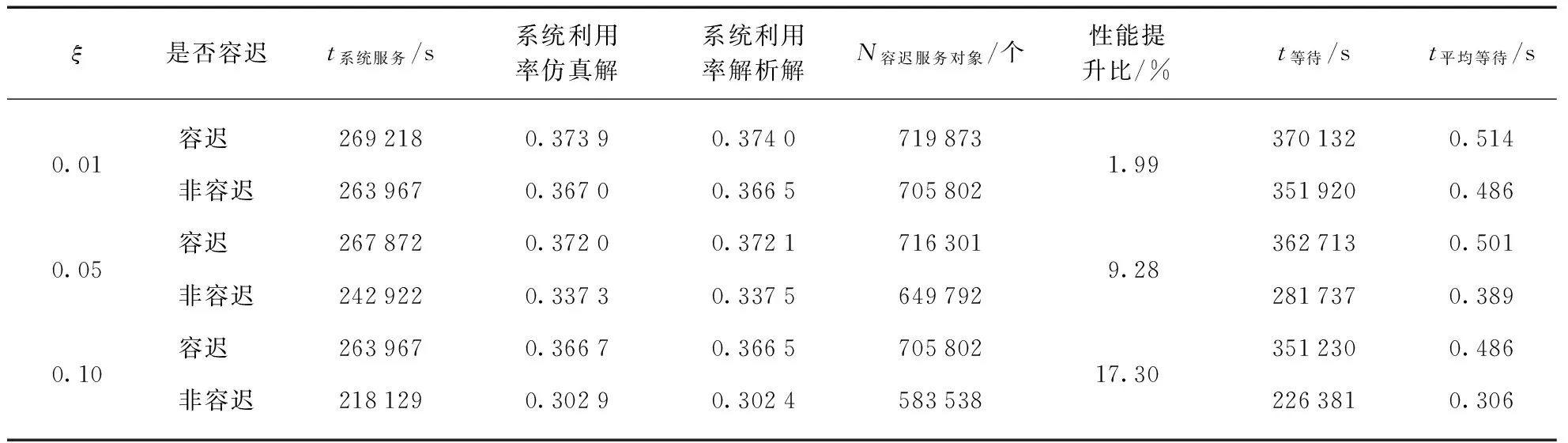
表1 不同丢包率下Simulink对VMG监测系统仿真结果(t总=720000s)

由仿真结果，我们可以得出以下几个结论：

1) 在各仿真情况中，系统的总运行时间是720000s．系统服务时间与总运行时间的比值，就是系统的利用率．可以看出利用系统仿真获得的结果，与使用理论公式推导得出的解析解相差很小，吻合度很高．在对系统利用率ρ的求解上，仿真解与解析解的最大误差在0.2%．可以认为，该仿真较贴切地模拟出了我们为系统构建的状态模型．

2) 通过将相同参数下采用不同机制的系统进行对比，我们可以看到： 采用容迟机制的系统，在服务对象上明显比将残缺数据直接丢弃的无等待服务提高了许多，且效果随环境恶劣程度而会更佳显著．在良好工作环境下(低丢包率)系统可以提高约2%的数据利用率，而在较恶劣的工作环境下(高丢包率)，容迟系统可以提高约17.3%的数据利用率．这意味着在资源受限的海上工作环境中，容迟系统将比即时系统带来十分明显的性能优化．

3) 从对象平均等待时间上，我们也可以看到为了提高数据的利用率，容迟系统中顾客的平均等待时间有明显延长．显然实时性与更高的数据利用率是一对相互权衡的指标．

5 结 语

本文提出了一种使用容迟网络模型进行无线传感器网络监测系统设计的方案，旨在解决资源受限网络工作环境中，多节点协同测量时所需解决的数据传输与同步汇聚问题．利用排队论方法所提供的理论依据，对模块的性能进行了整体分析，并结合无线网络中数据报文到达的随机性以及无线信道数据传输存在一定的丢包率的实际应用情况，运用Matlab工具进行了模拟系统的仿真，并与传统系统相对比，客观评估了系统的性能，明确了使用容迟网络模型进行系统设计时较传统设计方法所带来的收益与优势．

根据该设计方法，我们设计并实现了一套可实际应用的帆船运动中VMG参数的容迟监测系统．从应用需求分析出发，建立计算模型并确定待测物理量，通过优化设计双向的数据流，实现了对VMG参数的协同监测、容迟处理以及同步计算．目前本系统服务于市水上运动中心，通过样机在实际环境中的应用测试，证明了该系统方案设计的可行性，可靠性．

[1] 蒋春雨，肖 远，侯跃军，等.基于物联网无线传感网络的多传感器多参数协同监测研究[J].低碳世界, 2015(5)： 47- 48.

[2] 王耀南，李树涛.多传感器信息融合及其应用综述[J].控制与决策，2001，16(9)： 518- 522.

[3] 苏 菲，尚德重，汪建波，等.基于MEMS陀螺仪和加速度传感器的帆船运动姿态测量方法[J].太赫科学与电子信息学报，2014，12(2)： 183- 189.

[4] 樊秀梅，单志广，张宝贤.容迟网络体系结构极其关键技术研究[J].电子学报，2008，36(1)： 161- 170.

[5] CERF V, BURLEIGH S C, HOOKE A,etal. RFC 4838： Delay- tolerant networking architecture[S]. IETF： 2007.4.

[6] ZHANG Y, BAI X Y. Congestion control mechanism in delay tolerant networks[C]∥Electronics Information and Emergency Communication(ICEIEC),2015 5th International Conference. Inner Mongolia, Huhhot： IEEE Press, 2015,112- 115.

[7] 张建华.无线传感器网络技术概述[J].消费电子，2013(2)： 3- 4.

[8] William Stallings著.高速网络与互联网——性能与服务质量[M].齐望东，薛卫娟，傅麒麟，等译.北京： 电子工业出版社，2003.

[9] 马新华，容晓峰.基于排队模型的无线传感器网络实时性能分析[J].西安邮电学院学报，2009，14(1)： 112- 115.

[10] 李宇光.基于Matlab的排队问题仿真[J].武汉理工大学学报，2010，32(6)： 892- 895，903.

Abstract： In this paper, we propose a design model based on Delay Tolerant Network(DTN) architecture to monitor multi- parameter in sailing, thus to handle the issue of multi- node joint operation. We also provide a simulation method based on the theory of queuing to analyze the performance of the system,which sacrificed the real- time ability in exchange for the reliability. We concluded that in resource- constrained environments (with 0.1 packet loss rate), delay- tolerant system can improve the utilization rate of the data by up to about 17.3%, which significantly improved the objectivity of the monitoring results. Through prototype equipment using in the real training course, we validate the feasibility and reliability of this design method.

Keywords： joint operation; delay- tolerant network; VMG; queuing theory

start(n)=max[over(n-1),arrive(n)].

wait(n)=3×start(n)-arrive1(n)-arrive2(n)-arrive3(n),

over(n)=start(n)+serve(n).

DesignofSailingVMGParameterMonitoringSystemBasedonDelay-TolerantNetworkModel

LIN Hanxiang, LI Lingling, REN Jiuchun, ZHU Qian

(DepartmentofCommunicationScienceEngineering,FudanUniversity,Shanghai200433,China)

TN914;TN92;TN99

A

0427- 7104(2017)01- 0079- 10

2016- 04- 21

上海市科研计划项目(14231202102)

林汉翔(1991—)，男，硕士研究生；任久春，讲师，通信联系人，E- mail： renjiuchun@fudan.edu.cn.