基于模糊滑模控制的异步电动机矢量调速系统的建模与仿真
2017-10-13李智鹃周凌辉李成阳
李智鹃,周凌辉,李成阳
基于模糊滑模控制的异步电动机矢量调速系统的建模与仿真
李智鹃1,周凌辉2,李成阳2
(1.中国船舶工业集团公司第708研究所,上海200011;2.武汉船用电力推进装置研究所,武汉430064)
本文根据模糊滑模控制和异步电机矢量控制方法,在Simulink仿真环境中建立了一种基于模糊滑模控制的异步电机矢量调速模型。该模型仿真结果说明,与传统的PID控制相比,基于模糊滑模控制的异步电机调速系统具有更好的动态性能和鲁棒性。
模糊滑模控制 PID控制 矢量控制 异步电动机调速系统
0 引言
异步电机是一个高阶、非线性、强耦合、多变量的控制系统。为了提高电机的动态性能,矢量控制策略被应用于异步电动机调速系统中。矢量控制的基本原理是基于派克变换(Park Transformation),将产生转矩的电流分量和产生磁链的电流分量解耦。通过矢量控制方法,异步电动机可以像简单的直流电动机一样分别对定子磁链和转子转矩独立控制。
但是矢量控制依赖电机参数的辨识精度。当由于异步电机调速系统本身的非线性和电机参数辨识不准确等因素,因此矢量控制的控制精度会受到较大的影响。并且由于PID控制的抗干扰和抗参数摄动的鲁棒性不够理想,因此往往不能获得理想的动态性能。模糊滑模控制(Fuzzy SlideModeControl,FSMC)结合了模糊控制对模型参数的不敏感特性和滑模控制结构简单、鲁棒性强的特点,在矢量控制系统中引入模糊滑模控制器将有效的提高系统的控制精度和鲁棒性。
本文在异步电机矢量调速系统的基础上,根据模糊滑模控制理论,设计了一种模糊滑模速度控制器。在Simulink环境下建立基于模糊滑模控制的异步电机矢量调速系统的仿真模型,通过与采用PID控制器的异步电机矢量调速系统比较在突增负载下系统的动态性能,验证模糊滑模控制在性能上的优越性。
1 模糊滑模控制和矢量控制原理
1.1 模糊滑模速度控制器的设计
滑模控制是变结构控制中最主流的控制方法。基本思想是利用不连续的控制规律,使系统的结构沿着状态空间一个特殊超平面不断变换,迫使系统状态沿着平面驱向平衡点滑动,最终稳定于平衡点及附近的某个允许领域内。


根据滑模变结构的存在条件

可以得知调速系统在任何一个状态空间点出发都能够达到滑模面,但不能获得到达的路径,因此需要趋近律定义系统到达滑模面的路径。通常滑模控制采用指数趋近律。指数趋近律如下式所示
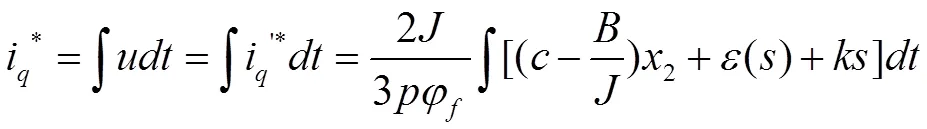
常规滑模控制在滑模面附近容易出现“抖动”现象。如上式所得的滑模控制律中参数和若采用常数,那么系统有可能出现较大的抖动,导致动态性能较差。因此可以引入鲁棒性较强的模糊控制方法使参数和随系统位置的变化而变化,从而提高系统的动态性能。
模糊控制由模糊化、知识库、模糊推理以及去模糊四个环节构成,首先需要将参考输入量变换到论域中,得到相应的模糊集合。若s,,和的模糊集合为:

可得如图1所示的隶属度函数。
图1 隶属度函数
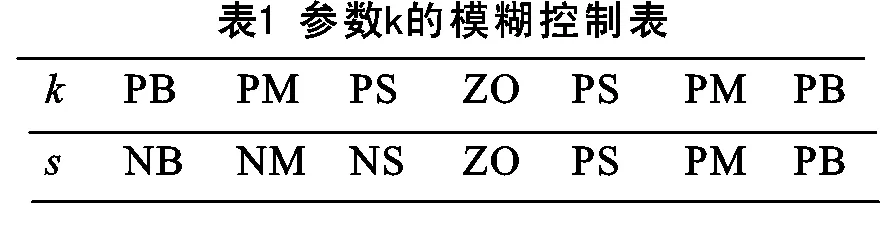
模糊推理采用Mamdani法,算法由Simulink模块内置。
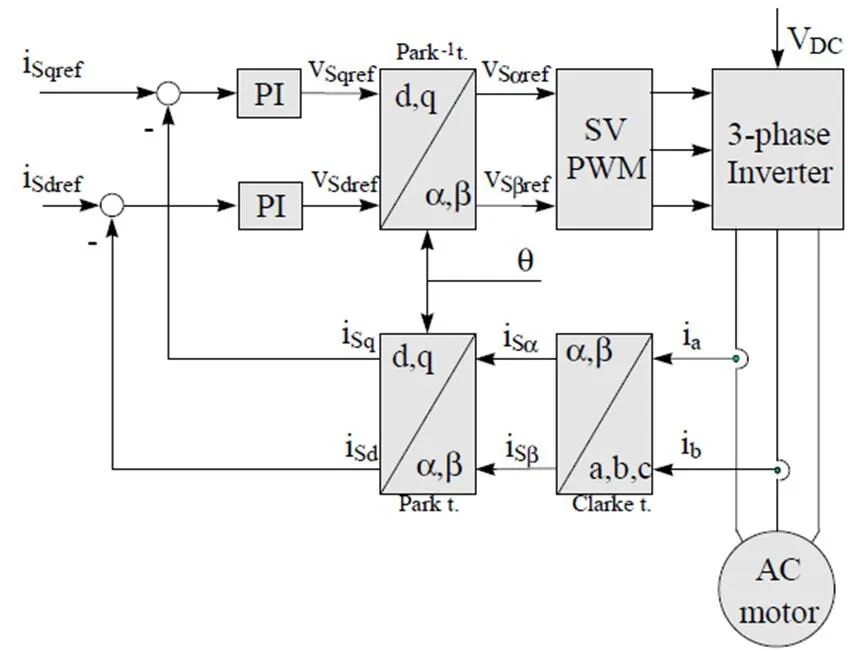
图2 矢量控制原理
1.2 矢量控制
矢量控制的基本思想是首先通过克拉克变换(Clerk Transformation),将三相的电流a,b,c转换两相静止坐标系α,β,然后通过派克变换将异步电机的定子电流矢量分解为d/q轴上的电流分量d和q。d和q分量分别控制电机的磁通链和转矩,从而实现电机磁通链和转矩的解耦,使异步电机具有类似于直流电机的控制性能。
矢量控制的基本原理如图1所示。
利用矢量变换可以获得异步电动机在MT轴系的电压方程:
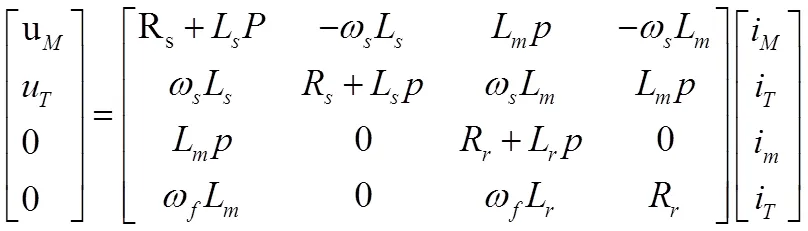
式中12位定子和转子的电阻,Lr为定子和转子绕组的自感,m为定转子绕组之间的互感在异步电动机的矢量控制中,定子电流分量m和定转子之间互感之间满足以下方程:
式中的2为转子的励磁时间常数。
电机的电磁转矩方程为:
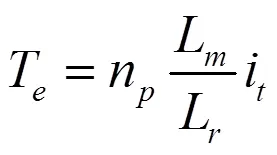
根据上述方程可知,当转子的磁链达到稳定时,电磁转矩只由电流分量t决定。
图3 矢量控制异步电机系统仿真模型
2 基于模糊滑模控制的异步电机矢量调速系统模型
在2013版MATLAB的Simulink仿真环境下,利用Simulink模块库中的模块搭建基于模糊滑模控制的异步电机矢量控制模型。模型主要包括矢量控制模块、异步电机模块、IGBT逆变器模块、直流电源模块。矢量控制模型的结构如图3所示。
2.1 模糊滑模速度调节器
根据2.1节中模糊滑模控制原理,基于模糊滑模控制的速度调节器结构如图4所示。

图4 模糊滑模速度调节器
2.2 矢量控制模块
矢量控制模块的结构如图3所示。

图5 矢量控制模块
模糊滑模速度调节器(FSMCSpeedController)的输出信号是根据给定的转速差,计算模块中计算q轴电流指令q。dq到ABC转换模块(dq to ABC Conversion)负责完成d和q到a,b,c电流指令的变换。电流调节器模块(CurrentRegulator)采用滞环控制的方法,使实际的电流值跟随给定电流指令的变化。角度计算模块(Teta Calculation)的作用是计算d轴的相对于静止坐标系的夹角。ABC到dq的转换模块(ABC to dq Conversion)的作用是根据角计算dq轴的分量d和q。d计算模块(dcalcuation)的作用是根据转子磁链和转子实际磁链计算定子电流的励磁分量d。
3 模型动态性能仿真和结果分析
利用上述矢量控制异步电机模型进行电机动态性能的仿真研究。仿真过程中利用示波器模块对定子线电压、定子三相电流、转子转矩和电机转速进行测量。
三相异步电机的参数如下表所示:

作为对比的PID速度调节器参数如下:积分增益i=26,比例增益p=13;电流调节器的滞环宽度为20 A。
模型仿真参数采用离散计算方式,采样时间为s=2e-6,仿真时长为5 s,参考转速为120 rpm。在2 s时加入负载转矩200NM。
采用模糊滑模控制速度控制的异步电机矢量调速系统的定子线电压、定子三相电流、转子转矩、电机转速的响应波形如图6所示。
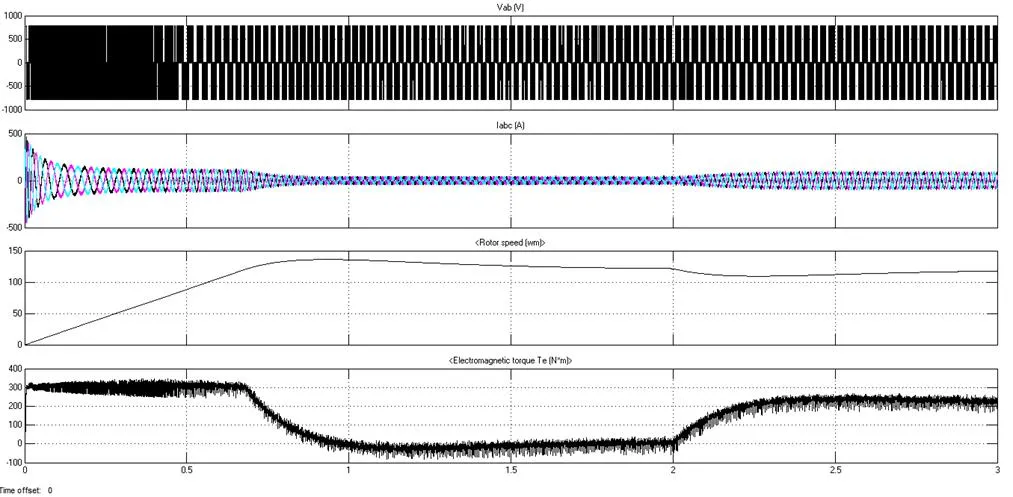
图6 基于模糊滑模控制的系统响应
采用传统PID速度控制的异步电机矢量调速系统的定子线电压、定子三相电流、转子转矩、电机转速的响应波形如图7所示。

图7 基于PID控制的系统响应
从仿真结果可以看出,采用模糊滑模控制的异步电机矢量调速系统响应时间更快,转速和转矩几乎没有超调量,对外界的扰动具有良好的鲁棒性。
4 结论
本文建立基于模糊滑模控制的异步电机矢量调速系统的Simulink模型,通过与采用传统PID速度控制的异步电机矢量调速系统进行仿真比较,验证了模糊滑模控制对提高异步电机在负载突增突减的变化过程中动态响应和鲁棒性的作用。该模型有助于未来进一步研究异步电机的模糊控制和滑模控制等先进控制方法。
[1] 马志源.电力拖动控制系统[M].科学出版社.
[2] 李明,朱美强,马勇.MATLAB/SIMULINK通用异步电机模型的分析与应用[J].工矿自动化,2005.
[3] 王海峰,任章.基于MATLAB/SIMULINK的异步电动机建模与仿真[J].电机控制学报,2000.
[4] 高为炳.变结构控制的理论与方法[M].北京:科学出版社.
[5] 刘金琨.滑模变结构控制MATLAB仿真[M].清华大学出版社.
Modeling and Simulation of Induction Motor Speed Control System Based on FSMC and Vector Control
Li Zhijuan1, Zhou Linghui2, Li Chengyang2
(1.The 708th Institute,Shanghai 200011,China; 2. Wuhan Institute of Marine Electric Propulsion,Wuhan 430064, China)
TM46
A
1003-4862(2017)03-0036-04
2017-01-15
李智鹃(1984-),女,工程师。研究方向:船舶电气。
