爆破荷载下巷道关键块体区间的非概率可靠性

高赛红，曹 平，汪胜莲，陈 瑜



爆破荷载下巷道关键块体区间的非概率可靠性

高赛红1, 2，曹 平1，汪胜莲2，陈 瑜1

(1. 中南大学资源与安全工程学院，长沙410083；2. 江西理工大学应用科学学院，赣州341000)

在关键块体稳定性的研究过程中，传统方法需要通过力学试验获得岩体力学参数，然而由于岩体结构复杂，力学试验样本数量有限，很难确定某一个力学参数的概率密度分布，严重影响传统随机概率可靠性分析方法的准确性。当采用区间非概率可靠性分析方法计算可靠度时，通常采用区间数来表示参数的取值，能够较好地反映样本数据较少时参数取值的不确定性，确定某一参数的取值范围比确定参数的概率分布容易。根据区间数学理论，采用区间数表示参数取值，在分析参数取值特性基础上，采用岩体区间强度值，以此反映围岩可靠性分析的不确定性特征。通过探讨区间非概率可靠性指标求解方法，建立爆破荷载下区间可靠性综合分析模型。将提出的方法应用到具体工程中。结果表明：区间非概率可靠性分析与安全系数区间范围和随机可靠度相比，具有无需求解概率密度函数，通过较少样本的区间表示即可实现可靠性分析，能够表征关键块体整体稳定可靠特征的优点。

爆破荷载；损伤；巷道；关键块体；区间非概率可靠性

在采矿开挖工程中，由于岩体被节理等结构面切割成大小不同、形状不一的各种岩块，其中暴露在临空面上的某些块体在失去原有的静力平衡状态后，会沿着结构面滑移并导致局部掉块，进而产生连锁反应，造成一定范围内岩体的局部失稳，因此块体稳定性是研究地下工程围岩整体稳定性的一项极为重要的内容。由GOODMAN[1]和石根华[2]提出的块体理论是近年来发展和完善起来的一种适合于工程岩体稳定性分析的有效方法。

目前，考虑围岩稳定可靠性分析方法研究取得了卓有成效的成果，如基于概率理论的可靠性分析方法逐渐被应用于岩土工程稳定可靠性分析[3−4]，为考虑不确定性因素影响的岩土工程计算提供了一种行之有效的方法。

尽管基于概率理论的可靠性分析方法在围岩稳定性研究中取得了不同程度的进展，但仍然存在诸多不足。其一，围岩稳定性概率可靠性分析均需确定参数概率分布形式，这在勘察取样点及试验数据有限的情况下是困难的，且概率分布形式的假定存在适用性的问题，不同形式所对应的可靠性指标存在较大差异 性[4−5]。其二，概率可靠性分析模型对参数取值的敏感性很强，分布函数截尾数据的小误差能导致不可接受的可靠性指标分析结果，这在数据量有限时往往难以避免[5]。其三，围岩是否稳定，是相对性，没有严格的区分指标，存在模糊性。因此，有必要针对上述存在的问题展开进一步研究，建立在数据量较少的情况下，也能有效地分析围岩体可靠性的分析方法。

基于区间理论的非概率可靠性分析方法[5−6]为本文作者研究提供了一个良好的思路，区间数能够较好地反映样本数据较少时参数取值的不确定性，减少了对数据信息量的过多依赖。在工程研究中，某个力学参数范围的确定往往比确定单一的具体定值或参数的概率分布要容易得多，因此，采用区间非概率可靠性分析方法对地下巷道节理岩体稳定性进行评价成为本文研究的重点。

另一方面，因开挖和爆破作业，特别是频繁爆破作业，会在一定程度上造成岩体损伤，从而导致岩体完整性降低和力学参数弱化。爆破开挖损伤区，亦称爆破开挖扰动区，此区域内的岩体，由于卸载交替作用和爆破动应力产生的累积损伤效应，岩体逐渐从未扰动状态向完全扰动状态过渡。爆破规模较大或距离爆源较近的岩体，爆破损伤较严重，受扰动程度也较大，甚至产生断裂或破碎，反之，则爆破损伤较轻，受扰动程度也较小，甚至不会受到爆破开挖的影响。因此，岩体爆破开挖损伤程度，以及受扰动程度与岩体开挖方法，爆破作业规模、爆心距以及岩体质量、岩体结构种类等因素密切相关。岩体爆破开挖损伤程度和受扰动程度不同，则岩体完整性降低程度和岩体力学参数的弱化程度也不同。Hoek-Brown经验公式只考虑了未扰动和扰动岩体两个极端情况，而不考虑岩体实际受扰动程度对岩体力学参数弱化程度的影响，必然导致计算结果产生较大偏差。开挖方法影响系数f，考虑了不同开挖方法对岩体扰动程度的影响，对b和的取值方法进一步完善，然而给出的开挖方法影响系数f难以确定，不便于工程应用。在确定b和的取值时，对介于未扰动状态和完全扰动状态之间的岩体，若按未扰动岩体处理，会导致岩体力学参数取值偏高；若按照完全扰动岩体处理，又会导致岩体力学参数取值偏低。因此，如何有效地、简便地确定开挖和爆破带来的影响，真实地反映岩体受扰动程度，以便能够更好地确定介于未扰动状态和完全扰动状态之间岩体的力学参数，已成为Hoek-Brown经验公式计算岩体力学参数的关键问题之一。由于岩体受扰动程度与爆破损伤程度、岩体完整性系数密切相关，为克服Hoek-Brown经验准则及其上述改进公式的不足，更好地描述岩体受扰动程度对岩体力学参数的影响，准确地表征不同扰动程度状态下参数b和的取值，考虑爆破损伤作用时Hoek-Brown法值取值根据区域爆破损伤参数确定，即已有岩体损伤量的表征为单个测量点，或者单个测量剖面岩体的损伤提供有效途径。但在实际工程中，人们主要关注的是区域岩体的损伤情况，单个剖面或者单个点的结果无法表征或者代表区域岩体的损伤情况。为此，本文作者提出基于正态分布和指数正态分布方法确定区域岩体损伤的指标。

综上所述，本文作者根据区间数学理论[7]，采用区间数表示参数取值，在分析参数取值特性基础上，采用岩体区间强度值[8−9]，以此反映围岩可靠性分析的不确定性特征。在充分考虑爆破损伤的情况下，通过探讨区间非概率可靠性指标求解方法，建立爆破荷载下地下巷道围岩可靠性综合分析方法，并与随机可靠度的计算结果进行比较，以期进一步完善岩体稳定可靠性的分析方法与理论。

1 爆破荷载下关键块体区间非概率可靠性模型

1.1 爆破荷载下关键块体区间非概率可靠性分析的功能函数

块体沿单结构面滑动和沿双结构面滑动的稳定可靠性分析极限状态方程可表示为

为了便于分析，根据区间值标准化方法先将区间功能函数式转化为标准形式，即

1.2 区间非概率可靠性求解方法

由非概率可靠性理论可知标准化区间功能函数式(3)与(4)的非概率可靠性指标(1，2)的求解式[6]为

并满足条件：

1) 先讨论以弯沉表达的极限方程情况下区间非概率可靠性的求解问题，列出扩展空间的原点和形成的对称凸域的顶点(=1, 22)的22−1条超射线，记为，并满足；

3) 舍去复数解，并取实数解的绝对值，最小的即为结构区间非概率可靠性指标。

同理，应力表达的极限方程(5)的求解问题同1)、2)和3)，求得非概率可靠性指标解集合，进而由式(6)可得结构区间非概率可靠性指标。

1.3 关键块体滑动力学模型中爆破荷载的确定

爆破地震惯性力计算如何确定呢？块体动力稳定性分析是将分布在块体上的动态爆破惯性力拟静力化，然后作为一种荷载作用参与块体稳定性计算。这种方法分析简便，概念清晰，避开爆破地震特有的复杂性，且能较好地结合工程现场实测资料，具体计算公式如下：

目前，国内一致认为块体等整体性构筑物的破坏与质点震动速度关系较为密切，而且采用质点震动速度可将地震波所携带的能量与所产生的动应力相联系起来。同时质点震动速度测试又较为简便，所以质点震速已成为衡量爆破地震效应的最常用指标[12−14]。

对于简谐振动，速度与加速度峰值间存在下面的关系：

借助于这一基本关系，可将同样的关系推广到爆破振动的统计规律中来，而此时的不再是某一确定简谐振动的频率，而应该是具有确定统计意义、有代表性的频率值[15−17]。由于地震波是多频率成分组成的复杂震动，且各频率成分的贡献各有大小[18−20]，如果选取贡献最大的频率作为，文献[15]显示其结果是安全的。因此，采用文献[14]方法，将爆破振动信号进行小波包分析，即可得爆破震动信号在不同频带上的能量分布图以及各频带上的主频，并将其中贡献最大的主频率作为。

1.4 考虑爆破损伤作用时Hoek-Brown法值取值

首先测量研究区域内的未损伤的若干剖面波速值V，再测量爆破损伤后的波速值DV，对波速值V正态分布进行正态分布拟合，求解V的正态分布与指数正态分布的概率密度函数，求出V在正态分布中概率密度最大值对应的V，记作NV，求出V在指数正态分布中概率密度最大值对应的V，记作EV；同理求出爆破损伤后DV对应的NDV，EDV则该区域基于正态分布和指数正态分布的损伤量的和分别可以表示为

区域损伤的95%参考值范围亦可以通过以上求得概率密度函数得到，计算思路同上。取95%参考值范围下限可求得区域损伤95%参考值范围的下限，取95%参考值范围上限可求得区域损伤95%参考值范围的上限。

2 工程应用与讨论

2.1 工程概况

一露天和地下联合开采矿山，有6种力学介质，即矽卡岩、硅化岩、次英安斑岩、硫铁矿体、褐铁矿、花岗闪长斑岩。根据岩体结构特征、岩体分级指标和工程经验，综合选取的岩体力学参数。

分析区域采场顶板为硅化岩岩组，该岩组为近矿体围岩蚀变形成，为块状结构，主要发育5组节理，其产状分别为：332°∠65°、53°∠52°、26°∠85°、179°∠72°、213°∠50°，节理长度大于1.5 m，同一地点大约3组节理，局部填充有少量方解石、铁质和泥质，节理面平直，裂隙水微弱，开挖面产状260°∠15°。本研究中选取巷道断面为三心拱，其净宽为4.2 m，墙高为3.0 m，拱高度为1.4 m。

主要力学参数如下：弹性模量6130~6256 MPa；泊松比0.12~0.15；密度2736~2849 kg/m3；抗拉强度0.85~1.03 MPa。

采用Hoek-Brown法确定爆破扰动下粘结力和内摩擦角，计算中的取值根据1.4节区域损伤的方法求解，求得粘结力为1.12~1.91 MPa；内摩擦角为28°~36°。

该矿山巷道由于结构面的切割，在巷道周围形成了大量的块体。矿山爆破与开挖等作业过程经常会对这些块体造成扰动，不但对矿山生产是一个巨大隐患，而且对人员的安全也构成了巨大的威胁。为了保证安全生产，需要对巷道周围的块体进行稳定性分析。拟通过块体分析软件进行分析，得到块体相关数据，然后计算其区间非概率可靠度和随机可靠度，并进行比较分析。

2.2 结果与讨论

根据第1节的理论计算方法，各结构面的赤平投影见图1。本研究中每次参与组合的结构面最多为3条，由于该巷道受5条结构面切割，故共需进行10次分析。任选一组结构面，切换到3D块体预览界面即可从不同角度分析由该组结构面切割所形成的块体，见图2。

进行地应力分析时，在地应力可视化界面可以看到块体的每一个面上不同位置处的应力，有正应力和切应力两种视图，不同的颜色代表不同大小的应力。图3和4所示分别为正应力视图和切应力视图。从图3和4可以看出，由该组结构面切割形成的块体各面上的正应力大部分集中在0~2.0 MPa之间，其中，最小正应力为0.067 MPa，最大正应力为1.875 MPa；切应力大部分集中在0~0.8 MPa之间，最小切应力为0.06 MPa，最大切应力为0. 873 MPa。

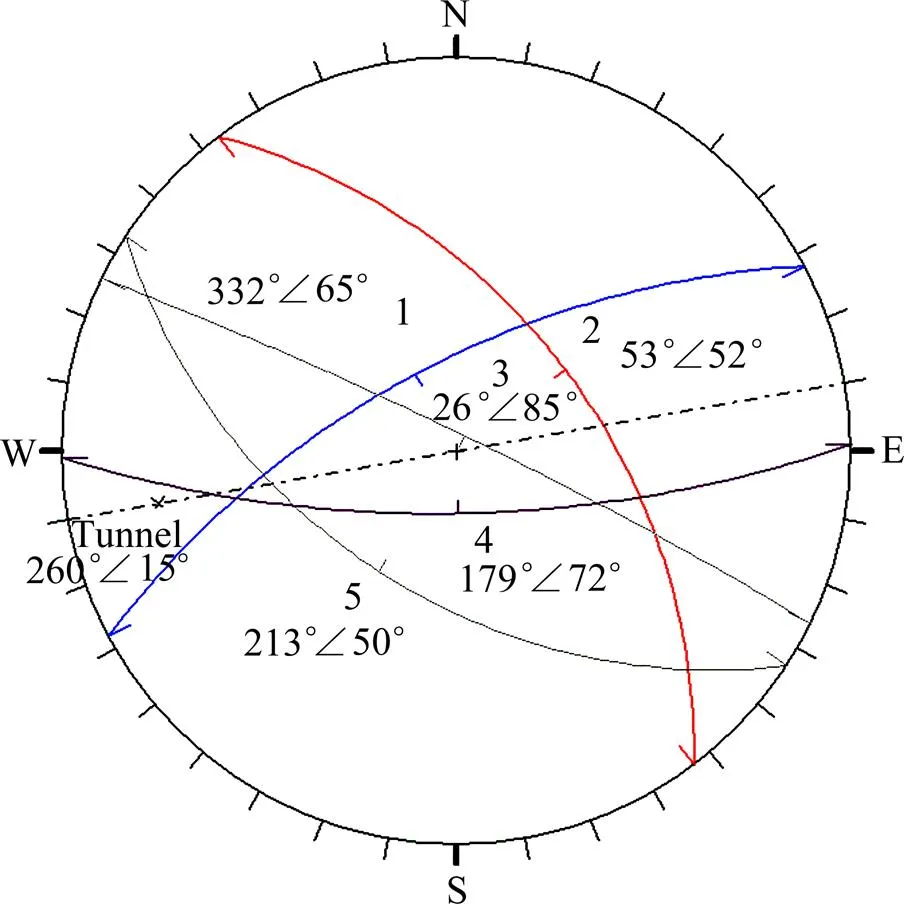
图1 各结构面的赤平投影图

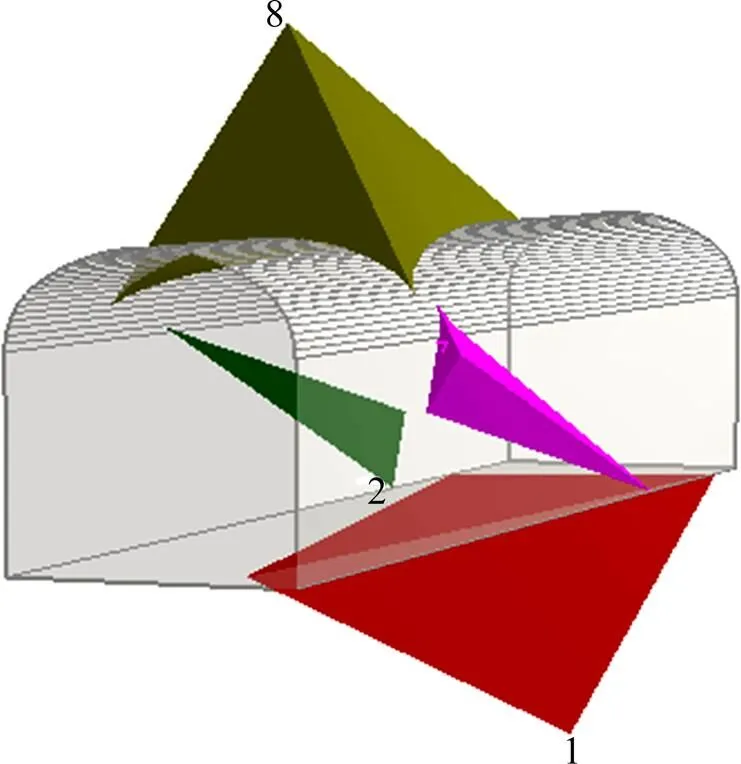
图2 3D块体透视图

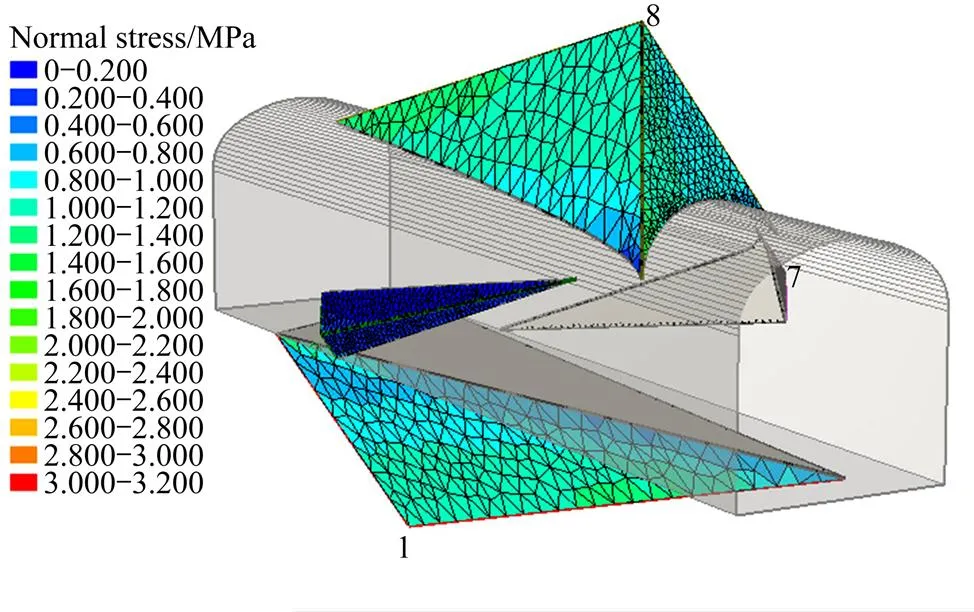
图3 3D正应力透视图

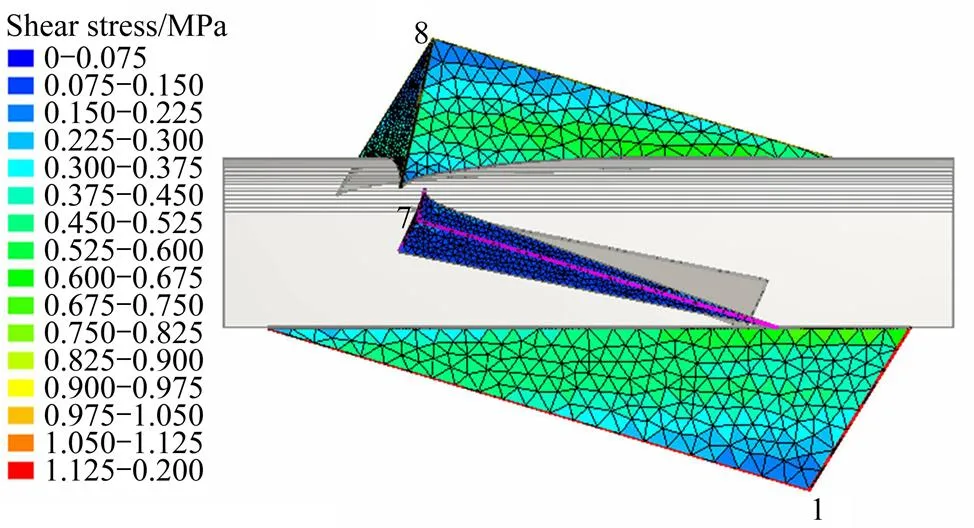
图4 3D切应力侧视图

为分析计算结果，可以通过3D视图或等高线图表征在不同的倾向与倾角时形成的块体的各种特征，如所需支持力、最大块体体积、最大块体质量以及最小安全系数等。图5~7所示分别为不同的倾向与倾角时块体所需支持、不同的倾向与倾角时的最大块体体积、不同的倾向与倾角时的最大顶高度3D视图；图8~10所示分别为不同倾向与倾角时所需支持力、不同倾向与倾角时最大块体质量、不同倾向与倾角时块体最大顶高度等高线图。从图中可以发现，在选定的结构面组合中，当巷道选取不同的倾向和倾角时，所需的支持力的大小、切割形成块体的最大体积和最大可见高度等是不同的。当倾向为90°，倾角为0°时，所需支持力的大小最大，为0.061 MPa；当倾向为270°、倾角为50°时，切割形成的块体体积最大，为43.291 m³，此时的块体质量也是最大的；当岩体允许暴露面积为43.40 m2，倾向为258°，倾角为53°时，巷道能够承受的高度最大，为4.36 m。可见，当倾角或倾向逐渐变化时，选定的结构面组合切割形成的块体的所需支持力、最大质量、最大顶高度以及最小安全系数都是不同的。

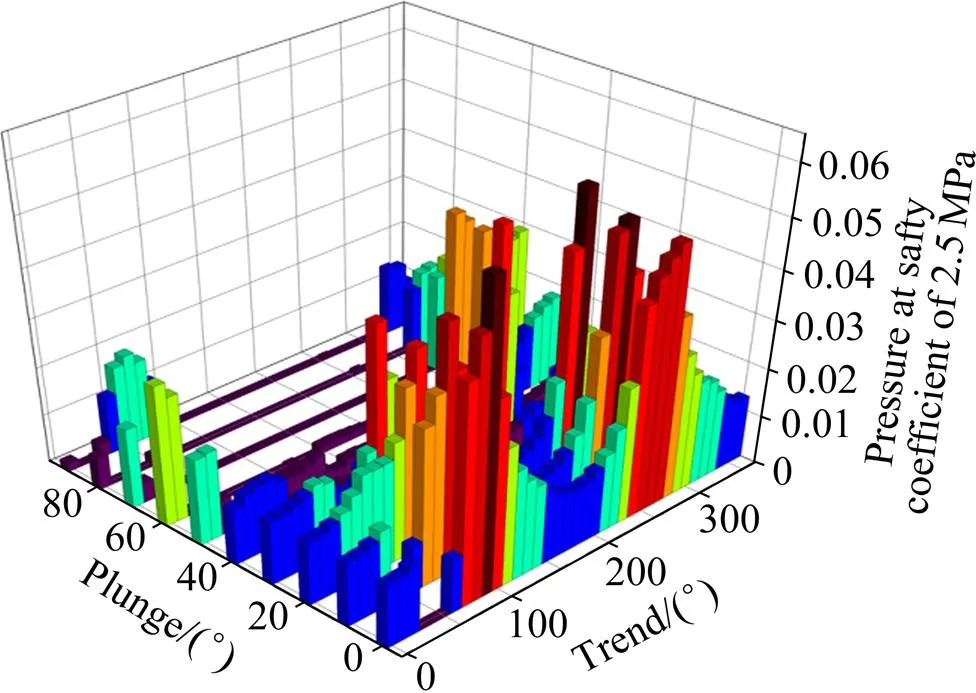
图5 不同的倾向与倾角时块体所需支持3D视图

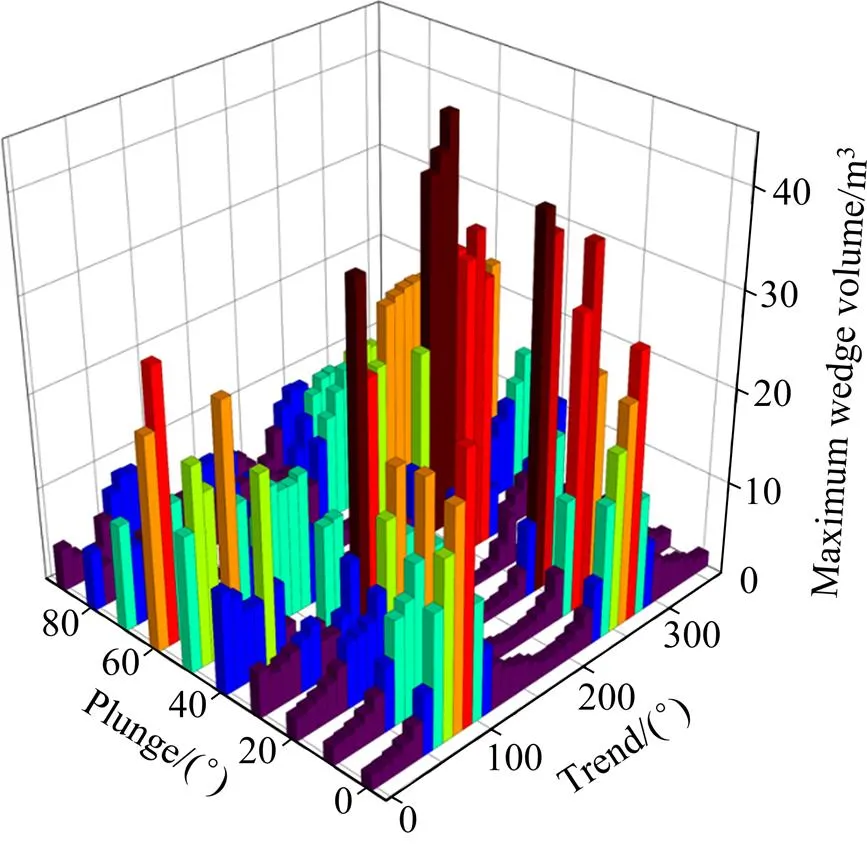
图6 不同的倾向与倾角时的最大块体体积3D视图

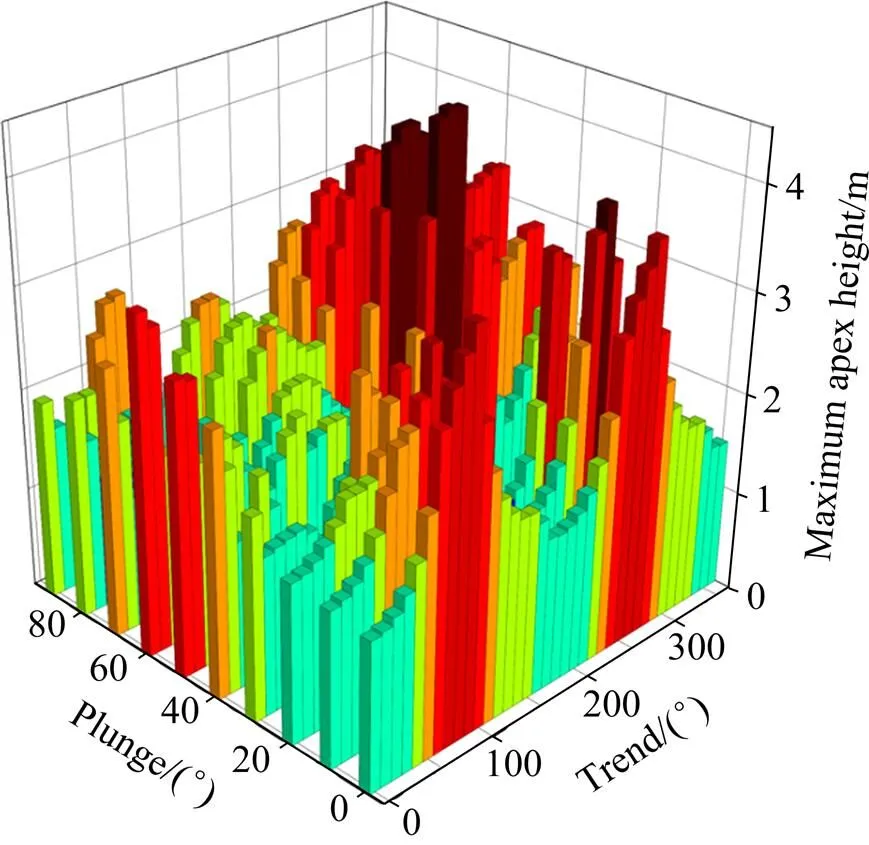
图7 不同的倾向与倾角时的最大顶高度3D视图

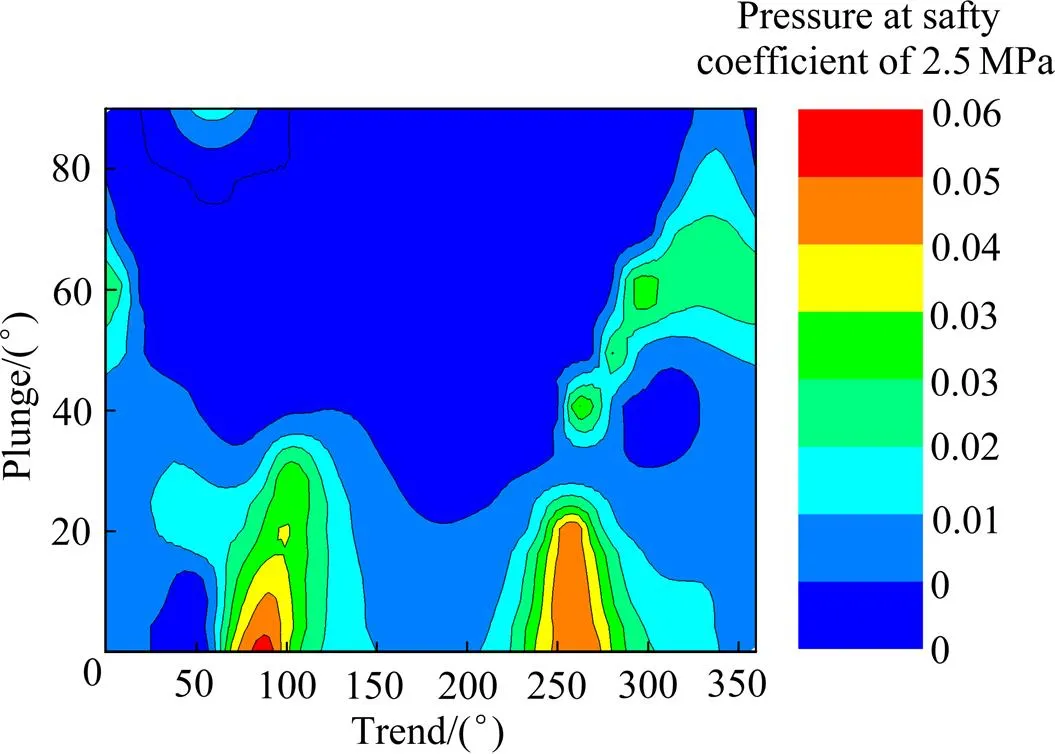
图8 不同倾向与倾角时所需支持力等高线图

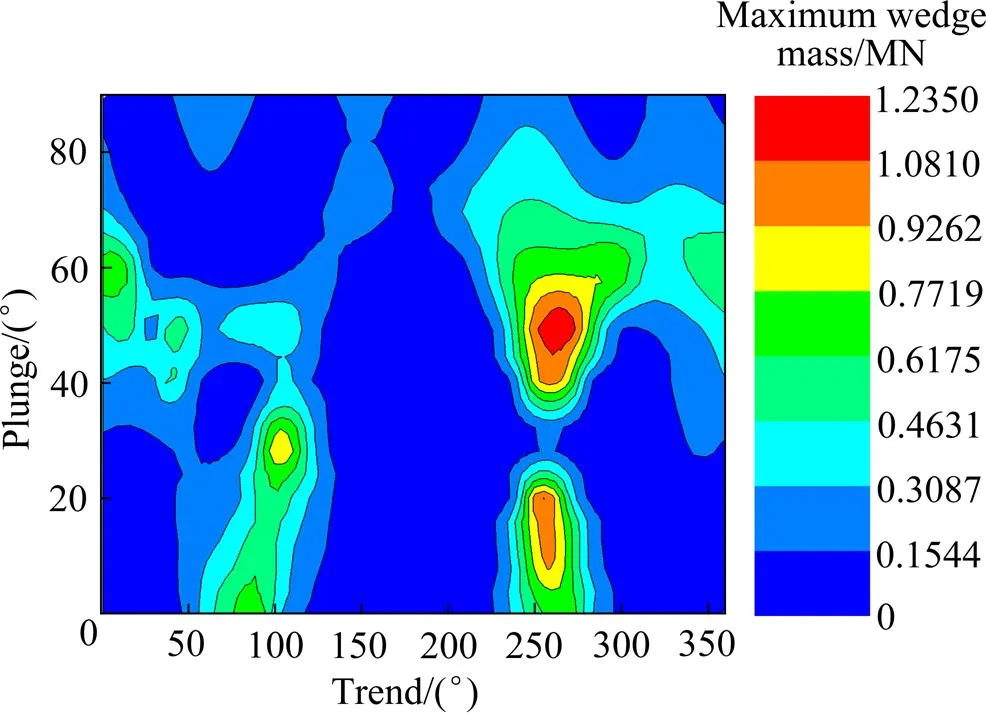
图9 不同倾向与倾角时最大块体质量等高线图

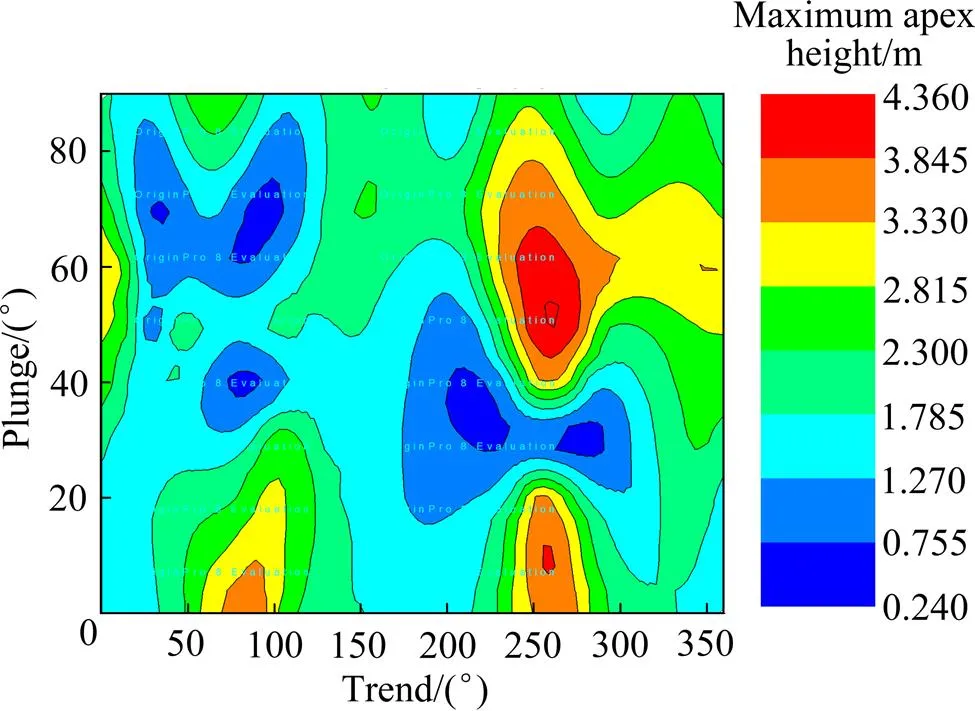
图10 不同倾向与倾角时块体最大顶高度等高线图

不同的结构面组合所形成块体的相关参数，包括块体编号、安全系数、块体体积、块体质量、滑动结构面、滑动面面积、滑动面正应力和滑动方向，将结果分别记录在表1中。

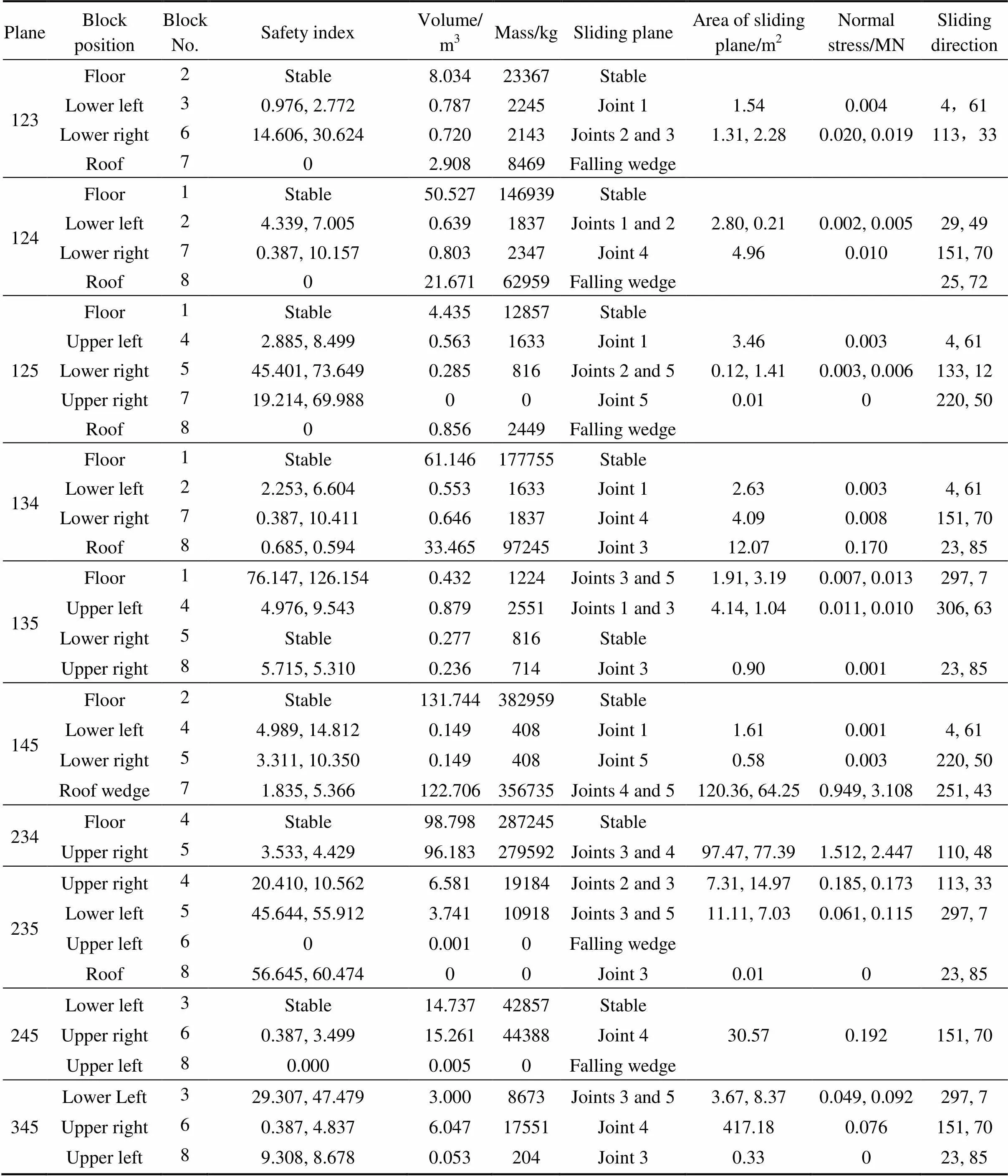
表1 不同结构面形成块体的相关参数

通过调查统计，得到5组结构面的抗剪强度区间参数，结果见表2。

根据本文方法进行区间可靠度计算，将其计算结果列在表3中，另外，表3也列出了安全系数、随机可靠度计算结果。值得说明的是，结构面123所形成的块体中，块体2在巷道底部，为稳定块体，无需进行可靠度计算；块体3沿结构面1滑动；块体6沿结构面2和3滑动；块体7为直接垮落块体。

表2 结构面抗剪强度参数

表3 不同块体的区间可靠度和随机可靠度

由表3中数据可以看出，结构面1参与构成的可动块体共有19个，结构面2参与构成的块体共有17个，结构面3参与构成的块体共有17个，结构面4参与构成的块体共有16个，结构面5参与构成的块体共有19个，且结构面1和结构面2参与构成的块体中，直接垮落块体和不稳定块体最多，因此要考虑重点监测由结构面1和结构面2构成的块体，采取适当的支护方式以保证施工过程中的安全。

在工程问题的研究过程中，由于调查数据是有限的，因此很难确定某一个参数准确的概率分布，而采用区间可靠度分析方法计算可靠度时，通常用区间数来表示参数的取值，能够较好地反映样本数据较少时参数取值的不确定性，确定某一参数的取值范围也比确定参数的概率分布容易。随机可靠度在计算中，先根据调查数据以及经验公式假设了参数的概率分布，但是不能确定假定的概率分布是否满足适用条件。同时，由于随机可靠度分析模型对于参数取值的敏感性很强，采用不同形式的概率分布进行计算时，得到的可靠度指标也存在较大差异。对比分析表3中计算所得的结果，块体1348、块体2456和块体3456的区间可靠度与随机可靠度差别较大，究其原因是随机可靠度计算中参数的概率分布的适用性存在问题，而采用区间可靠度得到的结果与实际情况一致。块体1247和块体1347采用两种方法计算得到的可靠度指标均小于1，为不可靠块体，应当采取适当的支护方式进行支护。其余块体采用这两种方法计算得到的可靠度均大于1，认为是可靠的。通过比较区间安全系数、随机可靠度及区间可靠性的计算结果可以发现，安全系数分析只能实现特定参数的单一稳定性评估，安全系数的区间为两个极端情况，很难在工程中应用，且不能系统性对关键块体进行评估；随机可靠度的计算结果变化幅度较大，概率密度函数较难确定，数据需求量大，工程应用存在一定困难；区间概率可靠度分析时无需求解概率密度函数，通过较少样本的区间表示即可实现可靠性分析，能够表征关键块体整体的稳定可靠特征。

但是，地下工程中块体的滑落并不是一次性完成的，而是逐渐发生变化的一个动态的过程，因此不能因为某次计算结果是稳定的，就完全肯定某块体是可靠的而不予重视，在后续爆破作业等的影响下，会导致某些结构面或裂隙的加剧，最终使原本稳定的块体发展成为不稳定的块体。因此，为了保证作业过程中人员及设备的安全，需要对所有有运动倾向的块体进行监测，及时采取措施，并进行合理的支护。

3 结论

1) 在关键块体稳定性的研究过程中，由于调查数据是有限的，因此很难确定某一个参数准确的概率分布，而采用区间可靠度分析方法计算可靠度时，通常用区间数来表示参数的取值，能够较好的反映样本数据较少时参数取值的不确定性，确定某一参数的取值范围也比确定参数的概率分布容易。

2) 根据区间数学理论，采用区间数表示参数取值，在分析参数取值特性基础上，采用岩体区间强度值，以此反映围岩可靠性分析的不确定性特征，通过探讨区间非概率可靠性指标求解方法，建立了爆破荷载下区间可靠性综合分析模型。

3) 将提出的方法应用到具体工程中，并同时计算了区间安全系数、随机可靠度，结果显示，安全系数分析只能实现特定参数的单一稳定性评估，不能系统地对关键块体进行评估；随机可靠度的计算结果变化幅度较大，概率密度函数较难确定，数据需求量大，工程应用存在一定困难；而区间概率可靠度分析时无需求解概率密度函数，通过较少样本的区间表示即可实现可靠性分析，能够表征关键块体整体的稳定可靠特征。

[1] GOODMAN R E. SHI G H. Block theory and its application torock engineering[M]. Englewood Cliffs: Prentice-Hall, 1985.

[2] 石根华. 岩体稳定分析的几何方法[J]. 中国科学, 1981, 4: 487−495. SHI Gen-hua. Geometrical approach of rock mass stabilization in rock mass stability analysis[J]. Science in China, 1981, 4: 487−495.

[3] 阚卫明, 孙万禾, 闫澍旺. 根据土的抗剪强度指标变异性和安全域检验地基承载力的可靠性[J]. 土木工程学报, 2001, 34(2): 101−104. KAN Wei-ming, SUN Wan-he, YAN Shu-wang. Reliability analysis for bearing capacity of foundation based on variation of shear strength and safety zone[J]. China Civil Engineering Journal, 2001, 34(2): 101−104.

[4] POPESCU R, DEODATISB G, NOBAHARC A. Effects of random heterogeneity of soil properties on bearing capacity[J]. Probabilistic Engineering Mechanics, 2005, 20(6): 324−341.

[5] 郭书祥, 吕震宙, 冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报, 2001, 18(1): 56−60. GUO Shu-xiang, LÜ Zhen-zhou, FENG Yuan-sheng. A non-probabilistic model of structural reliability based on interval analysis[J]. Journal of Computational Mechanics, 2001, 18(1): 56−60.

[6] 江 涛, 陈建军, 姜培刚, 拓耀飞. 区间模型非概率可靠性指标的一维优化算法[J]. 工程力学, 2007, 24(7): 23−27. JIANG Tao, CHEN Jian-jun, JIANG Pei-gang, TUO Yao-fei. A one-dimensional optimization algorithm for non-probabilistic reliability index[J]. Engineering Mechanics, 2007, 24(7): 23−27.

[7] ALEFELD G, MAYER G. Interval analysis: Theory and applications[J]. Journal of Computational and Applied Mathematics, 2000, 121: 421−464.

[8] 董陇军, 李夕兵. 地下硐室节理岩体区间非概率可靠性分析方法及应用[J]. 岩土工程学报，2011(7): 1007−1013. DONG Long-jun, LI Xi-bing. Interval non-probabilistic reliability method for surrounding jointed rock mass stability of underground caverns[J]. Chinese Journal of Geotechnical Engineering, 2011(7): 1007−1013.

[9] 董陇军, 李夕兵. 岩石试验抗压、抗拉区间强度及代表值可信度研究[J]. 岩土工程学报, 2010, 32(12): 1969−1974. DONG Long-jun, LI Xi-bing. Study of interval parameters and credibility of representative value of rock tensile and compression strength tests[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(12): 1969−1974.

[10] 张子新, 孙 钧. 块体理论赤平解析法及其在硐室稳定分析中的应用[J]. 岩石力学与工程学报, 2002, 21(12): 1756−1760. ZHANG Zi-xin, SUN Jun. Stereo-analytic method for block theory and its application in stability analysis of a cave[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(12): 1756−1760.

[11] GOODMAN R E. SHI G H. Block theory and its application torock engineering[M]. Englewood Cliffs: Prentice-Hall, 1985.

[12] PARIDA A, MISHRA M K. Blast vibration analysis by difference predict approaches-A comparison[J]. Procedia Earth and Planetary Science, 2015, 11: 337−345.

[13] A′LVAREZ-VIGIL A E, GONZA ´LEZ-NICIEZA C, GAYARRE F L, A′LVAREZ-FERNA′NDEZ M I. Predicting blasting propagation velocity and vibration frequency using artificial neural networks[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 55: 108−116.

[14] DONG Long-jun, WESSELOO Johan, POTVIN Yves, LI Xi-bing. Discriminant models of blasts and seismic events in mine seismology[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 86: 282−291.

[15] KHANDELWAL M，SINGH T N. Prediction of blast-induced ground vibration using artificial neural network[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(7): 1214−1222.

[16] ZHANG Ke, CAO Ping, LIU Zi-yao, HU Hui-hua, GONG Dao-ping. Simulation analysis on three-dimensional slope failure under different conditions[J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 2490−2502.

[17] YILDIRIM E, GÜLBAĞ A, HORASANG, DOĞAN E. Discrimination of quarry blasts and earthquakes in the vicinity of Istanbul using soft computing techniques[J]. Comput Geosci, 2011, 37: 1209−1217.

[18] KUYUK H, YILDIRIM E, DOGAN E, HORASAN G. An unsupervised learning algorithm: application to the discrimination of seismic events and quarry blasts in the vicinity of Istanbul[J]. Nat Hazards Earth Syst Sci, 2011, 11: 93−100.

[19] ZHAO Guo-yan, MA Ju, DONG Long-jun, LI Xi-bing, CHEN Guang-hui, ZHANG Chu-xuan. Classification of mine blasts and microseismic events using starting-up features in seismograms[J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 3410−3420.

[20] GARCIA B F, ALEJANO L, GONZA´LEZ-CAO J. Predicting the extent of blast-induced damage in rock masses[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 56: 44−53.

Non-probability reliability of key blocks of roadways subjected to blasting loads applying interval theory

GAO Sai-hong1,2, CAO Ping1, WANG Sheng-lian2, CHEN Yu1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. School of Applied Science, Jiangxi University of Science and Technology, Ganzhou 341000, China)

The mechanical parameters of rock obtained from laboratory tests are vital important to the stability investigations on key blocks. However, due to the restraints from the complicated rock structure and the limitation of available test data, it is difficult to determine the accurate probabilistic distribution of any mechanical parameter. Therefore, problems might be encountered in the traditional reliability analysis characterized by random probability. In the reliability indication process characterized by non-probabilistic reliability with interval theory, parameters are represented by the intervals which reflect the uncertainty caused by the limited sample data. In addition, it is easier to determine the value range rather than the probabilistic distribution of specific parameters. Based on the interval mathematical theory and the related analysis of parameter properties, the uncertainty of the reliability analysis of surrounding rock was indicated by the interval values of rock strength. The comprehensive analytical model was established by probing the computing method for the index of interval non-probability. Moreover, the interval value of safety index and the random reliability are obtained by applying proposed method in a specific engineering scenario. The following results were concluded, safety analysis index can only be used in the single stability evaluation of a specific parameter. While systematic evaluation of key blocks can not be conducted by applying safety index analysis. The engineering application of the random probabilistic method is restrained by the obtained result varying in a large range. The difficulties encountered in the indication process of probabilistic density function and the great data volume are needed, the determination of the probabilistic density function is not required when applying non-linear reliability analysis based on interval theory and, thus, the reliability analysis can be conducted based on interval presentation of limited sample data. The entire reliability characteristics of key blocks stability can be represented accordingly.

blasting loads; damage; tunnels; key block; non-probabilistic reliability analysis applying interval theory

(编辑 龙怀中)

Project(51274249) supported by the Natural Science Foundation of China

2016-05-30; Accepted date:2016-12-25

CAO Ping; Tel: +86-13973128263; E-mail: pcao_csu@sina.com

1004-0609(2017)-02-0325-10

TU457

A

国家自然科学基金面上项目(51274249)

2016-05-30；

2016-12-25

曹 平，教授，博士；电话：13973128263；E-mail: pcao_csu@sina.com