基于Heusler合金的自旋零能隙半导体

徐桂舟，徐 锋，王文洪

(1.南京理工大学,江苏 南京 210094)(2.中国科学院物理研究所 北京凝聚态物理国家实验室, 北京 100190)

基于Heusler合金的自旋零能隙半导体

徐桂舟1，徐 锋1，王文洪2

(1.南京理工大学,江苏 南京 210094)(2.中国科学院物理研究所 北京凝聚态物理国家实验室, 北京 100190)

自旋零能隙半导体是一类具有接近100%的高自旋极化率，同时与工业半导体具有良好兼容特性的新型自旋电子学材料，在自旋注入、自旋晶体管中具有潜在应用前景。从理论计算的电子结构，结合实验的磁性、输运性质能方面对包括Hg2CuTi型，LiMgPdSn四元等比型的Heusler自旋零能隙半导体及其研究进展进行了概述。阐明了Heusler合金中自旋零能隙半导体形成的机制和经验规律，揭示出原子有序、组分调制对自旋零能隙半导体性质的影响。通过对基于Heusler自旋零能隙半导体的自旋注入体系的构建，展望了自旋零能隙半导体的发展趋势和潜在应用。

Heusler合金；自旋零能隙半导体；磁电阻；半金属；自旋注入

Abstract：Spin gapless semiconductors are new class of spintronic materials characterized with nearly fully spin polarization and good compatibilities with the existing semiconductor industry. We reviewed the recent advances of Heusler spin gapless semiconductors, including Hg2CuTi and LiMgPdSn types, from the aspects of first principles calculations and experimental magneto transport properties. We try to illustrate the mechanism and rule guiding for the formation of spin gapless semiconductors in Heulser alloys, and uncover the effect by the atomic order and composition adjust. By constructing the spin injection scheme based on the Heusler spin gapless semiconductor, we give outlook for their development and potential applications.

Key words：Heusler alloys; spin gapless semiconductor; magnetoresistance; half metal; spin injection

1 前 言

自旋电子学致力于实现电子自旋和电荷的双重操控，能够极大提高未来信息存储的密度和处理速度，同时具有非易失性和低能耗的优点。对自旋的操控以及对自旋相关的输运特性研究，需要具有高自旋极化率甚至是能产生纯自旋流的磁性材料，同时还要与现有半导体工业兼容。半金属铁磁体(Half-Metallic Ferromagnets，HMF)[1]是一类具有完全自旋极化的金属材料，以Co2基Heusler合金为代表，其表现出的巨大TMR效应受到了人们的广泛关注[2]。但是半金属作为自旋电子器件的注入端，与半导体基底存在电导失配的问题[3]。自旋零能隙半导体(Spin Gapless Semiconductor, SGS)是理论上兼具100%的完全自旋极化率和(零能隙)半导体特性的材料，在自旋注入、自旋晶体管等中具有应用前景[4,5]。

比较半金属和自旋零能隙半导体的能带结构(如图1)可以看到，半金属中一个自旋方向呈现金属性的能带结构，而在另一个自旋方向出现一个半导体性或绝缘性的能隙，而对于自旋零能隙半导体，在自旋向上方向上打开一个零能隙，在理想情况下，参与输运的电子是单自旋方向的，也就是实现了P=100%的完全自旋极化率。即导带和价带恰好切在费米能级上，另一个自旋方向上与half-metal类似打开一个半导体或绝缘体能隙。

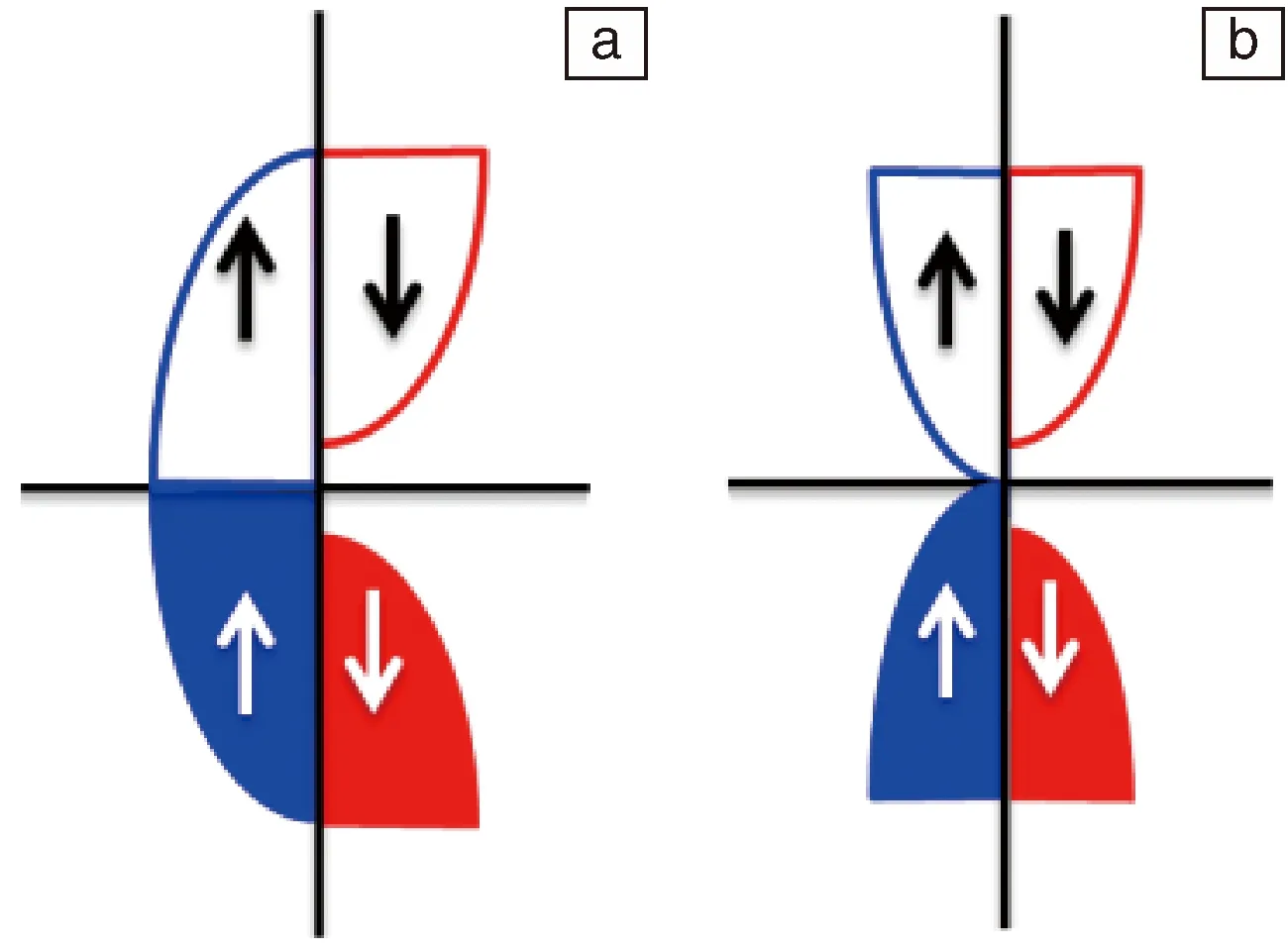
图1 能带结构示意图：(a)半金属；(b)自旋零能隙半导体Fig.1 Schematic of band structure for half-metallic ferromagnet (a) and spin gapless semiconductor (b)

从以上SGS的能带结构可以直接看出：一方面，由于存在与half-metal类似的半导体性能隙，参与输运的载流子也是完全自旋极化的；另一方面，零能隙的特征使得相对于一般半导体而言，载流子激发不需要或只需要很小的能量，有望实现载流子的快速迁移，并具有对外场敏感的特性。类似于二维零能隙材料石墨烯，有望表现出高载流子迁移率、线性大磁电阻以及量子振荡等特殊的输运性能。SGS的这种性质能实现高效地自旋注入和输运。

目前为止，SGS家族主要有Pb基氧化物体系和Heusler合金体系。Heusler合金是一种古老的合金，在1903就被发现并命名。发展至今，已经有超过一千多种化合物，应用在马氏体相变、自旋电子学、超导、拓扑绝缘体多个功能材料领域。本文将就Heusler合金型的自旋零能隙半导体及其研究进展做一个概述。

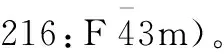
图2 Heusler结构的不同构型：(a) 高有序L21结构；(b)半Heusler C1b结构；(c)B、D位混乱占据的B2结构；(d)A、B、C、D位都混乱占据的A2结构Fig.2 Heusler structure: (a) highly order L21; (b) half-Heusler C1b; (c) B2 structure with B, D site mixed; (d) A2 structure with all sites mixed

另一方面，在实际的Heusler中会存在一定的反占位或无序占位，导致合金有序度下降。如图2c和2d所示，当B、D位上的原子出现混乱占位，形成B2结构；当所有晶位上的原子都混乱占位，为A2结构。在不同的有序度状态下，合金磁性、电性等都可能发生变化，所以在实际的合金制备中，可以通过不同的制备方法和热处理工艺，如甩带快淬、不同温度退火等，来获得不同有序度的样品，以满足不同应用和研究的需求。

2 Hg2CuTi型Heusler自旋零能隙半导体

2.1 Mn2CoAl：块体与薄膜

Hg2CuTi型的Mn2CoAl是Heusler合金中最早被预言并经实验证实的自旋零能隙半导体材料[6]。对Mn2CoAl多晶块体的磁输运性质研究表明[6]，其电阻随温度变化呈现半导体性的负温度系数。这是不同于一般的磁性金属或半金属(half-metal)的。其接近为零的Seebeck系数，以及载流子浓度几乎不随温度变化的依赖关系是零能隙体系的典型特征[7]。在Mn2CoAl中也观测到磁电阻变号现象，以及反常变小的反常Hall系数，通过Berry相的计算，预示了一种电子空穴补偿的机制。

取向的Mn2CoAl薄膜能够用磁控溅射和MBE生长获得[8,9]。图3a显示了在SiO2/Si衬底上生长，沿001方向取向的Mn2CoAl薄膜。磁化曲线(如图3b)显示MCA薄膜强的铁磁性特征。计算得到5 K的饱和磁矩1.94 μB，与理论计算正分体系的1.98 μB基本一致。平行于膜面的热磁曲线显示居里温度高于400 K，通过拟合其居里温度得到Tc～550 K。这与Mn2CoAl块体相比下降了约200 K，分析可能是由于合金成分中磁性元素Co的缺失所导致。

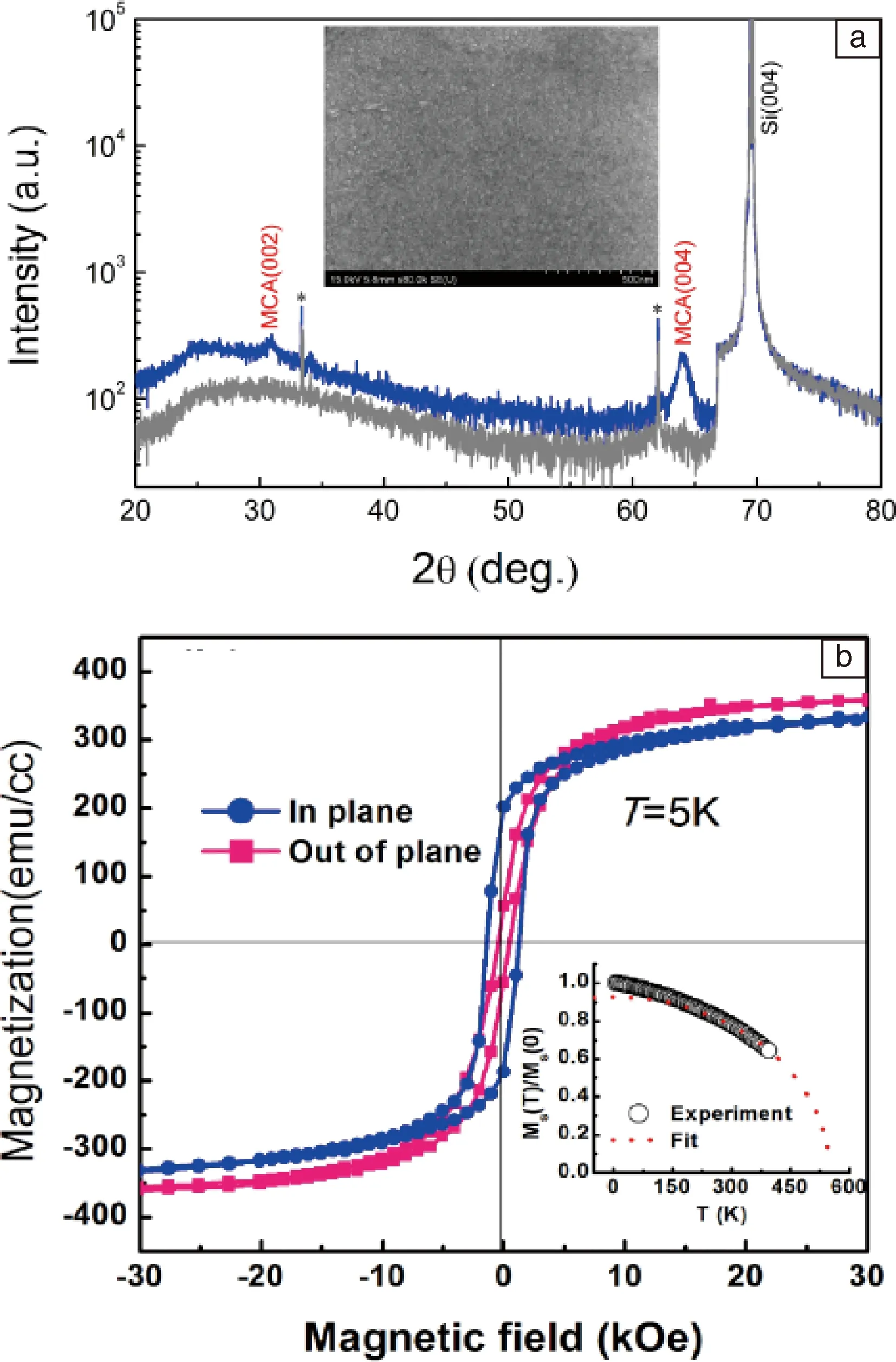
图3 Mn2CoAl薄膜的XRD图谱及SEM照片(a)；薄膜面内和垂直于面的5 K磁滞回线，插图为2 kOe下的热磁曲线(b)Fig.3 XRD and SEM pattern for Mn2CoA film (a); In-plane and out-plane magnetic hysteresis loop at 5 K, inset is thermomagnetization curve under 2 kOe (b)

Mn2CoAl薄膜也显示与块体接近的输运行为。如图4a，其纵向电阻与温度的变化呈现负增长关系，这是典型半导体的特征。同样在MBE生长的Mn-Co-Al薄膜里，ρxx-T曲线在低温也出现拐弯[9]。实际上，在半金属semimetal或窄禁带半导体里面，ρxx-T曲线的拐弯是比较常见的，主要是由于低温下原子无序，缺陷或偏分等产生的杂质能级散射所导致的[10]。对Mn2CoAl薄膜的磁电阻测量结果(如图4b)显示在5 T范围内显示出线性性质，这与Mn2CoAl块体和其他零能隙系统类似[11]。但是相比于块体，薄膜MR值变小，只有百分之零点几，而且在整个温度范围内都为负值，并无变号出现。这种差别主要是由于组分偏离所导致的费米能级移动使得体系的零能隙受到一定程度的破坏[8,12]。另外其MR绝对值随着温度呈现非单调的变化，在50 K达到最大值(图4b的插图)。这种现象在MBE生长的薄膜中也观察到了。考虑到负磁电阻一般是由于磁性体系中的自旋相关散射所导致，随着温度降低而其绝对值升高；另一方面，低温下的偏分或杂质散射会导致一个正向磁电阻的叠加，使得整体的MR绝对值减小，这种竞争行为导致MR在50 K极值的出现。

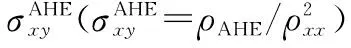
2.2 Ti2基自旋零能隙半导体的预测

对包含了Mn2CoAl在内的一系列Hg2CuTi型Heusler合金进行系统的理论计算[13]，预测出了几类新的体系，主要是Ti2基材料，包括Ti2MnAl, Ti2CoSi以及通过晶格畸变得到的磁补偿型自旋零能隙半导体Ti2CrSi[14]和Ti2CrSn[15]。图5中显示了其中一些合金的态密度图，引自文献[13]。可以看到虽然自旋朝上的零能隙都存在，但是对于Ti2基Heusler合金在自旋向下部分其费米面切在能隙底部或顶部，使得其半金属能隙易受温度扰动，不利于实际应用。另外需要注意的是这些材料的总价电子数都为18或21，其中隐含的规律将在下文说明。

3 LiMgPdSn型四元等比Heusler自旋零能隙半导体

3.1 理论预测

对四元等比Heusler自旋零能隙半导体的发现是首先在理论预测上实现的。通过对大量四元等比结构的扫描，获得了CoFeMnSi、CoFeCrAl、CoMnCrSi和CoFeVSi等新型自旋零能隙半导体体系[16]。图6给出了其中CoFeCrAl不同自旋方向的能带结构。可以看到自旋向下方向，在Γ点处存在一个约0.5 eV的能隙，而在自旋向上方向，如绿线所示，能带在k空间的K点，L点(价带)和X点(导带)恰好切在费米能级上，这也对应了(b)图中态密度的低谷处。闭合零能隙的存在使得CoFeCrAl成为SGS的候选者，而与普通的半金属铁磁体相区别。

从半金属的研究中可知，当某一自旋方向存在能隙时，合金化合物的总磁矩为整数，遵循Slater-Pauling(SP)

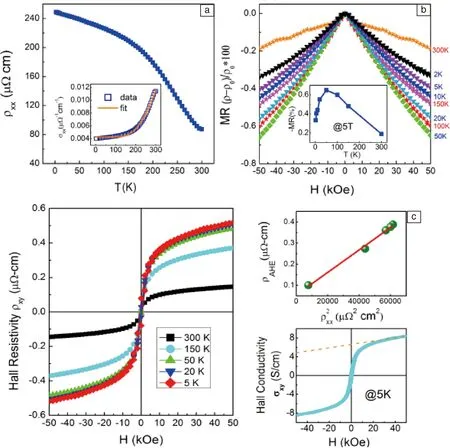
图4 Mn2CoAl薄膜的电阻-温度变化曲线(a)，不同温度下的磁电阻(b)以及反常Hall效应(c)Fig.4 ρxx-T curve (a), magnetoresistance (b) and anomalous hall effect (c) for various temperatures

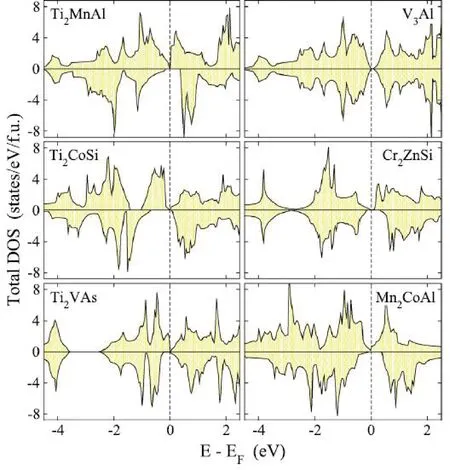
图5 一些合金的能态密度图[13]Fig.5 Density of states for above alloys [13]

图6 CoFeCrAl的电子结构：(a)自旋向上、(c)自旋向下的能带及(b)自旋分辨的能态密度图；能带右侧为d轨道杂化能级的简约表示Fig.6 Band structure and density of states (DOS) of CoFeCrAl: (a) majority spin, (b) density of states, (c) minority spin. The irreducible representations of d-orbital hybridized bands are given for the Г-point

法则[17]。在四元等比Huesler合金中能带杂化类型不变，所以也符合这个规律。因此，随着价电子数的不同，大部分化合物的总磁矩遵循广义的SP法则：以总价电子数等于21为界限其总磁矩遵循M=Nv-18或M=Nv-24(Nv为总价电子数)[18]。值得注意的是，处于边界处的21价电子数体系较为特殊，若自旋极化仍能保持，那么多子和少子方向上费米能级都处于能隙之中，这对应的就是磁性半导体。与前面提到的Ti2基自旋零能隙半导体类似，在四元等比中CoVTiAl，FeCrTiAl为可能的磁性半导体材料。

因此，目前Heusler型的SGS候选材料都具有21，26或28个价电子数。对这一规律的深入探讨需要对Heusler型半金属铁磁体中的原子杂化以及半金属能隙的由来进行讨论，并且对于自旋零能隙半导体，不仅要考虑自旋向下的杂化，同时还应考虑自旋向上能级杂化的情况。

如图7所示，自旋向下的能级杂化与半金属中相同，最终形成的一系列简并能级，eg、eu，tg、tu等。当费米面处于如图示的能隙位置时，对应自旋向下占据12个电子的情况，符合M=Nv-24 SP法则。自旋向上的能级杂化具有类似性。SGS的能带结构要求在自旋向下方向存在零能隙，换句话说，就是要求在自旋向下也存在一个能隙，只是能隙恰好闭合，切在费米面处。结合上述的杂化图像，要实现零能隙，费米面应落入两个简并的能级之间，才能保证能带不被费米面切过。也就是说，费米面或落在如图示的2eu和2eg之间，或是在2eg和3t2g之间，对应的总价电子数为26或28。当落于3t1u和3t2g之间，此时他们对应的总价电子数为21。以图6中的CoFeCrAl为例，费米能级位于2eg和2eu轨道之间，同时2eu的顶端和2eg的底端恰好切在费米能级上，因此表现SGS的性质。如果总价电子数增多或减少一个，就意味着能带会下移或上移，使得两侧的简并能级穿过费米面，从而导致零能隙不可能存在，因此推断价电子数为25或27的体系不能成为SGS的候选者。

这一规律为后期的更多的理论预测所证实[19]。但注意这只是寻找自旋零能隙半导体的必要条件，并不是充分条件。当用同族的元素相互替代，总价电子数并不改变，但是杂化的强弱不同会导致能带的细节发生变化，影响或破坏SGS的能带结构。例如用同主族的Ga或In取代CoFeCrAl中的Al，自旋向上的零能隙结构能够较稳定地维持，但是自旋向下的半金属能隙却由于主族杂化作用的减弱而被破坏[16]。另一方面，通过拉伸或压缩晶格，或四方畸变的方法，能够精细调控能带达到较理想的零能隙结构。

图7 四元等比Heusler合金中A、B、C位原子d电子能级杂化示意图，左为自旋向下，右为自旋向上。红线表示费米面位置Fig.7 Sketch of d-orbital hybridizations between the transition atoms at different sites in the quaternary Heusler compound (left for spin-down, right for spin-up). The red line indicates the location of the Fermi level

3.2 CoFeCrAl块体的结构、磁性与输运性质

在预言的四元等比自旋零能隙半导体中，CoFeCrAl(Ga)以及CoFeMnSi由于具有较高稳定性受到大量关注[20-22]。但是四元等比合金并不容易制备如理论计算的高有序相。一般对于高有序的L21及Hg2CuTi结构，如前所述，会出现B2结构和A2混乱。图8中显示的三组CoFeCrAl样品中只出现(200)超晶格峰，没有观察到(111)峰，预示可能存在A/C(Co/Fe)或B/D(Cr/Al)位混乱占位的情况。经过甩带和退火的样品，其XRD峰没有明显变化，说明这两种方式在体系中并未明显改善原子有序占位。这可能是因为主族元素Al的共价作用较弱，有序化能力不够强，不容易形成高有序的结构。

尽管有序度并未明显改善，但是原子的反占位情况会由于这两种不同的处理方式发生改变，从而导致图8c～8e中CoFeCrAl退火和甩带样品电输运性质的截然不同。对于退火样品，电阻随温度升高而升高，是一种金属性的行为。其磁电阻MR在整个温度范围内都为负值，与一般磁性金属中类似：其磁电阻由自旋相关的散射所主导，随着温度的降低MR绝对值增大。而对于甩带样品，电阻随温度变化表现出负的温度系数，表现出一种受激发的半导体行为。其MR与退火样品完全相反，表现出正的近线性的磁电阻行为。对于零能隙半导体，线性磁电阻是其一个显著特征。而正的磁电阻一般出现在非磁性体系，是受经典的洛伦兹力占主导的散射行为，这在其他的自旋零能隙半导体体系如掺Co的PbPdO2[5]和Mn2CoAl[6]中均观察到了。虽然CoFeCrAl表现出类似于半导体的输运特征，但是其电阻率大小仍在金属范围(μΩ·m)。载流子浓度很大，导致其磁电阻值非常小(<1%)，很难有实际的应用。进一步提高有赖于其有序度的进一步提升。

图8 CoFeCrAl不同热处理下的结构(a),电阻(b)和(d)及磁电阻(c)和(e)随温度变化Fig.8 Crystal structure (a), temperature dependence of resistivity (b) and (d) as well as magnetorisistence (c) and (e) for CoFeCrAl under different heat treatments

3.3 高迁移率自旋零能隙半导体体系的设计

前述Mn2CoAl以及四元等比Heusler型自旋零能隙半导体等在费米面附近的电子类型都为d电子，一定温度对能带的扰动很容易产生较大的载流子浓度，造成迁移率过低。同时d电子较大的有效质量也成为抑制迁移率的原因。考虑s电子或p电子在实际金属系统相比d电子更为巡游，所以其能带也更为扩展，对应较小的有效质量。较为典型的例子是石墨烯的能带结构，为线性的色散关系，有效质量很小，迁移率很大。

要实现这种所谓轻电子型的自旋零能隙半导体(如图9a)设计，首先应考虑在Heusler合金中是否存在高迁移率的情形。根据 Shekhar等人[23]及中国科学院物理研究所[24]的相关工作，含有较重稀土金属的半Heusler合金体系如YPtSb、LuPtBi等在实验上观测到很高的载流子迁移率。这类半Heusler合金的迁移率行为与其特殊的电子结构有关，强烈的自旋轨道耦合使得能带在费米面附近发生翻转，形成类似自旋零能隙半导体中的近零能隙结构。本课题组对类似体系的深入研究发现，其高迁移率的机制即为参与导电的电子类型为有效质量很小的sp电子。通过对能级杂化的分析，本课题组发现能形成sp电子导电的一个重要因素是La系重元素引起的d能带下移所致。

考虑加入稀土元素，图9b中显示了利用第一性原理计算LaCoCrGa的能带结构，其中sp态电子的占据分数在费米面附近显著增加，这与d电子主导的类型是明显不同的。其能带在费米面处呈现接近线性色散关系，这有可能极大提高自旋零能隙半导体的载流子迁移率[25]。

图9 具有线性散射关系的自旋零能隙半导体能带构型(a)；新型轻电子导电Heusler自旋零能隙半导体LaCoCrGa的能带及其中sp 电子、d电子占据分数(b)Fig.9 Band sketch of linear-type spin gapless semiconductor (a). Calculated band structure of LaCoCrGa, with resolved sp and d occupation (b)

4 基于Heusler自旋零能隙半导体的自旋注入结构

4.1 自旋注入结构构建

自旋注入的最基本结构是磁性材料/半导体界面。传统的自旋注入利用的是普通铁磁金属/半导体(FM/SC)直接接触的界面(也称欧姆接触)，例如Fe/GaAs界面。但是实验结果显示这种结构的自旋注入效率(一般被定义为半导体中传输的电子自旋极化率)很低，最好的也只有百分之几[26]。其注入效率主要受到两方面的限制：一方面是由于金属与半导体界面电导率不匹配所引起的，也称之为Schmidt障碍[27]；另一方面由于传统铁磁金属本身的自旋极化程度。接近半金属铁磁体(HMF)虽然具有100%自旋极化，电导失配问题仍然存在，并没有达到预期的高自旋注入[3]。如果用同样具有完全自旋极化的自旋零能隙半导体的一个新型自旋注入体系，由于它理论上不但具有与HMF一样几乎100%的自旋极化率，而且其本身的半导体特性使得它能有效地克服电导失配问题，有望提高自旋注入效率。

理论上可以通过超晶格结构模拟自旋注入的异质结体系，只要层数达到足够多，能够在远离界面的中心部分保持块体的性质就可以保证模型的有效性。因此通过构建如图10的超晶格模型，可以模拟在自旋零能隙半导体和半导体界面自旋极化的变化[28]。选取的衬底分别为非磁性的Heusler合金Fe2VAl，在实验上已经证实了其半导体性[29]和典型半导体GaAs。图10显示了沿(100)方向构建的Mn2CoAl/Fe2VAl 超晶格结构和沿(110)方向构建的Mn2CoAl/GaAs结构。由于Mn2CoAl和Fe2VAl具有完全相同的晶体结构和原子占位情况，沿(100)方向堆积时原子占位情况不改变，界面变化较小；而对于GaAs，晶体结构相同但是单胞中的原子数减半，所以界面附近变化较大，需要考虑更多层的原子。计算中超胞的面内晶格常数(a,b)固定与衬底一致，而沿堆垛方向c的晶格参数通过人工优化得到。

图10 自旋零能隙半导体作为自旋注入源与半导体形成异质结结构(a)；用于第一性原理计算的超晶格结构：沿(100)方向的[Mn2CoAl/Fe2VAl]2 单胞(左)；沿(110)方向的[Mn2CoAl/GaAs]4 单胞(右)，中间为Mn2CoAl 和GaAs的晶体结构(b)Fig.10 DOS scheme of SGS (up) and conventional semiconductor (down), with a sketch of our calculation model of SGS/SC heterostructure (a); The superlattice primitive cells of [Mn2CoAl/Fe2VAl]2 with (100) interface (left) and [Mn2CoAl/GaAs]4 with (110) interface (right) used for the first principles calculations, the crystal lattice of Mn2CoAl and GaAs are given in the middle panel (b)

4.2 Mn2CoAl/Fe2VAl (GaAs)异质结

构建异质结需要考虑界面的结合方式。从图10中可以看到异质结界面层可以有两种类型：一是Co-Mn/V-Al与Mn-Al/Fe-Fe(由于超晶格是一种周期性的交替结构，这两个界面必然成对出现)，另一种是Co-Mn/Fe-Fe与Mn-Al/V-Al。若界面层组成单元表现为半导体和铁磁注入极的过渡，例如此处的Co-Mn/V-Al (Mn-Al/Fe-Fe)，对应的化合物为CoMnVAl和Fe2MnAl，分别具有半导体性和铁磁性，称之为建设型界面，有利于保持整个超晶格的自旋极化。而不具备这种条件的通常称之为破坏型界面，如此处的Co-Mn/Fe-Fe(Mn-Al/V-Al)。此外从能量的角度看，建设型界面的总能比破坏型界面要低，能够更加稳定地存在[3]。在GaAs中类似，Co-Ga (Al-As)界面更稳定。

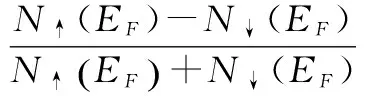
图11 超晶格[Mn2CoAl/Fe2VAl]4 (a)及 [Mn2CoAl/GaAs]4(b)不同层的磁矩和自旋极化率Fig.11 Layer-resolved magnetic moment and spin polarization of [Mn2CoAl/Fe2VAl]4 (a) and [Mn2CoAl/GaAs]4 (b) superlattices

5 结 语

本文对包括Hg2CuTi型以及LiMgPdSn型Heusler自旋零能隙半导体的理论以及实验结果进行了综述。自旋零能隙半导体的预测，可以借鉴半金属的能带杂化图像，具有较简明的经验框架。Heusler自旋零能隙半导体的发展和在自旋电子学中的应用，还需要大量实验的进一步支撑。实现其理论预测的性能，需要对Heusler合金中的反占位和有序度进行有效的调控。其中CoFeCrAl(Ga)和CoFeMnSi等在实验上已经观测到较高的自旋极化率。而Mn2CoAl薄膜的成功生长，为后期进一步制作自旋零能隙半导体自旋注入器件打下了基础。另外为实现自旋零能隙半导体的高迁移率，可以考虑在其中掺入稀土元素。实现自旋零能隙半导体实现的条件虽然较苛刻，但是Heusler合金的大范围可调控性，为进一步实现磁性半导体的提供了重要思路。

References

[1] de Groot R A, Mueller F M, Engen P G,etal.PhysicsReviewLetters[J], 1983, 50 (25): 2024-2027.

[2] Wang W H, Sukegawa H, Shan R,etal.AppliedPhysicsLetters[J], 2009, 95 (18): 182502.

[3] Chadov S, Graf T, Chadova K,etal.PhysicalReviewLetters[J], 2011, 107 (4) : 047202.

[4] Wang X L.PhysicsReviewLetters[J], 2008, 100 (15): 156404.

[5] Wang X L, Peleckis G, Zhang C,etal.AdvancedMaterials[J], 2009, 21 (21): 2196-2199.

[6] Ouardi S, Fecher G H, Felser C.PhysicsReviewLetters[J], 2013 (10), 110: 100401.

[7] Tsidilkovski I M.ElectronSpectrumofGaplessSemiconductors[M]. Heidelberg: Springer-Verlag, 1997.

[8] Xu G Z, Du Y, Zhang X M,etal.AppliedPhysicsLetters[J], 2014, 104 (24): 242408.

[9]Jamer M E, Assaf B A, Devakul T,etal.AppliedPhysicsLetters[J], 2013, 103 (14): 142403.

[10] Gofryk K, Kaczorowski D, Plackowski T,etal.PhysicalReviewB[J], 2005, 72 (14): 094409.

[11] Du Y, Xu G Z, Zhang X M,etal.EPL[J], 2013, 103(3): 37011.

[13] Skaftouros S, Ozdogan K, Sasioglu E,etal.AppliedPhysicsLetters[J], 2013, 102 (2): 022402.

[14] Wang L, Jin Y J.JournalofMagnetismandMagneticMaterials[J], 2015, 385: 55-59.

[15] Jia H Y, Dai X F, Wang L Y,etal.JournalofMagnetismandMagneticMaterials[J], 2014, 367: 33-39.

[16] Xu G Z, Liu E K, Du Y,etal.EPL[J], 2013, 102 (1): 17007.

[17] Galanakis I, Dederichs P, Papanikolaou N.PhysicalReviewB[J], 2002, 66 (9): 174429.

[18] Galanakis I, Mavropoulos P, Dederichs P H.JournalofPhysicsD:AppliedPhysics[J], 2006, 39 (5): 765-775.

[20] Bainsla L, Mallick A I, Raja M M,etal.PhysicalReviewB[J], 2015, 92 (4): 045201.

[21] Nehra J, Sudheesh V D, Lakshmi N,etal.PhysicalStatusSolidiRRL[J], 2013, 7(4): 289.

[22] Kharel P, Zhang W, Skomski R,etal.JournalofPhysicsD:AppliedPhysics[J], 2015, 48 (24): 245002.

[23] Shekhar C, Ouardi S, Nayak A,etal.PhysicalReviewB[J], 2012, 86 (15): 155314.

[24] Hou Z P, Wang W H, Xu G Z,etal.PhysicalReviewB[J] 2015, 92 (23): 235134.

[25] Xu G Z, Zhang X M, Hou Z P,etal.EPL[J],2015, 111(6):68003.

[26] Hammar P R, Bennett B R, Yang M J,etal.PhysicalReviewLetters[J], 1999, 83 (1): 203-206.

[27] Schmidt G, Ferrand D, Molenkamp L W.PhysicalReviewB[J], 2000, 62 (8): R4790-R4793.

[28] Xu G Z, You Y R, Gong Y Y,etal.JournalofPhysicsD:AppliedPhysics[J], 2017, 50(10): 105003.

[29] Nishino Y, Kato M, Asano S,etal.PhysicalReviewLetters[J], 1997, 79 (10): 1909-1912.

(编辑 吴 琛)

Spin Gapless Semiconductors Based on Heusler Alloys

XU Guizhou1, XU Feng1, WANG Wenhong2

(1.Nanjing University of Science and Technology, Nanjing 210094, China)(2.Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China)

O469

A

1674-3962(2017)09-0616-09

2017-01-20

国家自然科学基金资助项目(11604148)

徐桂舟，女，1988年生，博士，讲师

徐 锋，男，1978年生，教授，博士生导师，Email: xufeng@njust.edu.cn

10.7502/j.issn.1674-3962.2017.09.02