基于范成法加工摆线内齿轮副的齿根过渡曲线分析

贵新成，李红勋，李立顺，牛四波

(1.陆军军事交通学院 研究生管理大队，天津 300161；2.陆军军事交通学院 国家应急交通运输装备工程技术研究中心，天津 300161；3.68117部队，兰州 730070)

基于范成法加工摆线内齿轮副的齿根过渡曲线分析

贵新成1，李红勋2，李立顺2，牛四波3

(1.陆军军事交通学院 研究生管理大队，天津 300161；2.陆军军事交通学院 国家应急交通运输装备工程技术研究中心，天津 300161；3.68117部队，兰州 730070)

精确的齿根过渡曲线对于齿轮弯曲强度的评价具有重要意义。结合机械生产实际，对现有常用的齿轮加工方法及其过渡曲线形式进行分析，从中选取具有代表性的加工方案，据此建立摆线齿轮加工刀具的齿廓模型。根据齿轮啮合理论，推导摆线内齿轮副齿根过渡曲线的参数方程，实现其齿根过渡曲线的精确建模和轮齿弯曲强度的准确计算。

摆线齿轮；过渡曲线；范成法

Abstract：A precise root fillet curve has great significance for the evaluation of gear bending strength. According to the actual machinery production, the paper firstly analyzes the common gear machining method and its root fillet curve. Then, it selects a typical machining scheme and establishes the teeth profile model of cycloid gear cutting tool. Finally, it deduces the parametric equation of root fillet curve of internal cycloid gear based on gear meshing theory, and realizes precise modeling and accurate calculation of teeth bending strength.

Keywords：cycloid gear； fillet curve; generating method

齿轮是现代机械工业中非常重要的一种传动基础元件，尽管摆线齿轮早于渐开线齿轮，但渐开线齿轮中心距可分、切齿刀具简单且具有通用性，因而应用最广，几乎占据了除钟表工业以外的整个机械领域[1-3]。近年来，随着制造加工技术的发展，摆线啮合又获得了生机，并凭借其自身优势广泛用作摆线针轮、Roots轮、泛摆线齿轮等齿形，特别是某新型内啮合摆线齿轮的出现，有望改变传统复合摆线齿轮只用于轻载、分度等领域的局面，可提供较高的承载能力。而高承载能力的一个重要方面就是具备较高的弯曲强度。由于轮齿弯曲强度与齿根过渡曲线圆弧半径大小密切相关，且该圆弧是在齿廓加工过程中形成的，所以齿根过渡曲线和它的圆弧半径直接取决于齿轮的加工方法、刀具的类型及其齿顶形状[4]。以往的研究大多针对外齿轮，对于内齿轮的相关研究较少。为避免齿根过渡曲线的不确定性对齿轮弯曲强度的影响，有必要对摆线内齿轮副的加工工艺和刀具齿廓进行研究，并得到相应过渡曲线的定量描述[5-6]。

1 过渡曲线的形式与刀具齿廓

1.1过渡曲线的形式

根据文献[7]，目前常见的齿根过渡曲线主要有以下5种。

(1)由齿顶为单圆角齿条型刀具滚切加工时，过渡曲线是一整段延伸渐开线的等距线。

(2)由齿顶为双圆角齿条型刀具滚切加工时，过渡曲线是延伸渐开线的等距线，而中间的是齿根圆弧。

(3)由齿顶为单圆角齿轮型刀具滚切加工时，过渡曲线是一整段延伸外摆线的等距线。

(4)由齿顶为双圆角齿轮型刀具滚切加工时，过渡曲线是延伸外摆线的等距线，而中间的是齿根圆弧。

(5)由成形铣刀仿形加工时，过渡曲线是一整段圆弧。

然而，以上所述都是针对外齿轮的加工，对于内齿轮，通常只能用齿轮插刀加工，故其过渡曲线为一整段缩短内摆线的等距线或两段缩短外摆线的等距线加中间一段齿根圆弧。由于成形法加工的精度不高、效率也低，一般很少使用，所以在齿轮加工中通常都采用范成法，它是利用齿轮啮合时其共轭齿廓互为包络线的原理加工的。事实上，齿顶为单圆角的刀具可认为是齿顶为双圆角刀具的特殊情况。因此，为研究方便又不失代表性，摆线外齿轮采用齿条型刀具加工，摆线内齿轮采用齿轮型刀具加工，且它们的齿顶均为双圆角。

1.2刀具齿廓的参数

1.2.1 齿条型刀具

用以加工摆线齿轮的齿顶为双圆角的齿条型刀具齿廓如图1所示。各相关参数之间关系为

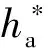
假设已知的齿条型刀具齿顶部分摆线的参数方程为

式中：rca为滚圆半径；t为参变量。

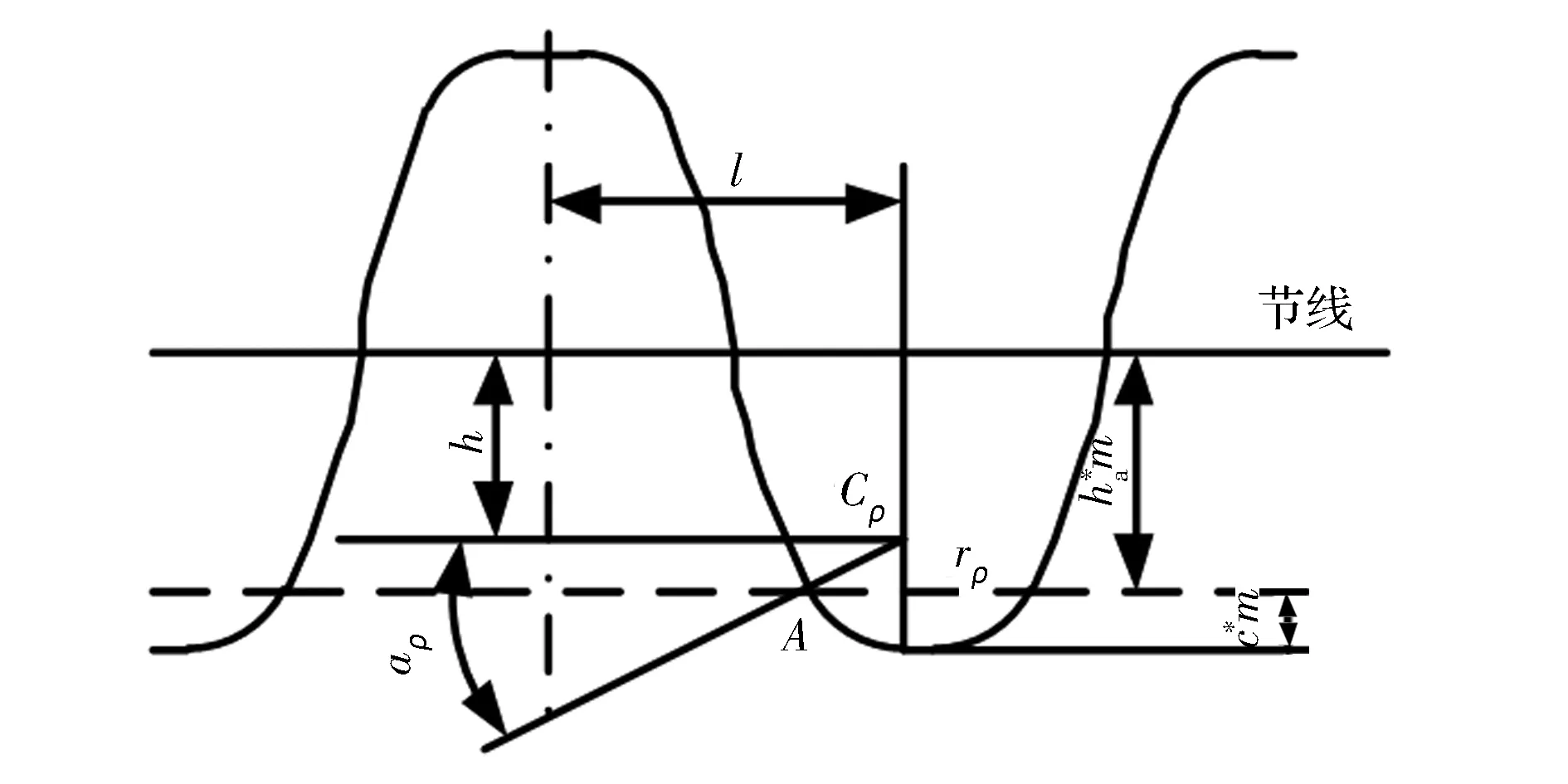
图1 摆线齿齿条型刀具齿廓

记齿条型刀具齿顶部分摆线与圆角切点A的坐标为(xc0,yc0)，则有

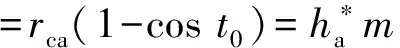
即

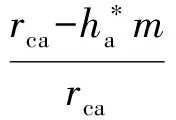
于是，齿顶部分摆线与圆角切点的横坐标为

xc0=rca(t0-sint0)

根据微分法，易得齿条型刀具齿顶部分摆线与圆角切点的法线倾角为

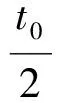
1.2.2 齿轮型刀具

用以加工摆线齿轮的齿顶为双圆角的齿轮型刀具齿廓如图2所示。

图2 加工摆线齿轮的齿轮型刀具齿廓

如图3所示，假设已知的齿轮型刀具齿顶部分外摆线的参数方程为

式中：rc为刀具节圆半径；rca为滚圆半径；t为参变量。

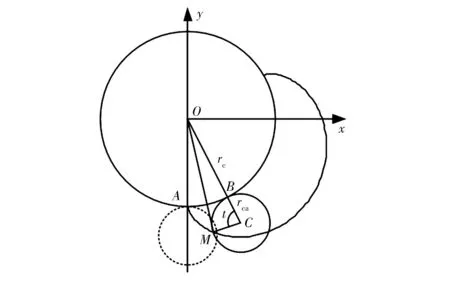
图3 外摆线的形成及其参数关系

∠AOM=∠AOC-∠COM=

(1)

于是，有

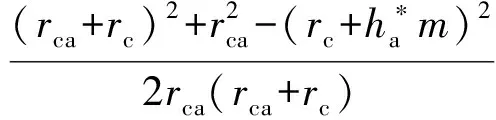
根据微分法，易得齿顶部分摆线与圆角切点的法线倾角为

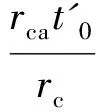
在图2中，以齿轮刀具中心Oc为坐标原点，以OcS为y轴，x轴与之垂直，设齿轮型刀具圆角圆心Cρ的坐标为(xCρ，yCρ)，则有

(2)

又因为

(3)

联立式(2)、式(3)，便可求得刀具圆角圆心Cρ的坐标(xCρ，yCρ)和刀具圆角半径r'ρ。

在ΔTOcCρ中，由余弦定理可得

由图2、图3以及式(1)，得

于是，可求得

式中zc为齿轮刀具的齿数。

2 摆线内齿轮副的齿根过渡曲线方程

2.1齿条型刀具加工摆线外齿轮

用齿条型刀具加工外齿轮时，刀具加工节线与外齿轮节圆相切并作相对纯滚动。如图4所示：Ρ为节点；nn为刀具圆角与过渡曲线接触点的公法线；α'为nn与刀具加工节线之间的夹角。

图4 齿条型刀具加工外齿轮的过渡曲线

取图4中的坐标系Oxy，易得延伸渐开线等距线的参数方程为

(4)

式中，α'与φ之间有如下关系：

r1φ1=htanα'+l

(5)

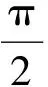
2.2齿轮型刀具加工摆线内齿轮

用齿轮插刀加工内齿轮时，刀具加工节线与内齿轮节圆相切并作相对纯滚动。如图6所示：P为节点；nn为刀具圆角与过渡曲线接触点的公法线；tt为两节圆的公切线；α'为nn与tt之间的夹角。

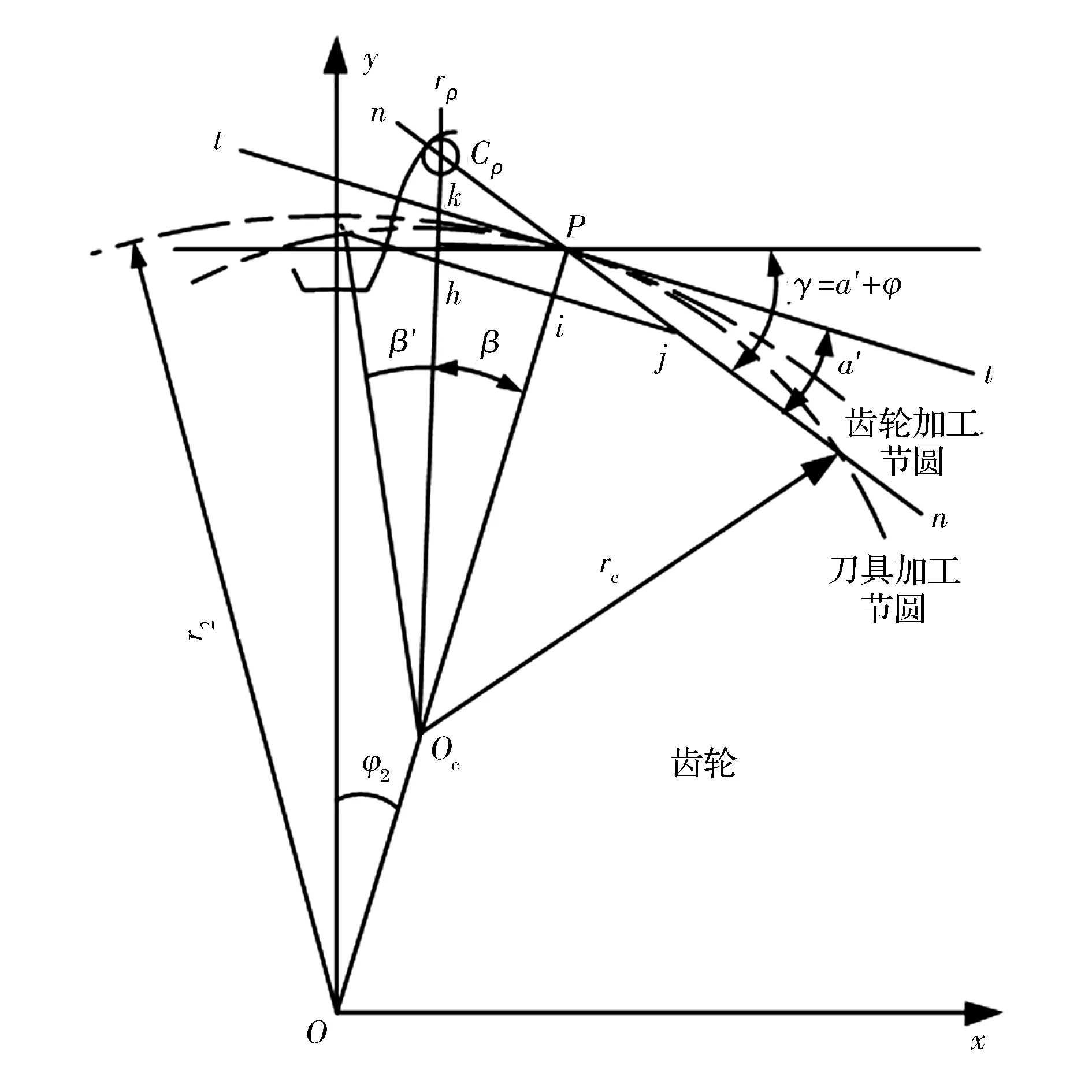
图5 齿轮型刀具加工内齿轮的过渡曲线

取图5中的坐标系Oxy，易得缩短内摆线等距线的参数方程为

(6)

式中，β与φ之间有如下关系

式中z2是内齿轮的齿数。

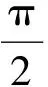
3 计算实例

现以一对内啮合摆线齿轮的范成加工为例，对其齿根过渡曲线和齿廓曲线进行图像化表达，有关参数见表1。综合上述分析，利用Matlab软件编写相关的计算程序，并分别绘制摆线内、外齿轮的过渡曲线以及完整的单齿齿廓，如图6～图9所示。

由图7和图9可知，外齿轮的齿根过渡曲线与齿根部分的内摆线、内齿轮的齿根过渡曲线与齿根部分的外摆线均在交点处平滑过渡，由此可以验证上述方程推导和程序编制的正确性。

表1 内啮合摆线齿轮副的有关参数

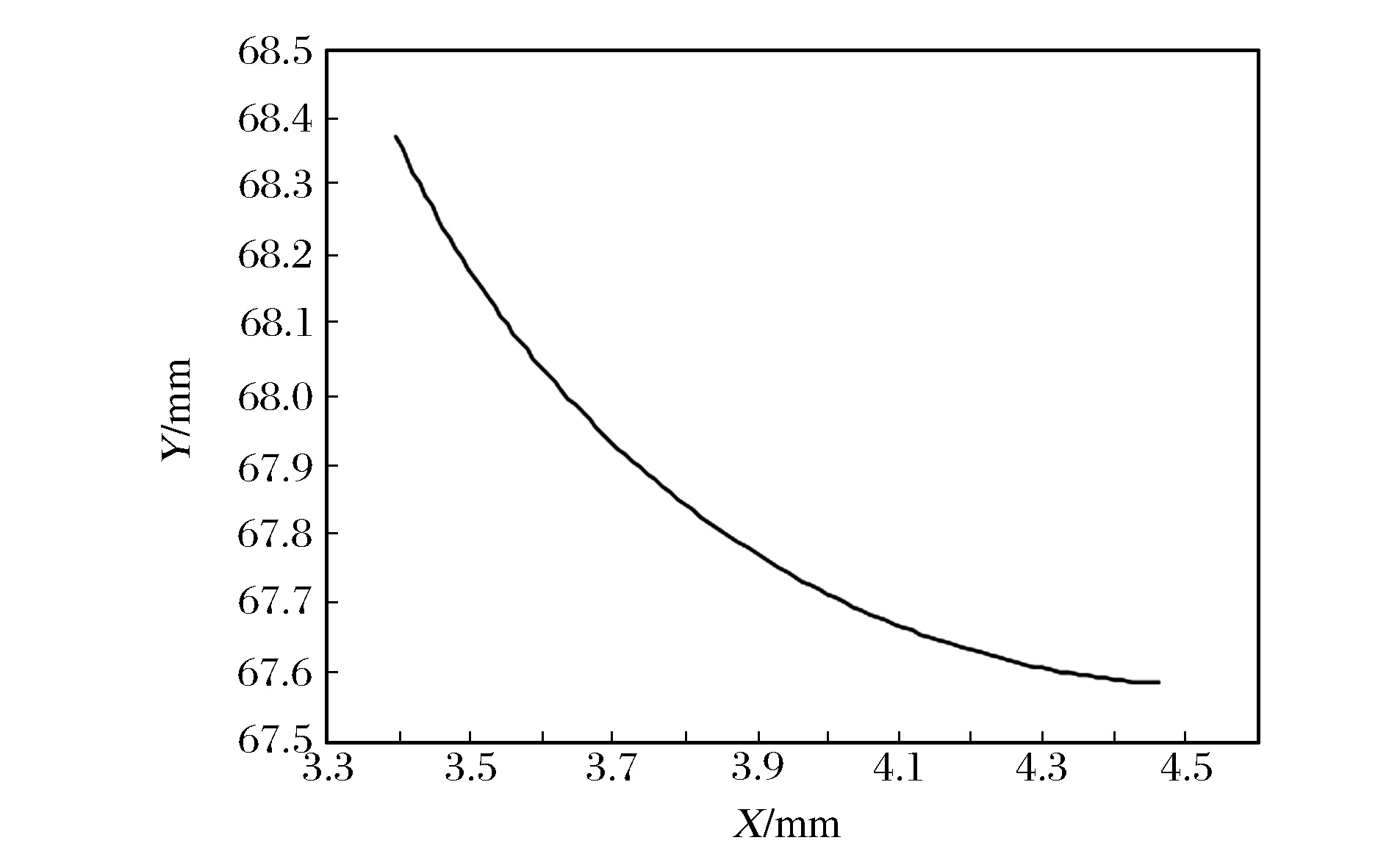
图6 摆线外齿轮的过渡曲线

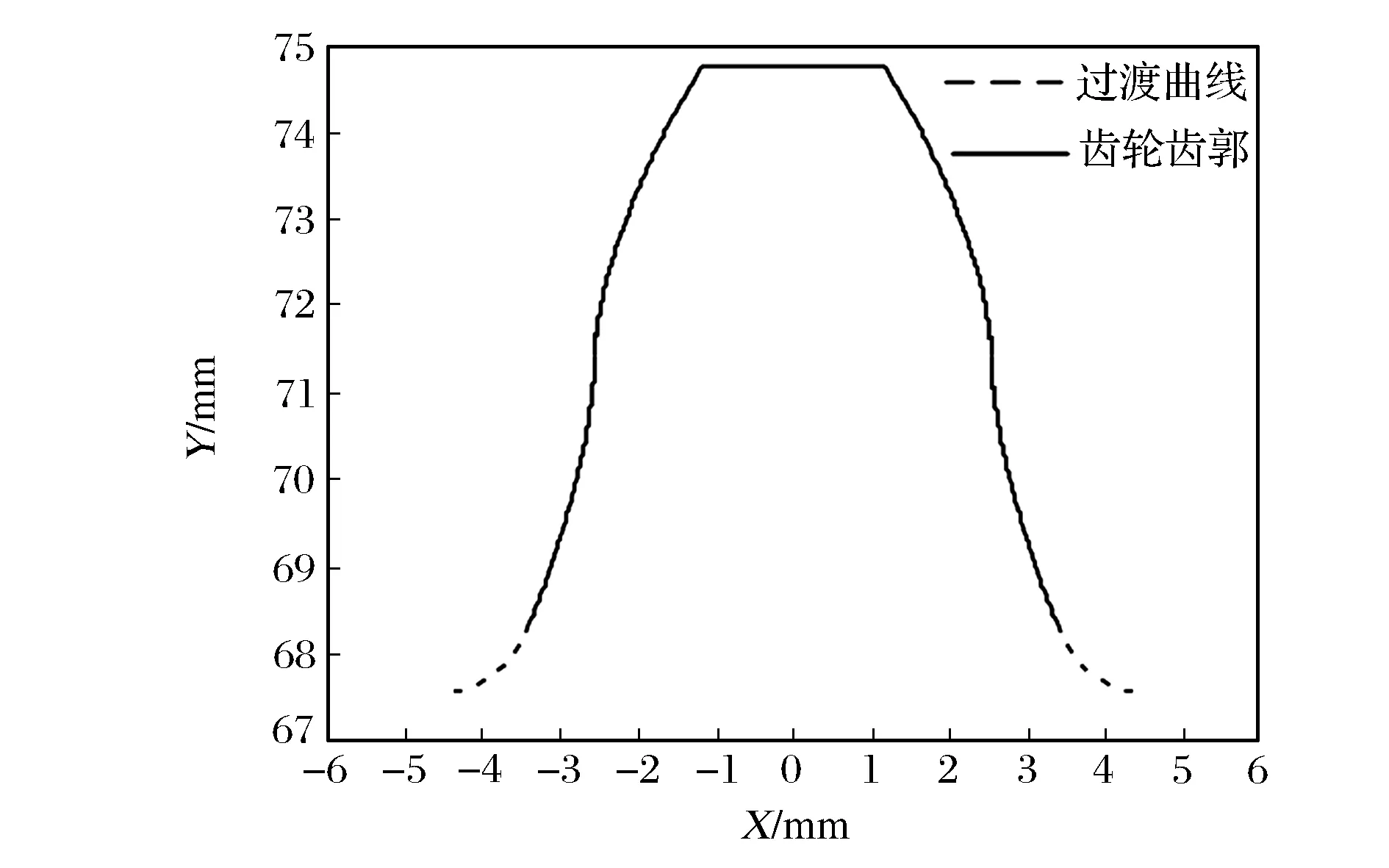
图7 摆线外齿轮的完整齿廓

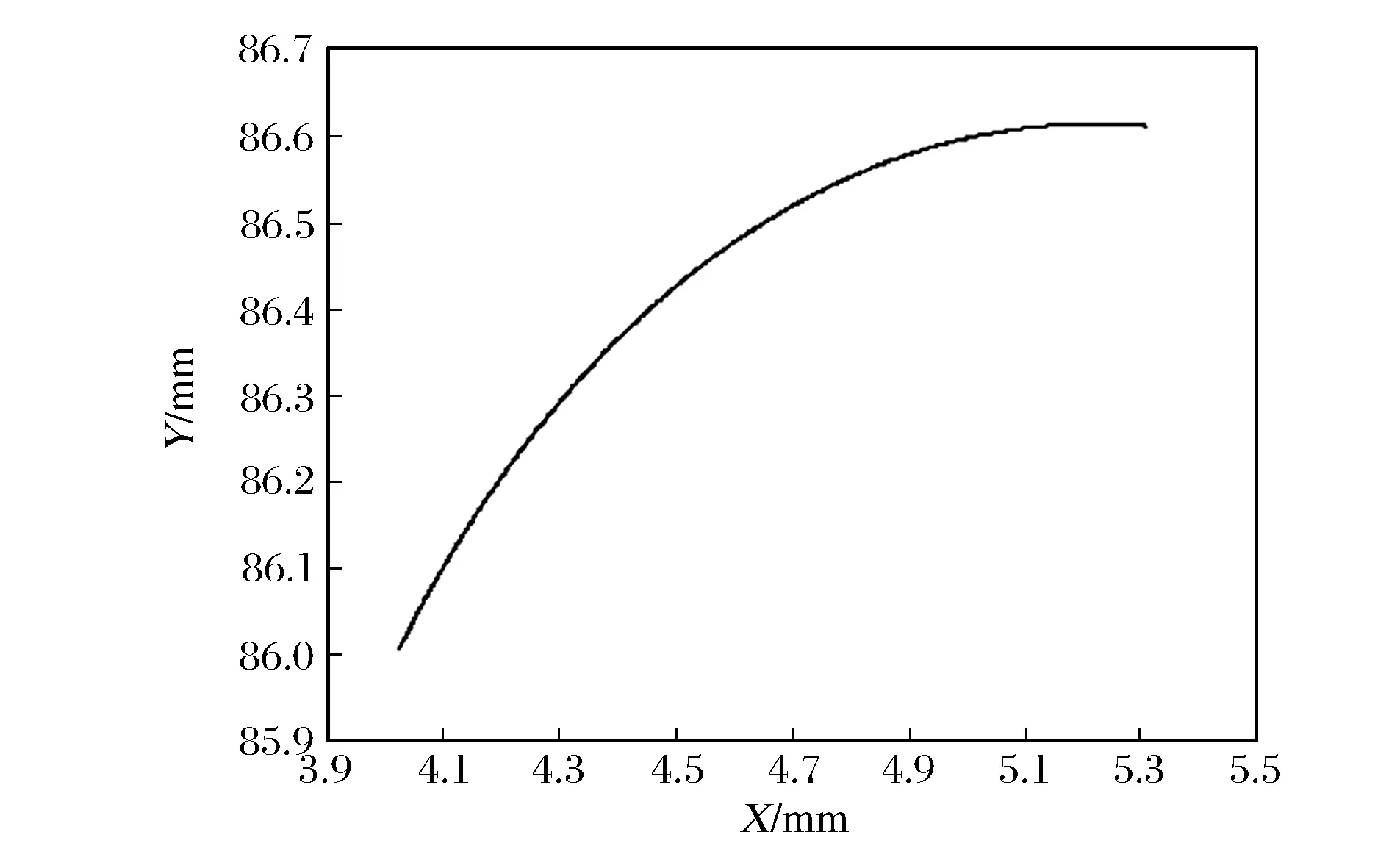
图8 摆线内齿轮的过渡曲线

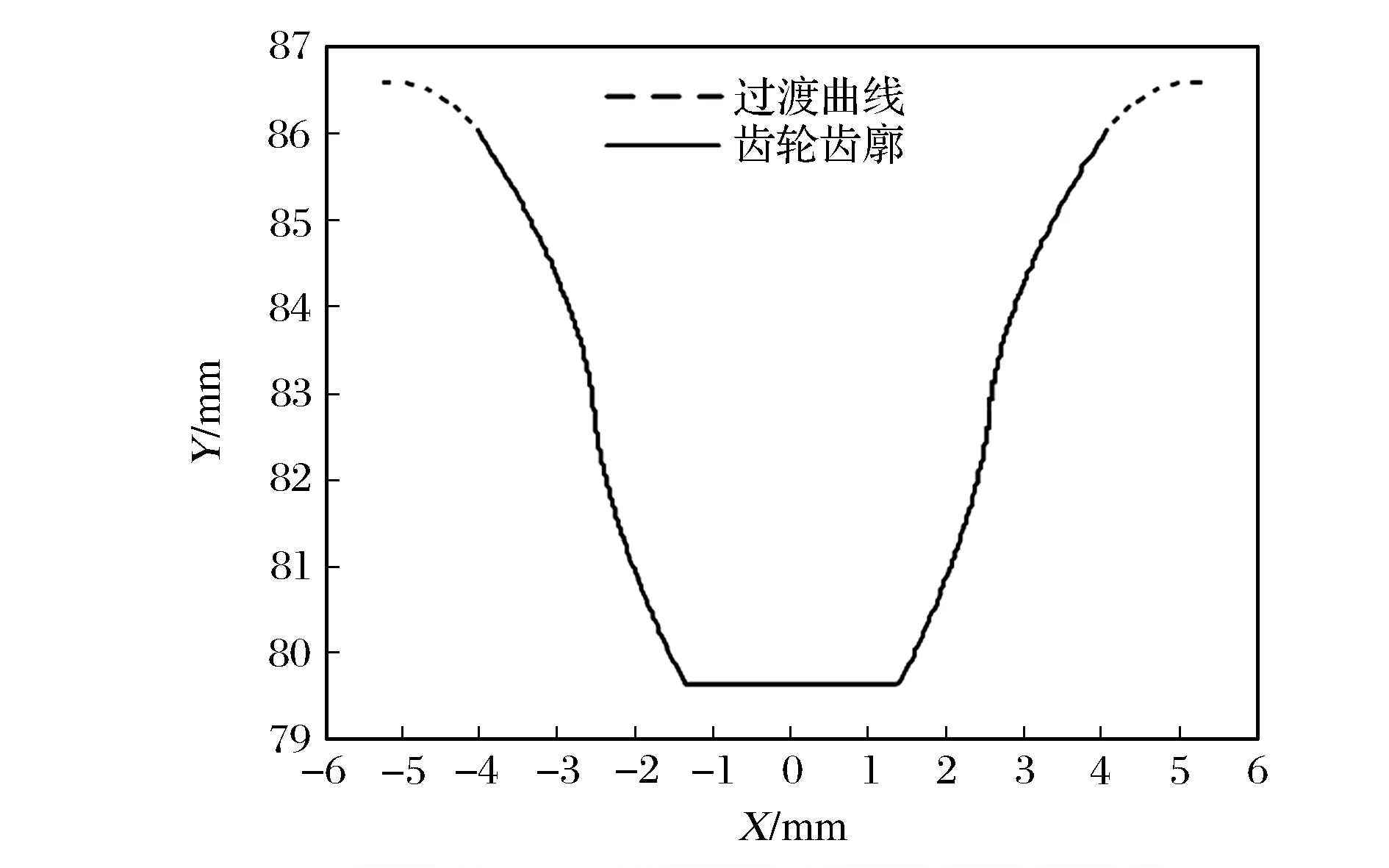
图9 摆线内齿轮的完整齿廓

4 结 语

(1)本文结合机械生产实际，对现有常用的齿轮加工方法及其过渡曲线形式进行分析得出：齿轮加工方法或刀具类型的不同，得到的齿根过渡曲线就不相同；即便采用同一加工方法和加工刀具，如刀具的齿顶形状不同，得到的过渡曲线亦不相同。

(2)选取具有代表性的加工方案，建立摆线齿轮加工刀具的齿廓模型，根据齿轮啮合理论，推导了用以典型形状为齿顶的常用范成刀具加工摆线齿轮时生成过渡曲线的方程，并由程序进行验证。

(3)精确的齿根过渡曲线对于齿轮弯曲强度的评价具有重要意义，建立过渡曲线精准数学模型和由Matlab软件编写的计算程序，为提高齿轮结构设计和强度分析的准确性奠定基础。

[1] Φ． Л 李特文 ．齿轮啮合原理[M]．卢贤占、高业田、王树人，译．2版．上海：上海科学技术出版社，1984：210．

[2] 余以道，王建，罗善明，等．新型余弦齿轮传动的重合度分析[J]．湖南科技大学学报(自然科学版)，2007，22(1)：38-41．

[3] 赵韩，吴其林，黄康，等．国内齿轮研究现状及问题研究[J]．机械工程学报，2013，49(19)：11-20．

[4] 李杰，张磊，赵旗．常见齿轮过渡曲线对应齿轮弯曲应力的比较分析[J]．机械传动，2008，32(6)：101-103．

[5] 王健力，毕合春，刘奎丰．滚齿加工的齿轮齿根过渡曲线[J]．机械传动，2013，37(1)：82-86．

[6] 于杰，王宝雨．一种齿根过渡曲线的求解方法[J]．机械设计与制造，2012(3)：190-192．

[7] 朱景梓，张展，秦立高．渐开线外啮合圆柱齿轮传动[M]．北京：国防工业出版社，1990：105．

[8] 吴继泽，王统．齿根过渡曲线与齿根应力[M]．北京：国防工业出版社，1989：10-11．

(编辑：史海英)

RootFilletCurveofInternalCycloidGearBasedonGeneratingMethod

GUI Xincheng1, LI Hongxun2, LI Lishun2, NIU Sibo3
(1.Postgraduate Training Brigade, Army Military Transportation University, Tianjin 300161, China; 2.National Emergency Transportation Equipment Engineering Technology Research Center, Army Military Transportation University, Tianjin 300161, China; 3.Unit 68117, Lanzhou 730070, China)

● 基础科学与技术BasicScience&Technology

10．16807/j.cnki.12-1372/e.2017.09.021

TH132.414

A

1674-2192(2017)09- 0091- 05

2017-03-20；

2017-04-15．

贵新成(1990—)，男，博士研究生．