航天器远程自主交会方法设计与实现
2017-10-13马晓兵
李 蒙,马晓兵,2
(1. 中国空间技术研究院载人航天总体部,北京 100094;2. 南京航空航天大学航空宇航学院,南京 210016)
航天器远程自主交会方法设计与实现
李 蒙1,马晓兵1,2
(1. 中国空间技术研究院载人航天总体部,北京 100094;2. 南京航空航天大学航空宇航学院,南京 210016)
为解决未来交会对接任务的自主化问题,提出航天器远程自主交会方法。给出适用于远程自主交会的变轨策略,设计航天器上自主变轨规划算法,通过初值计算和精确解迭代两个步骤对变轨策略进行求解,获得变轨控制参数。采用拟平均根数法结合平均密度法进行轨道预报,在尽量保证模型精度的同时极大降低了轨控参数求解过程中的在轨计算量。仿真结果表明,使用该方法规划的远程导引段轨道控制,可使终端精度满足指标要求,且方法简单可靠、合理可行,具有工程应用价值。
航天器;远程;自主变轨规划;解析法轨道预报
0 引 言
航天器交会对接(Rendezvous and docking,RVD)技术是航天工程中的一项关键技术,是实现空间站、空间平台和空间运输系统空间装配、回收、补给、维修及营救等在轨服务,以及载人登月、外星采样和星际航行任务的基石[1-3]。迄今为止,世界上已经开展过200多次空间交会对接,其中绝大多数由美国和苏联(俄罗斯)完成。我国于2011年至2016年间分别进行了神舟八号、神舟九号、神舟十号与天宫一号、神舟十一号与天宫二号的自动和手动交会对接,标志着我国载人航天工程已经突破并掌握了交会对接技术,即将全面进入空间站任务阶段[4]。
交会对接任务按照飞行过程一般分为远程导引段、近程导引段、平移靠拢段和对接段。远程导引段从追踪飞行器入轨开始至器上敏感器捕获目标为止,导引终端两飞行器间距离为一百千米至几十千米。远程导引段主要由地面进行测定轨和机动计算,追踪飞行器根据地面上注的控制参数实施变轨,最终在预定的时刻获得期望的状态[5]。未来任务对交会对接策略提出了新的需求[6]:一方面,由于任务时效性约束,要求交会对接时间尽可能短。2012年起俄罗斯成功实施了联盟号飞船与国际空间站的若干次快速交会对接,飞船从入轨到对接仅需6小时[7]。另一方面,未来空间站运营和维护使发射密度增加,天地往返飞行日益频繁,地面飞行控制人力和物力资源占有量持续增加。综上,传统意义上通过地面测定轨、计算控制参数、校核注入数据等复杂流程完成远程导引的模式已经不能满足新任务需求。为了缩短远程导引时间,简化航天器的地面支持系统,减少操作的复杂性,降低任务的费用,必须采用不依赖于地面的航天器在轨自主化远程交会技术。
实现航天器远程自主交会的核心是合理可行的自主轨道预报算法和自主变轨规划算法,在达到任务精度要求的同时,计算量小,便于在轨自主实时运算。目前,针对远程导引变轨策略的理论研究,由于没有考虑轨道摄动以及实际约束,研究结果与实际轨道将具有较大差异,但其基本方法及获得的一些重要结论对实际轨道设计具有重要的参考意义。工程研究中,国际上广泛应用的远程导引变轨规划方法包括俄罗斯联盟号、进步号飞船采用的综合变轨策略[8],以及美国航天飞机、龙飞船采用的特殊点变轨策略[9]。特殊点变轨的轨道机动位置一般选择在远地点、近地点和升交点等特殊点,进行轨道面内变轨时追踪航天器无需姿态调整,且推进剂最优性可由接近Hohmann变轨的变轨方案保证,但由于只有五个设计变量不能直接瞄准终端相对位置和速度[1]。综合变轨策略的变轨点不局限于特殊点,变轨冲量同时含有轨道面内外分量,每次变轨时均需调整航天器姿态,控制相对复杂,且策略求解时涉及两层非线性优化,计算量大[10]。自主交会研究中,文献[11]提出了一种基于C-W方程的改进自主交会制导算法,但该方法仅降低了由于线性化导致的模型误差,无法实现闭环控制,不能消除变轨过程引入的测定轨误差、轨控误差。文献[12]以经典轨道要素作为轨控参数,基于特殊点变轨设计了自主接近流程,但变轨次数过多,且终端只瞄准了相对位置,未对相对速度进行直接控制。文献[13]基于我国现有2天交会对接方案,从分析角度对实施快速交会对接的变轨方案与规划模型进行了研究,给出了测定轨精度需求和最优相位角范围,但未给出实施自主交会的解决方案。
本文基于未来交会对接任务需求,提出了一种实现远程自主交会的解决方案。采用基于修正特殊点变轨的实时规划变轨策略,持续修正变轨过程引入的各项误差,保证终端相对位置、速度均满足指标要求。变轨规划求解过程中,使用解析法进行轨道预报,降低了在轨计算量。
1 远程导引段变轨方案设计
1.1变轨策略
本文采用修正特殊点变轨策略,将第4次变轨点位置放开,获得6个设计变量。具有特殊点变轨姿态调整少及方案近似Hohmann变轨的特点,同时还能直接瞄准终端相对位置和速度。变轨策略如表1所示。

表1 远距离导引段变轨策略Table 1 Maneuver strategy in phasing stage
1.2变轨任务规划模型
由于测定轨误差、轨控误差、火箭入轨误差、空间环境误差等影响,航天器的实际飞行轨道并非标称设计轨道,而是与之存在一定偏离的偏差轨道。为消除或降低误差对远程导引终端的影响,使实际飞行接近标称轨道,在每次轨控前,需要重新进行测定轨和变轨序列计算[1],本文即采用这一实时规划方案。
1) 规划方案。由表2给出的实时规划方案可知,每次变轨均计算本次及后续轨控参数,因此均可瞄准终端约束目标,提高了终端精度。随着变轨的进行,可用于规划的设计变量逐渐减少,因此瞄准的终端约束目标由第1次变轨时的6个逐渐减少至第5次变轨时的1个。

表2 实时规划方案Table 2 Real-time maneuver plan
2) 终端条件。远程导引段终端时刻要求追踪航天器相对目标航天器具有一定的位置和速度,如式(1)所示。这一条件由近程导引段的轨道约束及转近程导引时的相对测量敏感器的视场角范围等性能决定。
(1)
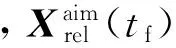
2 自主变轨规划算法
2.1近圆轨道相对运动
对于近地轨道交会对接任务,追踪航天器及目标航天器运行轨道均为近圆轨道,可认为其运动在某一理想的圆轨道附近,此时航天器的运动可用其运动与理想圆轨道运动之间的偏差描述,通常采用近圆偏差线性方程描述这一相对运动关系。
假设参考圆轨道以半径r0及角速度ω0运动,将追踪航天器及理想参考圆轨道的动力学方程建立在轨道柱坐标系中,相减并忽略高阶小量后可得航天器相对于参考圆轨道的近圆偏差线性方程[1,14]
(2)
式中:Δr、Δvr、Δar分别表示径向位置偏差、速度偏差和加速度偏差,Δθ、Δvt、Δat分别表示纬度幅角偏差、迹向速度偏差和加速度偏差,Δz、Δvz、Δaz分别表示法向位置偏差、速度偏差和加速度偏差。
在近程导引段(或称自主控制段),由于追踪航天器及目标航天器相对距离同轨道半径相比为小量,二者相对运动模型可简化为一组常系数微分方程,即C-W方程。而在远程导引段,上述假设不成立,因此C-W方程不再适用。在近圆偏差线性方程推导过程中,并未要求纬度俯角偏差Δθ为小量,所以该方程仍然适用于远程导引段。
构造状态变量X=[Δr,r0Δθ, Δz, Δvr, Δvt, Δvz]T,则可将式(2)表示为:

(3)
式(3)的解可表示为

(4)
式(3)~(4)中A、B、U、Φ、Φv的定义详见文献[14]。
当推力等效为脉冲时(作用时刻为t1,…,tn),令:
(5)
则式(4)可写为如下形式:
ΔX=FΔV
(6)
式中:ΔX为终端需要修正的偏差,ΔV为轨控速度增量。将追踪飞行器与目标飞行器轨道外推至终端时刻,根据偏差求解式(6)即可获得变轨控制参数。
2.2求解算法
1) 初值计算
根据实时规划的特点,只需计算第1次规划对应的变轨控制参数(即设计变量)初值,第1次规划的精确解可作为后续规划的初值。对于面内交会问题,设计变量为x1a=[Δvt1, Δvt 3,φ4, Δvt 4]T,根据式(6)有
(7)
式中:Δθi=2π(Nf-Ni)+(φf-φi)为第i次变轨点至远程导引终端的角度,由于第1、3次变轨点位置为确定值,则Δθ1和Δθ3确定,δvr f、δvt f、δrf、δθf分别为终端待修正的径向速度、迹向速度、径向位置、纬度幅角偏差。根据式(7)可求解出x1a。
对于面外问题,设计变量取为x1b=[φ2, Δvz 2]T,根据式(6)有
(8)
式(8)的解析解为
(9)

(10)
Δθ2所在象限以及Δvz 2的符号由表1中第2次变轨的纬度幅角范围确定。
2) 精确解迭代
以上部分给出了设计变量的初值计算方法,下面给出如何根据初值进行迭代获得摄动条件下精确满足终端条件的变轨序列。
考虑在轨计算能力限制,采用简单易行的牛顿迭代法进行精确求解。构造非线性方程组h如下:
(11)

hi(x1,x2,…,xn)=0,i=1,2,…,n
(12)
式(12)的求解公式为
xk+1=xk-[H(xk)]-1h(xk)
(13)
式(13)中上标k为迭代次数,H(x)为雅克比矩阵:
(14)
每次迭代对应的H(xk)可采用数值差分方法进行计算。当式(11)满足一定的收敛条件时即可停止迭代,从而得到设计变量x的精确解。
3 自主轨道预报算法
3.1基本变量选择
追踪飞行器在轨规划变轨控制参数时,需要将轨道预报至远程导引终端,并计算终端状态。由于在轨计算能力限制,不能采用通常情况下地面使用的高精度轨道摄动方程数值积分的方法进行轨道外推。考虑这一约束,采用解析法外推轨道。
由于目前研究的交会对接多在近地轨道完成,对应偏心率较小,使用解析法进行轨道外推时可能出现奇点,为避免这一现象,轨道外推适宜使用拟平均根数法[15]。根据开普勒轨道根数构造第一类无奇点变量如下:

(15)
式中:a为归一化后的轨道半长轴(将轨道半长轴与地球参考椭球体赤道半径相除),i为轨道倾角,Ω为升交点赤经,e为偏心率,ω为近地点幅角,M为平近点角。
3.2摄动解的具体表达形式
对于地球非球型引力摄动(考虑到J2带谐项系数),采用拟平均根数法,无奇点摄动解表示为
(16)
在一阶意义下,形式为:
(17)

考虑到整个系统软硬件的状况和人员配置问题,备用系统的运行维护采用如下方式:数据服务器、前置服务器、历史服务器长期带电运行,任何时候保证两个系统的图形和数据库的同步。其他设备如调度员工作站定期半个月进行一次通电试运行,对各项功能进行测试,如果发现问题,马上处理。这样的运行维护方式可以减少调度自动化人员的工作量,又能保证备用系统随时可以投人运行。
无奇点变量的一阶长期项表达式为:
(18)
(19)
(20)
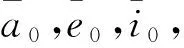

3.3大气阻力摄动
对于低轨航天器,大气阻力是影响轨道预报精度的主要摄动因素,必须加以考虑。这里采用平均密度模型构造大气阻力摄动解。
平均密度模型利用给定参考点的平均大气密度表,通过指数模型和周日模型计算当前时刻当前高度的大气密度。假设参考点高度为r0,对应的平均密度和标高分别为ρ0和H0,则当前时刻的大气密度为[16]:
(21)
式中:r为当前时刻航天器高度,H为当前高度的标高,这一数值可用H=H0+ 0.1(r-r0)计算,φ为当前时刻航天器与周日密度峰的夹角,密度峰一般落后太阳2~3 h,即30°~45°,F*表示周日周期振幅,即
(22)
式中:f*表示周日密度最大值与最小值之比。
(23)
式中:CD为大气阻力系数,S/m是卫星面质比,V和V分别为卫星相对大气的速度矢量和模值。
将大气阻力摄动加速度代入摄动方程中,经过数学变换,即可得到阻力摄动影响,通常只需要给出阻力摄动的二阶长期项σ2。半长轴a2和λ2阻力摄动的二阶长期项具体表达式如下:
(24)其中,A=CDS/m,I(z)为贝塞尔函数,k由下式表示:
(25)
将大气阻力摄动作为二阶长期项代入式(17)第1式后即得到考虑地球非球型引力及大气阻力的轨道外推解析表达式。
4 算例分析
4.1仿真校验流程
为校验自主交会算法的正确性及精度,将STK高精度轨道预报模块作为“真实”任务环境,设计如下仿真校验流程,如图1所示。
1)利用STK将初始轨道外推至第1次变轨前,并施加定轨误差。
2)根据含定轨误差的轨道数据,使用本文提出的自主交会算法进行第1次变轨控制参数规划。
3)将轨控参数代入STK,模拟真实变轨过程并外推至下一次轨控前,获取控后轨道数据,施加定轨误差。
4)使用本文提出的算法进行新一次变轨控制参数规划,并返回步骤3直至第5次变轨。
5)将第5次变轨的轨控参数代入STK外推至终端,考核终端误差。
4.2计算条件
追踪飞行器入轨时刻(UTCG时间)为2020年1月1日12时0分0秒,初始时刻t0=0 s,终端时刻tf=149475 s,初始圈次1。

图1 仿真校验流程Fig.1 Process of simulation
初始轨道要素(a,e,i,Ω,ω,f):目标器Etar(t0)= (6764 km,0.0006,42.7781°,9.06413°,0°,209°);追踪器Echa(t0) = (6661 km,0.01351,42.778°,9.06913°,125.326°,359.82°)。变轨圈次为N1=4,N2=13,N3=20,N4=23,N5=26。
为模拟真实任务环境,STK中设置仿真参数如下:引力场为32×32阶的WGS84模型,考虑太阳及月球的三体摄动,大气模型采用NRLMSIS- 00,阻力系数CD=2.2,太阳10.7 cm辐射通量F10.7 =130.6,地磁指数Ap=13。目标器质量8300 kg,阻力面积30 m2;追踪器质量8100 kg,阻力面积20 m2。
远程导引终端,目标航天器坐标系中期望的追踪航天器状态按径向、迹向和法向的相对位置和速度给出:(-14 km,-40 km,0 km,0 m/s,24 m/s,0 m/s)。以上各元素允许的偏差指标为:(±2 km,±8 km,±1 km,±1 m/s,5 m/s,±1 m/s)。
4.3计算结果
1)标称轨道仿真
将图1中定轨误差设置为零,使用自主交会算法获得的远程导引轨控参数如表3所示。

表3 远程导引轨控参数Table 3 Control parameters of phasing stage
STK计算获得的远程导引终端条件为:(-14.0673 km,-40.0367 km,0.0613 km,0.0086 m/s,24.1941 m/s,0.0224 m/s)。与期望状态的偏差为(-0.0673 km,-0.0367 km,0.0613 km,0.0086 m/s,0.1941 m/s,0.0224 m/s)。这一结果表明,本文提出的方法产生的终端偏差远小于第4.2节中的指标要求。
需要说明的是,上述终端偏差完全是由于简化的轨道预报解析模型与高精度数值模型之间的差异导致的。虽然受在轨计算能力限制,只能采用解析法进行轨道预报,但由于使用了实时规划的变轨策略,在轨不断修正模型误差,最终可将终端偏差控制在很小的范围内。
图2和图3分别为远程导引段追踪飞行器半长轴变化曲线和相位差变化曲线。

图2 半长轴变化曲线Fig.2 Semi-major axis vs. time

图3 相位差变化曲线Fig.3 Phase difference vs. time
2)偏差轨道仿真
为考核偏差情况下的远程导引终端精度,考虑定轨误差,进行偏差轨道仿真。
定轨误差按如下指标设置:(±10,±1×10-4,±1.5×10-3,±1.5×10-3,±1,±2×10-3)。误差元素定义分别为:半长轴(m),偏心率,轨道倾角(°),升交点赤经(°),近地点幅角(°),纬度幅角(°)。
定轨误差中的每个元素取正负极值组合,分别施加在各次定轨环节中,如图1所示。为满足最大包络要求,追踪飞行器的定轨误差与目标飞行器的定轨误差符号取反。因此,可得考虑定轨误差后的偏差仿真工况为26=64组。
按照上述条件进行偏差仿真后,得到的相对位置和速度最大偏差包络如下:(±0.392 km,±2.195 km,±0.471 km,±0.376 m/s,±0.966 m/s,±0.469 m/s)。这一结果表明,在考虑定轨误差情况下,本方法产生的远程导引终端偏差仍然满足指标要求。
5 结 论
本文提出了一种航天器远程自主交会方法。在给定的初始条件下,通过求解相对运动方程获得轨控参数的初始解,在此基础上利用牛顿迭代法获得摄动条件下满足终端要求的精确解。由于求解过程使用解析法进行轨道外推,降低了在轨计算量。将求解得到的轨控参数代入高精度模型中进行仿真校验,结果表明,考虑定轨误差后远程导引终端相对位置速度均满足指标要求。因此,本文给出的方法合理可行,具有工程应用价值。
[1] 张柏楠. 航天器交会对接任务分析与设计[M].北京:科学出版社, 2011:1-47.
[2] 吴宏鑫, 胡海霞, 解永春, 等.自主交会对接若干问题[J]. 宇航学报, 2003, 24(2): 132-137. [Wu Hong-xin, Hu Hai-xia, Xie Yong-chun, et al. Several questions on autonomous rendezvous docking [J]. Journal of Astronautics, 2003, 24(2): 132-137.]
[3] 刘伟杰, 谌颖.航天器椭圆轨道自主交会的鲁棒H∞控制[J]. 宇航学报, 2015, 36(2): 179-185. [Liu Wei-jie, Chen Ying. Robust H∞control for autonomous elliptic orbit rendezvous of spacecrafts [J]. Journal of Astronautics, 2015, 36(2): 179-185.]
[4] 张柏楠, 马晓兵, 郑伟, 等.中国载人交会对接技术的设计与实现[J]. 中国科学:技术科学, 2014, 44(1): 1-11. [Zhang Bai-nan, Ma Xiao-bing, Zheng Wei, et al. Design and implementation of China’s manned rendezvous and docking technology [J]. Scientia Sinica Technologica, 2014, 44(1): 1-11.]
[5] 王为, 王翔, 龚胜平.一种基于CW方程的交会远程导引终端误差分析新方法[J]. 宇航学报, 2016, 37(2): 189-194. [Wang Wei, Wang Xiang, Gong Shen-ping. A new method for rendezvous remote guidance terminal error analysis based on CW equation [J]. Journal of Astronautics, 2016, 37(2): 189-194.]
[6] 周建平. 我国空间站工程总体构想[J].载人航天, 2013, 19(2): 1-10. [Zhou Jian-ping. Chinese space station project overall vision [J]. Manned Spaceflight, 2013, 19(2): 1-10.]
[7] Murtazin R F, Budylov S G. Short rendezvous missions for advanced Russian human spacecraft [J]. Acta Astronautica, 2010, 67(7-8): 900-909.
[8] Baranov A A. Algorithm for calculating the parameters of four-impulse transitions between close almost-circular orbits [J]. Cosmic Research, 1990, 24(3): 324-327.
[9] Young K A, Alexander J D. Apollo lunar rendezvous [J]. Journal of Spacecraft and Rockets, 1970, 7(9): 1083-1086.
[10] 罗亚中, 唐国金. 两层非线性规划问题的并行模拟退火全局优化[J]. 系统仿真学报, 2005, 17(5): 1040-1044. [Luo Ya-zhong, Tang Guo-jin. Global optimization of bilevel nonlinear programming problems by parallel simulated annealing [J]. Journal of System Simulation, 2005, 17(5): 1040-1044.]
[11] 程博, 荆武兴, 陈伟跃. 远程自主交会改进制导算法[J]. 宇航学报, 2008, 29(6): 1804-1813. [Cheng Bo, Jing Wu-xing, Chen Wei-yue. Improved guidance algorithm for remote autonomous rendezvous [J]. Journal of Astronautics, 2008, 29(6): 1804-1813.]
[12] 赵书阁, 陈统, 徐世杰. 航天器交会远程快速自主制导方法[J]. 北京航空航天大学学报, 2012, 38(12): 1582-1586. [Zhao Shu-ge, Chen Tong, Xu Shi-jie. Fast autonomous guidance algorithm for spacecraft far range rendezvous phasing [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(12): 1582-1586.]
[13] 杨震, 罗亚中, 张进. 近地快速交会调相策略设计与任务分析[J]. 国防科学技术大学学报, 2015, 37(3): 61-67. [Yang Zhen, Luo Ya-zhong, Zhang Jin. Analysis and design of phasing strategy for near-earth short rendezvous mission [J]. Journal of National University of Defense Technology, 2015, 37(3): 61-67.]
[14] 张进. 空间交会远程导引变轨任务规划[D]. 长沙: 国防科学技术大学, 2008. [Zhang Jin. Orbital maneuver planning for rendezvous at phasing stage [D]. Changsha: National University of Defense Technology, 2008.]
[15] 刘林, 汤靖师. 卫星轨道理论与应用[M]. 北京:电子工业出版社, 2015:195-227.
[16] 汤靖师, 刘林. 低轨航天器长期轨道预报的初步研究[J]. 飞行器测控学报, 2014, 33(1): 59-64. [Tang Jing-shi, Liu Lin. On long-term orbit prediction for low earth orbit spacecraft [J]. Journal of Spacecraft TT & C Technology, 2014, 33(1): 59-64.]
DevelopmentofLongDistanceAutonomousRendezvousforSpacecraft
LI Meng1, MA Xiao-bing1,2
(1. Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China;2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
In order to realize automatization in rendezvous and docking mission, a method of long distance autonomous rendezvous for spacecraft is proposed. A maneuver strategy adapted to long distance autonomous rendezvous is designed. The control parameters are obtained by the autonomous maneuver plan algorithm which contains the initial value calculating and accurate solution iterating. The quasi-mean element method combined with the mean atmosphere density method is used to reduce the on-orbit calculation quantity. The simulation result shows that the design variables of this method satisfy the terminal conditions well.
Spacecraft; Long distance; Autonomous rendezvous; Analytic orbit prediction
V412.4
A
1000-1328(2017)09-0911-07
10.3873/j.issn.1000-1328.2017.09.003
2017- 03-13;
2017- 07- 02
李蒙(1984-),男,博士,高级工程师,主要从事载人航天器总体设计、交会对接轨道设计。
通信地址:北京5142信箱340分箱(100094)
电话:(010)68745499
E-mail: Arahms@sina.com
