面向相似App推荐的列表式多核相似性学习算法①

卜 宁, 牛树梓, 马文静, 龙国平



面向相似App推荐的列表式多核相似性学习算法①

卜 宁, 牛树梓, 马文静, 龙国平

(中国科学院软件研究所, 北京 100190)

相似App推荐可以有效帮助用户发现其所感兴趣的App. 与以往的相似性学习不同, 相似App推荐场景主要面向的是排序问题. 本文主要研究在排序场景下如何学习相似性函数. 已有的工作仅关注绝对相似性或基于三元组的相似性. 本文建模了列表式的相似性, 并将三元组相似性与列表式相似性用统一的面向排序场景的相对相似性学习框架来描述, 提出了基于列表的多核相似性学习算法SimListMKL. 实验证明, 该算法在真实的相似App推荐场景下性能优于已有的基于三元组相似性学习算法.

相似App推荐; 多核学习; 相对相似性; 相似性学习; 列表式学习

智能手机和移动互联网的广泛普及, 带动了移动应用(Mobile Application, 简称App)的飞速发展, 越来越多的用户每天都要使用移动App, 但是用户发现找到自己感兴趣的App越来越困难. 相似App推荐可以有效缓解这个问题. 例如, Google Play应用商店在每个App的详情页面提供与该App相似的App列表. 然而, 如何定义两个App之间的相似程度成为相似App推荐中的关键问题.

移动App本质是一个应用程序, 但实际上公开可获得的只是其基本情况描述信息, 本文中称为App的元信息. 这些元信息通常存在于移动App商店中, 包括名称, 功能描述, 屏幕截图, 用户评论, 开发商, 用户评分, 大小等信息. 因此本文所关注的移动App的本质是一个异质信息的聚合体. App相似性学习可以转换为多元异质信息间的相似性学习.

已有的相似性学习算法可以分为基于特征的学习算法与基于核函数的学习算法. 前者侧重于多元异质信息的表示学习, 后者更侧重于如何融合多个异质的核函数. 本文采用主流的基于多元核函数的方法来学习App相似性, 优势在于便于针对不同的信息采用合适的核函数, 有效的规避了信息间的异质性问题. 在面向排序的的相似性学习场景中, 给定目标对象a, 我们需要一个按与a相似程度, 从由高到低排序的列表, 而非与其中某个对象相似程度的一个具体值, 例如相似App推荐. 相似App列表整体质量的好坏是核心. 已有一些工作[1,2]关注于三元组形式的相对相似性, 如(a,b,c)描述了对于对象a来说, b比c更相似. 基于三元组的相似性学习算法将相似性学习的问题归约为对于对象a, 对象b是否比c更相似的分类问题, 试图优化分类错误. 这样做只考虑了局部序的损失, 与我们所关心的排序列表的整体质量不一致, 因此本文提出直接建模排序列表(Listwise)质量, 将其作为优化目标, 来学习App相似性, 称为SimListMKL. 在真实数据集上的实验结果表明, 本文提出的SimListMKL算法要优于主流的基于三元组的相对相似性学习算法.

1 相关工作

相似性学习是一种有监督的学习方式, 它从已有的相似关系的对象中学习相似性函数, 度量两个对象的相似程度[1]. 相似性学习所面向的任务有回归, 分类与排序等. 本文主要关注面向排序场景的相似性学习. 基于特征的方法在于学习一个特征映射函数, 然后根据该映射定义相似性函数. 基于核函数的方法包括单核函数的方法与多核函数方法, 其中单核函数方法与基于特征的方法类似, 多核函数方法一般要优于单核方法, 但计算代价高. 因此本文主要从基于特征的方法(单核方法)与基于多核函数的方法两方面阐述.

已有的基于特征的相似性学习的方法直接从成对的相似关系约束中学习相似性函数. 这些工作假设相似性度量的应用场景为回归或分类, 因此大多将相似性学习的问题归约为分类问题. 文献[3]将脸部识别问题归约为差分空间中的相似性判别二分类问题, 并采用SVM求解. 相似性神经网络[5](Similarity Neural Network)提出采用前向多层感知机来学习一个非负且对称的相似性度量, 其中非负性由输出层的sigmoid激活函数保证, 对称性由网络结构的权重共享机制决定. 文献[6]将相似性度量学习的问题转化为对象的特征权重的学习问题, 优化目标是经过特征权重的线性变换使得相似的两个对象距离尽可能小, 并约束不相似的两个对象间的距离尽量大. 成对相似性关系大多是一种绝对的表示, 但是相对的相似性关系的比较是表达领域知识的更为自然的方式, 因为相似性的知识通常是模糊的, 只有相对意义上的表示. 对象a与对象b相似度比对象c与对象d之间的更高, 这一点很容易确定. 对于对象a与对象b之间是否相似给一个绝对的值要困难一些. 有些基于特征的相似性学习方法关注从这种相对的相似性关系中学习相似性函数. 文献[7]考虑了将相对相似性约束应用到聚类问题中所面临的可行性, 完备性以及信息量. 文献[8]建模了这种相对相似性的领域知识, 将关于相对相似性的约束的均方残差作为优化目标, 有效改善了聚类准确率.

基于多核函数的方法是目前解决该问题的主流方法. 基于多核函数的相似性学习通过对多个核函数进行综合获得最优的描述相似性的核函数[9,10]. 文献[11]将学习多个核函数的组合权重的问题简化为分类问题, 采用类似于AdaBoost的方法求解. 考虑到相似度量的非负性, 文献[12]将成对对象作为训练实例, 这样每一个训练实例都用若干核函数来描述, 采用epsilon不敏感回归函数作为优化目标, 找到核函数的最优组合. 面向排序场景的多核函数方法大将相对相似性的比较作为监督信息来学习多个核函数的权重[1,2]. 考虑多核方法的计算代价高, SimApp[1]与OASIS[2]均建模hinge损失函数, 前者采用在线梯度下降的优化算法得到核函数权重称为在线核函数权重学习(OKWL)方法, 后者采用在线的Passive-Aggressive算法求解.

2 面向排序的相似性学习框架

本文首先给出App相似性问题的形式化定义, 接下来基于多核学习思想, 提出了面向排序的相似性学习框架, 最后给出了具体实例.

2.1 App相似性学习问题形式化

描述App的元信息包括多种类型, 如名称, 功能描述等为文本信息, 屏幕截图为图像信息, 用户评分为数值信息等. App间的语义相似性直接由描述App的文本间, 图像间以及文本与图像间的语义相似性等决定. 因此本文将App相似性形式化为问题1.

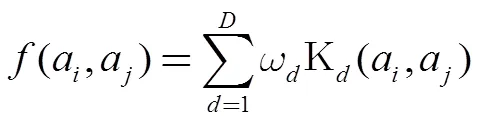
2.2 面向排序的相似性学习框架

传统的相似性学习问题认为相似性是绝对的, 例如a与b相似记为1, 不相似记为0, 因此采用分类或回归算法求解相似性学习的问题. 在排序场景下, 相对相似性比绝对相似性要重要. 例如, 相似App推荐只需关心前个App比个之后的App相比, 与当前App更相似即可, 而不需要确定具体的相似性分值是1还是0.

无论是绝对相似性标注, 还是相对相似性标注, 采用相对相似性的形式进行组织训练实例, 由此定义损失函数如公式(2)所示, 来学习App相似性函数中的核函数权重. 这就是面向排序的相似性学习框架. 以下是两个具体的实例来说明相对相似性在损失函数中的建模.

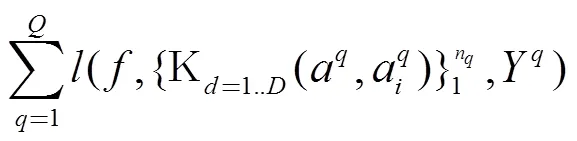
2.3 基于三元组的相似性学习算法

本文以排序学习[13]中最常见的三类建模成对实例的方式来定义损失函数. 以一个查询App的损失函数的定义为例来说明. 将代表与关系的D维核函数特征记为, 因此损失函数表示为.

①基于交叉熵的损失函数SimTripletNet

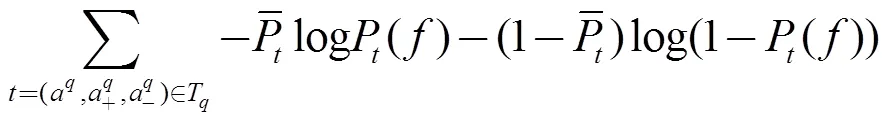
②基于指数函数的损失函数SimTripletBoost

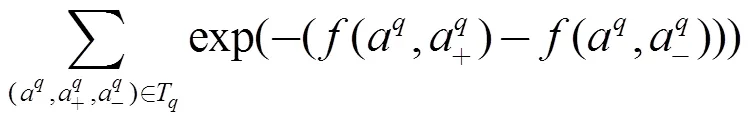
③基于Hinge损失函数SimTripletSVM

(5)

已有的工作大多是采用的Hinge损失来从三元组中学习相对相似性[1,2], 根据采用不同的优化算法得到不同的算法. 本文中将他们统一称为SimTripletSVM. 为了完备起见, 本文引入了其他可能的基于三元组的损失函数定义方式作为对比.

2.4 基于列表的相似性学习算法

中国汽车维修行业协会原会长康文仲，交通运输部科学院原党委书记、中国汽车保修设备行业协会原副会长王晓曼，中国汽车维修行业协会原会长孙守仁，中国汽车保修设备行业协会原副会长罗大柱 ，中国汽车保修设备行业协会原副会长张熙伦，中国汽车保修设备行业协会原副会长兼秘书长田国华，中国汽车维修行业协会常务副秘书长王逢铃， 中国汽车保修设备行业协会原常务副秘书长刘蕴，中国汽车保修设备行业协会秘书长刘建农，中国汽车维修行业协会连锁工委秘书长严雪月，广东省道协机动车维修检测分会会长罗少泽，北京汽车维修行业协会副秘书长侯金凤及数十位国内知名汽保企业负责人作为嘉宾出席此次茶话。

基于三元组的相似性学习算法建模了三元组这样的局部序, 所带来的损失, 没有考虑排序列表整体的质量. 基于三元组的算法将整个相似性列表拆分为三元组的形式, 将每个三元组作为一个训练实例, 强制性的认为这些三元组服从独立同分布假设. 本文将整个排序列表视为一个训练实例, 采用基于位置的评价指标作为排序列表质量的度量, 将其作为优化目标, 采用LambdaMART定义损失函数的方式, 如公式(6)所示.

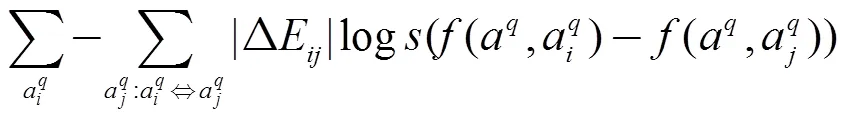
3 SimListMKL算法

本文采用SimListMKL算法来优化公式(6)所示的优化目标, 评价指标采用MAP, 为基于所有查询App的AP(Average Precision)的平均. 因此这里的MAP的变化应该对应到AP的变化. 公式(7)给出了对于一个查询App在已知其二值标注Y的情况下, 计算模型f产生的预测序的AP值.

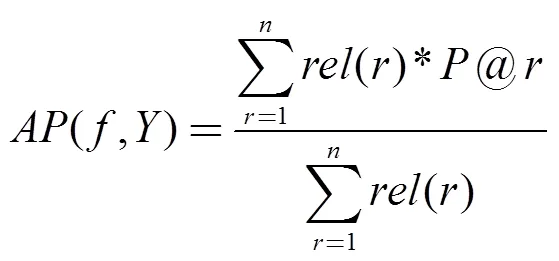
(8)

SimListMKL算法采用MART来优化目标函数公式(6). MART是一类Boosting算法, 可以视为泛函空间的梯度下降算法.

SimListMKL算法 Input: the number of trees N; The number of leaves per tree L; Learning rate ; training samples Output: 1For do 2 For do 3 4 end 5end 6For t = 1 to N do 7 For q = 1 to Q do 8 For do 9 10 11 end 12 end 13 Obtain a L leaf tree from 14 Denoted as , where each leaf value 15 is 16 17end

如算法SimListMKL所示, 第1~5行描述了模型的初始化过程, 第6~17行描述了每一个迭代步生成一个用来公式(6)中损失函数的梯度的回归树, 该树具有L个叶子节点, 叶子节点的值由Newton-Raphon更新步确定. 算法最终得到的即为本文要求解的App相似性函数.

4 实验结果

为了验证SimListMKL算法的有效性, 本文首先介绍了实验设置. 接下来介绍了基于三元组相似性的多核学习算法与本文提出的基于列表相似性的多核学习算法, 在相似App推荐场景下的性能对比. 最后对比了各类算法性能受不同类型数据集的影响以及各类算法的运行时间.

4.1 实验设置

实验数据集采用的是SimApp[1]中所用的训练数据集. 该数据集来源于Google Play的真实数据, 包括约13,000个查询App, 每个查询App下约20个App, 其中相似App的比例分布如图1所示. 横轴表示相似App的比例范围, 如0.1对应的是相似App比例在0~0.1之间的查询App的比例. App之间的相似性由10个核函数来刻画, 包括名称, 类别, 描述, 开发商, 屏幕截图, 大小, 用户评分, 用户评论, 更新信息, 许可.

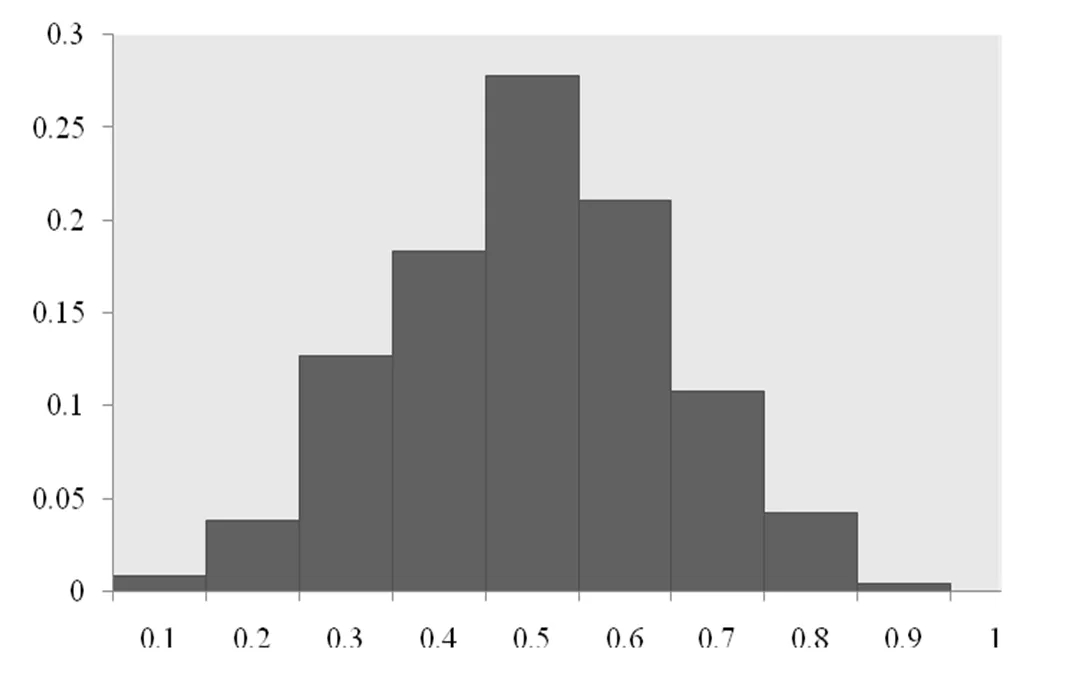
图1 相似App比例分布

本文的主要基准算法是基于三元组的相似性学习算法, 包括SimTripletNet, SimTripletBoost, SimTripletSVM.尽管采用了相同的优化目标, 可是由于优化算法不同也有许多不同的变种, 如SimTripletSVM对应的OKWL算法与OASIS算法, 这里将它们统一从优化目标的角度命名. 基于交叉熵损失函数的SimTripletNet采用梯度下降优化算法求解, 基于指数函数损失的SimTripletBoost采用boosting优化算法求解, 基于hinge损失函数的SimTripletSVM采用切平面优化算法求解.

为了便于调参, 本文将该数据划分为5份, 采用5折交叉验证, 选取最优超参数, 即最后表中与图中所展示的结果. 所有方法的最大迭代次数均设置为100次. SimTripletNet与SimListMKL中需要设置的学习步长从10-1, 10-2, 10-3, 10-4, 10-5中选取. SimTripletSVM中的C从103, 102, 10, 1, 10-1到10-5中选取. 本文提出的算法SimListMKL中的叶子数从2到20中选取. 实验采用的基于位置的评价指标是Precision@1~10, 简记为P@1~10以及MAP.

4.2 性能分析

本文将五折交叉验证的结果分别展示在表1和图2中. 表1描述了基于P@1~10的性能对比, 图2描述了MAP作为评价指标的性能对比. 基于t-test的假设检验证明以下表和图中的对比差异是显著的.

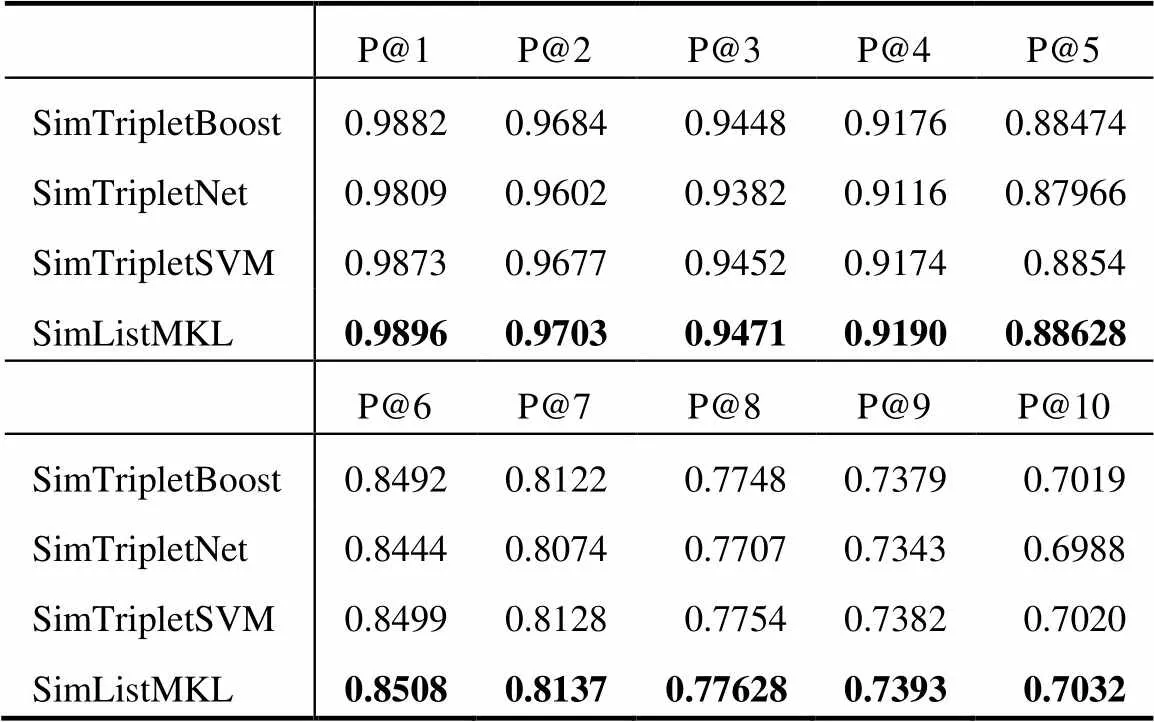
表 1 Precision性能对比

图2 MAP性能对比

表1的结果表明, 本文提出的SimListMKL方法普遍好于基于三元组的相似性学习方法. 以P@5为例, SimListMKL算法优于最好的SimTripletSVM算法约0.1%, 比最差的SimTripletNet算法约0.7%. 因此, 从Precision的度量角度来看, 基于列表建模损失函数在面向排序的相似性学习场景中是较好的选择.

图2展示的结果可以直观的表明SimListMKL算法的优势. 该算法高出SimTripletBoost约0.3%, 高出SimTripletNet约1%, 高出SimTripletSVM约0.3%. 因此, 从MAP的度量角度来看, 基于列表建模损失函数在面向排序的相似性学习场景中是较好的选择.

4.3 敏感分析

性能分析的结果显示, 算法在实验数据集上的性能普遍较好. 根据已有的排序学习算法性能受数据集影响的研究[14]表明, 这主要归因于训练数据中正负例的比例均衡.

换句话说, 即每个查询App对应的训练实例集合中, 相似App的数量占一半左右.

本实验试图打破这种均衡, 研究在不理想的数据集上算法性能的变化. ratio表示每个查询App对应的待比较App集合中相似App的数量比例. 按这个比例抽取查询App, 分别构建ratio小于0.1, 0.2, 0.3, 0.4, 0.5的数据集, 对比各算法在这些数据集上的性能表现, 如图3所示.

图3展示了不同算法在ratio不同的数据集上MAP的变化曲线. SimListMKL算法对数据集是最不敏感的, 其从0.1到0.5, 仅变化了4.4%. 而变化最大的SimTripletNet变化幅度为18.6%. SimTripletBoost与SimTripletSVM居中, 变化约为6.2%. 由此可以看出, SimListMKL是一个稳定的算法, 不容易受数据集好坏的影响.

4.4 运行时间分析

本部分实验对比了三元组的相似性学习算法与基于列表的相似性学习算法的训练时间. 图4展示了在Win7-64位操作系统, 4GB内存, i7-2600 CPU, 主频3.4GHZ的环境下, 两组算法分别采用五折交叉验证时, 平均每折的运行时间(单位: 秒).

由图4可得, SimTripletSVM运行时间最短约为2.8秒, 这一时间要远远好于同属于基于三元组的相似性学习算法的SimTripletBoost(约14.2秒)与SimTripletNet(约28秒)算法. SimTripletSVM算法的高效一部分原因在于采用的是C实现, 而其他所有算法都采用的是Java实现.

本文提出的算法SimListMKL运行时间约为14.2秒, 与基于三元组的相似性学习算法SimTripletBoost相当, 远远好于SimTripletNet. SimListMKL与SimTripletBoost均采用了Boosting的优化算法, 而SimTripletNet采用了梯度下降算法. 可见, 影响运行时间的因素主要取决于优化算法的具体实现. 本文提出的SimListMKL优化目标虽然复杂, 并没有给优化算法带来太多额外的时间开销.

5 结语

针对排序场景中的相似性学习问题, 本文总结出了一个基于相对序的相似性学习框架, 并提出了基于列表的多核相似性学习算法SimListMKL. 与已有的基于三元组相对相似性学习的算法相比, SimListMKL算法采用了一个更为概括的形式, 即列表的相对相似性, 并基于此建模了损失函数, 并采用MART算法优化. 实验结果表明, SimListMKL是一种更好的建模相对相似性的方式, 提升了相似App推荐的性能, 同时保证较高的时间效率. 多核相似性学习方法的显著问题是计算复杂度高, 下一步的研究工作主要是在线SimListMKL算法.

1 Chen N, Hoi S C H, Li S, et al. SimApp: A framework for detecting similar mobile applications by online kernel learning. Proc. of the 8th ACM International Conference on Web Search and Data Mining. ACM. 2015. 305–314.

2 Chechik G, Sharma V, Shalit U. Large scale online learning of image similarity through ranking. Journal of Machine Learning Research, 2010: 1109–1135.

3 https://en.wikipedia.org/wiki/Similarity_learning#cite_note-4.

4 Guo G, Li S, Chan K. Support vector machines for face recognition. Image and Vision Computing, 2001, 19(9): 631–638.

5 Melacci S, Sarti L, Maggini M, et al. A neural network approach to similarity learning. IAPR Workshop on Artificial Neural Networks in Pattern Recognition. Springer Berlin Heidelberg. 2008. 133–136.

6Xing EP, Ng AY, Jordan MI, et al. Distance metric learning with application to clustering with side-information. Advances in Neural Information Processing Systems, 2003, 15: 505–512.

7 Liu E Y, Zhang Z, Wang W. Clustering with relative constraints. Proc. of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM. 2011. 947–955.

8 Liu E Y, Guo Z, Zhang X, et al. Metric learning from relative comparisons by minimizing squared residual. 2012 IEEE 12th International Conference on Data Mining. IEEE. 2012. 978–983.

9 Lanckriet GRG, Cristianini N, Bartlett P, et al. Learning the kernel matrix with semidefinite programming. Journal of Machine Learning Research, 2004, 5(Jan): 27–72.

10 Ying Y, Zhou DX. Learnability of Gaussians with flexible variances. Journal of Machine Learning Research, 2007, 8(Feb): 249–276.

11 Tang Y, Li L, Li X. Learning similarity with multikernel method. IEEE Trans. on Systems, Man, and Cybernetics, 2011, 41(1): 131–138.

12 Chen LB, Wang YN, Hu BG. Kernel-based similarity learning. Proc. 2002 International Conference on Machine Learning and Cybernetics. IEEE. 2002, 4. 2152–2156.

13 Liu TY. Learning to rank for information retrieval. Foundations and Trends in Information Retrieval, 2009, 3(3): 225–331.

14 Niu S, Lan Y, Guo J. Which noise affects algorithm robustness for learning to rank. Information Retrieval Journal, 2015, 18(3): 215–245.

Listwise Multi-Kernel Similarity Learning Algorithm for Similar Mobile App Recommendation

BU Ning, NIU Shu-Zi, MA Wen-Jing, LONG Guo-Ping

(Institute of Software, Chinese Academy of Sciences, Beijing 100190, China)

Similar App recommendation is useful for helping users to discover their interested Apps. Different from existing similarity learning algorithms, the similar App recommendation focuses on presenting a ranking list of similar Apps for each App. In this paper, we put emphasis on how to learn a similarity function in a ranking scenario. Previous studies model the relative similarity in the form of triplets. Instead of triplets, we model the ranking list as a whole in the loss function, and propose a listwise multi-kernel similarity learning method, referred as SimListMKL. Experimental results on real world data set show that our proposed method SimListMKL outperforms the baselines approaches based on triplets.

similar App recommendation; multi-kernel learning; relative similarity; similarity learning; listwise learning

2016-04-14;收到修改稿时间:2016-05-12

[10.15888/j.cnki.csa.005502]