基于复杂网络的铁路-航空多层网络的鲁棒性研究
2017-10-12马夏夏蔡永明
马夏夏,蔡永明
(济南大学商学院,山东 济南 250002)
基于复杂网络的铁路-航空多层网络的鲁棒性研究
马夏夏,蔡永明*
(济南大学商学院,山东 济南 250002)
为提高我国交通系统运行的效率和稳定性,本文应用复杂网络理论,选取中国大陆(不包括港澳台)的地级市铁路和航空数据(截至2015年7月)为研究对象,构建了中国铁路-航空多层网络。对铁路-航空多层网络的拓扑性质和鲁棒性进行了研究,选取平均路径长度和网络效率两项指标作为鲁棒性评价指标。研究结果表明,铁路-航空多层及其单层网络都具有小世界和无标度特性;铁路-航空多层网络在蓄意攻击方式下的鲁棒性较差,而在随机攻击方式下的鲁棒性较强;不管是在蓄意还是随机攻击的方式下,铁路-航空多层网络的鲁棒性都要优于铁路层、航空层网络。
铁路-航空多层网络;复杂网络;鲁棒性;蓄意攻击;随机攻击
Abstract∶To improve the efficiency and stability of our traffic system operation, this paper applied the complex network theory, selected railway and airline data (as of July 2015) of the prefecture-level cities in China (not including Hong Kong, Macao and Taiwan) as the research object, and constructed the Chinese railway and airline multilayer networks. The topological characteristics and robustness of Chinese railway and airline multilayer networks were studied, and two indexes, such as average path length and network efficiency, were chosen as robustness evaluation indexes. The results include the following points: the railway and airline multilayer and its single-layer networks all have small-world and scale-free characteristics; the robustness of Chinese railway and airline multilayer networks is better under the random attack than under the calculated attack; the robustness of railway and airline multilayer networks is better than its two subnetworks, whether under the calculated attack or under the random attack.
Key words∶railway and airline multilayer networks; complex network; robustness; the calculated attack; the random attack
铁路和航空系统对我国的经济发展起着极其重要的促进作用,随着这两大交通系统的不断发展,人们对其运营的安全性、稳定性和高效性提出了更高的要求。近些年来,国内外对单一的铁路网络和航空网络的研究较多。拓扑特性方面,唐芙蓉等[1]分析了中国铁路网络的拓扑结构,结果表明其具有无标度特征的小世界网络特点;Bagler等[2-3]分别研究并证明了印度航空网络和意大利航空网络具有小世界特性。鲁棒性和可靠性研究方面,最早对复杂网络可靠性进行研究的是Albret等[4],他们使用最大簇S、孤立簇和平均路径长度L来衡量随机网络和无尺度网络在受到攻击后的被破坏程度。Holme等[5]使用最大连通子图和网络效率来衡量网络性能,并给出了不同的网络类型在不同攻击策略下的网络结构变化情况。Paul等[6]研究了如何用最大的效率和最小的成本来提高复杂网络的鲁棒性。Sohrabi等[7]对世界上33个城市的地铁网络进行了鲁棒性研究,并提出了提高其鲁棒性的可行性建议。叶婷婷[8]选取网络的效率作为全国铁路网络连通可靠性的衡量指标,分析了全国铁路网络在不同攻击方式下连通可靠性的变化情况。刘刚等[9]分析了铁路换乘系统的铁路线路网络模型和铁路站点网络在随机攻击和蓄意攻击下的鲁棒性。姜涛等[10-11]在离散有限情景集的基础上,建立了无容量限制的中国航空网络鲁棒性优化模型。曾小舟等[12]建立了网络抗毁性测度方法,对中国航空网络进行了抗毁性实证分析。徐凤等[13]对中国高铁-民航复合网络的拓扑性质和鲁棒性进行了研究。
由此可见,国内外对单一铁路网络和航空网络拓扑特性、可靠性、鲁棒性的研究已非常丰富,但对多种交通系统所构成的多层网络的研究却很少,从整体的角度,综合性地研究交通系统,描述其与子系统之间的关系,能够为交通系统的研究提供新思路。因此,本文构建了包含铁路系统和航空系统的多层网络,研究其拓扑特性与鲁棒性,并将多层网络的鲁棒性与铁路层、航空层网络的鲁棒性进行了比较,这对于探索铁路系统和航空系统之间是否存在合作空间以及挖掘出铁路与航空系统的综合功能具有非常重要的现实意义。
1 铁路-航空多层网络的构建及拓扑性质
1.1铁路、航空单层网络的构建
单层网络可以抽象为由点集V(G)和边集E(G)组成的图G=(V,E)。如果每一条边e都有一对与之相对应的点(i,j),点对(i,j)与(j,i)对应同一条边,这样的网络为无向网络;如果网络中的每条边都没有权重,则这样的网络为无权网络。本文所构建的单层网络为无向无权网络。
为了研究方便,本文在构建铁路、航空单层网络时,作了以下几点假设:
(1)对于铁路网络层,以火车站所在的城市作为节点,任意两个城市之间只要有同一列火车在这两个站点停靠,就认为这两个城市节点之间有边相连。
(2)对于航空网络层,以机场所在的城市作为节点,任意两个城市之间只要有同一航班可以到达,即认为两个城市节点之间有边相连。
(3)如果一个城市中同时有两个或两个以上的火车站,都认为该城市只有一个火车站节点;同理,如果一个城市中同时有两个或两个以上的机场,也都认为该城市只有一个机场节点。
(4)如果城市x到城市y有多列火车可以到达,则认为城市x与城市y之间只有一条连边,不存在重复连接;同理,如果两个城市之间有多列航班到达,则认为两个城市之间只有一条边相连。
(5)一般情况下,如果从x城市乘坐火车或航班到达城市y,那么也能够从城市y沿相同路线到达城市x。因此,不考虑城市节点之间的方向问题,将网络抽象为无向网络。
(6)不考虑火车及航班的频次和数量,也不考虑客运量等,即不考虑网络中的连边权重问题,将网络抽象为无权网络。
本文选取的是中国大陆(不包括港澳台)的地级市铁路和航空数据,截至2015年7月。其中,铁路数据共有58 296条,包括2 949个站点信息;航空数据共有100 235条,包括238个站点信息。由于这些数据中包含大量不相关的信息,因此需要按照构建单层网络的假设说明对这些数据进行处理。数据经过处理之后,使用R软件绘制出单层网络图,其中,铁路层网络包含268个节点和877条连边,航空层网络包含131个节点和1 439条边。
1.2铁路-航空多层网络的构建
多层网络可定义为一个三元组
将铁路-航空多层网络抽象为一个三元组

图1 铁路-航空多层网络图Fig.1 Topological diagram of the railway and airline multilayer networks
1.3铁路-航空多层网络及单层网络的拓扑性质
分别计算铁路-航空多层网络与单层网络的主要拓扑统计量,然后分析各网络的拓扑特性,如表1所示。

表1 铁路-航空多层网络与单层网络的主要统计量和拓扑特性
从表1中可以明显地看出,铁路-航空多层网络与单层网络都具有无标度特性和小世界特性。其中,无标度特性表明了网络具备增长性和择优连接的特性,即网络的规模会不断扩大,新加入的城市节点将倾向于连接网络中度值较大的城市节点;小世界特性则表明网络中虽然含有很多的城市节点,但要想从一个城市到达另一个城市,需要换乘的次数都是比较少的,铁路-航空多层网络需要2次换乘,铁路层网络、航空层网络和铁路-航空多层网络需要的换乘次数分别为3次、1次、2次。
从表1中可以看出,航空层网络的平均度、平均路径长度和聚类系数均优于铁路层网络;在铁路层网络的基础上,经过复合形成的多层网络的节点平均度增大,平均路径长度变小。节点的平均度增大,也就是网络中边的数量增加,表明人们有更多的出行路径可以选择,有利于缓解网络压力。平均路径长度变小则表明从一个城市到达另一个城市需要换乘的次数变少。
2 铁路层、航空层网络的鲁棒性研究
2.1网络鲁棒性的涵义及衡量指标
网络的鲁棒性是指当网络的内部结构发生变化或遭到外界破坏时,维持其原有功能的能力。对铁路-航空多层网络来说,鲁棒性指的是当遇到较差的天气、其他的突发事件而导致火车或飞机晚点、取消等问题时,即铁路-航空多层网络的节点或边会发生变化,还能够维持其网络连通性能的能力。
研究单层网络和多层网络的鲁棒性,可以通过分析网络在遭到攻击后其结构指标的关系变化(即被攻击节点数或被攻击节点比例与平均路径长度L、网络效率E的关系变化)来进行。
针对下面两个衡量指标中涉及到的节点i与节点j之间的距离dij定义如下:
当研究的网络是单层网络时,dij为连接节点i与节点j的最短路径上的边数;
当研究的网络是多层网络时,分为两种情况:一是节点i与节点j在同一层,dij为连接节点i与节点j的最短路径上的边数;二是节点i与节点j位于不同的层lm和ln时,dij为所有连接到层lm和ln中的节点以及两层间节点的最少边数[15]。
(1)平均路径长度L
网络的平均路径长度是指任意两个节点之间距离的平均值。一般情况下,平均路径长度越短,网络的连通性就越好。则网络的平均路径长度为:
其中,N为网络节点总数。
(2)网络效率E
图1所示为基于十字交叉压缩悬臂梁的变刚度微纳测头,它主要由测球、测杆、中心体、支撑梁、基座、H型柔顺机构、位移传感器及压电驱动装置等组成。
网络效率是衡量网络整体连通性的一个重要指标,将其定义为所有节点对之间的效率的平均值。计算公式为:
其中,N为网络节点总数,G为网络节点的点集,i,j∈G[16]。
理论上来说,网络瘫痪时,其效率应该为0。但是,在现实中当交通网络受到一定程度的攻击时,网络的效率就会变得很低,此时网络的整体性能已经变得很差。因此,本文中认为当E≤0.001时,网络瘫痪。
2.2铁路层、航空层网络的鲁棒性研究
复杂网络一般存在两种攻击方式,即随机攻击和蓄意攻击。所谓随机攻击是指网络的节点以某种概率被随机删除;而蓄意攻击又被称为选择性攻击,是指网络的节点按照某种策略被删除,删除节点的策略一般是从网络中度值最大的节点开始,每次都删掉网络中度值最大的节点。
研究复杂网络鲁棒性的具体方法是计算并分析网络受到随机攻击和蓄意攻击后平均路径长度L和网络效率E的数值变化,同时比较在不同攻击方式下同一衡量指标的数值变化。
图2与图3分别是铁路层与航空层网络的鲁棒性指标的数值变化图。由图2a和图3a可知,在两种攻击方式下,铁路层与航空层网络的效率E整体上都呈现出下降的趋势,但蓄意攻击方式下E的下降速度较快。由表2 ~5可以看出,铁路层与航空层网络在没有受到攻击时的效率E分别为0.290 4、0.573 7。随机攻击铁路层网络80个节点和航空层网络40个节点时,铁路层与航空层网络的效率E下降幅度较小,分别为0.242 2与0.514 9;而蓄意攻击铁路层网络80个节点和航空层网络40个节点时,铁路层与航空层网络的效率E会迅速下降至0.014 7与0.005 6,网络性能已变得较低。随机攻击铁路层网络258个节点和航空层网络127个节点时,铁路层与航空层网络的效率E下降为0,网络已完全瘫痪;而蓄意攻击铁路层网络153个节点和航空层网络48个节点时,就可以使网络几乎瘫痪。由此可以看出,在进行蓄意攻击时,先攻击度值较大的节点会使网络的拓扑结构迅速发生变化,较快地产生很多孤立节点,从而导致网络快速瘫痪;但在进行随机攻击时,恰好攻击到度值较大的节点的概率较小,只有随机攻击很多的节点才会导致网络瘫痪。因此,铁路层与航空层网络都是在随机攻击方式下的鲁棒性较强,而在蓄意攻击方式下的鲁棒性较差。

a 两种攻击方式下网络效率的数值变化 b 两种攻击方式下平均路径长度的数值变化图2 铁路层网络的鲁棒性指标Fig.2 The robustness indicator for the railway network

a 两种攻击方式下网络效率的数值变化 b 两种攻击方式下平均路径长度的数值变化图3 航空层网络的鲁棒性指标Fig.3 The robustness indicator for the airline network
由图2b和图3b可以看出,在随机攻击与蓄意攻击下,铁路层与航空层网络的平均路径长度L都是先增大,在若干次攻击之后L又开始减小,且在蓄意攻击方式下L的增大和减小的速度较快。一般地,平均路径长度L越小,网络的性能越好。结合表3和表5,蓄意攻击铁路层与航空层网络的节点数都小于40个时,其平均路径长度L都快速增大,网络的性能变差,但此时网络中并没有产生孤立的节点;当蓄意攻击铁路层与航空层网络的节点数都超过40个时,其平均路径长度L都开始急剧下降,但这并不意味着网络的性能变好,还需要根据网络的效率来判断网络的性能。从上述单层网络的效率的分析中可以看出,铁路层与航空层网络的效率一直都处于下降的状态,说明网络的性能在不断变差;当蓄意攻击铁路层与航空层网络的节点数达到153个与48个时,L的值都变为无穷大,此时铁路层与航空层网络已经瘫痪。结合表2与表4,在随机攻击方式下,平均路径长度L一直处于较小幅度的上升状态,直到攻击铁路层与航空层网络的节点数达到180个与120个时,L才有明显的下降趋势;当攻击铁路层与航空层网络的节点数为258个与127个时,L的值都变为无穷大,此时铁路层与航空层网络才处于瘫痪状态。因此,平均路径长度L的变化也说明了铁路层网络在随机攻击方式下的鲁棒性较强,而在蓄意攻击方式下的鲁棒性较差。

表2 随机攻击方式下铁路层网络鲁棒性指标计算结果

表3 蓄意攻击方式下铁路层网络鲁棒性指标计算结果

表4 随机攻击方式下航空层网络鲁棒性指标计算结果

表5 蓄意攻击方式下航空层网络鲁棒性指标计算结果
3 铁路-航空多层网络的鲁棒性研究
3.1铁路-航空多层网络的鲁棒性研究
图4是铁路-航空多层网络鲁棒性指标的数值变化图。由图4a可知,在两种攻击方式下,铁路-航空多层网络的效率E整体来说都是不断下降的,但蓄意攻击方式下E的下降速度较迅速。结合表6和表7可知,铁路-航空多层网络的初始效率E为0.343 8。随机攻击多层网络250个节点时,其效率减小到原来的一半;当随机攻击多层网络390个节点时,其效率E才减小到0。而在蓄意攻击方式下,当攻击多层网络53个节点时,其效率E就已减小到原来的一半;当攻击节点的个数达到210个时,其效率E为0.001 0,此时多层网络几乎瘫痪。因此,铁路-航空多层网络也是在随机攻击方式下的鲁棒性较强,而在蓄意攻击方式下的鲁棒性较差。
由图4b可以看出,两种攻击方式下,铁路-航空多层网络的平均路径长度L都是先增大,在若干次攻击之后又开始减小。结合表6和表7可以得出,在随机攻击方式下,平均路径长度L一直呈现小幅度的上升趋势,直至攻击节点达到300个时,L才有很明显的下降趋势;当攻击节点增加至390个时,L的值才变为无穷大,此时铁路-航空多层网络瘫痪。而在蓄意攻击方式下,当攻击节点的个数小于100时,L一直处于快速上升的趋势;当攻击节点的个数超过100时,L急剧下降。从上述多层网络的效率分析中可以看出,网络效率也一直下降,说明网络的性能在不断变差;当攻击节点的个数为210时,L的值变为无穷大,此时铁路-航空多层网络已经瘫痪。因此,平均路径长度L的变化也说明了铁路-航空多层网络在随机攻击方式下的鲁棒性较强,而在蓄意攻击方式下的鲁棒性较差。
由以上的分析可知,网络中度值较大即重要的节点对于多层网络与单层网络的整体连通性起到了极其重要的作用,多层网络与单层网络在蓄意攻击方式下的鲁棒性较差,维持其原有的网络连通性的能力较弱,而在随机攻击方式下的鲁棒性较强。结合现实生活中的情况,在随机攻击的方式下,假设个别的火车站点或机场受到恶劣天气的等情况的破坏,几乎不会影响到多层网络与单层网络的整体运输能力。但是如果大量的火车站点或机场同时遭到破坏,多层网络与单层网络的效率才会受到很大的影响。在蓄意攻击的方式下,假设多层网络与单层网络中少数重要的换乘站点被依次破坏,会导致网络的效率快速下降。
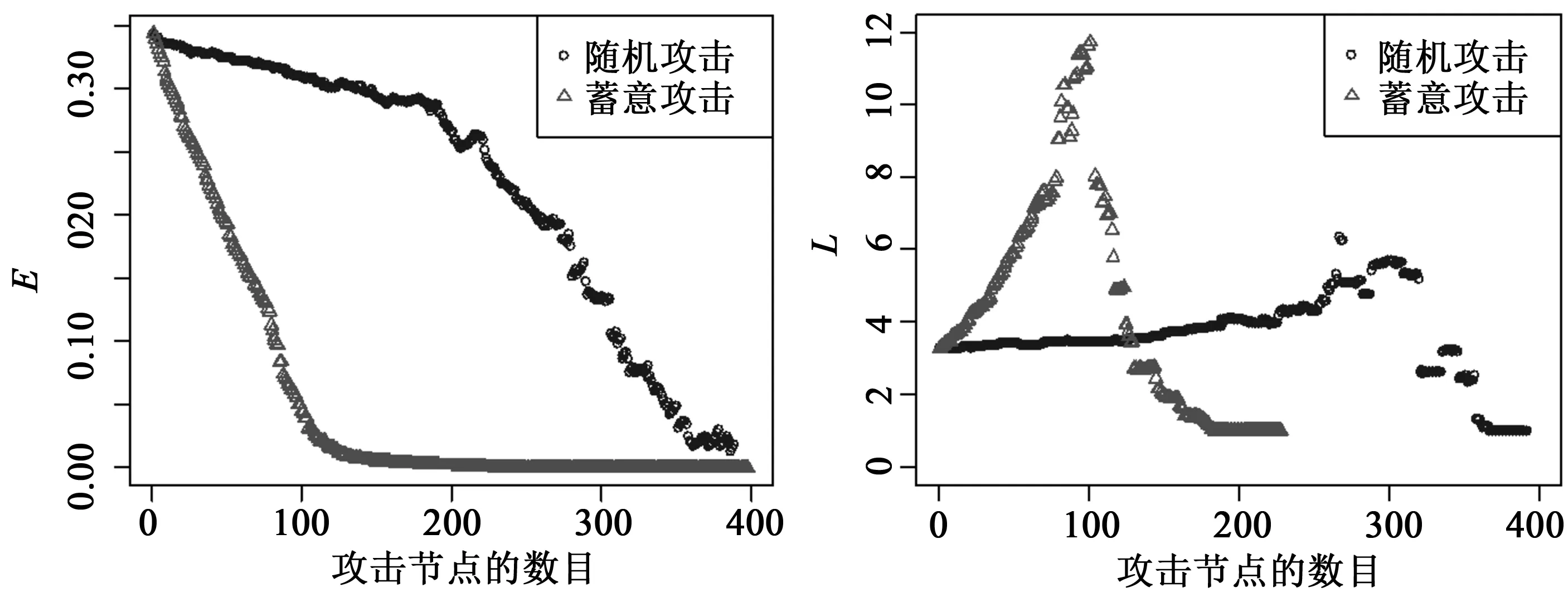
a 两种攻击方式下网络效率的数值变化 b 两种攻击方式下平均路径长度的数值变化图4 铁路-航空多层网络的鲁棒性指标Fig.4 The robustness indicatorfor railway and airline multilayer networks

表6 随机攻击方式下铁路-航空多层网络鲁棒性指标计算结果

表7 蓄意攻击方式下铁路-航空多层网络鲁棒性指标计算结果
3.2多层网络的鲁棒性与单层网络的鲁棒性的比较
图5是随机攻击方式下铁路-航空多层网络与铁路层网络、航空层网络的鲁棒性指标变化图。如图5a所示,在随机攻击的方式下,随着攻击节点数的增多,铁路-航空多层网络与铁路层、航空层网络的平均路径长度都是先增大再减小。虽然L的减小也并不能说明网络的整体连通性变好,而是要根据网络的效率来说明此时网络的整体连通性的变化,但是多层网络平均路径长度增大和减小的速度是最慢的,这就可以说明多层网络的鲁棒性比铁路、航空单层网络的鲁棒性要强。
如图5b所示,铁路-航空多层网络与铁路层网络、航空层网络在随机攻击方式下,网络的效率E都是不断减小直到为0。铁路层网络和航空层网络分别在随机攻击了258和127个节点后,其效率减小至0,此时网络已经瘫痪;而铁路-航空多层网络的初始效率为0.343 7,在随机攻击了390个节点之后,其效率才减小至0,此时多层网络瘫痪。也就是说,在随机攻击方式下,多层网络的效率下降速度是最慢的,即铁路-航空多层网络的鲁棒性比铁路层、航空层网络的鲁棒性强。

a 平均路径长度 b 网络效率图5 随机攻击下多层网络与单层网络的鲁棒性指标变化比较 Fig.5 Comparison of robustness indicator changes between multilayer networks and single layer networks under random attack
图6是蓄意攻击方式下铁路-航空多层网络与铁路层网络、航空层网络的鲁棒性指标变化图,与上述随机攻击方式下分析网络鲁棒性指标的方法一样,但是在蓄意攻击方式下,各个网络的鲁棒性指标的变化会相对剧烈。由图6a可以看出,在蓄意攻击的方式下,随着攻击节点数的增多,各个网络的平均路径长度都是先快速增大再快速减小。同样地,多层网络L的增大和减小速度最为缓慢,这就足以说明,在蓄意攻击方式下,铁路-航空多层网络的鲁棒性是优于铁路层和航空层网络的。
由图6b所示,蓄意攻击方式下,各个网络的效率都是随着攻击节点数目的增多而快速减小直至为0,多层网络效率的下降速度也是最慢的。铁路层网络、航空层网络和铁路-航空多层网络在受到蓄意攻击的节点数分别达到153、48和210时,其效率分别为0.000 8,0.000 9和0.001 0,此时网络都已完全瘫痪。因此,在蓄意攻击方式下,铁路-航空多层网络的鲁棒性还是比铁路层、航空层网络的鲁棒性强。

a 平均路径长度 b 网络效率图6 蓄意攻击下多层网络与单层网络的鲁棒性指标变化比较Fig.6 Comparison of robustness indicator changes between multilayer networks and single layer networks under calculated attack
4 结论
本文运用复杂网络的相关理论,选取中国大陆(不包括港澳台)的地级市铁路和航空数据(截至2015年7月)为研究对象,分别构建了中国铁路-航空多层网络和铁路层、航空层网络,研究了其网络特性与鲁棒性,并将其鲁棒性进行了比较。结果表明,铁路-航空多层网络的鲁棒性在随机攻击的方式下较强,而在蓄意攻击方式下较弱,所以要特别重视对重要站点的保护,以提高多层网络的抗攻击能力;不论是在随机攻击还是蓄意攻击的方式下,铁路-航空多层网络的鲁棒性都比铁路层、航空层网络的鲁棒性强,这说明了加强铁路系统和航空系统之间的合作可以提高整体交通网络的鲁棒性。
本文构建的多层交通网络只包含了铁路、航空两层的无权无向复杂网络,后续的研究可以将公路交通网络和水运交通网络都融入到多层交通网络中,同时可以考虑将客运量、发车频次、航空班次等因素转化为网络权重,从而研究加权交通网络。
此外,本文构建的多层网络是静态的复杂网络,但是复杂网络并不是一成不变的,而是随着时间的推移而不断演化的动态网络。对于交通网络而言,随着铁路线路的不断开通和通航城市的不断增加,铁路-航空多层网络中将会拥有越来越多的节点,后续可以研究多层网络的动态演化规律等。
[1]唐芙蓉,杨先清,唐刚,等.中国铁路交通网络的拓扑研究及客流分析[J].中国矿业大学学报,2010,39(6):935-940.
[2]BAGLER G. Analysis of the airport network of India as a complex weighted network [J].Physica A: Statistical Mechanics and its Applications, 2008, 387(12):2972-2980.
[3]GUIDA M, MARIA F. Topology of the Italian airport network: A scale-free small-world network with a fractal structure [J].Chaos, Solitons and Fractal, 2007, 31(3):527-536.
[4]ALBERT R, JEONG H, BARABASI A L. Error and attack tolerance of complex networks [J].Nature,2000, 406(6794):378-382.
[5]HOLME P, KIM B J, YOON C N, et al. Attack vulnerability of complex networks [J].Physical Review E, 2002, 65(5):056109.
[6]PAUL G, TANIZAWA T, HAVLIN S, et al. Optimization of robustness of complex networks [J].The European Physical Journal B, 2004, 38(2):187-191.
[7]SOHRABI K, MERRILL W, ELSON J, et al. Methods for scalable self-assembly for ad hoc wireless sensor networks [J].IEEE Transactions on Mobile Computing, 2004, 3(4):317-331.
[8]叶婷婷.基于复杂网络的全国铁路网络连通可靠性分析[D].北京:北京交通大学,2009.
[9]刘刚, 李永树. 基于复杂网络理论的铁路换乘系统鲁棒性分析[J].计算机应用研究,2014, 31 (10):2941-2942.
[10]姜涛, 朱金福,覃义.基于最短路的中枢辐射航线网络鲁棒优化方法[J].系统工程,2007,25(1):53-59.
[11]柏明国,姜涛,朱金福.基于禁忌算法的中枢辐射航线网络鲁棒优化方法[J].数学的实践与认识,2008,38(13):60-69.
[12]曾小舟,唐笑笑,江可申.基于复杂网络理论的中国航空网络抗毁性测度分析[J].系统仿真技术,2012, 8(2):111-116.
[13]徐凤,朱金福,苗建军.基于复杂网络的空铁复合网络的鲁棒性研究[J].复杂系统与复杂性科学,2015, 12(1):40-45.
[14]BRODKA P, SKIBICKI K, KAZIENKO P, et al. A degree centrality in multi-layered social network[C]// 2011 International Conference on Computational Aspects of Social Networks (CASoN). [S.l.]: IEEE,2011:237-242.
[15]GAO J X,BULDYREV S V,STANLEY H E, et al. Networks formed from interdependent networks[J].Nature Physics,2011,8(1):40-48.
[16]赖丽萍.城市轨道交通网络鲁棒性研究[D].北京:北京交通大学,2012.
Study on the robustness of Chinese railway and airline multilayer networks based on complex network theory
MA Xia-xia, CAI Yong-ming*
(School of Management, University of Jinan, Jinan, 250002, China)
TP397
A
1002-4026(2017)05-0070-09
10.3976/j.issn.1002-4026.2017.05.012
2016-11-23
山东省社会科学规划研究项目(14CGLJ03)
马夏夏(1992—),女,硕士研究生,研究方向为复杂网络数据挖掘。E-mail:734042637@qq.com
