非阿基米德2-赋范空间的等距问题

马玉梅

(大连民族大学 理学院，辽宁 大连 116605)

非阿基米德2-赋范空间的等距问题

马玉梅

(大连民族大学 理学院，辽宁 大连 116605)

推广了Mazur-Ulam定理和Aleksbndrov 问题到非阿基米德2-赋范空间。 证明了两个非阿基米德空间的任何2-等距是仿射的；一个单位距离保持映射是2-等距当且仅当它保持零距离。

Mazur-Ulam定理；Aleksandrov 问题；等距；非阿基米德空间

Abstract:This paper generalizes the Mazur-Ulam theorem and the Aleksandrov problem on non-Archimedean 2-normed spaces. It proves that any 2-isometric mapping between two non-Archimedean 2-normed spaces is affine; and a one-distance preserving mapping is 2-isometric if and only if it has zero-distance preserving property.

Keywords:Mazur-Ulam theorem; Aleksandrov problem; isometry; non-Archimedean spaces

1 研究的理论背景

设X和Y是度量空间，称映射f:X→Y为等距映射，对任意x,y∈X有dX(x,y)=dY(f(x),f(y))。

1932年Mazur 和 Ulam 在赋范空间给出了“满”等距算子必为仿射算子[1]。此后“非满”等距延拓为线性或仿射的问题一直是80多年以来研究的热点。1970年Aleksandrov提出度量空间中保持单位距离的映射是否为等距映射[2]，1987年J. Baker 得到严格凸空间的等距单映射必为仿射的[3]。

针对以上问题的研究主要在两类空间展开。

(1) 赋范空间。W. Benz 推广了Aleksandrov 问题,给出了保持两个常数距离的映射为等距的条件[2]。T. M. Rassias 证明了满足Lipschitz 条件的强保持单位距离(双射均保持单位距离(SDOPP))映射是等距算子[4]。马玉梅推广了T. M.Rassias 和W. Benz的结论到严格凸赋范空间去掉了满射条件,给出满足Lipschitz 条件的保持距离1的映射(DOPP)可以等距延拓到全空间[4]。

(2) n-赋范空间。2004年起，H.Chu,C.Park, T.M. Rassias，高金梅、任卫云、靖阳平等将Aleksandrov 问题推广到2-赋范和n-赋范空间[5-22]；C. Park 和 T.M. Rassias 给出了n-距离下满足n-DOPP,n-Lipschitz 以及保持m-colinear (m=2,n)等条件的映射是n-等距的[6-7]。H. Gunawan 和 M. Mashadi 给出了范数降维理论[18,20]，为进一步解决n-赋范空间中维数限定问题提供了重要依据。基于此理论马玉梅得到了n-赋范空间中保持单位距离为等距的充要条件是该映射保持零距离。

1897年, Hensel发现在复分析中起重要作用的了p-adic 数。p-adic 导出的范数称为非阿基米德范数。最近三十年非阿基米德分析引起了物理学家的广泛注意。2008年起Mohammd S与 Ghardir, 给出了非阿基米德n-赋范空间的Mazur-Ulam定理，在不同的条件下证明三角形的重心保持不变性[20]。

本文将着重阐述非阿基米德2-赋范空间中的最新结果，将n-赋范空间的结果推广到非阿基米德2-赋范空间。

2 基本术语

K是一个非阿基米德值域，如果|·|na为K 到[0,∞)的映射，满足对任意r,s∈ K,

(1) |r|na= 0 当且仅当r= 0;

(2) |rs|na= |r|na|s|na;

(3) |r+s|na≤ max{|r|na,|s|na}。

自然数集N上的非阿基米德域显然有：|1|na= |-1|na= 1 且|n|na≤ 1 (任意n ∈ N)。

N上的另外一个平凡的非阿基米德值域K ：|·|na将0映为0，将非0映为1[16]。

非阿基米德2-赋范空间的研究依赖于非阿基米德值域。

定义1[17]：设X是值域K上的向量空间，k是X上的非阿基米德范数k:X→ [0,∞)，对任意r∈K 以及x,y∈X,有

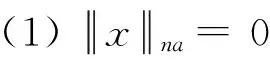
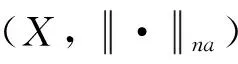
定义2[17]：设X是实向量空间且dimX≥ 2，x1,x2∈X,r∈K，||·,·||na是一个函数，满足

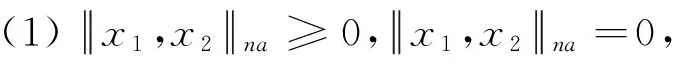
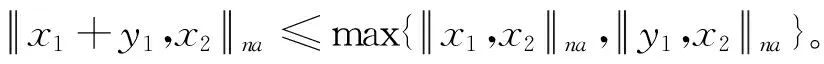
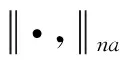
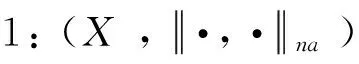
注2：本文设非阿基米德域Ω[18]满足如下条件: (r∈Ω,

设X和Y是域Ω上的非阿基米德2-赋范空间(dimX≥ 2)。

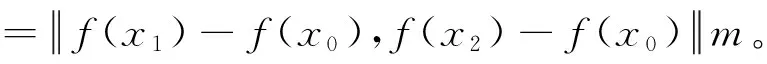
定义 6[17]：称f:X→Y为2-等距(2-isometry)，如果对任意x1,x2,y1,y2∈X,‖x1-y1,x2-y2‖=‖f(x1)-f(y1),f(x2)-f(y2)‖。

定义 7[17]：称f:X→Y为2-距离1保持(2-DOPP), 如果‖x1-y1,x2-y2‖=1 则‖f(x1)-f(y1),f(x2)-f(y2)‖=1。

定义 8[17]：称f:X→Y为保持2-共线(2 -collinear),如果对x,y,z∈X:存在t∈R，使得z-x=t(y-x)，那么存在s∈R使得f(z)-f(x) =s(f(y)-f(x))。

3 主要结果

证明：

设x0,x1∈X。由于dimX≥ 2,那么存在x2∈X满足x1-x0,x2-x0是线性无关的。这样‖x1-x0,x2-x0‖≠0。令：z2=x0+‖x1-x0,x2-x0‖(x2-x0)。

于是‖x1-x0,z2-x0‖=|‖x1-x0,x2-x0‖|na·‖x1-x0,x2-x0‖=1。因为f有w-n-DOPP,所以‖f(x1)-f(x0),f(z2)-f(x0)‖=1。

可见f(x0)≠f(x1)，所以f是单射。

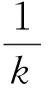
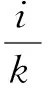
(1)

式中,i=0,1,…,k。

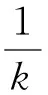
根据注1得到

(2)

(3)

由于ui,ui-1,ui+1是2-共线，并且f保持2-共线,则必存在α∈R,使得

f(ui+1)-f(ui)=α(f(ui)-f(ui-1))。

(4)

既然f保持w-n-DOPP,那么

‖f(ui+1)-f(ui),f(vk)-f(ui)‖=1,‖f(ui)-f(ui-1),f(vk)-f(ui)‖=1。

于是,‖α(f(ui)-f(ui-1)),f(vk)-f(ui)‖=1。Thus|α|na·‖(f(ui)-f(ui-1)),f(vk)-f(ui)‖=1,于是|α|=1。

由于f是单射，根据公式(3)、(4)有α=1,

f(uk)-f(x0)=k(f(u1)-f(x0))。

(5)

根据式(1),‖u1-x0,x2-x0‖=1，这样,‖f(u1)-f(x0)),f(x2)-f(x0)‖=1。

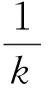
引理2：如果f:X→Y满足w-2-DOPP和保持2共线，那么f保持有理数距离。

证明：

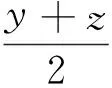
(6)

由于dimX≥2,那么存在x1∈X使得‖y-x,x1-x‖≠0。

令：w=x+‖y-x,x1-x‖(x1-x)。于是

‖y-x,w-x‖=1,且‖f(y)-f(x),f(w)-f(x)‖=1。

(7)

由式(6)可得‖f(z)-f(x),f(w)-f(x)‖=|s|。

(8)

根据y-x=x-z得到‖z-x,w-x‖=1,以及

‖f(z)-f(x),f(w)-f(x)‖=1。

(9)

由于f是单射,比较式(8)与式(9)得到s=-1，意味着

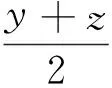
令g(x)=f(x)-f(0)。显然对任意x∈X以及任意有理数r、p,有g(rx)=rg(x),g(rx+py)=rg(x)+pg(y)。

(10)

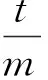
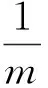
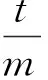
引理3：设X假设f:X→Y满足w-2-DOPP并且保持2-共线,这样f是仿射的。

证明：

可参见文献[22]。非阿基米德范数不影响使用相同的方法，该方法是对文献[16]的修正。

定理1：假设f:X→Y满足w-2-DOPP并且f是仿射的,那么f保持0-距离;f保持2-DOPP;f是2等距。

证明：

令g(x)=f(x)-f(0),那么g(x)是线性映射。

(1)假设‖y1-x1,y2-x2‖=0,这样{y1-x1,y2-x2}是线性相关的。于是存在不全为零的两个元素a1、a2，使得a1(y1-x1)+a2(y2-x2)=0,这样a1(g(y1)-g(x1))+a2(g(y2)-g(x2))=0。

显然‖g(y1)-g(x1)g(y2)-g(x2)‖=0,于是‖f(y1)-f(x1),f(y2)-f(x2)‖=0。

(2)假设x1,x2∈X,‖y1-x1,y2-x2‖=1,任取x0∈X, 令zi=x0+yi-xi,那么‖z1-x0,z2-x0‖=1。

这样：‖f(z1)-f(x0),f(z2)-f(x0)‖=1以及‖g(z1)-g(x0),g(z2)-g(x0)‖=1。

由于g是线性的，意味着‖g(y1)-g(x1),g(y2)-g(x2)‖=1，于是‖f(y1)-f(x1),f(y2)-f(x2)‖=1。

(3)假设x1,x2,y1,y2∈X,‖y1-x1,y2-x2‖≠0，

令：y=x1+‖y1-x1,y2-x2‖(y1-x1)

(11)

那么‖y-x1,y2-x2‖=1且‖f(y)-f(x1),f(y2)-f(x2)‖=1。

因此‖g(y)-g(x1),g(y2)-g(x2)‖=1。

(12)

由g的线性性质可得|‖y1-x1,y2-x2‖|na‖(g(y1)-g(x1)),g(y2)-g(x2)‖=1。

这样：‖|y1-x1,y2-x2‖|na‖(f(y1)-f(x1)),f(y2)-f(x2)‖=1。推得‖f(y1)-f(x1),f(y2)-f(x2)‖=‖y1-x1,y2-x2‖,于是f是一个等距。

[1] MAZUR S，ULAM S. Sur les transformationes isometri-ques d′espaces vectoriels′ normes [J]. C. R. Acad. Sci. Paris, 1932(194)：946-948.

[2] ALEXANDROV D.Mappings of families of sets [J]. Soviet Math. Dokl., 1970 (11): 116-120.

[3] BENZ W. Isometrien in normierten Raumen [J]. Aeq. Math., 1985 (29): 204-209.

[4] RASSIAST，SEMRL P. On the Mazur-Ulam theorem and the Aleksandrov problem for unit distance preserving mappings [J]. Proc. Amer. Math. Soc. 1993 (118): 919-925.

[5] MA Yumei.The Aleksandrov problem for unit distance preserving mapping [J]．Acta Math. Sci. Ser. B Engl. Ed., 2000 (20): 359-364.

[6] CHU H LEE K，PARK C.On the Aleksandrov problem in linear n-normed spaces [J]. Nonlinear Anal. 2004 (59): 1001-1011.

[7] PARK C，RASSIAS T.Isometries on linear n-normed spaces [J]. JIPAM. J. Inequal. Pure Appl. Math., 2006 (7): 1-17.

[8] PARK C, ALACA C. A new version of Mazur-Ulam theorem under weaker conditions in linear n-normed spaces [J]. Journal of computational analysis and application, 2014 (16): 827-832.

[9] GAO Jinmei. On the Alexandrov problem of distance preserving mapping [J]. J. Math. Anal. Appl., 2009 (352): 583-590.

[10] JING Yangping.The Aleksandrov problem in p-normed spaces (0 < pleq 1) [J]. Acta Sci. Nat. Univ. Nankai., 2008 (4):91-96.

[11] CHU H，CHOI S，KANG D. Mapping of conservative distance in linear n-normed spaces [J]. Nonlinear Anal., 2009 (70):1168-1174.

[12] GUNAWAN H， MASHADI M. On n-normed spaces [J]. Int. J. Math. Math. Sci., 2001 ( 27): 631-639.

[13] MA Yumei.The Aleksandrov problem and The Mazue-Ulam Theorem on Linear n-normed space [J]. Bull. Korean Math. Soc., 2013 (50): 1631-1637.

[14] MA Yumei. On the Aleksandrov-Rassias Problems on Linear n-Normed Spaces [J]. Journal of Function Spaces and Applications，2013 (394216): 1-7.

[15] EKARIANI S, GUNAWAN HIDRIS M. A contractive mapping theorem on the n-normed space of p-summable sequences [J]. Journal of Mathematical Analysis, 2013 ( 4), 1-7.

[16] MA Yumei. Isometries on linear n-normed spaces[J].Annales Academiae Scientiarum Fennicae-Mathematica, 2014(39): 973-981.

[17] WANG Danping, LIU Yubo SONG Meimei. The Aleksandrov problem on non-Archimedean normed space [J]. Arab J. Math. Sci., 2012 (18): 1319-5166.

[18] CH H, KU S.A Mazur-Ulam problem in non-Archimedean n-normed spaces [J]. Journal of inequalities and applications, 2013 (34): 1-10.

[19] ANDREI K.Non-Archimedean Analysis: Quantum Paradoxes, Dynamical Systems and Biological Models[J]. Mathematics and Its Applications, 1997 (427): 101-129.

[20] SAL MOSLEHIAN M，GHARDIR S.A Mazur-Ulam theorem in non-Archimedean nomed spaces [J]. Nonlinear Anal., 2008 (69): 3405-3408.

[21] CHEN Xiaoyun，SONG Meimei，Characterizations on isometries in linear n-normed spaces [J]. Nonlinear Anal., 2010 (72): 1895-1901.

[22] HUANG Xujian，TAN Dongni.Mappings of preserving n-distance one in n-normed spaces[EB/OL].[2016-09-20] .https://arxiv.org/pdf/1609.06033.pdf.

(责任编辑 王楠楠)

TheIsometricProblemonNon-Archimedean2-normedSpaces

MAYu-mei

(School of Science, Dalian Minzu University, Dalian Liaoning 116605, China)

O177.3

A

2017-05-06；

2017-07-22

中央高校基本科研业务费专项资金资助项目(DC201502050301)。

马玉梅(1962-)，女，辽宁海城人，教授，博士，主要从事泛函分析理论及其应用研究。

2096-1383(2017)05-0474-04