基于FOA-SVM模型的输油管道内腐蚀速率预测
2017-10-11吴庆伟王金龙张平
吴庆伟,王金龙,张平
基于FOA-SVM模型的输油管道内腐蚀速率预测
吴庆伟,王金龙,张平
(中国特种设备检测研究院,北京100029)
针对管道内腐蚀速率相关问题,采集某输油管道内腐蚀的实测数据,应用多元统计分析算法,在支持向量机(SVM)的基础上建立管道内腐蚀速率预测模型。采用果蝇优化算法(FOA)对预测模型进行优化训练,建立FOASVM预测模型,利用实测数据样本对模型的预测结果进行检验。结果表明:综合方差和均差分别为1.397×10-3和0.037 4,FOA-SVM预测模型相比灰色组合模型预测值和最小二乘支持向量机(LS-SVM)模型预计结果稳定性好、精度高,但是FOA-SVM预测模型训练时间较长,今后在提高模型预测效率上需要进一步研究。
管道内腐蚀速率;支持向量机SVM;果蝇算法FOA;多元统计分析
Abstract:Using multivariate statistical analysis method,a new prediction model for pipeline internal corrosion rate was put forward on the basis of support vector machine(SVM)by collecting the measured data of internal corrosion rates of the oil pipeline.Fruit flies optimization algorithm(FOA)was used to optimize the training of prediction model and establish the FOA-SVM forecasting model.The forecast result was checked by using measured sample data.Considering that the integrated variance was 1.397×10-3and the mean deviation was 0.037 4,the FOA-SVM prediction model had better stability and higher precision compared with the grey combinational model.However,due to the longer training time of the FOA-SVM prediction model,further study is still needed to improve the model prediction efficiency.
Key words:internal pipeline corrosion rate;support vector machine SVM;fruit flies optimization algorithm(FOA);multivariate statistical analysis
据不完全统计,我国油田生产现状已进入中、高含水期,由于输油管道服务年限的延续,内腐蚀损伤长度不断增加,穿孔事故频发,仅东部油田各类管道穿孔损伤每年达2万余次,更换管道长度约400 km/a,给油田带来了巨大的经济损失。基于此,众多专家学者在管道内腐蚀预测方法方面进行了大量的研究[1-6]。刘晓东等[4]将灰色系统理论、人工神经网络及时间序列分析方法相结合,建立灰色组合模型,通过对腐蚀速率测量数据序列的趋势性、周期性及随机性成分分别建模,从而实现对腐蚀速率的预测;王晓光等[5]建立LS-SVM组合模型对管道腐蚀速率进行预测,展示了变权组合在提高预测精度和稳定性方面的优势。本工作采用FOASVM模型预测了输油管道内的腐蚀速率,对比分析了FOA-SVM模型、灰色组合模型、LS-SVM模型,以期为预测管道内腐蚀速率提供一种新方法。
1 SVM基本理论
SVM是由统计学理论而来,主要针对小样本数据进行学习、分类和预测的一种方法,将“低维空间”上的点或线映射到"高维空间",寻找一个平面将这些点或线分离,这种线形函数统称为“超平面”[7-8]。通过松弛变量和核函数(Kernel)处理实现低维到高维的转化,线性由不可分转化为可分,最后对转化之后的样本进行线性分析[9-11]。
假设样本为(x1,x2,…xn.)∈Rn,(y1,y2,…yn.)∈R,x∈R为输入参数,y∈R为相应的输出参数,n为样本个数。SVM的转化过程就是建立一个非线性映射φ,将数据x映射到高维特征空间F,回归函数为[12]:
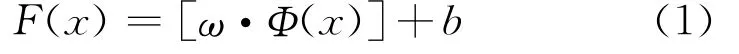
根据多元统计分析理论,可通过以下目标数极小化确定SVM回归函数:
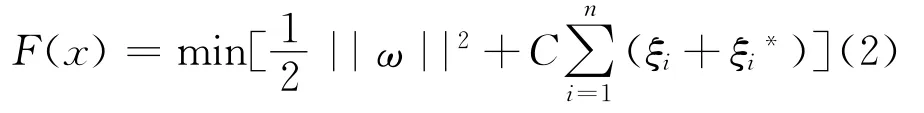
约束条件为
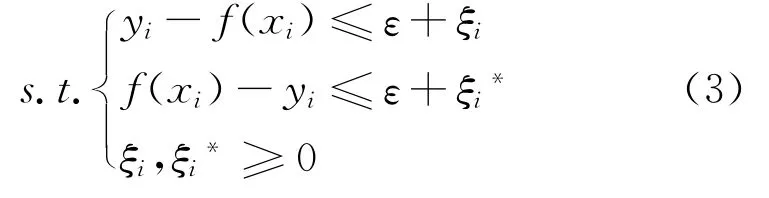
拉格朗日对偶性变量约束优化
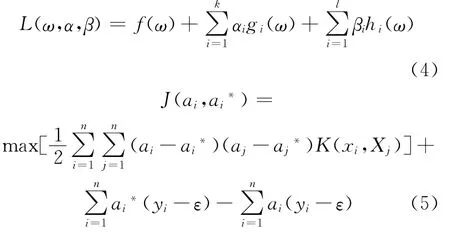
约束条件为
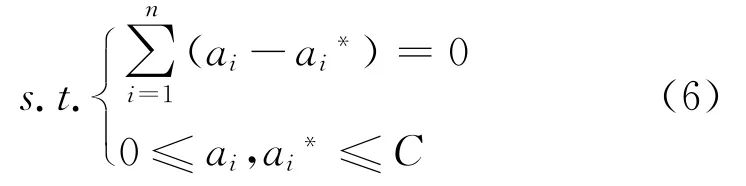
式中:ai,ai*为拉格朗日系数;αi,βi为拉格朗日算子;b这临界值;ω为权值矢量;ξ,ξ*为非负松弛变量;C为惩罚变量;ε为不敏感损失函数参数;K(xi,xj)为SVM的核函数。
核函数是计算两个向量在隐式映射空间中的内积函数,将低维空间中向量通过变换得到高维空间量的向量内积值,文中选用高斯径向基核函数,即:K(xi,xj)=exp(-g|xi-xj|2),g为核函数的参数宽度。
通过以上的理论推导可得到回归函数为
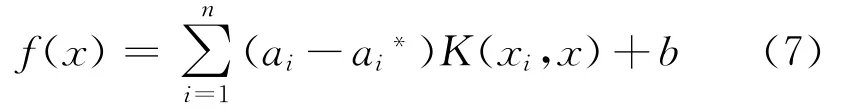
对于新的输入参数x可通过该式计算得到相应的输出值。
2 果蝇算法优化支持向量机
果蝇优化算法是一种基于果蝇觅食行为而推演出寻求全局智能优化的新方法,属于演化式计算的范畴,亦属于人工智能的领域,可混合其他方法与管道内腐蚀技术一起使用,如模糊数学、经验公式、灰色系统与神经网络等。通过果蝇自身位置来估计周围的味道浓度,随后果蝇向味道浓度的极值方向飞去,重复迭代味道浓度求取目标函数的最优解[13-16]。
由于果蝇是在三维空间飞行,而原始的FOA算法是在二维空间搜寻全局极值,因此将可能无法搜寻到三维空间中的最佳值,因此本工作采用三维空间搜寻,对FOA进行改进。
FOA对SVM优化的具体步骤,见图1所示。
第二,多重困境儿童。在实际中,很多儿童可能即属于生理性困境儿童,也属于社会性困境儿童。多重困境是非常常见的现象。困境儿童概念体系的建立有助于帮助辨认最困难的儿童群体。
图1中:Rran为随机数;i=1,2,…,m;yij为真实值;m为各个交叉验证训练子集的果蝇数目;f(xij)为交叉训练的预测值;bF为F的最大值;bI为F最大值所处的位置。
因为SVM的优化参数是C和G,所以X和Y均为m行2列矩阵。采用迭代的方法对参数进行优化,同时判定味道浓度相比上一次迭代的味道浓度变化,如果优于上一步迭代则转至步骤(7),否则继续循环直至达到指定循环次数N时,循环终止。
3 FOA-SVM管道内腐蚀速率预测模型
某输油管道材质为20号钢,1990年10月建成投产,使用压力为1.0~5.0 MPa,输送介质为产地不同的原油,影响管道内腐蚀速率主要参数为硫含量、酸值、温度、流速、压力,实测数据统计见表1。将影响内腐蚀速率的参数作为输入向量,内腐蚀速率作为输出向量,建立FOA-SVM预测模型。选取某输油管道内腐蚀速率实测数据1~25组样本作为训练集,以徐州管道局输油管道试验数据作为测试集,采用实测值与灰色组合模型、LS-SVM模型、FOA-SVM模型预计值对比分析的方法,对FOASVM模型的性能进行评价。
3.1 建立回归模型
将参数值输入SPSS软件,设腐蚀速率y为因变量,硫含量xi、酸值x2、温度x3、流速x4、压力x5为自变量。FOA-SVM多元线性回归模型采用逐步回归的方法,针对影响因素变量对因变量的影响程度进行分析比较。建立多元性回归模型时,为了使得回归模型具有良好的解释能力和预测效果,自变量的选择准则如下:
(1)自变量对因变量呈线性相关,且影响效果显著;
(2)相关程度比较,自变量之间应低于因变量与自变量之间的的相关程度;
(3)预测值的确定,自变量应完全满足因变量的统计数据。

图1 FOA优化SVM步骤图Fig.1 FOA optimized SVM step figure

表1 某输油管道内腐蚀速率实测数据统计表Tab.1 Statistical table of internal corrosion rate measurement data for an oil pipeline
优选自变量过程中,当回归方程中所有自变量对因变量各自影响显著时,再考虑从其他未选中变量代人方程,循环往复直至所有自变量优选后,求解结束。由逐步回归法得到的回归方程为
y=0.072x1+0.054x2+0.013 (8)
由此可以看出,逐步回归忽略了温度、流速两个变量,压力对管道的腐蚀速率影响不大。而回归方程中硫含量和酸值的Sig值都为0,具有统计显著性。得到的回归方程的调整R2为0.307,具有较好的拟合优度。
对模型所有数据进行残差分析,优化模型。结果显示6、8、9号三组数据的残差绝对值残差较大,忽略这三组数据,重新建立回归方程,调整R2为0.426,满足要求。得到结果为
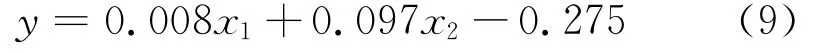
3.2 腐蚀速率预测及分析
基于FOA模型优化回归参数C和G,设定群体个数为20,遗传代数为200,C参数范围[0,500],G参数范围[0,100]。得到的优化参数C1和G1为0.041和0.012 8输入FOA-SVM模型训练,结果见图2。图2中除6、8和9三个样本外,其他训练后的样本和实测值具有很好的拟合性。

图2 FOA-SVM模型内腐蚀速率预测结果对比Fig.2 Comparison of corrosion rate prediction results of FOA-SVM model
3.3 FOA-SVM模型评价
为了体现FOA-SVM模型的优越性,使用徐州管道局输油管道试验数据对FOA-SVM模型进行检验,将其结果与灰色组合模型[4]、LS-SVM 模型[5]两种方法计算结果进行比较,见表2[17]。
由表2可见:FOA-SVM预测模型预测结果的方差和均差分别为0.037 4、1.397×10-3,从误差角度分析来看,FOA-SVM模型预测值方差、均差都小于其他算法,说明FOA-SVM模型具有相对较高的预测精度;从拟合效果来看,FOA-SVM模型的平方相关系数高于其他模型,说明FOA-SVM具有较好的拟合效果。
4 结论
(1)运用新建的FOA-SVM模型对输油管道内腐蚀速率进行了预测该模型预计的方差为1.397×10-3,均差为0.037 4,并与灰色组合模型、LS-SVM模型预测结果的对比分析,具有较好的泛化能力和较强的预测功能,可以相对准确、高效地对输油管道内腐蚀速率进行预测。
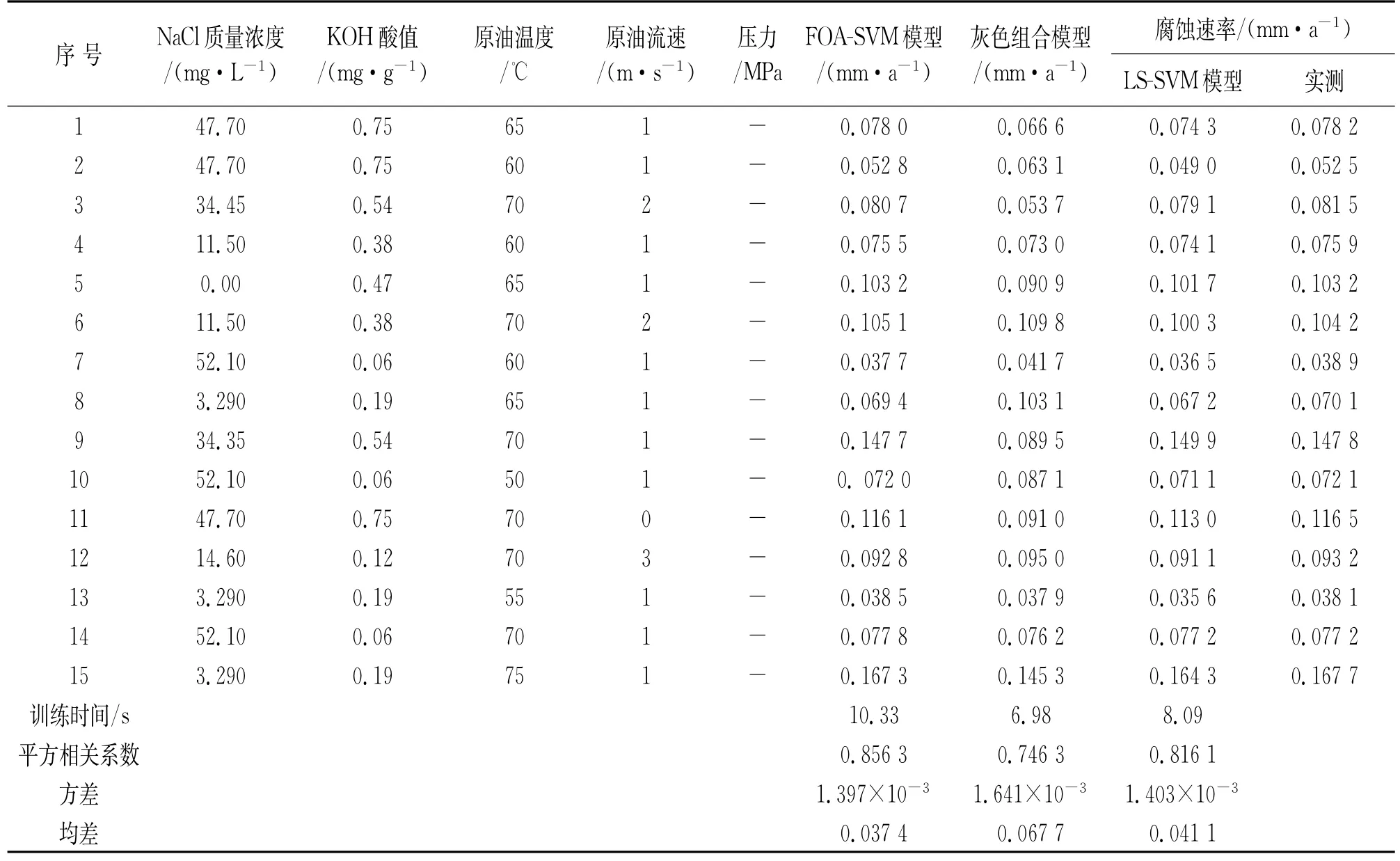
表2 模型预测结果对比表Tab.2 Comparison table of model evaluation performance
(2)FOA-SVM模型算法在输油管道内腐蚀速率预测的应用,充实了管道内腐蚀速率的预测方法,虽然能够准确、高效地预测管道内腐蚀速率,但该模型针对样本数目多时,存在训练消耗时间长、效率低的缺点,今后在预测效率问题上还需进一步研究。
[1] 陈浩力,吕仁军,姜炜,等.基于Excel的GM(1,1)模型在预测油气管道腐蚀速率中的应用[J].腐蚀与防护,2014,4:378-380.
[2] 孙海.天然气压气站内腐蚀挂片监测管道内腐蚀[J].腐蚀与防护,2011,3:239-242.
[3] 罗金恒,赵新伟,白真权,等.管道土壤腐蚀速率测试方法[J].油气储运,2004,11:50-53,60.
[4] 刘晓东,李著信.基于灰色组合模型的管道腐蚀速率预测[J].压力容器,2007(3):15-19.
[5] 王晓光,张弢,周慧.基于LS-SVM的管道腐蚀速率灰色组合预测模型[J].数学的实践与认识,2014(7):82-87.
[6] 黄天杰,殷安会,刘智勇,等.吉林油田矿场条件下CO2腐蚀模拟装置的建立及实验研究[J].表面技术,2015(3):69-73.
[7] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011(1):2-10.
[8] 顾亚祥,丁世飞.支持向量机研究进展[J].计算机科学,2011(2):14-17.
[9] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-43.
[10] PAN W.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-Based Systems,2011,26(7):69-74.
[11] 牛培峰,麻红波.基于支持向量机和果蝇优化算法的循环流化床锅炉Nox排放特性研究[J].动力工程学报,2013,33(4):267-271.
[12] 张宏伟,朱志洁,霍丙杰,等.基于改进的FOA-SVM导水裂隙带高度预测研究[J].中国安全科学学报,2013(10):9-14.
[13] 张勇,夏树发,唐冬生.果蝇优化算法对多峰函数求解性能的仿真研究[J].暨南大学学报(自然科学与医学版),2014(1):82-87.
[14] 宁剑平,王冰,李洪儒,等.递减步长果蝇优化算法及应用[J].深圳大学学报(理工版),2014(4):367-373.
[15] 王雪刚,邹早建.基于果蝇优化算法的支持向量机参数优化在船舶操纵预报中的应用[J].上海交通大学学报,2013(6):884-888.
[16] 高东磊,刘友宽,苏杰,等.果蝇优化算法和粒子群优化算法的应用对比[J].仪器仪表用户,2013(4):83-84,41.
[17] 裘冬平,孙建华.基于GA-BP神经网络的输油管道内腐蚀速率预测[J].青岛大学学报,2011,26(1):29-31.
Prediction of Oil Pipeline Internal Corrosion Rate Based on FOA-SVM model
WU Qingwei,WANG Jinlong,ZHANG Pin
(China Special Equipment Inspection and Research Institute,Beijing 100012,China)
TG179
A
1005-748X(2017)09-0732-05
10.11973/fsyfh-201709015
2016-02-25
吴庆伟(1986-),工程师,硕士,从事压力管道安全完整性技术研究与工程应用,13624181793,woqingweide@163.com
