灌溉诱发的黑方台黄土滑坡泥流机理分析*
2017-10-10赵纪飞黄嘉悦侯晓坤李同录蔺晓燕
赵纪飞,黄嘉悦,侯晓坤,李同录,蔺晓燕
(1.长安大学 地质工程与测绘学院,陕西 西安 710054; 2. 中国电建集团西北勘测设计研究院有限公司 陕西 西安 710054; 3. 中国有色金属工业西安勘察设计研究院,陕西 西安 710054; 4. 西安石油大学 地球科学与工程学院,陕西 西安 710065)
灌溉诱发的黑方台黄土滑坡泥流机理分析*
赵纪飞1,2,黄嘉悦3,侯晓坤1,李同录1,蔺晓燕4
(1.长安大学 地质工程与测绘学院,陕西 西安 710054; 2. 中国电建集团西北勘测设计研究院有限公司 陕西 西安 710054; 3. 中国有色金属工业西安勘察设计研究院,陕西 西安 710054; 4. 西安石油大学 地球科学与工程学院,陕西 西安 710065)
针对黑方台灌溉触发的黄土滑坡泥流,通过野外测量查明坡体地质结构,室内基本物理力学性质测测试、三轴试验和土水特征曲线的测试等,建立二维有限元渗流模型和弹塑性模型,分析灌溉条件下地下水位的变化特征和坡体的稳定性;并提取滑面上的应力状态分析其剪应力和抗剪强度的变化特点和屈服特征,结果表明该滑坡为纯黄土滑坡,黄土的饱和含水率高于液限,扰动易发生液化;黄土下层的粉质黏土层饱和渗透系数小,储水能力强,易积水形成潜水位。灌溉条件下,地下水位逐渐升高,边坡稳定性开始基本保持不变或缓慢降低,其快速降低始于水位开始接触滑面;灌溉前滑面上的抗剪强度均大于剪应力,随着灌溉进行,坡脚先发生屈服,且范围不断扩大,由于应力重分布作用,滑坡后缘也逐渐发生屈服,最终沿整个滑面上土体的剪应力均达到其抗剪强度。该滑坡为牵引式滑坡。
黄土滑坡;泥流;野外测量;室内试验;有限元模型;牵引式滑坡;甘肃黑方台
黄土地区为干旱半干旱气候,为了农业发展及人们生活需要,自1970年代以来,修建了大量的引水灌溉工程。这些工程对黄土地区的农业生产、经济发展发挥了重要的作用。但大量的引水灌溉不同程度的改变了灌区的自然地质条件,造成了灌区的生态破坏,从而引发了一系列滑坡灾害。甘肃黑方台是灌溉诱发的黄土滑坡、滑坡泥流最典型最集中的区域。该地区自1968年提水灌溉到1980年代初期方台村塬边开始出现滑坡以来,发生了许多大规模的滑坡和滑坡泥流,累积造成37人死亡,100多人受伤,并迫使4所小学搬迁等。对典型案例进行专门研究,查明其形成机理,对灾害预测、减少人民生命和财产损失,具有重要的科学意义和社会意义。
对黄土边坡破坏机理的研究有定性法和定量法。定性法是根据边坡破坏时的工程地质条件推断边坡破坏形式,如地下水位、水源、边坡几何形状等[1-2];或根据室内三轴或直剪试验得到的土样的应力应变特征进而推测边坡的破坏模式[3-4]。但这只是对边坡破坏机理的推测。定量法是采用极限平衡法、有限差分法等计算边坡稳定性。传统计算方法是建立在饱和土力学基础上的,采用饱和土的抗剪强度理论和强度参数。随着非饱和土力学的发展,非饱和土抗剪强度的建立,人们逐渐意识到水分入渗会引起基质吸力降低,使得土体的抗剪强度减小,边坡稳定性降低[5-8]。近年来,不断有学者采用考虑饱和非饱和渗透过程的数值分析方法研究入渗条件下边坡稳定性[9-12],该法考虑了水分入渗过程中坡体内基质吸力的降低及其对边坡稳定性的影响,一定程度上反映了边坡的破坏过程。但对边坡稳定性分析仍是采用的极限平衡法,只能得到边坡整体的稳定性,并未能反映滑面上抗剪强度和剪应力的变化情况。
综上所述,本文以甘肃黑方台一典型滑坡泥流为例,在查明坡体地质结构的基础上,取原状样进行基本物理力学指标的测试、三轴试验和土水特征曲线测试,并建立数值模型,进行饱和非饱和渗流分析和弹塑性有限元分析得到灌溉条件下边坡的水分场和应力场,在此基础上结合非饱和土的抗剪强度理论计算边坡的稳定系数,通过分析滑面上抗剪强度和剪应力的变化情况揭示边坡的变形破坏机理. 所用软件为Geo-studio。
1 理论介绍
非饱和渗流包括稳态渗流和瞬态渗流。利用质量守恒定律和达西定律,可得到渗流的控制方程(二维):
(1)
式中:kx(hm)、kz(hm)分别为x方向和竖直方向渗透系数;hm为基质吸力水头,其大小为ψ/g,ψ为基质吸力,g为重力加速度,ρ为水密度,θ为体积含水率,t为时间。
若式(1)右侧为0,为稳态渗流;若等式右侧不为0,则为瞬态渗流。非饱和渗流的控制方程中并未考虑土骨架变形,故该模型为非水力耦合模型。公式的求解需土水特征曲线、非饱和渗透系数、边界条件以及初始含水状态等。
非饱和渗流的不同时间步,通过弹塑性有限元分析可计算得到不同状态下坡体的应力场和应变场,进而分析其破坏机理。土体的本构模型可采用理想弹塑性模型,即破坏前土体为线弹性体,当应力达到其强度时,土体破坏。其中饱和区土体的强度由常用的莫尔库强度公式确定,见式(2);而非饱和土的抗剪强度公式目前主要有单变量强度理论(Bishop)和双变量强度理论,考虑到抗剪强度随饱和度的变化,Vanapalli 等[13], Oberg等[14], Khalili等[15]等提出利用土水特征曲线预测非饱和土的抗剪强度。由于本文的有限元计算是建立在非饱和渗流分析的基础上,开始计算时边坡的水分场已知,利用土水特征曲线预测非饱和土的抗剪强度简单易行,因此本文采用Vanapalli[13]提出的非饱和土强度公式进行计算,见式(3)。值得注意的是由于软件并没有专门计算非饱和区土体变形的本构模型,非饱和区土体也采用弹性理想塑形本构模型,但其弹性模量取值较饱和区弹性模量大。尽管这种计算不如采用非饱和本构模型计算结果准确,但其仍能反映出边坡应力场变化的一些重要特点(后面将会描述)。
τf=c’+σ’tanφ’;
(2)

(3)
式中:τf,为抗剪强度;c’,φ’为有效强度参数;σ’为有效应力;σ为总应力;ua为孔隙气压;uw为孔隙水压;(ua-uw)为基质吸力;θ为体积含水率;θs为饱和体积含水率;θr为残余体积含水率。
若破坏面已知,则根据滑面上的主应力和剪应力通过式(4)和式(5)可得到下滑力,跟据式(2)和式(3)强度理论可计算得到其抗剪强度[16]。以破坏面长度L为x轴,沿滑动面上的下滑力、抗剪强度为Y轴,绘制τf,τa曲线,通过分析曲线的变化特征,可阐明边坡的破坏过程;此外滑面上剪应力和抗剪强度积分的比值即为边坡的稳定系数[17-18],见式(6)。该计算方法无假设条件,其计算结果取决于有限元计算精度。将此计算结果同常用的极限平衡法的计算结果进行对比分析,以检验计算结果的准确性。

(4)

(5)

(6)
式中:σα,τα分别为滑动面上的正应力和剪应力;a为滑面倾角;xA和xB分别为剪入口和剪出口的横坐标;Fs为稳定系数。
2 室内试验及结果
本文所选案例为黑方台焦家一典型滑坡泥流,实测地质剖面如图1所示。该剖面土层厚度共52 m,其中0~24 m为Q3黄土,呈淡黄色,结构疏松多孔,具有垂直节理,即马兰黄土;24~44 m为Q2黄土,呈淡黄色,较致密,具有垂直节理;44~52 m为冲积粉质粘土,具有水平层理,呈棕红色,粘粒含量高,致密坚硬;该层之下为厚5 m的卵石层,磨圆度好,为黄河四级阶地堆积;卵石层之下为缓倾的白垩系紫红色砂泥岩,基岩产状为172°∠27°。滑坡发生时的地下水位埋深约34 m,位于Q2黄土层。而滑坡剪出口位于Q2黄土层中,距坡顶约45 m,为纯黄土滑坡。滑坡发生后,随即转化为泥流,顺开阔的坡面流下,形成坡面泥流,至坡脚处才停留堆积下来,水平滑距约280 m。分别在Q3黄土、Q2黄土和粉质黏土层中取土进行基本物理参数和土水特征曲线的测试。由于边坡破坏发生在黄土层中,故只对Q3和Q2黄土进行饱和三轴试验测得其强度参数,每层土的取样位置见图1。基本物理参数见表1,其中颗粒分析采用 Battersize 激光粒度仪测定,饱和渗透系数采用常规变水头渗透试验测定。由表1可知,Q3和Q2黄土的饱和含水率均大于液限,说明当土样受扰动时,亦发生液化。黄土的饱和渗透系数远远大于粉质粘土。

表1 Q3黄土、Q2黄土和粉质黏土层的基本物理性质参数

图1 黑方台焦家滑坡地质剖面图
2.1 三轴试验
本次试验所用试验仪器为南京土壤仪器厂生产的SLB-1型应力应变控制式三轴仪。试样直径6.18 cm, 高12.5 cm。按《土工试验规范》操作步骤将其试样安置在三轴仪的压力室后,先采用水头饱和法将土体内的大部分气体排出,此过程需要1~2 d,然后采用反压饱和的方法将土体饱和,反压为200 kPa,待孔压系数B>95%时饱和结束。之后打开排水阀门,分别将试样在100 kPa、200 kPa、300 kPa、400 kPa和500 kPa的围压下固结,待超孔隙水压力完全消散或消散95%时,固结结束。关闭排水阀门,开始剪切,剪切速率按规范要求设置为0.1mm/min。共10组试验。
图2和图3分别为Q3黄土和Q2黄土的三轴试验结果,从中可知两种黄土的应力应变关系曲线和总(有效)应力路径曲线等基本相似。从图2a和图3a中可知,土体的应力随应变的增大逐渐增大,基本表现出应变硬化或理想塑形的特征,仅图2a中400 kPa围压下的应力应变曲线有稍许软化特征。图2b和图3b分别为Q3和Q2黄土的(有效)应力路径曲线,取应变为20%的状态点为破坏点,绘制其(有效)破坏主应力迹线(Kf′)Kf线, 根据其倾角a和截距b,利用公式(7),可求得土体的有效抗剪强度参数和总强度参数。其中Q3黄土有效强度参数为c′=0.12 kPa,φ′=32.0°;总抗剪强度参数为c=0.15 kPa,φ=19.3°;Q2黄土的有效抗剪强度参数为c′=1.9 kPa,φ′=32.7°;总抗剪强度参数为c=0.7 kPa,φ=21.1°。对比可知,Q2和Q3黄土的抗剪强度参数大小接近。
(7)
2.2 土水特征曲线及非饱和渗透系数
采用张力计法测定Q2、Q3原状黄土和粉质粘土的土水特征曲线。所用张力计为浙江托普仪器公司生产的TEN型张力计,可测得的基质吸力的范围为0~100 kPa, 精度为2 kPa。 张力计使用前,采用真空饱和法将陶瓷头饱和。试验所用土样为大块正方体型原状样,边长约为30 cm,周围用塑料膜包裹严实防治水分散失。试验时将土样用同张力计直径相近的钻头打孔,孔底取样测定其质量含水率,清理孔隙中的散土后将充满水的张力计插入孔中,并用细沙填充孔隙后,将土样表层和张力计的接触部位密封,记录张力计读数直到读数基本稳定。此稳定值即为该土样在此含水率下的基质吸力。此时将张力计取出,土样洒水,密封至少10 d,之后重复上述操作步骤进行下一级基质吸力的测量。
上述测试方法只能得到一些离散的数据点,国内外学者提出多种数学模型反映非饱和土体基质吸力和体积含水率的关系曲线,常见的模型有Gardenr模型、Van Genuchten模型、Fredlund and Xing模型。

图2 Q3黄土三轴试验结果

图3 Q2黄土三轴试验结果
本文采用VG 模型[19](式8)对试验所测数据进行拟合,结果见图4,从中可知,相关系数均大于0.99,拟合效果较好。

(8)
式中:θw为体积含水率;θr为残余体积含水率;θs为饱和体积含水率;a、m、n为拟合参数,其中m=1-1/n。

图4 Q3黄土、Q2黄土和粉质黏土层的土水特征曲线
土体非饱和渗透系数的获得方法有直接法和间接法[20]。直接法是采用瞬态剖面法、稳态法等测试手段直接测量非饱和渗透系数。该法操作复杂,耗时长。间接法是土体的土水特征曲线法和相应的经验公式求取非饱和渗透系数。尽管预测结果和实测值稍有差异,但数量级大体相同,且可基本反映出非饱和渗透系数随饱和度的变化情况。考虑到试验成本问题,本文采用后者得到各层土体的非饱和渗透系数,采用VG模型[19](式9)计算得到的Q2、Q3黄土和粉质粘土的非饱和渗透系数见图5,从中可知Q3黄土的非饱和渗透系数最大,且黄土的非饱和渗透系数远远大于粉质粘土,这有利于水分在黄土中积聚。

图5 Q3 、Q2黄土和粉质粘土渗透系数函数曲线
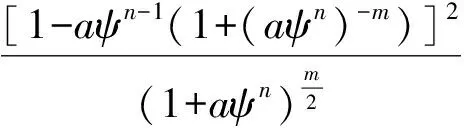
(9)
式中:kw为非饱和土的渗透系数;ks为饱和渗透系数;a、m、n为式9拟合参数。
3 滑坡破坏机理分析

图6 数值模型图
根据实测剖面建立计算模型(图6),土层自下而上分别为Q3黄土、Q2黄土,粉质粘土和第三系泥岩,其土层厚度依次为24 m、20 m和8 m。值得注意的是在边坡地质剖面(图1)中,粉质粘土下层为砂卵石层,考虑到其对上部边坡稳定性影响小,且厚度较薄,故将其省去。边坡的破坏面根据实测值确定(图1),剪出口设定在Q2黄土层底部,剪入口在坡顶。有限元网格尺寸设置为1 m,程序根据需要自动划分为三角形网格和四边形网格,共10 993个单元。由于Geo-studio软件的有限元求解采用增量法,故对渗流分析和弹塑性有限元分析均需设定其初始条件,即初始水分场和应力场。初始水分场通过年均降雨条件下的稳态渗流分析得到;初始应力场可由软件可自行计算获得。此外有限元的求解须知其边界条件,渗流分析的边界包括水头边界和流量边界,具体为地下水位的位置和地表灌溉的流量,此外还包括坡面为潜在渗流面(图6)。黑方台地区灌溉的地下水位位于粉质粘土层内,灌溉流量根据当地的实际灌溉量确定,据调查该区的灌溉主要分为春灌和冬灌,分别集中在5月份和11月份,灌溉流量为设置为16 mm/d,其他月份为停灌阶段,流量边界设置为0 mm/d。该渗流过程模拟了黑方台地区自1968年灌溉以来到1980年该区开始频繁出现滑坡期间的渗流过程,共12年。
弹塑性有限元计算所需的边界条件为位移边界条件,即边坡底部为固定端,各网格单元节点处没有横向位移和竖向位移,边坡左端各网格节点控制水平位移[16]。上述实验已获得非饱和渗流计算和弹塑性有限元计算的所需的土层参数,其中Q2,Q3黄土的弹性模量根据三轴试验的应力应变关系曲线,采用邓肯-张模型计算所得。此外由于Q3黄土区多为非饱和区,其弹性模量取值较饱和弹性模量大,根据渗流模拟结果计算得到该区的平均基质吸力,采用Oh & Vanapalli提出的非饱和区土弹性模量经验公式计算得到[21],见式(10)。由于粉质粘土和泥岩的性质参数对边坡应力场的计算结果影响不大,故其弹性模量和泊松比取经验值。具体参数见表2。
(10)
式中:E为弹性模量;Es为饱和弹性模量;(ua-uw)为基质吸力;sr为饱和度;a和k为拟合参数;对于IP为9.1的粉土其取值可分别为0.1,2。
图7为非饱和渗流分析计算结果,从中可知随着灌溉的进行,地下水位不断上升初始水位线位于粉质粘土层,经过2年的灌溉和停灌,水位线由初始的 26 m 上升到42 m,第6年水位达到Q2黄土上部,约50 m的位置,第12年的水位上升到52 m,达到了Q3黄土,穿越了滑带,在坡脚以泉水的形式溢出。图中 AB 线为从坡顶到粉质粘土底层的直线,自上而下每隔2 m设定一个点,共25个,读取每个点上的孔隙水压力,绘制成曲线如图8所示,从图8可知,随着水位线的上升,坡体饱和区土体的孔隙水压力压不断增大,而非饱和土土体的孔隙水压力在停灌阶段基本保持不变;在灌溉阶段,非饱和区上部负孔隙水压力会减小。总体上,随着灌溉过程的进行,饱和区不断增大,非饱和区出顶部5 m范围内的负孔隙水压不断增大缩小的波动外,其他部位的孔隙水压力基本维持恒定。根据式(3)非饱和土强度理论可知,土体的抗剪强度随基质吸力的减小而减小,当土体饱和时,若应力状态不变其抗剪强度最小。根据渗流分析结果和非饱和土抗剪强度理论可初步得到边坡的失稳主要同地下水位的上升有关,而这一现象将在后面稳定系数分析的结果中具体体现出来。
弹塑性有限元分析可得到边坡的应力场,通过提取不同灌溉年份时滑面上不同节点的应力状态(σx,σy,τxy),通过式(4)、(5)和式(2)或式(3)计算得到其剪应力和抗剪强度,以潜在滑面为x轴,以剪应力和抗剪强度为y轴,分析不同阶段剪应力和抗剪强度的变化特征。其中非饱和区的抗剪强度还需提取滑带上土体的基质吸力(ua-uw)。图9为不同阶段滑带上各节点的应力分布曲线,分别为灌溉前(a)、第3年10月停灌(b)、第8年5月灌溉(c)和第11年5月灌溉后剪应力和抗剪强度沿滑面上的分布。由图9a可以看出,初始状态下整个滑面上土体的抗剪强度均大于剪应力,边坡处于稳定状态。随着灌溉时间的增长以及土体中孔隙水压力的增大,土体的抗剪强度和剪应力都在不断地发生变化,抗剪强度不断地降低,由图9b可知灌溉第3年时,小范围的坡脚部位剪应力达到其抗剪强度,土体屈服.由图9c可以看出,当持续灌溉到第8年时,尽管边坡处于稳定状态,其安全系数为1.11(见图10),但坡脚处的土体仍然发生屈服,且屈服范围较第三年灌溉时大;此外滑坡后壁处也有部分土体屈服,这同应力重分布相关;当灌溉到第12年时,屈服范围又扩大,几乎整个滑面上土体的剪切应力到达了其抗剪强度,坡体失稳。从上述分析中不难看出,坡脚处的土体先屈服,坡脚失稳,该滑坡为牵引式滑坡。

表2 模型中所需各土层参数

图7 地下水位随灌溉的变化图

图8 参照线剖面上的孔隙水压力轮廓线

图9 不同阶段滑面节点抗剪强度和剪应力曲线

图10 稳定系数随灌溉时间变化曲线
将有限元渗流计算的渗流场耦合用于边坡稳定性计算,利用式(6)计算稳定系数,最终得出稳定系数随灌溉时间的关系曲线如图10所示。计算结果表明,随着地下水位的上升,滑坡的稳定系数降低,1970年11月灌溉后稳定系数突降,由初始1.34降到1.22,分析其原因,此时的地下水位由初始水位上升到了与粉质粘土层接触的水平滑带位置,粉质粘土层为相对隔水层,滑带土孔隙水压力开始上升,有效应力逐渐减小,土的抗剪强度降低。自1971年到1977年,稳定系数逐年降低,直到1980年5月灌溉之后,稳定系数达到1.01,该滑坡处于临界状态。计算结果同黑方台地区1980年开始出现大规模滑坡的实际状况相一致。
将此计算结果同常用的极限平衡法计算结果进行对比,见图11。其中极限平衡法所用软件为Geo-studio中的Slope模块,计算方法为M-P法,计算不需边界条件,所需材料参数为SWCC、容重、有效强度参数c’和φ’,具体见表2。通过对比分析可知,极限平衡法计算结果和本文有限元法的计算结果不尽相同,但差异较小,其相关系数为0.99。

图11 稳定系数计算结果对比图
4 结论
通过野外剖面测量,室内试验,和数值模拟等手段,结合非饱和土力学理论研究了甘肃黑方台一滑坡泥流的失稳机制,并得到以下结论:
(1) 该滑坡为纯黄土滑坡,坡体前缘有广阔的临空面。黄土的饱和含水率大于液限,扰动时易发生液化;黄土层下的粉质粘土层饱和渗透系数小,储水能力强,有利于水分积聚,形成潜水位。
(2) 该地区自1967年灌溉以来,地下水位不断上升,非饱和区的基质吸力变化不大。结合非饱和土强度理论,边坡稳定性的降低主要同地下水位上升相关,其稳定系数的快速下降始于地下水位开始接触潜在滑面。
(3) 剪应力和抗剪强度的对比分析结果表明,滑面上初始边坡的抗剪强度均高于剪应力,随着地下水位的上升,坡脚土体先屈服,且屈服范围不断扩大;由于应力重分布,滑坡后缘的土体也逐渐屈服。该滑坡为牵引式滑坡。
(4) 野外调查中若在黄土层中发现泉流等地下水排泄口,表明地下水位已上升到黄土层内部,边坡处于欠稳定状态,应及时做好防范措施,如距离坡面一定范围内设置为危险区、及时迁移相关农户等。
[1] 雷祥义. 陕西泾阳南缘黄土滑坡灾害与引水灌溉的关系[J]. 工程地质学报, 1994, 3(1): 56- 64.
[2] 王家鼎. 高速黄土滑坡一种机理—饱和黄土蠕动液化[J].地质评论, 1992, 38(6): 532-539.
[3] 戴福初,陈守义,李焯芬. 从土的应力应变特性探讨滑坡发生机理[J]. 岩土工程学报, 2000, 22(1):127-130.
[4] 金艳丽, 戴福初. 灌溉诱发黄土滑坡机理研究[J]. 岩土工程学报, 2007,29(10): 1493-1499.
[5] Fredlund D G and Rahardjo H. Soil Mechanics for Unsaturated Soils[M].Wiley, New York, NY, USA,1993.
[6] Brand E W. Some thoughts on rainfall-induced slope failures[C]// Proc of 10th Int Conf on Soil Mech and Found Eng, Brookfield, 1981:373-376.
[7] Lee L M, Gofar N and Rahardjo H. A simple model for preliminary evaluation of rainfall-induced slope instability[J]. Engineering Geology ,2009,108(3/4): 272-285.
[8] 简文星,许强,童龙云,等.三峡库区黄土坡滑坡降雨入渗模型研究[J]. 岩土力学, 2013, 34(1): 3527-3535.
[9] 金艳丽, 戴福初. 地下水位上升下黄土斜坡稳定性分析[J]. 工程地质学报, 2007,15(5): 599-606.
[10] 朱立锋, 胡炜, 贾俊,等.甘肃永靖黑方台地区灌溉诱发型滑坡发育特征及力学机制[J].地质通报, 2013, 32(6): 840-846.
[11] 谷天峰, 朱立峰, 胡炜,等.灌溉引起地下水位上升对斜坡稳定性的影响[J]. 现代地质, 2015, 29(2): 408-415.
[12] 董英, 贾俊, 张茂省,等.甘肃永靖黑方台地区灌溉诱发作用与黄土滑坡响应[J]. 地质通报, 2013, 32(6): 893-898.
[13] Vanapalli S K,D G Fredlund,D E Pufahl,et al. Model for the prediction of shear strength with respect to soil suction[J] .Canadian Geotechnical Journal ,1996,33(3): 379-392.
[14] Khalili N,Khabbaz M H. A unique relationship for the determination of the shear strength of unsaturated soils[J]. Gotechnique,1998,48(5):681-687.
[15] Oberg A, Sallfors G. Determination of shear strength parameters of unsaturated silts and sands based on the water retention curve[J]. Geotech Test J GTJODJ ,1997,20(1):40-48.
[16] GeoSlope International Ltd. Sigma/W user’s guide for stress-deformation analysis[R]. Calgary, Alta: GEO-SLOPE International Ltd; 2007.
[17] 张常亮, 王阿丹, 邢鲜丽,等.侵蚀作用诱发黄土滑坡的机制研究[J].岩土力学,2012, 33(5): 1585-1592.
[18] 侯晓坤,李同录,李萍. 开挖黄土高边坡的应力路径及变形破坏机制分析[J]. 岩土力学 ,2014,35(S2):558-556
[19] Van Genuchten,M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980,44(5):892-898.
[20] 王红. 非饱和黄土渗透性函数的试验研究[D]. 西安:长安大学,2015.
[21] Vanapalli Sai and Won Oh.A model for predicting the modulus of elasticity of unsaturated soils using the soil-water characteristic curve[J]. International Journal of Geotechnical Engineering, 2010, 4(4): 425-433.
Abstract:For a loess flow slide in Heifangtai Gansu Province, field investigation for the geological structure, laboratory tests including basic physical parameters tests, traixial tests, SWCC tests, and finite seep and elastic-plastic numerical model are conducted to study the failure mechanism.The changing characters of groundwater table and the related slope stability are analyzed. The yield characteristics associated by comparing the shear stress and shear strength along the slide surface are studied by extracting the stress state along the failure surface. Results show that the flow-slide is a loess landslide, whose failure surface lies in the loess layer. The saturated water content of loess is higher than its liquid limit, meaning the loess is easy to liquefy when it is disturbed; the silt clay below the loess layer has a low saturated permeability and high water storage capacity, making it easy to form a water table above it. Under the irrigation conditions, the ground water table increases slowly, the factor of safety of the slope fluctuates at first and begin to decrease greatly when the groundwater table researches the slide surface. Before irrigation, the shear strength is higher than the shear strength along the slide surface. With the irrigation continuing, the slope toe yields first, and the yield area expands upwards. The following stress redistribution leads to the yield of soil at the crest of slope. At the end the whole soil along the slide surface yields with the stress researches the shear strength. The landslide is a retrogressive landslide.
Key words:loess flow-slide; field investigation; laboratory tests; finite numerical model; retrogressive landslide
Analysis of a Flow-slide in Heifangtai Induced by Irrigation
ZHAO Jifei1, 2, HUANG Jiayue3, HOU Xiaokun1, LI Tonglu1and LIN Xiaoyan4
(1.SchoolofGeologicalEngineeringandSurveying,Chang’anUniversity,Xi’an710054,China; 2.NorthwestEngineeringCorporationLimited,Xi’an710054,China; 3.Xi’anEngineeringandDesignResearchofChina,Xi’an710054,China;4.SchoolofEarthScienceandEngineering,Xi’anShiyouUniversity,Xi’an710065,China)
赵纪飞,黄嘉悦,侯晓坤,等. 灌溉诱发的黑方台黄土滑坡泥流机理分析[J]. 灾害学,2017,32(4):60-66. [ZHAO Jifei, HUANG Jiayue, HOU Xiaokun,et al. Analysis of a Flow-slide in Heifangtai Induced by Irrigation[J]. Journal of Catastrophology,2017,32(4):60-66.
10.3969/j.issn.1000-811X.2017.04.010.]
X43;P642.131
A
1000-811X(2017)04-0060-07
2017-02-07
2017-04-17
国家自然科学基金项目(40772181, 41372329);国家重点基础研究发展计划(973计划)资助项目(2014CB744701)
赵纪飞(1987-),男,山东日照人,博士研究生,工程师,主要从事边坡工程方面的研究. E-mail:523327087@qq.com
10.3969/j.issn.1000-811X.2017.04.010
