基于SPI的塔里木河流域干旱识别及演变趋势

魏光辉，刘新华，马 亮

(1.新疆塔里木河流域管理局，新疆 库尔勒 841000；2.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052)

基于SPI的塔里木河流域干旱识别及演变趋势

魏光辉1，刘新华1，马 亮2

(1.新疆塔里木河流域管理局，新疆 库尔勒 841000；2.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052)

根据塔里木河流域1961—2010年的逐月降水资料，利用SPI指标，结合主成分法、谐波法研究了干旱时空演变特征，结果表明：对不同尺度的SPI提取主成分，其累积方差贡献率均可达到70%左右，且采用因子载荷来划分流域干旱空间分布是可行的；塔里木河干流上中游干旱具有8.2a的波动周期，未来将处于一个由偏枯逐渐向正常转变的阶段；和田河流域存在5.4a的波动周期，未来将处于一个由正常逐渐向干旱转变的阶段；开都—孔雀河流域具有3.5a波动周期，未来将处于一个由正常逐渐向偏丰转变的阶段；叶尔羌河流域变化无序，无明显的波动周期.

干旱；SPI；主成分分析；谐波分析；塔里木河流域

我国是农业大国，气象干旱长期困扰着农业生产.据报道，我国每年受旱面积约21.593万km2，其中气象干旱约占60%，直接粮食损失约100亿kg[1].随着经济社会的迅速发展，全球气候变暖趋势将导致干旱进一步加重，从而对国民经济及群众生活造成严重影响.目前，在干旱研究方面，以标准化降水指数(standard precipitation index，SPI)为代表的气象干旱指标由于具备资料获取容易、计算简单、能较好地反映多时间尺度干旱强度和有效地表征区域干旱的程度和持续时间，故而广泛应用于世界各地[2-5].

塔里木河流域位于新疆南部，该地区降水稀少，蒸发强烈，生态环境极度脆弱，“绿洲经济，灌溉农业”是其显著特点，干旱是绿洲灌溉农业最大的威胁.已有文献鲜有报道基于气象干旱指数法的该流域干旱演化特征研究.鉴于此，本文以塔里木河流域为研究区，根据流域内17个典型气象站1961—2010年的逐月降水量数据，采用SPI指数，分析研究区干旱演化趋势，以期为流域抗旱减灾提供参考.

1 计算方法

1.1 标准化降水指数

气象干旱指某一地区内长期缺乏降水，水分支出大于水分收入而造成的水分短缺现象.标准化降水指数(SPI)能够较好地反映干旱强度和干旱历时，时空适用性较强[6].其基本原理如下：

(1)

(2)

式中：α—形状参数；β—尺度参数；x—降雨量/mm；Γ(α)—gamma函数.

采用极大似然估计方法求解α、β，即：

(3)

(4)

(5)

式中：n—计算序列的长度.

H(x)=q+(1-q)G(x)

(6)

式中：q—降雨序列中0值出现的频率；G(x)—累积概率密度函数；H(x)—累积概率.

用高斯函数将H(x)标准化后得到最终的SPI值，其干旱等级[7](见表1).

表1 SPI干旱等级划分标准

1.2 主成分分析法

主成分分析法的原理是通过线性组合的方式对处于时间i的p个原始变量Xi,1，Xi,2，…，Xi,p，生成p个主成分Yi,1，Yi,2，…，Yi,p，构成以下方程组：

(7)

式中，Y变量之间具有正交且互不相关的特性，Yi,1解释了原始变量总方差的主要部分；Yi,2解释剩余方差的主要部分.线性方程组里的系数为主成分与变量之间的相关系数.

(1)由于SPI的计算过程包含标准化，故可直接采用SPI序列进行主成分提取.

(2)主成分可以通过方差、协方差、相关系数矩阵进行提取，本研究采用相关系数矩阵R=(rij)p×p.

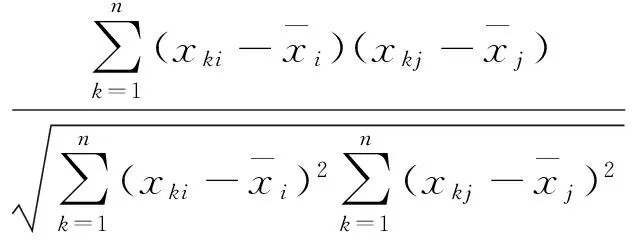
(8)

根据特征方程|λI-R|=0计算特征值并按λ1≥λ2≥…,≥λp≥0排列，然后求出相应的特征向量.

(3)计算贡献率及累积贡献率

贡献率em为：

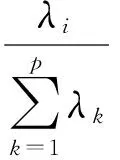
(9)

累计贡献率Em为：

(10)

取累计贡献率达70%左右为主成分.

(4)计算主成分载荷

(11)

(5)为更清楚地展现各主成分与原始变量之间的关系，采用最大变异法进行因子旋转，该方法使因素轴间夹角保持90°(即两因素间不相关)，通过V最大化来实现，计算式为：

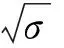
(12)

式中：σ—每个主成分对应载荷的标准差.

旋转后的主成分与原始变量之间得到更高的相关系数，使聚类后的原始变量具有最相似的时变特征.

1.3 谐波分析法

对于时间序列xt(t=1,2,…,n)，当满足一定条件时，可通过傅立叶级数展开：

(13)

或

(14)

式中：i—波数；l—谐波总个数.

(15)

序列xi的第i个谐波表示为：

aicosωit+bisinωit=Aicos(ωit+θi)

(16)

它的频谱值为：

(17)

为判断序列周期，需要对功率谱进行周期的显著性检验.本文根据Fisher判据来判断，基本步骤如下[8-9]：

令

(18)

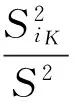
(19)

式中：r—满足1-(r+1)YK>0的最大整数.

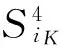
2 结果分析

2.1 气象干旱空间分布

塔里木河流域涉及范围广，干旱事件的识别应充分考虑流域下垫面和水文气象条件的空间变异性，因此需要对研究区进行干旱分区.本研究采用主成分分析法对流域干旱分区，考虑到流域降雨稀少、蒸发强烈，无雨月数占很大比例.因此选取SPI-3、SPI-6作为流域气象干旱评价指标.其中SPI-3表示3个月的降水SPI值，以反映短期气象干旱的特征，即降水季节性的变化；SPI-6表示6个月的降水SPI值，反映中长时期的降水状况.

对于不同尺度的气象干旱指标SPI，采用上述方法分别提取了各自的主成分，它们对累积方差贡献率均可达到70%左右(见图1).

图1 不同尺度SPI的主成分方差贡献率

载荷表示各主成分与原始变量的相关系数，与同一主成分相关系数高的变量得以聚类.因此采用因子载荷来划分塔河流域气象干旱空间分布(见图2).图2表明，通过SPI进行流域干旱分区是可行的.

2.2 气象干旱影响范围

研究区受春旱影响严重，以SPI-33-5月表示春季3～5月份的累积降雨量丰枯情况，通过主成分分析法提取出SPI-33-5月序列的4个主成分，其中第1主成分能够代表干流上中游的春季旱涝情况；第2主成分能够代表和田河流域春季的旱涝程度；第3主成分表示开都—孔雀河流域春季旱涝程度；第4主成分代表叶尔羌河流域春季旱涝情况(见图3).

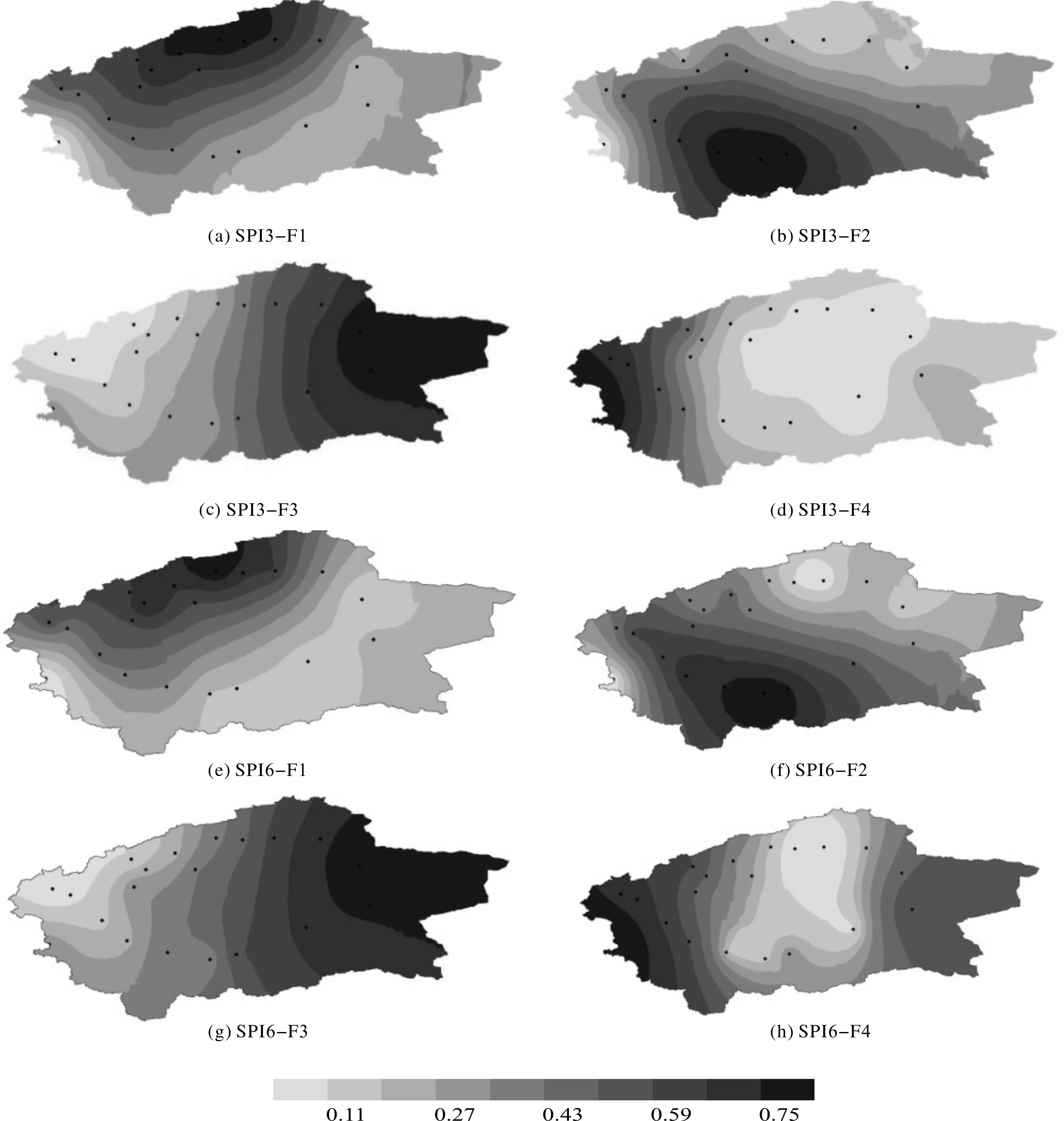
图2 不同尺度SPI因子载荷空间分布

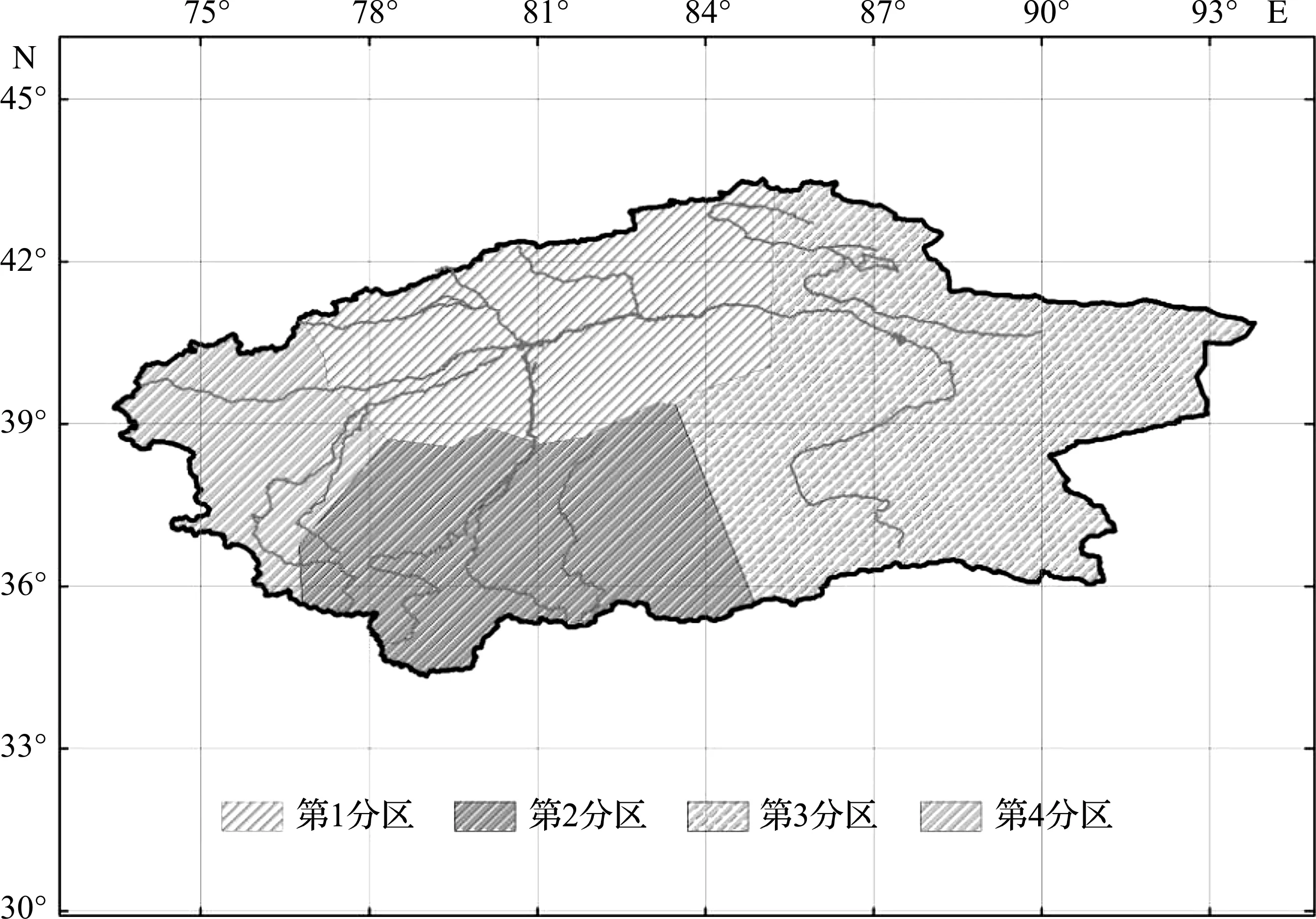
图3 基于SPI-33-5月塔河流域干旱分区

依据各主成分范围内的气象站点分布，采用泰森多边形进行划分，得到各气象站点的面积权重，统计各主成分区域春旱事件的影响范围，结果表明：第1分区进入2007年以后春旱事件的影响范围达到了100%，以轻度干旱、中度干旱、重度干旱为主，春旱形势严峻；第2分区2007年之后春旱的影响范围明显减小，但相应的干旱程度越发严重，以中度干旱和重度干旱的形式出现；第3分区2002年之后春旱形势略有缓和，以轻度干旱的形式出现；第4分区2005年之后春旱程度加重，影响范围趋于平稳，在2007年出现过一次极端干旱事件.综上所述，塔河流域各干旱分区，发生的春旱事件在时间、影响范围和程度上差异显著(见图4).

图4 各分区干旱影响范围变化

2.3 气象干旱演变趋势

采用谐波分析法对SPI-33-5月的4个主成分进行周期识别，以诊断流域各分区范围内春季的旱涝演变规律.结果表明：SPI3-5月-F1具有8.2a的波动周期.SPI3-5月-F2存在5.4a的周期成份，SPI3-5月-F3具有3.5a变化周期，SPI3-5月-F4变化无序，无明显的波动周期.通过主震荡周期可以预测：干流上中游未来将处于一个由偏枯逐渐向正常转变的阶段，和田河流域将处于一个由正常逐渐向干旱转变的阶段，开都—孔雀河将处于一个由正常逐渐向偏丰转变的阶段(见图5).

对于气象干旱，通过主震荡周期分析可以进行预测(见图6).流域西北部(第1主成分区域)未来将处于一个由偏枯逐渐向正常转变的阶段，流域西南部(第2主成分区域)处于一个由正常逐渐向干旱转变的阶段，流域东部(第3主成分区域)处于一个由正常逐渐向偏丰转变的阶段，流域西部(第4主成分区域)处于一个由偏枯逐渐向正常转变的阶段.

图5 SPI3～5月主成分周期性分析

图6 流域主成分周期性分析

3 结 论

(1)对于不同尺度的气象干旱指标SPI，分别提取各自的主成分，它们对累积方差贡献率均可达到70%左右；采用因子载荷来划分流域气象干旱空间分布是可行的.

(2)通过主成分分析法提取春旱区域，其中第1主成分能够代表干流上中游的春旱程度，第2主成分能够代表和田河流域春旱程度，第3主成分可代表开都—孔雀河流域春旱程度，第4主成分代表叶尔羌河流域春旱程度.

(3)谐波分析结果表明，塔里木河流域干流上中游干旱具有8.2a的波动周期，未来将处于一个由偏枯逐渐向正常转变的阶段；和田河流域存在5.4a的周期成份，未来将处于一个由正常逐渐向干旱转变的阶段；开都—孔雀河流域具有3.5a变化周期，未来将处于一个由正常逐渐向偏丰转变的阶段；叶尔羌河流域变化无序，无明显的波动周期.

[1] 袁文平,周广胜.标准化降水指数与Z指数在我国应用的对比分析[J].植物生态学报,2004,28(4):523-529.

[2] 杨 庆,李明星,郑子彦.7种气象干旱指数的中国区域适应性[J].中国科学:地球科学,2017，47(3):337-353.

[3] 徐 羽,许有鹏.近50年重庆市气象干旱时空分布特征研究[J].水土保持研究,2016，23(6):363-368.

[4] 吴 琼,赵春雨.1951-2014年辽宁省气象干旱时空特征分析[J].干旱区资源与环境,2016，30(3):151-157.

[5] 卢文喜,安永凯.吉林西部季节性气象干旱的时空演化特征[J].吉林大学学报：地球科学版,2016，46(2):543-551.

[6] 李永坤,丁晓洁.北京市降水量变化特征分析[J].北京水务,2013(2):9-12.

[7] 栗 健,岳耀杰,潘红梅.中国1961—2010年气象干旱的时空规律——基于SPEI和Intensity analysis方法的研究[J].灾害学,2014(4):176-182.

[8] 付丽娟,曹 杰,德勒格日玛.三种气象干旱指标在内蒙古地区的适用性分析[J].干旱区资源与环境,2013，27(2):108-113.

[9] 张调风,张 勃,王有恒.基于综合气象干旱指数的石羊河流域近50年气象干旱特征分析[J].生态学报,2013，33(3):975-984.

Drought Identification and Evolution Trend of Tarim Basin Based on SPI

WEI Guang-hui1, LIU Xin-hua1, MA Liang2

(1.Xinjiang Tarim Basin Management Bureau, Korla 841000, China; 2.College of Water Conservancy and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052, China)

Based on the monthly precipitation data during 1961—2010, by SPI index, the temporal and spatial evolution of drought is studied combined with principal component analysis and the harmonic method, and the results showed that extracting principal component on different scales of SPI, the cumulative variance contribution rate can reach to 70%, and the space distribution of the basin drought by factor loading is feasible: the drought in upper and middle reaches of the Tarim River has fluctuation period of 8.2a, with the stage from low gradually to normal transition in the future; while the fluctuation period of 5.4a in Hotan Basin with the stage from normal gradually to drought transition, and Kaidu-Kongque Basin has 3.5a cycle in the future, with a normal transition gradually to rich stage; the Yarkant Basin changes unordered with no obvious fluctuations. The research can provide scientific reference for agriculture drought resisting in Tarim Basin.

drought; SPI; principal component analysis; harmonic analysis; Tarim Basin

TV131

A

1008-536X(2017)03-0041-06

2016-10-19

水利部公益性行业科研专项基金资助项目(201501059)；新疆塔里木河流域阿克苏典型灌区地下水资源调控研究基金资助项目(TGJAKS-SKS-2015-002)

魏光辉(1981-)，男，新疆石河子人，博士，高级工程师，主要从事干旱区水资源利用研究.