快递与第三方智能快递柜合作机制的演化博弈分析
2017-10-10李玉民王新露
李玉民, 杨 露, 王新露
(郑州大学 管理工程学院,河南 郑州 450001)
快递与第三方智能快递柜合作机制的演化博弈分析
李玉民, 杨 露, 王新露
(郑州大学 管理工程学院,河南 郑州 450001)
智能快递柜在一定程度上解决了快递的末端配送问题.首先,基于演化博弈理论构建了快递企业与第三方智能快递柜企业间的演化博弈模型;然后,研究了系统的动态演化过程,分析了二者合作的影响因素;最后,用Matlab进行算例分析.研究结果表明:当总超额收益大于合作总成本时,二者才有开展合作的可能;合作概率与超额收益正相关,与合作成本负相关;存在一个最佳的超额收益分配比例,使得合作概率最大;合理的收益分配机制与成本分担机制有利于二者建立合作关系,实现互利共赢.
末端物流;合作机制;演化博弈;智能快递柜;快递企业
0 引言
国家邮政局最新数据显示,2016年全年快递服务企业业务量为312.8亿件,同比增长51.3%[1].快递量的爆炸式增长给传统的快递配送模式带来了巨大的挑战,尤其是在“最后一百米”送达环节,车辆停靠、通行难,快递进校园、进社区难等突出问题在一定程度上影响并制约着快递企业的服务质量.基于此背景,智能快递柜应运而生.目前国内智能快递柜主要有三种运营模式:快递企业自建自用、电商企业自建自用及第三方平台共用型,其中应用最广泛的是第三种,即由第三方负责快递柜的运营,为若干快递企业和客户群体提供服务.因此,为了充分发挥智能快递柜的优势,有效解决“最后一百米”送达难题,快递企业与第三方智能快递柜企业应建立良好的合作伙伴关系.
由于我国快递行业起步晚、发展时间短,国内的研究主要集中在快递企业的服务质量、客户满意度、市场竞争力以及网点选址[2-4]等方面.智能快递柜在国内出现的历史很短,学者对此的研究较少,多是从分析智能快递柜的发展现状入手,简单论述现阶段存在的问题[5-6].鲜有学者对快递企业与第三方智能快递柜企业间的合作进行研究.鉴于此,笔者将运用演化博弈理论,对有限理性的快递企业与第三方智能快递柜企业的博弈行为进行研究,分析二者合作的影响因素,探讨有利于合作的收益分配机制及合作成本分担机制,为二者建立合作关系提供理论参考.
1 演化博弈模型的构建
演化博弈理论以生物进化论、种群动力学以及遗传基因理论为思想基础,从有限理性角度出发,对群体间的竞合关系进行研究[7].
1.1 基本假设
(1)快递企业与第三方智能快递柜企业对市场信息的识别判断、分析推理能力不同,对决策结果无法完全预测,很难确定何种决策能使自身利益最大化.所以,双方均可能采取合作、不合作两种策略,需要进行多次博弈,不断调整并改进策略,才能达到纳什均衡.因此本研究建立假设H1:快递企业采取合作策略的概率是x,不合作策略的概率是(1-x);第三方智能快递柜企业采取合作策略的概率是y,不合作策略的概率是(1-y);0≤x,y≤1.
(2)快递企业独立经营时,采用传统方式收发快递实现盈利.第三方智能快递柜企业也可独立经营实现盈利,比如,可通过智能终端设备提供自助业务、通过智能柜提供学校及社区周边生活消费品自取服务、通过APP推送服务信息向商家收取广告费等.因此本研究建立假设H2:快递企业与第三方智能快递柜企业采取不合作策略,即二者独立经营时的正常收益分别为π1和π2;π1、π2>0.
(3)快递企业与第三方智能快递柜企业进行合作,各快递企业由独立分散经营走向整合集约化管理,会产生一定超额收益.因此本研究建立假设H3:若快递企业和第三方智能快递柜企业合作,将会给整个系统带来超额收益Δπ,快递企业的超额收益分配比例为a,第三方智能快递柜企业的分配比例为(1-a);Δπ>0,0 (4)快递企业与第三方智能快递柜企业合作的成本不仅包括场地租金、装修费及快递柜的采购费等,还包括为达成合作,前期谈判产生的交通费、通讯费等;总合作成本由快递企业与第三方智能快递柜企业按照一定比例共同承担.当一方倾向合作时,无论另一方合作与否,倾向合作一方均会为促成合作而努力,势必产生一定的前期投入,比如积极主动地谈判、租赁装修场地等.故无论合作是否达成,快递企业与第三方智能快递柜企业仍需付出一定的成本.因此本研究建立假设H4:快递企业与第三方智能快递柜企业的合作成本为C,快递企业的分担比例为b,第三方智能快递柜企业的分担比例为(1-b);C>0,0 根据演化博弈论的思想建立快递企业与第三方智能快递柜企业演化博弈的支付矩阵[8],见表1. 根据博弈双方的支付矩阵,可得快递企业选择合作策略的期望收益为: E1c=y(π1+aΔπ-bC)+(1-y)(π1-bC). (1) 表1 博弈双方的支付矩阵 快递企业选择不合作策略的期望收益为: E1u=yπ1+(1-y)π1. (2) 所以,快递企业的平均期望收益为: E1=xE1c+(1-x)E1u=x(ayΔπ-bC)+π1. (3) 根据演化博弈理论,可得快递企业采取合作策略的复制动态方程为[9]: =x(1-x)(ayΔπ-bC). (4) 同理,第三方智能快递柜企业采取合作策略的复制动态方程为: (5) 令F(x)=0,F(y)=0,可知博弈系统在平面S={(x,y);0≤x,y≤1}内有5个局部均衡点,分别为:O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(m,n),其中m=(1-b)C/(1-a)Δπ,n=bC/aΔπ. 根据二者的复制动态,可得复制动态方程的雅克比矩阵为: (6) 则 (7) 矩阵J的迹为: Tr(J)= (1-2x)(aΔπy-bC)+ (1-2y)[(1-a)Δπx-(1-b)C]. (8) 根据雅可比矩阵可以判断均衡点的局部稳定性[8],分析结果如下: 当aΔπ 由表2可知,当aΔπ 表2 3种情况下均衡点的局部稳定性分析结果 图分别如图1所示,从中可以看出,无论初始状态位于平面S的任何位置,系统最终都收敛于点O,即快递企业和第三方智能快递柜企业中只要有一方的超额收益小于其合作成本,演化稳定策略就一定是双方互不合作. 图1 演化博弈动态相位图Fig.1 The dynamic phase diagram of the evolutionary game 当aΔπ>bC,(1-a)Δπ>(1-b)C,即快递企业和第三方智能快递柜企业采取合作策略各自获得的超额收益均大于其付出的合作成本时,有5个均衡点,它们的局部稳定性分析结果见表3. 表3 aΔπ>bC,(1-a)Δπ>(1-b)C时均衡点的局部稳定性分析结果 由表3可知,点O和C是稳定的,是演化稳定策略,点A和B是不稳定的,点D是鞍点.其中,稳定点O对应于快递企业与第三方智能快递柜企业二者都采取不合作策略,稳定点C对应于二者合作. 由于国内智能快递柜的发展处于初级阶段,快递企业与第三方智能快递柜企业的演化博弈还需一段时间,所以该阶段的博弈过程中,系统会保持合作与不合作两种策略并存的状态,最终将演化到哪个均衡点取决于初始状态的位置.当aΔπ>bC,(1-a)Δπ>(1-b)C时演化博弈动态相位图如图1(d)所示,由不稳定点A、B和鞍点D连接而成的折线将平面S分为两个区域.当初始状态位于区域OADB时,系统将收敛于点O,即快递企业与第三方智能快递柜企业都选择不合作;当初始状态位于区域ADBC时,系统将收敛于点C,即二者选择合作. 综上,只有快递企业和第三方智能快递柜企业各自的超额收益均大于其合作成本时,系统才可能演化为相互合作的状态;任何一方的超额收益小于其合作成本时,系统将收敛于点O(0,0),即双方互不合作. 由上述分析可知,快递企业和第三方智能快递柜企业获得的超额收益均大于其合作成本时,演化稳定策略有两种:(合作,合作)与(不合作,不合作).由表1可知,双方合作可使各自收益最大化,所以从长远角度看,双方都希望通过相互合作谋求自身利益的最大化.而系统的演化路径及最终的演化结果与博弈双方的初始状态、支付矩阵的相关参数有关. 由图1(d)可知,系统向(合作,合作)与(不合作,不合作)两种稳定策略演化的概率分别取决于四边形OADB与ADBC的面积,所以可通过分析四边形面积的影响因素,来分析各参数对系统演化路径及演化结果的影响[10].根据图1(d)可得 SADBC=SΔADC+SΔBCD (9) 结论1:快递企业和第三方智能快递柜企业选择合作策略支出的成本C越小,二者合作的概率越大. 证明1:对SADBC求关于C的一阶偏导: (10) 所以,SADBC是C的单调减函数,双方选择合作策略付出的成本C越小,折线上方区域ADBC的面积越大,系统收敛于稳定点C的概率也就越大,即双方采取合作策略的概率越大. 结论2:快递企业和第三方智能快递柜企业合作的超额收益Δπ越大,二者采取合作策略的概率越大. 证明2:对SADBC求关于Δπ的一阶偏导: (11) 因此,SADBC是Δπ的单调增函数,Δπ越大,折线上方区域ADBC的面积越大,系统收敛于稳定点C的概率就越大,即双方采取合作策略的概率越大. 结论3:存在一个最佳的超额收益分配比例a,使得双方采取合作策略的概率最大. 证明3:对SADBC求关于a的一阶偏导: (12) 再对SADBC求关于a的二阶偏导: (13) 由此可知,在区间(0,1)存在一个a使SADBC取得极大值,即存在一个a使系统收敛于稳定点C的概率最大. 结论4:快递企业与第三方智能快递柜企业对超额收益的分配比例与对合作成本的承担比例正相关时,双方采取合作策略的概率增大. 证明4:对SADBC求关于b的一阶偏导: (14) 当a>1-a时,SADBC与b正相关,当b增大时,SADBC增大,系统收敛于点C的概率增大,说明当快递企业获得的超额收益份额多于第三方智能快递柜企业时,此时即使快递企业承担的合作成本增加,快递企业依然会坚持合作,双方仍会达成合作. 综上,当快递企业与第三方智能快递柜企业对超额收益的分配比例与合作成本的承担比例正相关时,双方才觉得公平,系统才能最终演化为相互合作状态. 根据国内某高校智能快递柜的实际运营状况,结合模型的假设条件,设快递企业与第三方智能快递柜企业的合作成本C∈[1 500,3 000]万元,成本分担系数b∈[0.1,0.9],合作的超额收益Δπ∈[5 000,10 000]万元,超额收益的分配系数a∈[0.1,0.9]. 当参数值给定时相关参数的取值如下:C=2 000万元,b=0.3,Δπ=8 000万元,a=0.4.根据上述参数的取值,运用Matlab软件进行算例分析,验证结论有效且可行[11]. 设合作成本C∈[1 500,3 000]万元,超额收益Δπ∈[5 000,10 000]万元,其他参数取值如上文所述,研究此时SADBC的变化趋势,如图2所示. 图2 C和Δπ对合作概率的影响Fig.2 The effect of C and Δπ on cooperation probability 由图2可知,SADBC随着合作成本C的增大而减小.由此表明:快递企业与第三方智能快递柜企业的合作成本越大,资金风险越大,一定程度上挫伤了合作积极性,使得合作的概率减小;SADBC随着超额收益Δπ的增大而增大,即合作的超额收益越大,双方合作的概率越大,该数值分析结果与结论1和2一致. 设a∈[0.1,0.9],b分别取0.2、0.4、0.6、0.8,其他参数取值如上文所述,研究此时SADBC的变化趋势,如图3所示. 图3 a和b对合作概率的影响Fig.3 The effect of a and b on cooperation probability 由图3可知,在成本分担系数b的4种不同取值下,SADBC关于a的函数图像均呈现“倒U型”,即其他参数取值一定时,随着a值不断增大,SADBC总是先增大至一个极大值后又逐渐减小.由此表明:当其他参数一定时,存在一个a值,使得SADBC取得极大值,即存在一个最优的超额收益分配比例,使二者合作的概率最大.该数值分析结果与结论3一致. 由图3可知,当a<0.5时,SADBC随着b的增大而减小,说明当快递企业的超额收益较少,承担的合作成本也相应越少时,双方合作的概率越大;当a>0.5时,SADBC随着b的增大而增大,说明当快递企业的超额收益较多,承担的合作成本也相应越多时,则双方合作的概率越大.总之,当快递企业与第三方智能快递柜企业对超额收益的分配比例与对合作成本的承担比例正相关时,双方合作的概率增大,该数值分析结果与结论4一致. 基于演化博弈理论对快递企业与第三方智能快递柜企业间的合作机制进行研究,得到如下结论:当超额收益大于合作成本时,二者才有开展合作的可能,且合作成本越小、超额收益越大,则越有利于二者合作;存在一个最佳的超额收益分配比例,使得二者合作的概率最大;超额收益的分配比例与合作成本的承担比例正相关时,合作概率增大. [1] 中华人民共和国国家统计局.中华人民共和国2016年国民经济和社会发展统计公报[N].经济日报,2017-03-01(005). [2] 杨永芳,王道平.民营快递企业的发展对策研究[J].预测,2011,30(2):71-76. [3] 刘明,杨路明.快递物流企业提升客户满意度研究[J].技术经济与管理研究,2015(9):72-75. [4] 杨静,张燕,陈涛.大数据时代快递企业竞争力研究-基于粗糙集理论[J].统计与决策,2015(13):179-181. [5] 刘立华.智能快递柜自助服务的应用及其发展方向[J].物流工程与管理,2015,37(8):54-55. [6] 杜荣雪,阮国祥.智能自提柜在城市社区应用的可行性分析[J].物流科技,2015(1):133-134. [7] 杜白.基于用户需求和进化博弈的认知无线电网络选择[J].郑州大学学报(工学版),2014,35(4):92-95. [8] 谢识予.经济博弈论(第三版)[M].上海:复旦大学出版社,2007:19-37. [9] SEIFERT R W, ZEQUEIRA R I, LIAO S. A three-echelon supply chain with price-only contracts and sub-supply chain coordination[J]. International journal of production economics, 2012, 138(2):345-353. [10] 张国兴,方帅,汪应洛.基于演化博弈的供应链协调机制分析[J].统计与决策,2015(15):45-49. [11] 黄敏镁.基于演化博弈的供应链协同产品开发合作机制研究[J].中国管理科学,2010,18(6):155-162. Abstract: The smart express cabinets could solve terminal distribution problems to some extent. Based on the view of evolutionary game theory, an evolutionary game model of express enterprises and third-party smart express cabinet enterprises was established in this paper. Meanwhile, the dynamic evolutionary process and factors influencing the establishment of cooperative relationship were analyzed by this model. Finally, numerical cases were conducted with Matlab simulation software. The results showed that: (a)Only the excess income was more than the cost, probably the cooperation could be achieved. (b)Probability of this cooperation had a positive correlation with the excess income, while inversely with the cost. (c)There existed an optimal proportion of excess income correlation, which could maximize the probability of cooperation. (d)Reasonable income distribution mechanism and cost sharing mechanism were conducive to the establishment of the cooperative relationship. Keywords: terminal logistics;cooperation mechanism;evolutionary game;smart express cabinets;express enterprises EvolutionaryGameAnalysisonCooperationMechanismofExpressEnterprisesandThird-partySmartExpressCabinetEnterprises LI Yumin, YANG Lu, WANG Xinlu (School of Management Engineering, Zhengzhou University, Zhengzhou 450001, China) 李玉民(1969— ),男,河南南阳人,郑州大学教授,博士,主要从事物流与供应链管理研究,E-mail:li.yu.min@163.com. TP23;F272.3 A 10.13705/j.issn.1671-6833.2017.05.009 2017-03-11; 2017-06-19 国家自然科学基金资助项目(71501173);河南省科技攻关计划项目(122102310399、132102310310) 1671-6833(2017)05-0081-051.2 模型构建



2 演化稳定策略分析
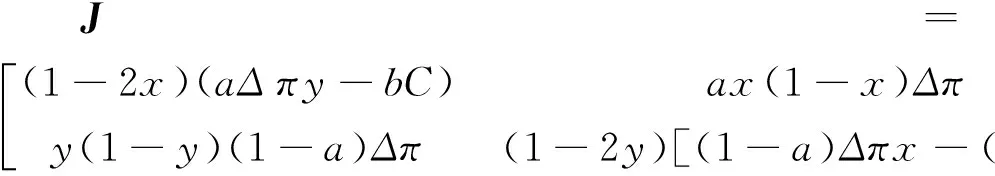
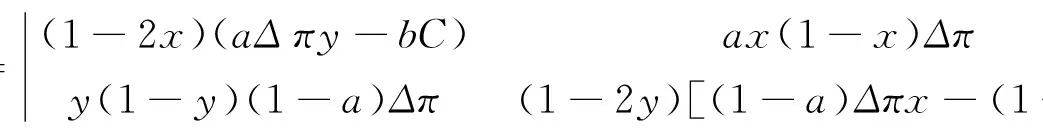
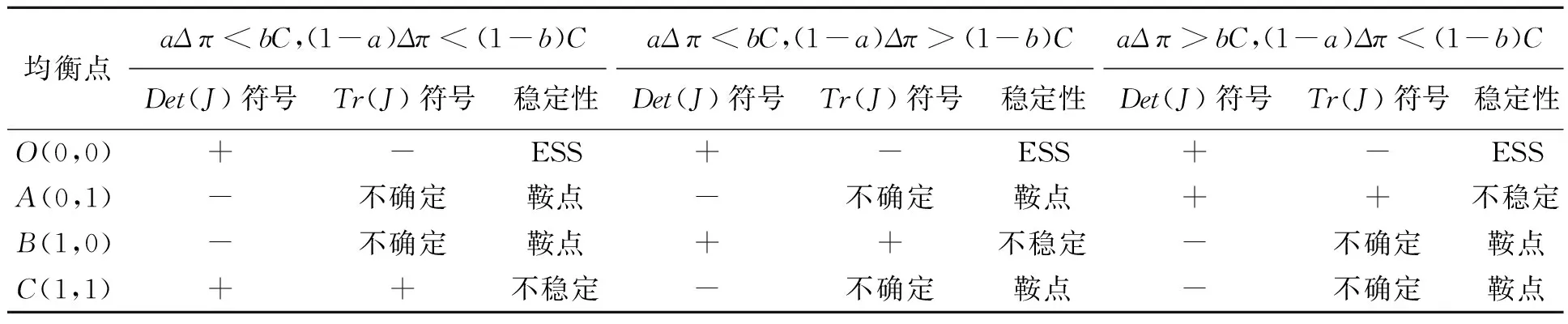
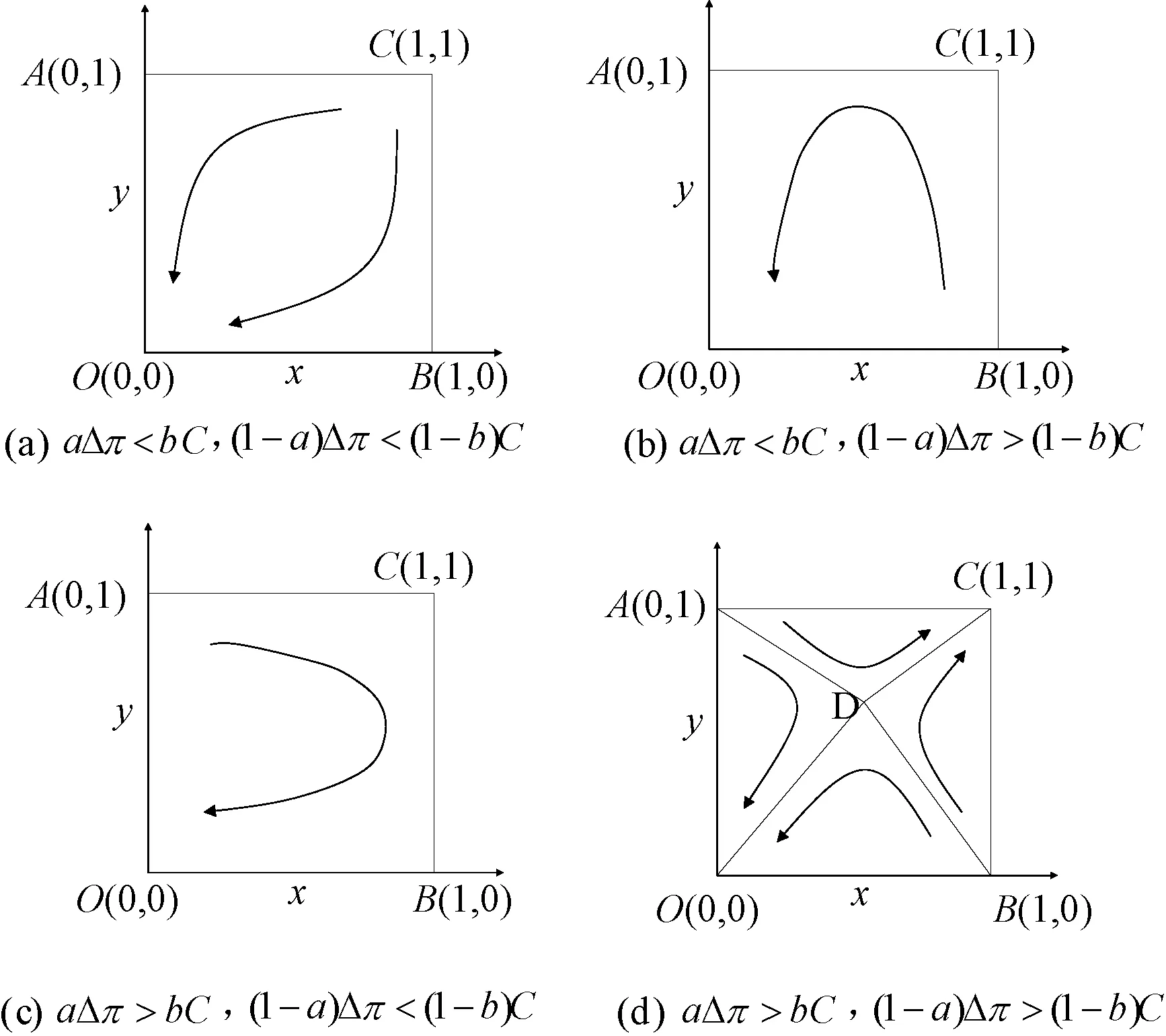
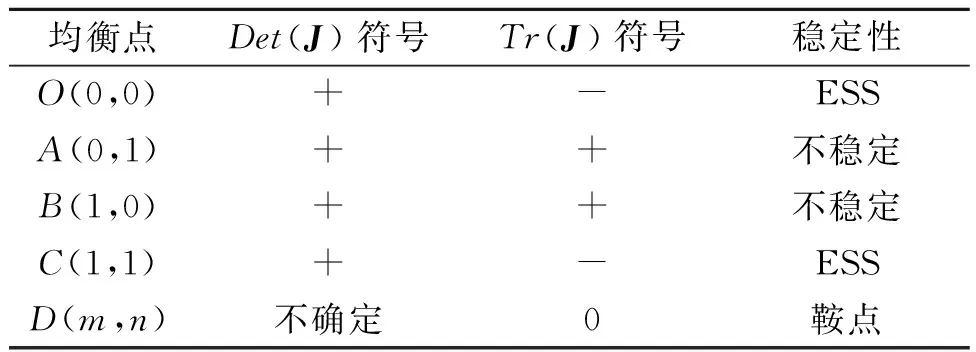
3 二者合作的影响因素分析

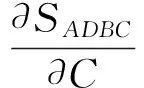
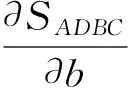
4 算例分析
4.1 合作成本及超额收益对合作的影响
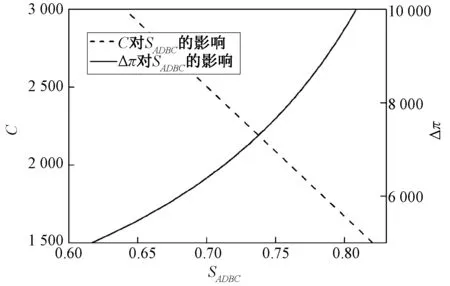
4.2 超额收益分配比例及成本分担比例对合作的影响

5 结论
