基于粒子群算法的烧结炉系统辨识及神经网络控制

曹 奔， 袁忠于， 刘 洪

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

基于粒子群算法的烧结炉系统辨识及神经网络控制

曹 奔， 袁忠于， 刘 洪

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

烧结炉在加热过程中，模型参数易发生变化，而传统的PID控制很难达到理想的控制效果.本文运用粒子群优化算法辨识烧结炉的数学模型，针对烧结炉惯性大、时变、大滞后等特点，采用基于RBF神经网络的监督控制，将PID控制与神将网络控制相结合.当温度或模型参数发生较大变化时，PID控制起主要作用，神经网络起调节作用，补偿PID控制的不足.MATLAB软件仿真结果说明，该方法能够提高烧结炉的控制精度，具有一定的实用性.

粒子群算法；系统辨识；神经网络监督控制；PID控制

0 引言

聚四氟乙烯(PTFE)被称为“塑料王”，具有耐酸、耐碱、自润滑性、易加工成型等优异性能，广泛用于制作机械密封圈等部件[1].各种PTFE预成型品经烧结才能成为优良的制品，烧结过程就是将预成型品加热至晶体熔点327 ℃以上，并在此温度下保持一段时间，使聚合物分子由结晶形转变为无定形[2].炉温调节是烧结过程中的重要环节，制品的性能很大程度上取决于温度控制的精度.

研究系统的动态特性实质是要建立对象的数学模型，用数学方法表示各参数之间的关系[3].系统建模方法有机理建模和实验建模两种，机理建模是根据基本的物理定律建立相应的数学模型.实验建模分为阶跃响应法、频率法、相关分析法、最小二乘法等.阶跃响应法试验方法简单，应用较广，但不是所有的系统都允许加入阶跃扰动，而且对扰动幅值也有限制；频率法计算复杂，精度较低；相关分析法需要求解卷积方程，计算比较困难；最小二乘法已广泛运用到系统辨识，但是估计的模型结构是差分方程型式，不利于系统分析和计算[4].文献[5]采用粒子群算法和最小二乘法混合优化算法对模糊模型参数进行辨识；文献[6]采用粒子群算法实现对系统的结构和参数识别.笔者采用粒子群优化算法辨识系统参数模型，可以灵活地选择合适的模型结构，然后利用算法估计出模型参数，把系统辨识问题转化为参数优化问题[4].

烧结炉在升温、保温和降温等阶段要求不同，系统模型参数也随之发生变化.纯滞后，时间与温度之间存在非线性关系，需要对烧结过程采用分段控制[7-8].文献[9]采用模糊自适应PID控制烧结炉温度，但是没有建立模糊规则；文献[10]采用两个神经网络分别调节PI控制器参数，与传统PI控制器相比，缩短了加热炉响应时间.笔者针对烧结炉惯性大、时变、大滞后等特点，采用基于RBF神经网络与PID相结合的方法，当对象参数发生变化或出现较大误差时，PID控制起主导作用，神经网络起监督调节作用，使系统快速趋于稳定[11].仿真结果显示，笔者提出的方法能够提高烧结炉的控制性能.

1 烧结炉模型分析

烧结炉具有大惯性和大滞后性，根据其特征，可以总结出烧结炉的经验模型[7]：

(1)

烧结炉装置又是一个具有自平衡能力的对象，根据烧结炉系统的特征，也可以用等容多阶对象或多容惯性对象作为粒子群算法辨识的模型结构.

等容多阶对象[4]：

(2)

(3)

式中：Kp为比例系数；Tp为惯性时间常数；τ为纯迟延时间常数；n为惯性部分的阶次;s为进化代数.

2 粒子群优化算法系统模型辨识

2.1 粒子群算法原理

粒子群算法(particle swarm optimization,PSO)是由Kennedy和Eberhart在1955年模拟鸟类捕食行为提出的群体智能算法.该算法采用全局搜索策略，计算速度快，适用于求解非线性、多参数复杂系统的全局优化问题[5].假设一个D维的空间由n个粒子组成，粒子在种群中的位置Xi=(xi1,xi2,…xiD)Τ, 第i个粒子的速度为Vi=(Vi1,Vi2,…,ViD)Τ,将Xi带入目标函数即可计算出每个粒子位置所对应的适应度值.其个体极值Pi=(Pi1,Pi2,…,PiD)Τ，种群的群体极值Pg=(Pg1,Pg2,…,PgD)Τ，在每次迭代过程中，粒子根据式(4)更新自己的速度，根据式(5)更新自己的位置.

(4)

Xid(k+1)=Xid(k)+Vid(k+1)，

(5)

式中：ω为惯性权重；d=1,2,…,D；i=1,2,…,n；k为当前迭代次数；Vid为粒子的速度；c1和c1为加速度因子；r1和r2是分布于[0,1]区间的随机数.

2.2 粒子群算法系统辨识原理

系统辨识包括对函数结构和系统参数的辨识，其实质就是函数拟合的过程[4].笔者将粒子群优化算法用于烧结炉系统参数辨识，根据系统的实际输入输出数据x(t)和y(t)，估计出系统模型f与真实模型在一定精度上相似，即

y(t)=f[X(t,ε)]，

(6)

式中：t=kT，T为采样周期，k=1,2,3，…，N;ε为估计模型的参数.

在实际系统中，往往存在测量误差、外界干扰、系统自身误差等，估计模型不可能完全替代真实模型，因此，需要在估计模型中加入残差e(t).实际系统估计模型为：

y(t)=f[X(t,ε)]+e(t).

(7)

假定模型结构为经验模型(1)，则需要优化的未知参数为：Kp、Tp、τ、n，粒子在种群中的位置向量Xi、速度向量Vi、个体极值向量Pi和种群极值向量Pg的结构为[Kp,Tp,τ,n]，运用粒子群优化算法原理，将系统模型辨识转化为未知参数优化求解的问题.模型(1)的差分方程为[4]：

x1(k+1)=e-d/Tpx1(k)+KP(1-e-d/Tp)u(k)；

(8)

x2(k+1)=e-d/Tpx2(k)+(1-e-d/Tp)x1(k+1)；

(9)

xn(k+1)=e-d/Tpxn(k)+(1-e-d/Tp)xn-1(k+1)；

(10)

f(k+1)=xn(k+1-τ/d)，

(11)

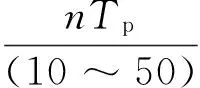
由式(7)可知，残差e(t)绝对值越小，估计模型越逼近实际的系统模型.选择合适的误差指标函数更新粒子的位置和速度，求取残差绝对值最小时的估计模型参数.定义误差指标函数

(12)

3 系统辨识与仿真

3.1 粒子群算法系统辨识步骤

根据模型参数辨识的原理，结合粒子群算法实现烧结炉系统辨识.

①采集烧结炉系统的输入、输出信号并画出图像，如果采集信号存在粗大值，采用低阶差分法加以剔除.

②选择恰当的估计模型结构，确定估计模型参数，文中加速因子c1、c2取0.6,粒子个数m=50，进化代数s=80，然后定义各参数区间.

③编辑目标函数子程序，计算估计模型输出f和误差指标函数值，运用粒子群算法进行调用并优化模型参数.

④参数优化按照粒子群优化算法的步骤进行，如图1所示.

图1 粒子群算法流程图Fig.1 Flow chart of particle swarm algorithm

3.2 实例仿真

选取文献[12]的烧结炉加热系统数学模型作为烧结炉的真实模型，即

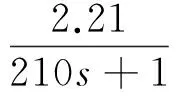
(13)

在阶跃信号激励下生成辨识所用的历史数据，加入实际测量时的随机扰动，然后选择烧结炉经验模型结构，Kp∈(0.1,10),Tp∈(1,300),τ∈(1,100),n∈(1,5).将辨识结果的阶跃响应与真实模型比较,辨识结果如表1所示,仿真结果如图2所示.

表1 PSO算法辨识结果和真实值阶跃响应

图2 经验模型辨识结果与实际模型响应输出Fig.2 Empirical model identification results and the actual model response output

带有纯延迟的模型不利于系统分析，在选择估计模型结构时，可选用高阶惯性模型描述，即：Kp∈(0.1,10),Tp∈(1,300)，n∈(1,5).高阶惯性模型对采集的原始数据具有滤波作用，使得辨识结果更加准确.将辨识结果的阶跃响应与真实模型比较，仿真结果如图3所示.采用高阶对象辨识结果为：

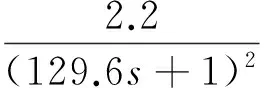
(14)

图3 高阶惯性模型辨识结果与实际模型响应输出Fig.3 High order inertia model identification result and actual model response output

为了描述烧结炉具有自平衡的细节，选择多容惯性对象作为系统估计模型结构，Kp∈(0.1,10),Tp1～pn∈(1,500),n∈(2,5).将辨识结果的阶跃响应与真实模型比较，仿真结果如图4所示.采用多容惯性对象辨识结果为：

(15)

图4 多容惯性模型辨识结果与实际模型响应输出Fig.4 Multi-capacity inertia model identification result and actual model response output

4 基于RBF神经网络的监督控制

神经网络控制具有自学习和自适应的能力，能够适应烧结炉时变的特点，提高控制器的鲁棒性.RBF神经网络的监督控制就是初始阶段采用PID控制，然后再用神经网络控制.如果在控制过程中，产生干扰或出现较大误差，在PID控制的同时，神经网络控制通过修正参数起到调节的作用[11].其原理如图5所示.

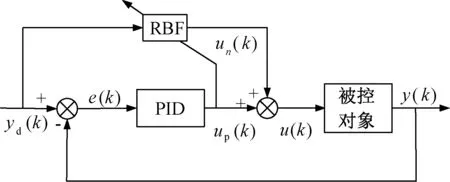
图5 基于RBF神经网络的监督控制系统Fig.5 Supervisory control system based on RBF neural network

在RBF神经网络结构中，设h=[h1,…,hm]Τ，hi为高斯函数，

(16)

总控制输入为：

u(k)=un(k)+up(k).

(17)

定义误差指标为：

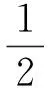
(18)

式中：x(k)为网络的输入向量；cj为网络第j个结点的中心矢量，cj值离输入越近，高斯函数对输入越敏感；bj为结点j的宽度参数，高斯基函数宽度是影响网络映射范围的重要因素；up(k)为PID控制器的输出；un(k)为RBF神经网络的输出.

权值ω采用梯度下降法更新，加入学习速率η和动量因子α，

Δωi(k)=η(un(k)-u(k))hj(k).

(19)

ω(k)=ω(k-1)+Δω(k)+α(ω(k-1)-

ω(k-2)).

(20)

为了检验RBF神经网络监督控制系统的响应速度和跟踪效果，仿真对象选取带延迟的一阶对象，其传递函数如下：

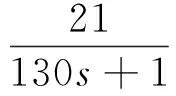
(21)

PID控制器中，Kp=8，Ki=0.002，Kd=0.4.参考轨迹选取方波信号yd(k)=0.5×sign(sin(pi×k×t)).根据经验，高斯函数参数初值c=[-2, -1, 1, 2]，b=[1, 1, 1, 1]，权值ω取随机数，学习速率η=0.3，动量因子α=0.05.仿真结果如图6所示.由图6可见，基于RBF的神经网络监督控制系统跟踪效果良好.

图6 RBF神经网络监督控制系统跟踪响应结果Fig.6 RBF neural network monitoring control system tracking response

烧结炉在实际加热过程中，不同温区滞后时间不同；而且每次添加烧结材料的种类和数量不同，相当于模型参数发生变化[13].为了模拟现场实际情况，测试模型参数变化时系统的控制效果，假定初始时刻，仿真对象为文献[13]中利用切线法确定的低压真空烧结炉温度控制系统传递函数：

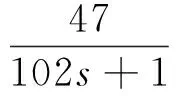
(22)

在350 min时变换对象的模型，即

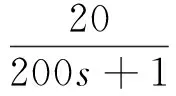
(23)

[14]聚四氟乙烯烧结成型的制备工艺，升温速度：200 ℃以下为80 ℃/h，高于200 ℃为60 ℃/h；烧结温度为380 ℃；保温4 h后制品随炉温冷却[14].PID控制器中，kp=1.4，ki=0.01，kd=0.05.根据经验,高斯函数参数初值c=[-400, -400, 400, 400]，权值ω取随机数，b=[7, 7, 7, 7]，学习速率η=0.3，α=0.05，图7为炉温控制仿真.如图7所示，350 min时模型参数发生变化，控制系统过渡时间较短，仿真结果说明了该方法的有效性.

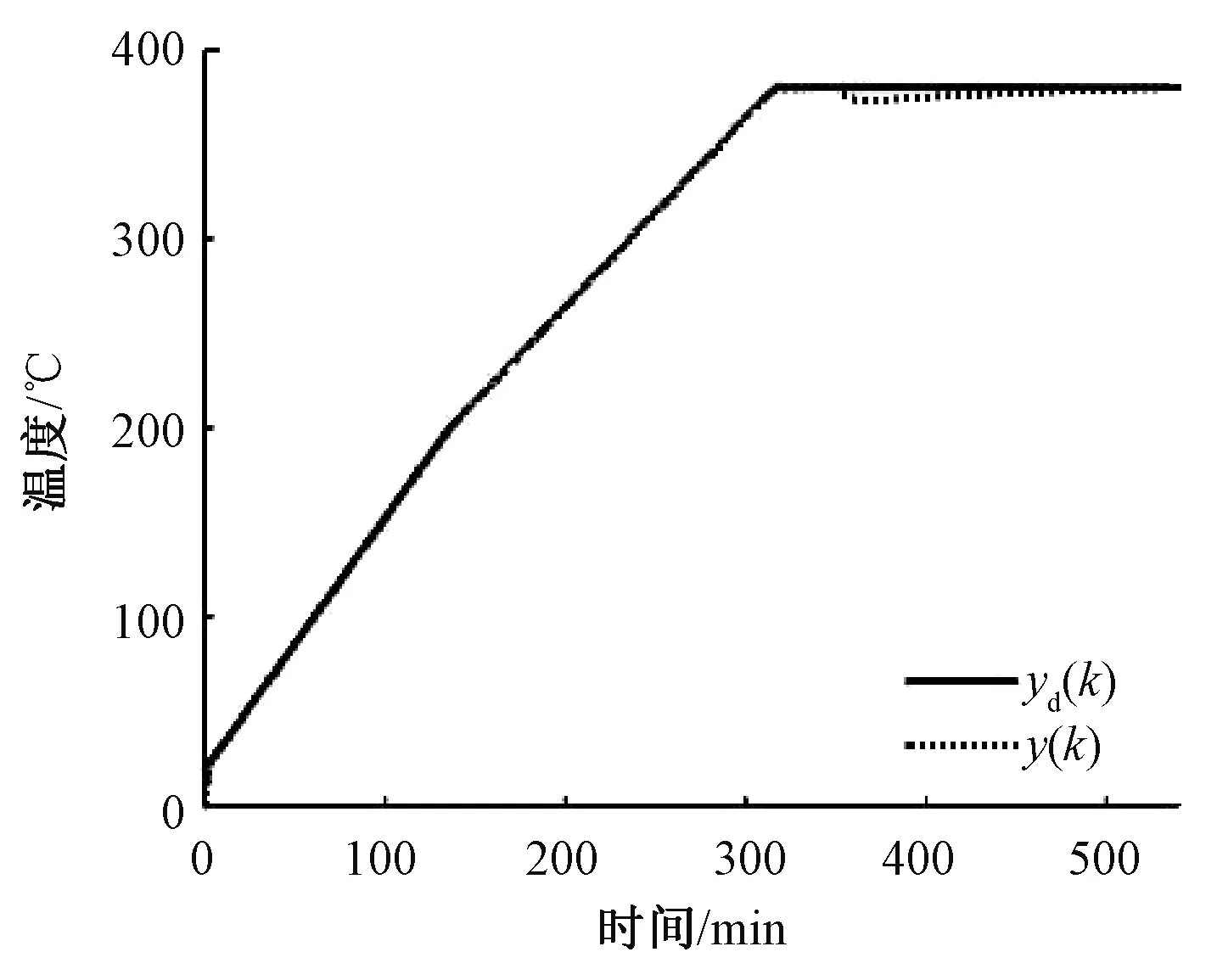
图7 烧结炉炉温控制仿真结果Fig.7 The simulation result of sintering furnace temperature control

5 结论

采用粒子群优化算法对烧结炉系统进行模型辨识，选择不同的模型结构作为估计模型，将辨识结果的阶跃响应与真实模型作比较，说明粒子群辨识系统模型方法的有效性.针对烧结炉的特点，控制系统采用基于RBF神经网络监督控制方法.仿真实验表明，系统响应速度较快，跟踪效果良好；当烧结炉参数发生变化时，系统能够通过参数调节，快速达到设定温度.

参考文献：

[1] 龚成龙. 聚四氟乙烯烧结炉计算机控制系统[J]. 电气自动化,2007,29(1):51-53.

[2] 王进华. 关于模压用聚四氟乙烯树脂烧结工艺条件的探讨[J]. 有机氟工业,2000(3):21-23.

[3] 王骥程.过程控制工程[M].北京:化学工业出版社,1990.

[4] 韩璞.智能控制理论及应用[M].北京：中国电力出版社,2012.

[5] 刘雪，张端金.基于Delta算子时滞网络控制系统的Hoo滤波[J]. 郑州大学学报(工学版),2016,37(2):10-14.

[6] DENG X. System identification based on particle swarm optimization algorithm[C]// International conference on computational intelligence and security, IEEE, 2009:259-263.

[7] 凌云,何丽平,李毅梅. 硬质合金真空烧结炉温度插值自适应控制[J]. 硬质合金,2007,24(2):112-114.

[8] 凌云,何丽平,李毅梅.基于DRNN在线辨识的真空炉温度控制[J]. 微计算机信息,2007,23(4):110-111.

[9] BABULU K, KUMAR D K. Fuzzyself-adaptiveself-adaptive PID controller design for electric heating furnace[J]. International journal of engineering inventions, 2012, 1(5): 10-21.

[10] EREMENKO Y I, POLESHCHENKO D A, GLUSHCHENKO A I. On applying neural tuner to PI-controller parameters calculation for heating furnaces control[C]//Control and Communications (SIBCON), 2015 International Siberian Conference on IEEE, 2015: 1-4.

[11] 刘金琨.RBF神经网络自适应控制MATLAB仿真[M].北京：清华大学出版社,2014.

[12] 刘京朋. 基于仿人智能控制的烧结炉监控系统的实现[D].成都：电子科技大学自动化工程学院,2009.

[13] 张施磊. 低压真空烧结炉自动控制系统研究与设计[D].重庆：重庆大学自动化学院,2006.

[14] 陈旭,回素彩. 聚四氟乙烯烧结成型的制备工艺[J]. 塑料工业,2005,33(10):38-40.

Abstract: During heating process of sintering furnace, the model parameters were easy to change, and traditional PID control was difficult to achieve the desired control effect. This paper used particle swarm optimization algorithm to identify the mathematical model of sintering furnace, for sintering furnace with high inertia, time-variation and strong time delay etc, a method of supervision and control based on RBF neural network, which combined PID control with neural network control. When temperature or parameters changed greatly, PID control played a major role. neural network played a regulatory role and compensated the shortage of PID control. The simulation results of MATLAB software showed that this method could improve the control precision of sintering furnace, which had a certain practicality.

Keywords: particle swarm optimization algorithm; system identification; neural network supervisory control; PID control

SinteringFurnaceSystemIdentificationBasedonParticleSwarmAlgorithmandNeuralNetworkControl

CAO Ben, YUAN Zhongyu, LIU Hong

(School of Mechatronic Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

TP273

A

10.13705/j.issn.1671-6833.2017.02.022

2016-09-30；

2016-11-19

国家自然科学基金资助项目(51565025)

袁忠于(1968— )，男，甘肃兰州人，兰州交通大学副教授，主要从事复杂系统建模及智能控制研究.

1671-6833(2017)05-0039-05