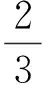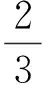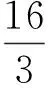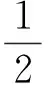断裂或接触力学问题中第二类柯西奇异积分方程的一种解析方法
2017-10-10金晓清吕鼎张向宁李璞周青华胡玉梅
金晓清,吕鼎,张向宁,李璞,周青华,胡玉梅
(1.重庆大学 机械传动国家重点实验室, 重庆400044; 2.四川大学 空天科学与工程学院, 四川 成都610065)
断裂或接触力学问题中第二类柯西奇异积分方程的一种解析方法
金晓清1,吕鼎1,张向宁1,李璞1,周青华2,胡玉梅1
(1.重庆大学 机械传动国家重点实验室, 重庆400044; 2.四川大学 空天科学与工程学院, 四川 成都610065)
第二类柯西奇异积分方程因涉及复奇异因子往往造成求解困难,而适用第一类奇异积分方程的高效数值方法并不能推广至第二类奇异积分方程,即便是第二类奇异积分方程,其数值解法仍是一个难题. 为此提出了构造第二类奇异积分方程解析解的一种新方法. 通过分解柯西奇异项,并利用雅克比多项式的正交性,推导针对右端载荷项为单项式(monomial)的递推解析解,进而借助级数展开的方法推广至一般的载荷问题. 提出的基于递推的解析解构造方案,能完美地结合maple软件编程,从而提供一种方便、快捷、有效的算法. 由给出的算例可见,本方法适用于处理界面断裂或接触分析问题中含复数奇异因子的复杂情形,从而为研究该类典型力学问题提供了一种可供选择的方法.
第二类奇异积分方程;柯西主值积分;复数奇异因子;界面裂纹
0 引 言
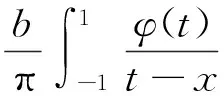
(1)
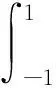
(2)
其中L为已知给定量.
在已有文献中,第一类奇异积分方程求解方法相对成熟[7-10],第二类柯西奇异积分方程求解较难,要获取其封闭解析解尤为困难[11]. 现有研究大多局限于奇异积分方程的数值解法,典型成果有:ERDOGAN等[7]和KRENK[8]采用的正交多项式法和GERASOULIS等[12]采用的分段多项式方法. MILLER等[13]采用分段二阶多项式,以数值求解第二类奇异积分方程. JIN等[14-15]讨论了上述各方法的利弊,并提出一种针对第二类奇异积分方程的有效数值解法. 周薇等[6]和周跃亭等[16]对第二类奇异积分方程的配置法、内插型求积公式法和机械求积法等数值解法进行了论述.
对于第一类奇异积分方程,正交多项式法[7-10]求解效率高,并且易于编程. 然而,此方法很难推广到第二类奇异积分方程[7],其所探讨的求解方案[4]计算复杂、编程困难且效率不高.分段多项式法(piecewise polynomial approach)[12-13, 17-20]允许积分点和配置点(collocation point)任意分布,但当近似多项式的阶次相对较小时,解的收敛速度和精度[18, 21]难以达到最优.虽然通过提高近似多项式的阶次理论上可使函数解更精确,但其积分式将变得繁复难解[13, 17, 20]. 由此可见,第二类柯西奇异积分方程的数值解法较为烦琐,至今仍缺少一种针对性强且高效的方法. 笔者借助maple软件,通过分解柯西奇异项,利用雅克比多项式的正交性,提出一种实用的求解第二类奇异积分方程的解析新方法.
1 解析解计算方法
根据Muskhelishvili指数理论(index theory)[2],式(1)中φ(x)可以表示成新待求函数g(x)和反映问题物理奇异性态的基函数(fundamental function)ω(x)的乘积:
φ(x)=g(x)ω(x),
(3)
其中g(x)满足Hölder连续条件,而
ω(x)=(1-x)α(1+x)β,
(4)
将式(3)(4)代入式(1),式(1)左端含柯西核的第2项可改写为
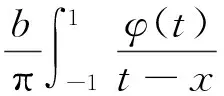
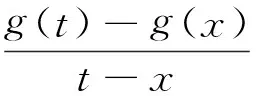
(5)
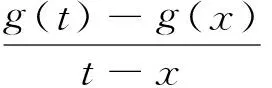
(1-x)α(1+x)βcot(απ)+I(x),
(6)
其中,
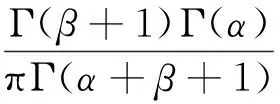
(7)
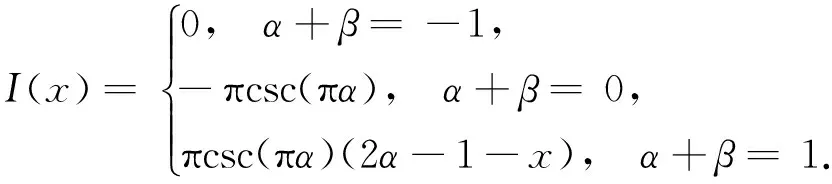
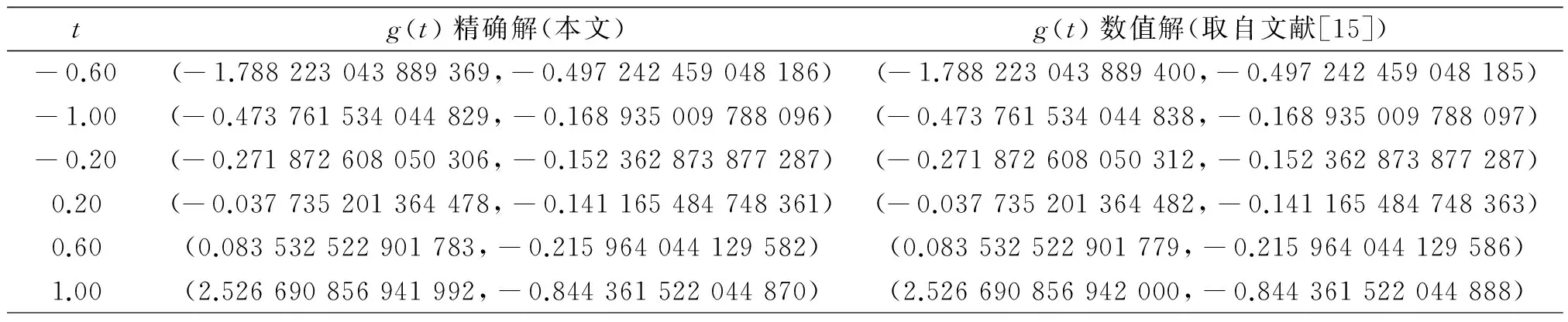
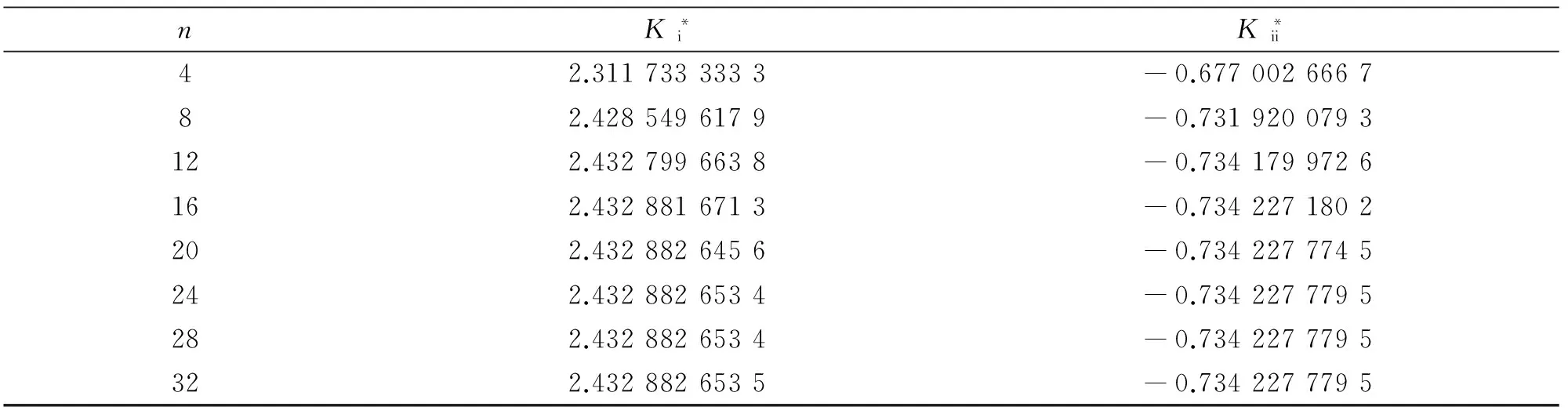
(8)
在界面裂纹问题中,两端裂尖具有物理奇异是一种典型的情况,此时α和β的实部取值满足-1 当I(x)消失时,式(1)可化为 |a+bcot(απ)|ω(x)g(x)+ (9) 通过适当选取α值,式(9)中的第1项可化为0,即求: a+bcot(απ)=0, (10) 当系数a和b为复数时,α和β的值可由下式确定: (11) 其中整数N的取值需考虑问题于区间左端点-1处的物理奇异特性,即满足-1 (12) 下面先讨论载荷为单项式(monomial)即f(x)=xn的情况. 由式(3)(4)(11)可知,求解式(1)中的φ(x)只需求解式(12)中的g(x).联立式(4)~(12),此时式(1)变换为如下形式: (13) 因载荷为n阶高次项,可设g(t)为n+1阶多项式:g(t)=c0+c1t+c2t2+c3t3+…+cn+1tn+1, (14) 故求解φ(x)即为求解g(t)中待定系数cn(n=0,1,2…)的值. 将多项式(14)代入,式(13)中积分项关键部分可变换为 (15) 其中di(t)表示式(15)中xi项的系数,即 di(t)=ci+1+ci+2t+…+cn+1tn-i. (16) (17) (18) 雅克比多项式与权函数(1-t)α(1+t)β相关,存在如下正交特性: (19) 特别地,0阶雅克比多项式等于1.由式(19)可知,非0阶雅克比多项式存在如下性质: (20) (21) 将式(15)~(17)代入式(13),利用式(21),积分方程(13)可转化为如下代数关系: (22) (23.0) (23.1) (23.i) (23.n) (24) 式(23)对应的关系转变为 (25.0) (25.1) … (25.i) … (25.n) g(t)=c0+c1t+c2t2+c3t3+c4t4. (26) (27) 即 φ(x)=ω(x)g(x)=-sinαπ(1-x)α(1+x)β× (28) 式(1)~(12)给出了一种求解第二类奇异积分方程的新方法.上述变换主要有2个目的: 回顾文献[24]中界面裂纹的例子,其控制奇异积分方程为 (29) 满足 (30) 式(29)中实常数γ与两各向同性弹性介质材料性质有关,等式右边的f(x)与裂纹面上的法向和切向载荷的综合作用有关.指数α和β的值由式(11)确定: (31) 在此情况下,利用附录A中给出的maple程序,得到边界未知函数的封闭解: g(x)=-sin(πα)[3x5+(6α+4)x4+ (6α2+8α+1)x3+4α(α+1)2x2+c1x+c0], (32) 其中, (33) 表1为利用本方法求得的精确解与文献[15]给出的数值计算结果的比较,两者符合良好,在计算机的舍入误差范围内,验证了本文给出的载荷f(x)为单项式xn的解析解. 且利用单项式载荷解析解构造多项式载荷解析解的方法可行.相应的maple程序见附录. 第(ii)种载荷条件是泰勒级数展成多项式的组合. 将右端指数项进行泰勒展开,得到x的多项式,利用本方法近似求解. 随着泰勒级数的增加,计算结果会逐渐收敛于精确解. 利用maple软件并逐次增加多项式项数,得到裂纹右尖端的复应力强度因子的计算值如表2所示,有效数收敛至小数点后10位. 从数值结果中可看出,收敛速度令人满意. 通过分解柯西奇异项,消除奇异积分方程中的柯西奇异性,以便解析求解第二类奇异积分方程. 本解析方法可以用来处理界面裂纹中的物理奇异性问题,结合maple软件编程,方便易行,对复数奇异因子同样适用.从而,为获取第二类柯西奇异积分方程的封闭解析解提供了一种切实可行的新途径. 表1 本文精确解与文献[15]数值解对比 表2 载荷(ii)情况下,例2中右裂尖应力强度因子(SIF)的数值收敛解 [1]GAKHOVFD.BoundaryValueProblems[M]. New York: Dover,1990. [2] MUSKHELISHVILI N I. Singular integral equations: Boundary problems of function theory and their application to mathematical physics[J].PNoordhoffN,2008,24(2):256-291. [3] HILLS D A, KELLY P A, DAI D N, et al. Solution of crack problems: The distributed dislocation technique[J].JournalofAppliedMechanics,1998,65(2):548. [4] 张耀明,孙翠莲,谷岩.边界积分方程中近奇异积分计算的一种变量替换法[J].力学学报,2008,40(2):207-214. ZHANG Y M, SUN C L, GU Y. The evaluation of nearly singular integrals in the boundary integral equations with variable transformation[J].ChineseJournalofTheoreticalandAppliedMechanics,2008,40(2):207-214. [5] 刘俊俏,段惠琴,李星.SH 波在压电材料条中垂直界面裂纹处的散射[J].固体力学学报,2010,31(4),385-391. LIU J Q, DUAN H Q, LI X. The scattering of sh wave on a vertical crack in a coated piezoelectric strip[J] .ChineseJournalofSolidMechanics,2010,31(4),385-391. [6] 周薇.在接触力学中的奇异积分方程的高精度数值解法[D].成都:电子科技大学,2011. ZHOU W.High-AccuracyNumericalSolutionforSingularIntegrationEquationsinContactMechanics[D]. Chengdu:University of Electronic Science and Technology of China,2011. [7] ERDOGAN F, GUPTA G D, COOK T.NumericalSolutionofSingularIntegralEquations[M].Berlin / Netherlands: Springer,1973,1(6):368-425. [8] KRENK S. On quadrature formulas for singular integral equations of the first and the second kind[J].QuarterlyofAppliedMathematics,1975,33(3): 225-232. [9] THEOCARIS P, IOAKIMIDIS N. Numerical integration methods for the solution of singular integral equations(for crack tip stress intensity factor evaluation in elastic media)[J].QuarterlyofAppliedMathematics,1977,35(1): 173-183. [10] ERDOGAN F, GUPTA G. On the numerical solution of singular integral equations[J].QuarterlyofAppliedMathematics,1972,29(4): 525-534. [11] 李星.积分方程[M].北京:科学出版社,2008. LI X.IntegralEquation[M]. Beijing: Science Press,2008. [12] GERASOULIS A, SRIVASTAV R. A method for the numerical solution of singular integral equations with a principal value integral[J].InternationalJournalofEngineeringScience,1981,19(9): 1293-1298. [13] MILLER G R, KEER L M. A numerical technique for the solution of singular integral equations of the second kind[J].QuarterlyofAppliedMathematics,1985,42(4): 455-465. [14] JIN X.AnalysisofSomeTwoDimensionalProblemsContainingCracksandHoles[D]. Chengdu: Northwestern University,2006. [15] JIN X, KEER L M, WANG Q. A practical method for singular integral equations of the second kind[J].EngineeringFractureMechanics,2008,75(5): 1005-1014. [16] 周跃亭,李星.具周期裂纹的半平面周期接触问题的奇异积分方程数值解法[J].固体力学学报,2005,26(2): 167-174. ZHOU Y T, LI X. Singular integral equation method for periodic contact problem of an elastic half-plane with periodic cracks[J].ChineseJournalofSolidMechanics,2005,26(2): 167-174. [17] KIM P, LEE S. A piecewise linear quadrature of Cauchy singular integrals[J].JournalofComputationalandAppliedMathematics,1998,95(1/2): 101-115. [18] GERASOULIS A. Piecewise-polynomial quadratures for Cauchy singular integrals[J].SiamJournalonNumericalAnalysis,1986,23(4): 891-902. [19] GERASOULIS A. The use of piecewise quadratic polynomials for the solution of singular integral equations of Cauchy type[J].Computers&MathematicswithApplications,1982,8(1): 15-22. [20] KURTZ R D, FARRIS T N, SUN C. The numerical solution of Cauchy singular integral equations with application to fracture[J].InternationalJournalofFracture,1994,66(2): 139-154. [21] RABINOWITZ P. Convergence results for piecewise linear quadratures for Cauchy principal value integrals[J].MathematicsofComputation,1988,51(184): 741-747. [22] IOAKIMIDIS N I. On the numerical evaluation of derivatives of Cauchy principal value integrals[J].Computing,1981,27(1): 81-88. [23] ERDELYI A, MAGNUS W, OBERHETTINGER F, et al .TablesofIntegralTransforms:VolII[M]. New York / Toronto / London: McGraw-Hill,1954. [24] THEOCARIS P S, IOAKIMIDIS N I. On the numerical solution of Cauchy type singular integral equations and the determination of stress intensity factors in case of complex singularities[J].ZeitschriftFürAngewandteMathematikundPhysik,1977,28(6):1085-1098. 以本文的界面裂纹为例,说明maple程序的编制及调用. 当载荷为n-1阶单项式时,可利用SIEslover子程序得到g′π(x)的解析式,其中g′π(x)=g(x)/cn. 将多项式载荷视为多个单项式的叠加,根据力学叠加原理,利用本程序可求解载荷条件(i)的情况. 同时,本程序也能求解载荷条件(ii)下α为复数的情况. >SIEslover:= proc (n,x, alpha) localpx,rx,i,j,Pj,cPj,cRj,c; c[n]:= 1; px:=c[n]; foritondo px:=px*x; rx:=px; forjfromiby -1 to 1 do Pj:= normal(simplify( JacobiP(j, alpha, -1-alpha,x), 'JacobiP')); cPj:= coeff(Pj,x^j); cRj:= coeff(rx,x^j); rx:= normal(simplify(rx-cRj*Pj/cPj)) od: c[n-i]:= -rx; px:=px+c[n-i] od: px:= collect(px, [x], factor) end: 下面为本求解器的调用示例: 载荷条件(i) >f5:= SIEslover(5,x, alpha); f4:=SIEslover (4,x, alpha); f1:=SIEslover (1,x, alpha); f1:=2α+x+1; 载荷条件(ii) >alpha:= -1/2-1/10*′I; >res2:= SIEslover (1,x, alpha); >forito 35 do c[i]:=coeff(taylor(2*exp(x*x),x= 0, 40),x^i); res2:=simplify(res2+c[i]* SIEslover (i+1,x, alpha)); sif:=evalf(subs(x= 1, res2), 20); k1:=Re(sif); k2:=Im(sif); if modp(i,5)=0 then printf("i=%3d,…k1 +Ik2 =%+15.10f,+I%+15.10f
",i,k1,k2) end if od: JIN Xiaoqing1, LYU Ding1, ZHANG Xiangning1, LI Pu1, ZHOU Qinghua2, HU Yumei1 (1.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;2.School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, China) Due to the presence of complex singularity, solutions to the singular integration equation (SIE) of the second kind are still under development. As a matter of fact, numerical methods for SIE of the first kind are hardly applicable to SIE of the second kind. With the assistance of maple programming, this paper presents a novel approach to formulate an analytical solution to a typical SIE of the second kind. By splitting the Cauchy kernel, and taking advantage of the orthogonality of Jacobi polynomials, we derive an analytical solution corresponding to the monomial loading case. Furthermore, the solution to a general loading case may be obtained via series expansion. The present method appears efficient and convenient, providing an effective tool for treating tangentially loaded contact analyses and interface crack problems. SIE of the second kind;Cauchy principal value integration;complex singularity; interface crack 10.3785/j.issn.1008-9497.2017.05.009 O 343.3; O 346.1 :A :1008-9497(2017)05-548-07 2016-04-13. 国家自然科学基金资助项目 (51475057);中央高校基本科研业务费专项(106112017CDJQJ328839). 金晓清(1974-),ORCID:http://orcid.org/0000-0002-8836-3505,博士,研究员,博士生导师,主要从事断裂疲劳、细观力学、摩擦学等研究,E-mail:jinxq@cqu.edu.cn. AnanalyticalmethodforsolvingCauchysingularintegralequationsofthesecondkindwithapplicationstofractureandcontactanalyses.Journal of Zhejiang University (Science Edition), 2017, 44(5 ): 548-554
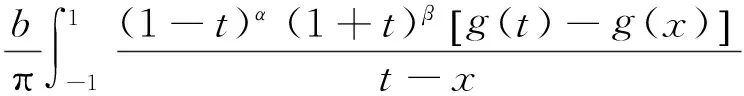
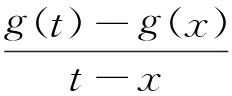
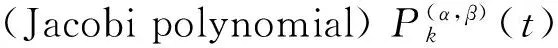
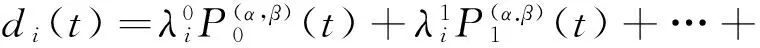
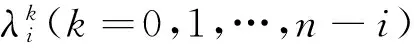
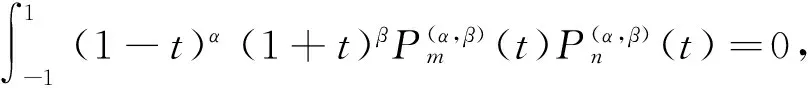
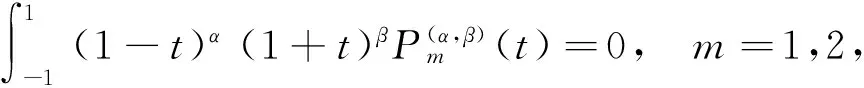
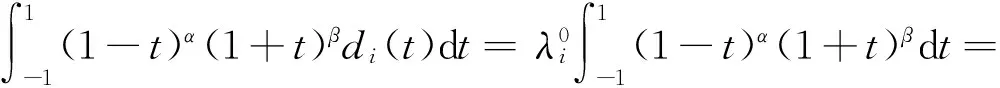
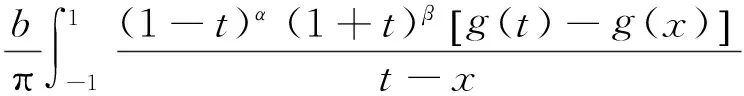
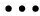
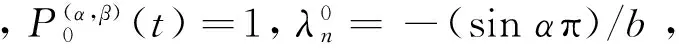
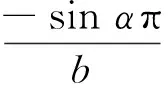
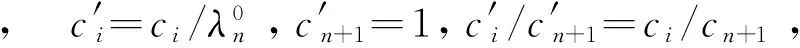
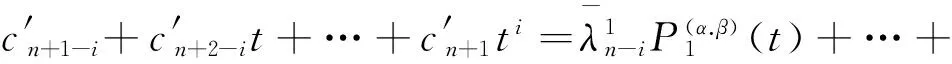
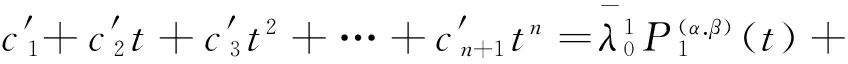
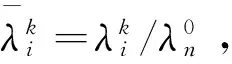
2 算例讨论
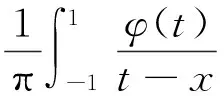
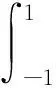
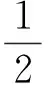
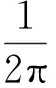
3 结束语
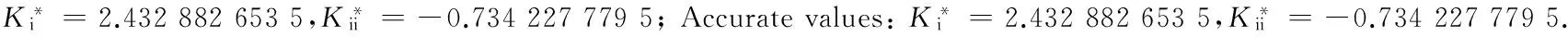
附录:maple程序