热工过程数据驱动子空间预测控制的研究

景亚杰， 朱小良

(东南大学 能源与环境学院， 南京 210096)

热工过程数据驱动子空间预测控制的研究

景亚杰， 朱小良

(东南大学 能源与环境学院， 南京 210096)

为改进目前火电机组机炉协调系统预测控制的效果，在多模型子空间预测控制研究的基础上，利用子空间方法直接从数据中得到预测控制器，并将数据驱动子空间预测控制与基于子空间的多模型预测控制两种控制策略进行仿真比较，结果表明所研究的控制方法可行且有效，为进一步研究提供了思路。

机炉协调系统； 数据驱动模型； 子空间辨识； 多模型； 预测控制

Abstract： To improve the predictive control effect of current boiler-turbine coordinated system in coal-fired power unit, on the basis of predictive control research for multi-model subspace, the subspace method was used to obtain data directly from predictive controller. Simulation results of both the data-driven subspace predictive control and subspace-based multi-model predictive control were compared. Results show that the method proposed is feasible and effective, which may serve as a reference for further research of similar problems.

Keywords： boiler-turbine coordinated system; data-driven modeling and control; subspace identification; multi-model; predictive control

对于热力发电厂而言，控制系统的控制效果好坏影响着整个电厂的经济性和安全性。在热力发电厂的机炉协调系统中，由于存在多变量、时变、变量间强耦合、非线性和时延迟等特点，导致控制任务实现的过程中存在很多障碍。同时，大型电厂为了满足电网负荷调节的需求，经常需要改变功率输出。电厂频繁地大范围变负荷运行，使得非线性对控制效果的影响进一步加剧。因此，热力发电厂控制系统需要更先进可靠的控制方案来尽可能减少这种非线性影响，以提高机炉协调控制系统的控制性能和提高电厂效率。为此，各种控制策略，如智能PID[1]、模型预测控制[2]、H∞控制[3]、增益调度控制[4]等，已被研究并应用。一般控制策略中，要设计一个控制器，首先需要构建一个模型。由于状态空间模型可以反映系统的内部行为及系统输入和输出的关系[5]，很多学者以状态空间模型的形式设计多变量预测控制系统。得到状态空间模型的方法很多，比如采用泰勒级数展开的线性化方法转化为状态空间矩阵，但该方法会增加设计控制器的复杂性。

文献[6]中提出一种使用输入输出数据，进行子空间辨识来获得状态空间模型的控制方法。该方法借助QR分解、奇异值分解等数学工具，辨识过程不涉及迭代，文献[7]最后的仿真也验证了其有效性，但目前这种控制策略在热力发电厂这类非线性系统的研究中还不够深入。杨华[8]提出通过子空间辨识直接得到控制器的思路，而笔者研究的数据驱动子空间预测控制的方法正是按照这种思路利用子空间辨识直接从数据中得到控制器。因为模型是直接从数据中得到的，那么数据中的信息一定不少于模型，所以直接从数据中建立控制器理论上完全可以实现。数据驱动子空间预测控制不需要辨识状态方程，而是由子空间预估矩阵直接设计预测控制器，与转化为状态空间模型的控制方法相比，省去了求解状态方程再得到控制器的过程，减少了计算的复杂性。笔者最后通过局部工况区间的仿真验证了这一控制策略的可行性，由于仿真只验证了局部工况区间，如何在大范围的工况区间取得好的控制效果需要进一步研究。

1 系统描述

根据热力发电厂机炉协调系统的低阶非线性结构，可以选取某160 MW燃油机组作为研究对象。该机组在国内外预测控制领域的研究中已被多次作为研究对象，非常具有代表性，经验公式可靠，约束条件简单。吴啸[7]提出的基于子空间的多模型预测控制策略仿真时也选择了该模型，选择160 MW燃油机组也便于仿真时两种策略分析比较。

热力发电厂主要受到给煤量、一次风量、引风量、给水量等多个控制变量的影响；被控变量主要有炉膛压力、主蒸汽压力、汽包水位、输出功率、烟气含氧量等，且各个被控变量之间还存在不同程度的耦合情况。机组协调系统的任务是保证输出功率快速地跟随负荷的变化，同时压力、温度和水位等波动需在允许的范围内。所以笔者选取了3个最重要的输入变量和3个最重要的输出变量作为研究对象。3个控制输入变量分别为：燃料阀门开度u1、主汽阀门开度u2和给水阀门开度u3。3个被控输出变量分别为：汽包压力p、输出功率E和汽包水位偏移L。3个中间状态变量分别为汽包压力p、输出功率E和汽水密度ρ。160 MW燃油机组的动态方程如下[9]：

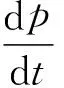
(1)

(2)

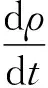
(3)

该机组的约束条件是：

该约束条件的物理意义是控制阀门变动大小和调节速率的限制。

汽包水位可以通过下式求解得到：

L=50(0.13ρ+60α+0.11q-65.5)

(4)

其中，

q=(0.85u2-0.14)p+45.59u1-2.51u3-2.09α=(1/ρ-0.001 5)/(1/(0.8p-25.6)-0.001 5)

式中：α为蒸汽质量，kg；q为蒸发率，kg/s。

研究的机炉协调系统的7个典型工况点见表1[7]，给定负荷指令时可在工况点处选择。表1中：x1、x2、x3分别表示汽包压力p、输出功率E和汽水密度ρ；u1、u2、u3分别表示燃料阀门开度、主汽阀门开度和给水阀门开度；y3表示汽包水位偏移L。

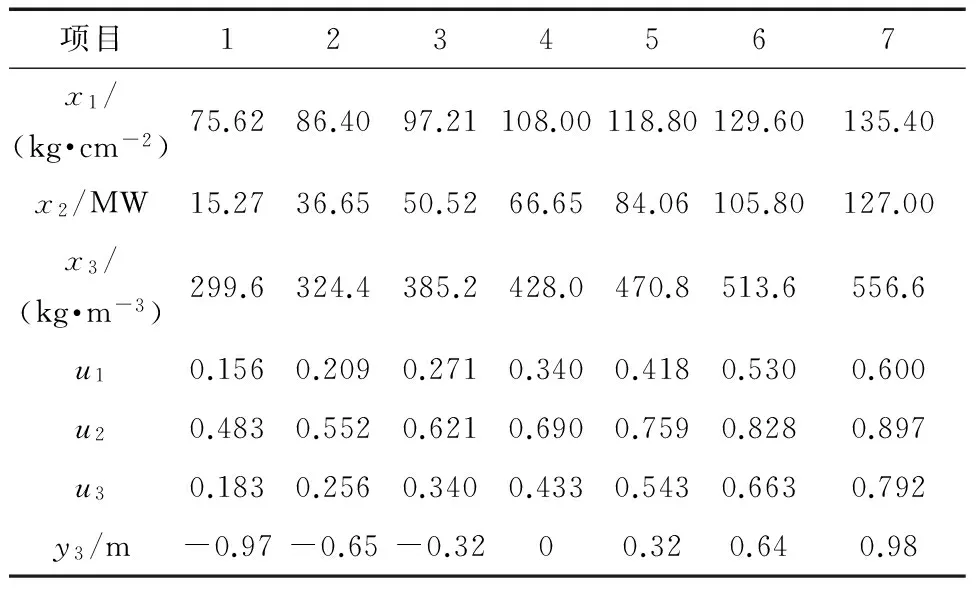
表1 机炉协调系统模型典型工况点

2 子空间预测控制

2.1 基于子空间模型的多模型预测控制

局部线性模型是通过子空间辨识得到状态空间模型确定，然后通过组合局部线性模型逼近原始系统的非线性模型，该方法已在文献[7]中详细讲解。

2.2 数据驱动子空间预测控制

对于热力发电厂这样的多变量输入、多变量输出控制系统而言，其过程受到多种因素的影响，通常选取最主要的控制量和被控量构建预测控制器。在得到已知数据后，分别把输入变量和输出变量的n次测量数据按如下矩阵形式给出[8]：

[u0,u1,…,un]

(5)

[y0,y1,…,yn]

(6)

其中每个元素可表示为：

a、b分别表示选取的输入变量和输出变量的个数，均取3。

然后由已知测量数据分别构造过去输入、未来输入、过去输出和未来输出的Hankel矩阵UP、UF、YP和YF，形式如下：

(7)

(8)

(9)

(10)

ui和yi分别是由输入输出数据组成的列向量。

定义矩阵：

(11)

然后按下式左边的组合矩阵进行QR分解:

(12)

根据下式得到子空间矩阵[8]：

(13)

式中：+表示矩阵的伪逆；SW称作状态子空间矩阵；SU称作确定性的输入子空间矩阵[10]。

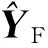
(14)

其中，

从上述步骤中可以看出子空间预测控制器的获取过程并没有用到非线性迭代，因此适合在线使用。结合常规的预测控制的思想，定义性能指标J为：

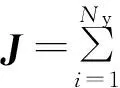
(15)

该式包括跟踪性能指标和调节性能指标。其中：rk+i为k时刻参考输出；Q和R分别为加权矩阵，可以人为定义或调整；Ny、Nu分别为预测时域和控制时域，它们的大小会影响控制器的快速性和稳定性。如果预测时域越小，那么跟踪性能越差，所以必须有一定的预测步数来保证跟踪效果；反之预测时域越大的话，计算量会增加很多，系统的稳定性和鲁棒性会受影响。同样控制时域也跟稳定性和快速性有关系。控制时域越小，跟踪的效果不会太好；控制时域越大，系统的稳定性会受影响。根据之前研究学者的经验，可以选择预测时域和控制时域的步数为10步左右。

根据式(14)和(15)对目标函数进行改写：

J= -SuufQfrf-rfQfSuuf+SuufQfSwWp+

(16)

式中：rf为参考输出，即期望的输出值；Qf、Rf为加权矩阵。

(1) 用最新的输入输出数据更新Hankel矩阵Up、Uf、Yp、Yf。

(2) 用特征值求解的方法在线求解。

(3) 按照公式获得子空间矩阵Sw、Su。

(4) 对目标函数或性能指标进行二次规划，得到最优控制序列uf。

(5) 取优化控制序列的第一个分量加到被控系统中去，在下一个时刻，转到步骤(1)，如此依次循环即可实现完全数据驱动的子空间预测控制。

数据驱动子空间预测控制方法基本的原理如上所述，具体应用时还要注意噪声干扰等常见问题。

2.3 两种方法的比较

基于数据驱动的子空间预测控制方法的优势如下：(1)该方法与多模型预测控制相比，不需要知道或构造机组的非线性模型，只需要知道机组的输入输出数据，由于其数据驱动的特性，该预测控制策略可以用于机组非线性模型未知的情况；(2)直接采用数据驱动，不需要构建局部状态空间模型，避免了模型失配的弊端，具体计算过程相比多模型等预测控制简洁。

基于子空间模型的多模型预测控制方法之所以繁琐，是因为其还需要采用标准开环子空间[8]等方法来辨识局部模型矩阵和卡尔曼滤波增益K，并把所有的局部模型变换到统一的基上。考虑到卡尔曼滤波器的稳定性，需满足N→∞，其中N是输出数据Hankel矩阵的行块数。该方法建立的Hankel矩阵用QR分解和奇异值分解时需满足以下条件： (1)输入变量与噪声不相关；(2)以2N阶次持续激励输入变量；(3)采样数目足够大。基于子空间方法的多模型预测控制基本原理见图1。

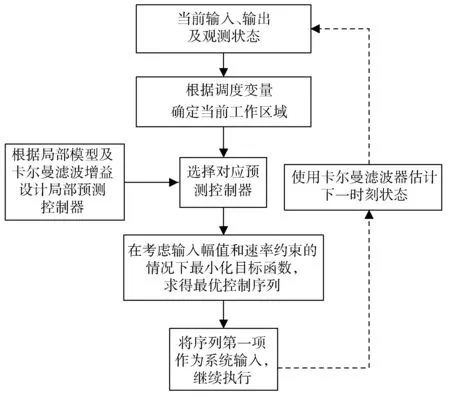
图1 基本原理

从图1可以看出：每进入下一时刻状态，局部模型矩阵和卡尔曼滤波增益K都需要重新计算，而直接数据驱动的子空间预测控制方法则不需要计算状态空间模型矩阵及卡尔曼滤波增益设计，自然矩阵计算量也相应减少。

3 仿真验证

3.1 初始输入输出变量数据

笔者选用工况点5的数据118.8 kg/cm2、84.06 MW、0 m分别作为汽包压力p、输出功率E、汽包水位L的初值，而燃料阀门开度、主汽阀门开度和给水阀门开度初值分别为0.418、0.759、0.543。汽水密度的数值是470.8。利用数学工具充分激励机组的经验模型获得足够的输入变量和输出变量的数据(见图2)。

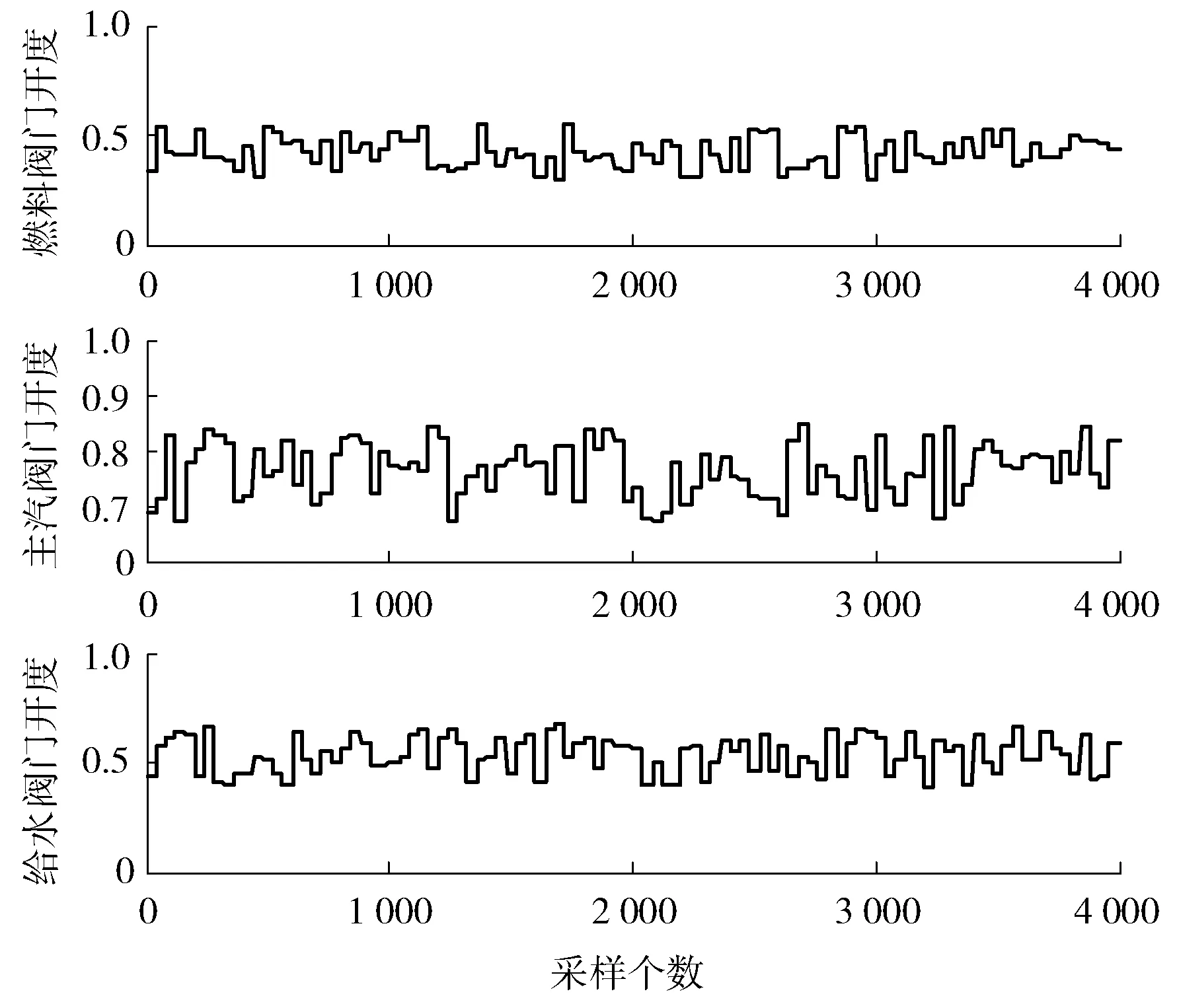
图2 辨识所用输入信号

将输入变量的数据利用三个机组模型动态方程依次计算出输出变量数据(见图3)。

图3 机炉协调系统的输出数据

3.2 CCS指令模式下的仿真

CCS指令模式下电厂控制任务是跟踪汽包压力和控制输出功率在预期工作点，同时保证汽包水位正常。为快速响应负荷，CCS同时向锅炉和汽轮机发出指令，协调两者控制系统的工作状态。该指令多为阶跃变化，使系统可以尽可能地发挥机组的调频和调峰能力，稳定机组运行参数。

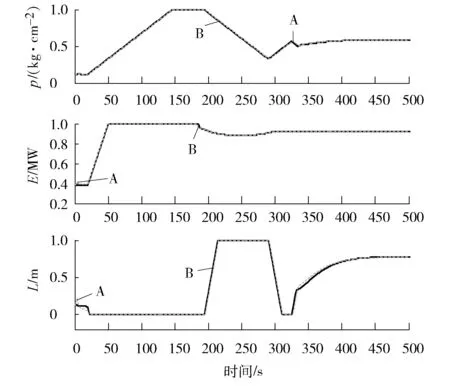
笔者同时进行了两种仿真，分别为数据驱动子空间预测控制和基于子空间模型的多模型预测控制，其仿真结果见图4和图5。

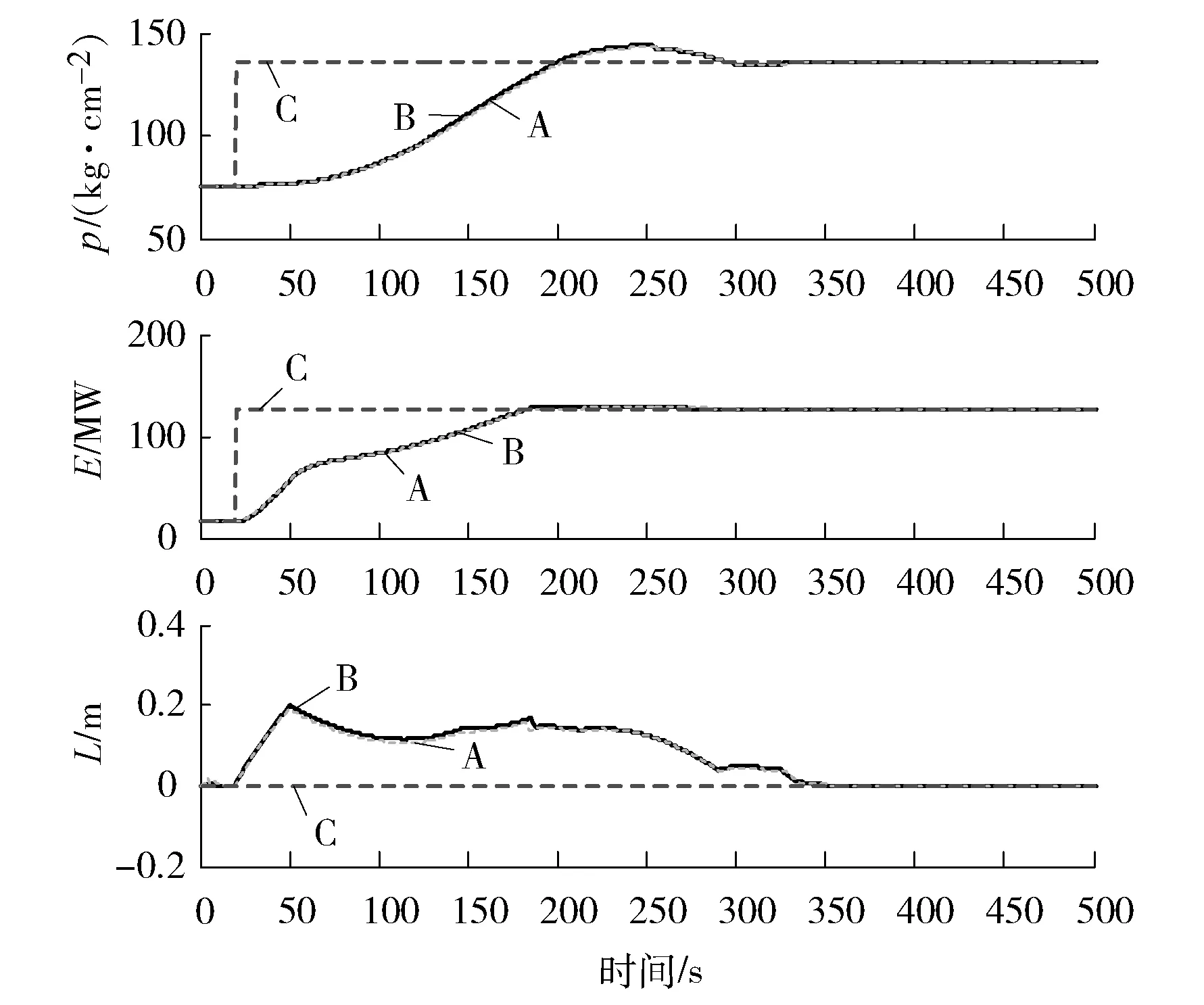
A—数据驱动子空间预测控制；B—基于子空间模型的多模型预测控制；C—参考值。

图4 在CCS方式下锅炉机组的输出变量性能

A—数据驱动子空间预测控制；B—基于子空间模型的多模型预测控制。

图5 在CCS方式下锅炉机组的输入变量性能

图4反映出两种控制方法的仿真性能很接近。虽然两种控制方法有着非常接近的控制效果，然而多模型预测控制需要预先知道系统的非线性模型，再通过整合多个局部近似线性模型，从而设计控制器，故该方法的应用受到限制。此外，基于子空间模型的多模型预测控制，需要额外计算局部状态空间模型及卡尔曼滤波器增益设计，还需要把多个局部线性模型转化到共同的基下，从而得到整体的多模型控制系统，这些都使得该方法比直接数据驱动的方法计算的数据多，而本身机组控制系统计算数据量就很大。而数据驱动的子空间预测控制只需要知道输入输出数据就可以实现预测控制，避免了模型失配的影响，可以被简单灵活地应用于不同对象，在不清楚机组模型的情况下可以尝试采用，以便机组控制系统进行研究或应用。

从输入变量的仿真曲线看出：3个输入变量主汽调节阀最先动作，可以迅速调节机组输出功率；给水阀门开度变化最大，这是因为汽包水位跟汽水密度、蒸发率和汽包压力等多个扰动相关，所以汽包水位的控制需要频繁地调节给水阀门开度。但3个控制变量的波动时间不算太长并最终趋于稳定，符合热工过程控制系统的变化规律。

然而该仿真只是表明所选择的局部工况点附近两种预测控制方法吻合较好，当因负荷指令变化或因煤种、天气、加热器性能变化等引起的变工况，即数据与设计控制器时所选择的工况不匹配的情况下，采用局部数据驱动子空间预测控制方法的效果将会打折扣。

4 结语

针对热力发电厂机炉协调系统进行了数据驱动子空间预测控制的方法研究和局部工况区间的仿真验证，并与基于子空间的多模型预测控制策略进行了比较。仿真结果证明了数据驱动子空间预测控制的可行性和有效性，即只考虑最重要的控制变量和被控变量而不考虑其他扰动时，数据驱动的子空间预测控制可以跟随负荷指令变化，平稳地达到期望值，且阀门调节开度被约束在指定范围内。值得关注的是，数据驱动所提出的建模和控制方法非常灵活，可以容易地适应其他类型的系统，而不需要精确地知道机组具体的数学模型，这也是它最大的优点。如果要实现数据驱动子空间预测控制在机炉协调系统全局工况内的应用，还需要进一步研究补充控制器在不同工况区间的过渡控制方法，以使控制器的控制性能达到最优。

[1] DIMEO R, LEE K Y. Boiler-turbine control system design using a genetic algorithm[J]. IEEE Transactions on Energy Conversion, 1995, 10(4): 752-759.

[2] WU X, SHEN J, LI Y G, et al. Stable model predictive control based on TS fuzzy model with application to boiler-turbine coordinated System[C]//Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). Orlando, FL: IEEE, 2011: 2981-2987.

[3] WU J, NGUANG S K, SHEN J, et al. Robust H∞ infinite tracking control of boiler-turbine systems[J]. ISA Transactions, 2010, 49(3): 369-375.

[4] CHEN P C, SHAMMA J S. Gain-scheduled -optimal control for boiler-turbine dynamics with actuator saturation[J]. Journal of Process Control, 2004, 14(3): 263-277.

[5] FENG G. A survey on analysis and design of model-based fuzzy control systems[J]. IEEE Transactions on Fuzzy Systems, 2006, 14(5): 676-697.

[6] VAN OVERSCHEE P, DE MOOR B. A unifying theorem for three subspace system identification algorithms[J]. Automatica, 1995, 31(12): 1853-1864.

[7] 吴啸. 协调控制系统的子空间辨识及预测控制[D]. 南京: 东南大学, 2014.

[8] 杨华. 基于子空间方法的系统辨识及预测控制设计[D]. 上海: 上海交通大学, 2007.

[9] MAYNE D Q, RAWLINGS J B, RAO C V, et al. Constrained model predictive control: stability and optimality[J]. Automatica, 2000, 36(6): 789-814.

[10] WU X, SHEN J, LI Y G, et al. Data-driven modeling and predictive control for boiler-turbine unit[J]. IEEE Transactions on Energy Conversion, 2013, 28(3): 470-481.

StudyonSubspacePredictiveControlDrivenbyThermalEngineeringProcessData

Jing Yajie, Zhu Xiaoliang

(School of Energy and Environment, Southeast University, Nanjing 210096, China)

2016-10-13；

2017-01-10

国家自然科学基金项目(51076027)

景亚杰(1993—)，男，在读硕士研究生，研究方向为热工过程测量与自动化控制。

E-mail: 2582664065@qq.com

TK321

A

1671-086X(2017)05-0315-06