基于改进ORB特征检测的多视角图像拼接

李 文，李小艳

(仰恩大学)

基于改进ORB特征检测的多视角图像拼接

李 文，李小艳

(仰恩大学)

针对多视角图像拼接方法中存在的实时性较差，以及拍摄图像是存在运动物体产生的拼接裂缝和“GHOST”现象，提出基于改进ORB特征检测的多视角图像拼接.通过对ORB算法的改进使得图像的特征点提取和匹配有更高的实时性和稳定性，且通过采用较低复杂度的动态规划算法找到最佳缝合线，最后对拼接后的图像通过泊松融合进行平滑处理，从而对多视角图像中存在的拼接裂缝和“GHOST”现象有很好的抑制作用.

ORB算法；多视角拼接；动态规划算法；泊松融合

0 引言

多视角图像通过拼接可以展现更加生动和丰富的信息，且图像拼接的技术的好坏将直接影响用户的体验感.图像配准和图像融合是图像拼接的两个关键技术，目前现有的特征点提取和匹配算法中SIFT[1](Scale Invariant Feature Transform)、SURF[2](Speeded Up Robust Features)、ORB(Oriented FAST and Rotated BRIEF)等算法随着精度依次递减而速度在增加[3]，在对拼接后的图像进行处理时，若通过梯度差和色彩强度差构建缝合线准则式，运用Dijkstra算法寻找缝合线并对图像的曝光差异进行补偿，并在融合时使用多分辨率样条算法[4]，但Dijkstra算法相对复杂且多分辨率样条会使合成后的图像噪声较大.

为解决上述问题，提出基于改进ORB特征检测的多视角图像拼接，提高了特征点提取和匹配的速度且特征点分布均匀，从而满足了多视角图像拼接的实时性和稳定性，在寻找最佳缝合线时使用复杂度相对较低的动态规划算法，最后采用泊松融合算法对拼接后的图像进行平滑处理.

1 ORB算法

2011年Rublee等人在ICCV上提出了ORB[5]算法，该算法对ORB算子加入了FAST[6](Features from Accelerated Segment Test)特征的方向信息的同时，使用FAST算法对特征点进行检测，在特征点描述时利用BRIEF[7](Binary Robust Independent Elementary Features)算法，ORB算法还改进了BRIEF不具备旋转不变性和对图像噪声敏感的缺点.ORB特征提取可以分为两部分：(1)具有方向的FAST算子检测；(2)具有旋转不变性的BRIEF算子描述.

1.1算子检测

使用分割检测判据进行FAST特征点检测，在以像素点p为中心，如果半径为r的圆周上存在联系的n个像素Ik(其中k=1,2,…,n)，通过下式可判断像素点p是否为角点：

其中Ik为任意一个像素点的灰度值；像素点p的灰度值为Ip，t是已知的一个很小的阈值，若CRF=1的个数多于一个给定的阈值t′，将该点视为候选点，通常t′=12.如图1所示.

图1 FAST特征点检测

通过建立图像金字塔引入尺度特性，并通过灰度质心法[8]去除顶特征点的方向，使FAST兴趣点具有方向并依据此方向来提取BRIEF算子.

1.2生成具有旋转不变的算子

ORB算法的算子使用对BRIEF算子添加了旋转不变性的rBRIEF.BRIEF算法首先在提取的特征点附近随机选取若干点对组成图像块，然后将这些图像块二值化处理后形成一个二进制串作为该特征点的特征算子.将随机选取的两个二进制点做比较得到BRIEF算子的一位.定义经过高斯核平滑处理的图像块p的二进制比较准则τ为：

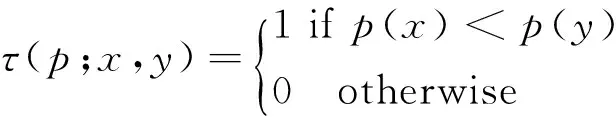
其中，图像块p在像素点x=(u,v)和y处的灰度值分别为p(x)和p(y)，选择n个(x,y)像素位置对，就可以得到BRIEF的n为二进制比特串：

其中，n可以为128，256，512等.

BRIEF算子主要通过对图像的微分符号进行编码，即BRIEF算子进行二进制编码是通过比较图像中相应位置的强度大小.因此，该算子对光照具有较好的鲁棒性，但是对旋转和噪声较敏感，为解决ORB算法对噪声的敏感问题，利用高斯滤波器(Gaussian Filter)对图像进行预处理，从BRIEF算子的运算速度和鲁棒性的角度出发，将高斯核方差取值为2.离散核窗口尺寸使用由每个小块(5×5像素)构成的图像块对(31×31像素)，通过对比小块图像的像素值之和，同时ORB算法给出两种方法来解决BRIEF算子不具有旋转不变的缺点：

(1) 通过控制FAST特征点的方向使得BRIEF算子对旋转变化保持不变性，对于任意特征点序列来说，在(xi,yi)像素位置的n个二进制为准则，定义一个2×n的矩阵S：

使用关键点及周围邻域构成的5×5像素图像小块的方向θ和对应的旋转矩阵，建立Sθ∶Sθ=RθS.此时受控制的BRIEF算子变为

gn(p,θ)=fn(p)|(xi,yi)∈Sθ.

(2) 通过使用贪婪穷举算法找到相关性较低的随机点对使得BRIEF算子对旋转变化保持不变性，即通过贪婪穷举的搜索方法找到相关系数接近0.5的图像点对.

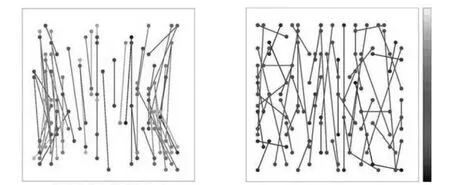
(a)较高相关性的随机点对(b)较低相关性的随机点对图2 贪婪穷举算法寻找随机点对

如图2所示，图2(a)表示为BRIEF特征引入主方向后，随着特征点主方向的不断变换使得随机点对的相关性变大，图2(b)为采用贪婪穷举算法后使得特征点相关性降低的结果，其右边的彩条为特征点在每次测试中的相关性，颜色越浅相关性越高，黑色相关性最低.

Michael等人[9]提供了5种在S×S像素大小的图像块上产生n个(xi,yi)位置对的采样方案，而ORB算法选择使用xi，yi都呈Gauss分布(0,1/25s2)的采样准则，该准则具有不同方向性能一致的同一Gauss分布的特点.

2 基于改进ORB算法的多视角图像拼接

2.1 ORB算法的改进

由于ORB算法特征点的提取和匹配精度相比SIFT、SURF等算法较低，且FAST检测出的特征点不含有尺度不变信息，导致ORB算法不具备尺度不变性，使得即使引进FAST特征点的方向使其具有旋转不变性，但其仍不具有尺度不变性.而SIFT算法使用多尺度空间理论提取稳定特征点，以及后续的特征点描述及匹配，使得该算法具有较好的尺度不变性，而这正是解决ORB算法不具有尺度不变性所需要的.同时在特征点提取期间，对特征分布和特征点数目进行改进.使用SIFT算法求出特征点和其质心方向后，用ORB算子描述特征点，最后生成具有旋转不变性和尺度不变性的算子并进行匹配，并在该过程中对特征点数目和特征分布进行改进，这样既使原始ORB算法具备尺度不变性，又保留了其旋转不变性和计算速度快速的特点.具体步骤如下：(1)借鉴SIFT算法的思想，建立尺度空间并求出极值点；(2)为解决ORB算法不具备尺度不变性的缺点，去除主曲率大于8和对比度较低的极值点；(3)在求出特征点质心方向后求取ORB算子；(4)在特征点提取期间对特征点数目和特征分布进行改进.

(1)极值点检测

Lindeberg等人已经证明[10]，某些受限制的条件下，Gauss函数是唯一尺度空间的核平滑函数.将图像F(x,y)的尺度定义为函数

L(x,y,σ)，其中σ为尺度因子，其由图像F(x,y)与Gauss函数G(x,y,σ)卷积后得到

L(x,y,σ)=G(x,y,σ)F(x,y)

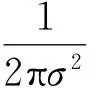
为了在尺度空间中得到稳定的特征点，在图像卷积得到的空间D(x,y,σ)与Gauss差分函数中寻找极值点，将其局部极值点视为尺度空间的候选特征点.

D(x,y,σ)=[G(x,y,kσ)-

G(x,y,σ)]F(x,y)=L(x,y,kσ)-L(x,y,σ)

上式中，常数k分开相邻的两个尺度.

(2)稳定的特征点的提取

在完成极值点的检测后，需去除一些不稳定的极值点，使得在进行特征点匹配时精确度和稳定性更好，使用3维的2次函数求在某个尺度上求得的极值点在原图像上的位置，并且将低对比度的极值点去除掉.首先在某极值点处对

D(x,y,σ)进行泰勒展开有：

(1)

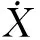
(2)

将式(2)带入式(1)中有：

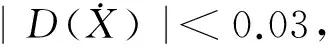
设H最大、最小特征值分别为α和β，则有

上式可知极值点D的主曲率与H的特征值对应成比例，则只需关心α/β的值，设γ=α/β且可知

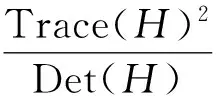
上式的结果与具体特征值无关与其值之间的比例有关，其中随着γ的增加(r+1)2/r也增加.则通过下式来检查主曲率的比值是否小于某一阈值γ:

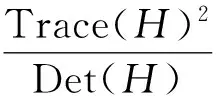
杜京义等人指出阈值γ=8[11]，即认为主曲率比值不大于8的极值点保留，其他极值点被去除.

2.2最佳缝合线的寻找

在特征点提取和匹配之后，可知两帧图像间的交叠区域并搜索最佳缝合线，若进行拼接可能会因为光线和移动等原因使得图像模糊，造成“GHOST”现象的出现，使得多视角图像拼接的效果较差.与传统运用运动估计方法实现运动物体跟踪的方法不同[12].该文在拼接时通过找出一条最佳缝合线，并在该线的两边取一帧图像的内容填充，来抑制“GHOST”现象发生.

动态规划算法是一种基于Bellman最优化原理，处理决策问题的优化算法：一个最优策略的子策略，对于它的初态和终态而言也必是最优的.如图3所示，最佳路线NM上有一点P，则PM也是最佳路线.

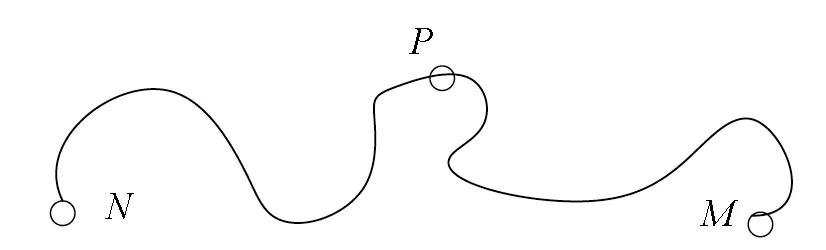
图3 最佳缝合线

在运用动态规划算法时，假设共有n阶段，则ri(Si,Xi)为第i阶段决策的数量指标，i阶段起点是St，i阶段终点和i+1阶段的起点为Xi，则动态规划就是求解值E

E=opt[r1(S1,X1)*…*rn(Sn,Xn)]

其中，“*”为运算符号，opt为max或min.在求解最短路径时，为了使各阶段相加和最小，opt取min，“*”取“+”.借鉴动态规划的思想，将上式作为求解策略指标值的准则式.首先从重叠区域的第一行出发，然后在该行上建立以每一个像素为起点的缝合线，最终找出最佳缝合线.具体步骤为：(1)初始化；(2)向下扩展计算过缝合线强度的一行，到最后一行为止；(3)从所得的所有缝合线的集合中选取强度值最小的为最佳缝合线.

2.3图像融合

图像融合就是将配准后的图像根据对准位置进行合并，并消除色彩的不连续性和噪声对图像的影响.常用的融合方法[13]有：(1)多分辨样条法；(2)加权平均法；(3)泊松融合法.多分辨率样条法由于涉及到高斯塔和拉普拉斯塔的构造问题，它是一种颜色融合方法，其具有计算量大、费时等缺点.加权平均法较简单，但易造成明显的拼接缝.泊松融合在选择融合区域时简单且方便，融合以源图像块内的梯度场作为指导，将融合边界上源图像和目标图像的差异平滑的扩散到融合图像块中，使得融合后的图像块融入到目标图像中时达到无缝的效果，且其色调和光照与目标图像保持一致.因此，该文采用泊松融合算法对拼接后的图像进行平滑处理.

3 实验结果与分析

该文的具体实验架构见表1.

表1 实验平台

通过相机拍摄多视角图像，在一台装有Windows7操作系统的PC机上，通过VisualStudio 2013和OpenCV2.4.10包进行仿真实验.

(1) 图像采用拍摄的两幅多视角图像进行实验，进行实验图像的像素为480*320px，具体实验结果如图4所示，其中改进ORB特征检测算法特征检测以及拼接后的图像分别为图4(c)以及图4(g)，可见基于改进ORB算法的多视角图像拼接效果良好.

(a) 原始图像

图4 多视角图像拼接实验结果

(2)实验证明改进ORB算法在提取特征点时误差较低，两个特征点最大间距和最小间距间该算法虽运行时间有小幅度提高，但ORB算子的分布较均匀.提取特征点间的误差比较见表2.

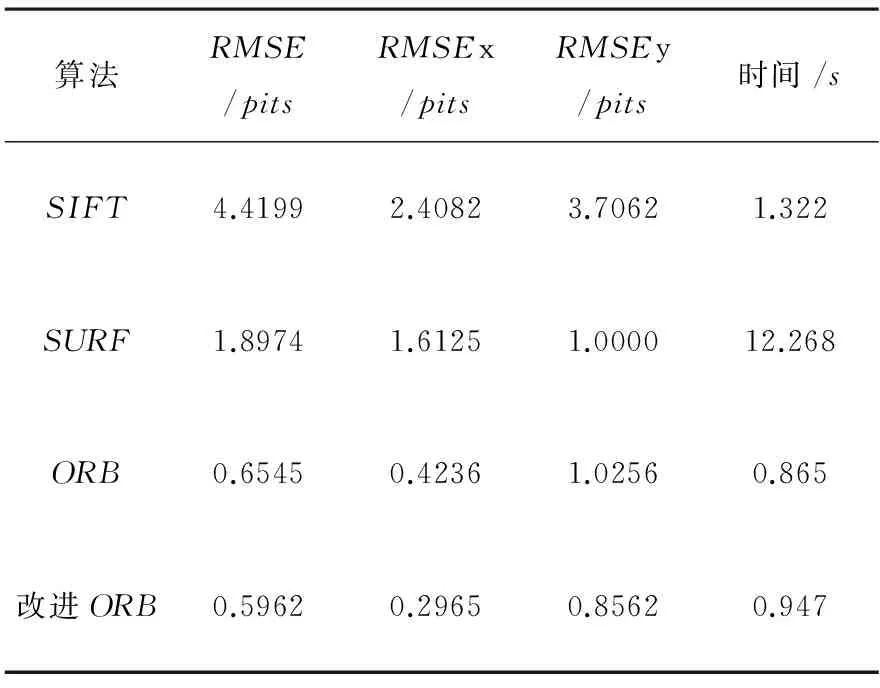
表2 各算法提取特征点误差比较

其中，RMSE为已知特征点坐标与检测出的特征点坐标间的整体均方根误差，X与Y向的均方根误差分别为RMSEx与RMSEy两个特征点的最大间距和最小间距比较见表3，可见ORB算法相比其他算法最大和最小间距的差距较小，且算法的运行时间相比ORB算法几乎一致.

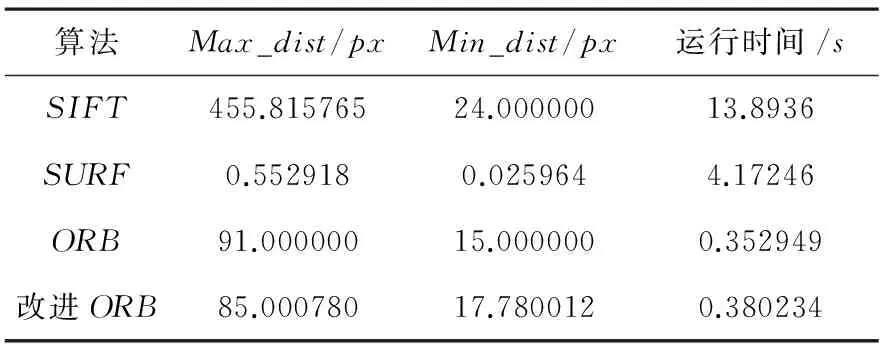
表3 特征点间最大和最小间距比较

实验结果表明，该文对ORB特征检测算法的改进具有较高的速度和精度，并通过动态规划算法寻求最佳缝合线和泊松融合算法对拼接后的图像进行平滑处理，有效的抑制了拼接裂缝和“GHOST”现象.

4 结论及展望

随着“全景视频”、“虚拟现实”等技术领域成为热议的话题，多视角图像拼接也成为人们关注的重点，多视角图像拼接的效果直接决定了产品的质量.仿真实验结果表明，该文提出基于改进ORB特征检测的多视角图像拼接方法，首先通过对ORB特征检测算法的改进，然后通过动态规划算法寻找最佳缝合线，最后运用泊松融合对拼接后的图像进行平滑处理的方法，有效的解决了图像拼接过程中存在的拼接速度以及存在的拼接裂缝和“GHOST”现象等问题.

[1] Ke Y,Sukthankar R.PCA-SIFT:A more distinctive representation for local image descriptors [C].Proceedings of the 2004 IEEE Computer Society Cinference on Computer Vision and Pattern Recognition.2004:506-513.

[2] Bay H,Tuytelaars T,Van Gool L.SURF:Speeded up robust features [C].European Conference on Computer Vision.2006:404-417.

[3] 索春宝,杨东清,刘云鹏.多种角度比较SIFT、SURF、BRISK、ORB、FREAK算法[J].北京测绘,2014(4):22-26.

[4] ALEC MILLS，GREGORY DUDEK.Image stitching with dynamic elements [J].Image and Vision Computing,2009,27(10):1593-1602.

[5] Rub lee E，Rabaud V，Konolige K，et al.ORB:an efficient alternative to SIFT or SURF[C].In International Conference of Computer Vision(ICCV),2011:2564-2571.

[6] Rosten E,Drummond T.Machine learning for highspeed corner detection[C].In European Conference on Computer Vision,2006:430-443.

[7] Calonder M，Lepetit V，Strecha C，et al.Brief:Binary robust ipendent elementary features[C].In European Conference on Computer Vision,2010:778-792.

[8] Rosin P L.Measuring corner properties[J].Computer Vision and Image Understanding,1999,73(2):291-307.

[9] Calonder' V,Lepetit M,Strecha C,et al.Brief:Binary robust independent elementary features[C].In European Conference on Computer Vision,2010:778-792.

[10] lindeberg T.Feature detection with automatic scale selection.International Journal of Computer Vision,1998,30(2):79-116.

[11] 杜京义,胡益民,刘宇程.基于区域分块的SIFT图像匹配技术研究与实现.光电工程,2013，40(08):52-58.

[12] PETER M，CHARLES V S，DAVID E T.Robust computer vision:an interdisciplinary challenge[J].Computer Vision and Image Understanding,2000(78):1-7.

[13] 黄立勤,陈财金.全景图拼接中图像融合算法的研究[J].电子与信息学报,2014,36(6):1292-1298.

Abstract:For the poor real-time multi perspective image mosaic method,and image mosaic is the existence of cracks of moving objects and the "GHOST" phenomenon,a multiple view mosaic image feature detection is proposed based on improved ORB in this paper.Through the improvement of the ORB algorithm makes the image feature extraction and matching accuracy and higher real-time performance,and by using the dynamic programming algorithm with low complexity to find the best suture line,the stitched image fusion are treated by the Poisson smoothing,which have a good inhibitory effect on splicing cracks multi view images and the phenomenon of “GHOST”.

Keywords:ORB algorithm; Multi view stitching; Dynamic programming algorithm; Poisson Fusion

(责任编辑：李家云)

MultiViewImageMosaicBasedonImprovedORBFeatureDetection

Li Wen,Li Xiaoyan

(YangEn University)

TP391.9

A

1000-5617(2017)02-0091-06

2016-11-15