基于小波变换的时间序列聚类

刘秀梅

(泉州理工学院)

基于小波变换的时间序列聚类

刘秀梅

(泉州理工学院)

针对传统以欧氏距离为相似性度量的K-均值聚类算法应用于时间序列数据上存在的时间轴偏移敏感性问题及以动态时间轴弯曲距离为相似性度量的高计算复杂性问题，提出基于小波变换的动态时间弯曲距离作为相似性度量方法，根据提取的小波低频系数与原时间序列之间的低能量差异来选择小波变换的尺度，能保证选取的特征在拥有尽量低的维数的同时保留时间序列主要信息.实验结果显示，基于小波动态时间弯曲距离的K均值聚类比基于欧氏距离的K均值聚类效果好，运行速度比动态弯曲距离快.

时间序列;小波变换;聚类

0 引言

传统在时间序列数据的聚类，以欧氏距离为相似性度量的K-均值聚类算法存在时间轴偏移敏感性问题;以动态时间轴弯曲距离为相似性度量存在高计算复杂性问题.该文提出基于小波变换的动态时间弯曲距离作为相似性度量方法，根据提取的小波低频系数与原时间序列之间的能量差异来选择小波变换的尺度，并通过小波变换提取时间序列的低频系数作为特征，然后用这些特征作为动态弯曲距离计算的输入值.这样既降低了时间序列的维数，降低了动态弯曲距离的计算复杂度，又保留了时间序列的主要特征.

1 小波动态时间弯曲距离

1.1动态时间弯曲距离[1]

设时间序列X=(x1,x2,…,xn),Y=(y1,y2,…,yn)，其长度分别为n和m.它们之间的动态时间弯曲距离定义为：

Ddtw(<>,<>)=0,

Ddtw(X,<>)=Ddtw(<>,Y)=∞,

(1)

Ddtw(X,Y)=d(x1,y1)+

其中<>表示空的时间序列，d(x1,y1)表示序列点xi和yi之间的距离.

1.2小波变换[2]

小波变换是一种将数据、函数或者算子分解成不同频率的成分，然后在与其尺度相匹配的分辨中研究各个成分的工具[3].可以总结为下面公式尺度函数(2)和小波函数(3)：

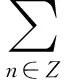
(2)

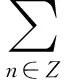
(3)

从公式(2)和(3)可以看出小波函数是通过尺度函数构造的，其中hn,gn是两个关键系数，分别定义为低通滤波器和高通滤波器.

1.3 Haar小波变换

Haar小波变换的尺度函数φ(t)和小波函数ψ(t)的定义为：

(4)

(5)

Haar变换可以被认为是对一个离散函数进行一系列的平均化和差分化操作.该文在每两个相邻的f(x)值之间计算其平均值和差值.

1.4小波变换不同尺度系数的选择

该文把某一尺度j的低频系数作为重构原始时间序列的特征，那么选择系数的关键就在于如何选择适当的尺度j.采用原始时间序列与小波特征的能量差异来选择适当的小波变换尺度[4].

提取的特征必须和原始的数据相似，要有一种适合的度量方法来衡量特征与数据之间的相异性，这里采用方差和来衡量时间序列和它的近似表示的差异.

定义1 方差和

(6)

因为对应j尺度的特征的长度比时间序列X小，因此不能直接通过公式计算.可以用低频系数Aj来重构一序列 ，然后计算X′和X之间的平方误差和.在正交小波变换中，能量是保持不变的，即E(X′)=E(Aj)，因此X′与X的能量差异等同于低频系数Aj与X之间的能量差异.这个属性使得不用重构X′，就能衡量Aj重构的X′与X之间的相似性.

定义2 能量

时间序列X={x0,x1,…,xn-1}，那么X的能量为

(7)

定义3 能量差异

时间序列X={x0,x1,…,xn-1}，经过j尺度的小波变换低频系数为Aj，那么Aj与X之间的能量差异为

(8)

X′可以通过在Aj后补0(补0后要保证重构X′的长度与X长度一样)重构而成.小波变换是保持能量不变的，因此j尺度的小波系数的能量应该和它重构的时间序列的能量是一样的.

E(X′)=E(Aj)和E(X)=E(Aj-1)+E(Dj-1)

当把X分解到j尺度时

因此，Aj和X的能量差异ED(X,Aj)就是在尺度j和高于j尺度的小波高频系数之和.

X的j尺度小波变换系数为{Aj,Dj,…,DJ-1}，X′的j尺度小波变换系数为{Aj,0,…,0}.因为欧氏距离同样在小波变换中保持不变，所以

因此X和X′的方差和等同于X和Aj的能量差异

SSE(X,X′)=ED(X,Aj)

(9)

对于小波变换从时间序列提取的特征中，尺度高的特征与尺度的低的特征相比保留更多的小波系数，维数也更高，因此随着小波变换的尺度的递减，SSE(X,X′)值会递增.理想尺度的特征应该同时具有较低的维数和较小的SSE(X,X′).

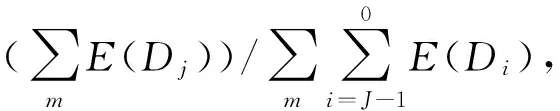
下面给出了小波变换选择低频系数的变换尺度的步骤：

(3)若找不到这样的尺度，选择尺度1作为小波系数提取的变换尺度.

2 基于小波变换的时间序列聚类

2.1K均值聚类

由于K均值的聚类结果受初始中心的选择影响很大，若随机选择序列作为初始聚类中心，那么聚类结果变化太大，这里采取两次K均值聚类，第一次采用欧氏距离度量方法，迭代收敛后产生的聚类中心作为第二次K均值聚类的初始聚类中心，第二次K均值聚类采用的是动态弯曲距离度量方法，这样能使聚类结果比较稳定.

2.2基于小波变换的时间序列聚类算法步骤

(2)选择小波变换提取特征的尺度j.

(5)用聚类中心c作为第二次K均值聚类的初始聚类中心.

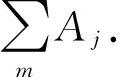
(7)算法收敛产生最终聚类结果.

2．3聚类结果评估方法

(1)已知真实聚类

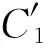
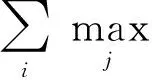
(10)

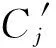
(11)

公式(11)中的|·|表示集合的势.

3 实验及结果分析

3．1实验环境及实验数据

在实验中，运行的环境是Pentium4 1.7GHz中的Matlab 6.5，实验数据采用keogh等人[6]提供的用于时间序列聚类的数据(见表1).

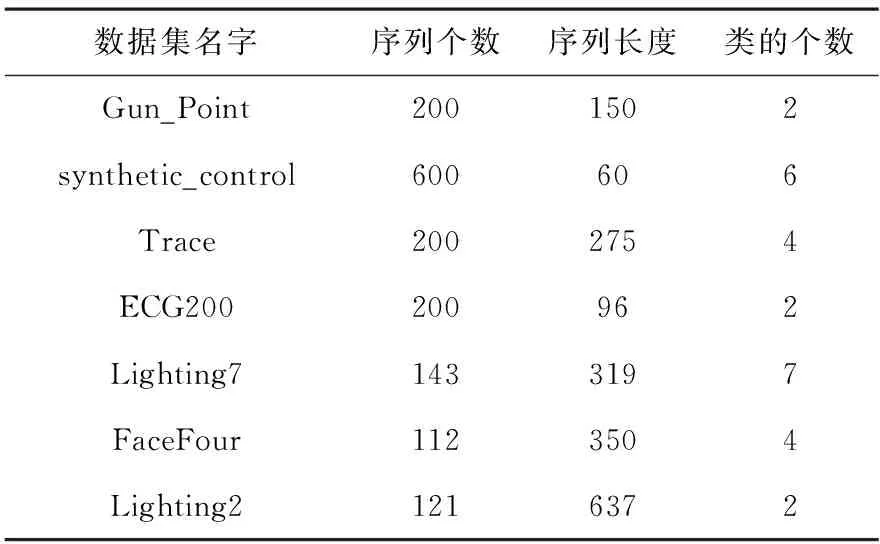
表1 聚类数据描述

3.2实验结果及分析

该文设计两个实验，实验一：计算出数据在不同Haar小波变换尺度下高频系数的能量，然后根据能量差异来选择小波变换的尺度.这样做的原因在于提取的时间序列的特征不仅要能提高聚类效率，而且不能丢失原时间序列的主要信息，否则聚类失去了实际意义.实验二：在该实验中，比较以下几种方法的聚类准确性和运行时间：①采用欧氏距离的kmeans聚类(简称EKC)；②采用动态弯曲距离的kmeans聚类(简称DKC)；③基于小波的欧氏距离的kmeans的聚类(简称WEKC)；④基于小波的动态弯曲距离的kmeans的聚类(简称WDKC).

(1)小波变换尺度的选择

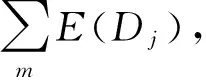
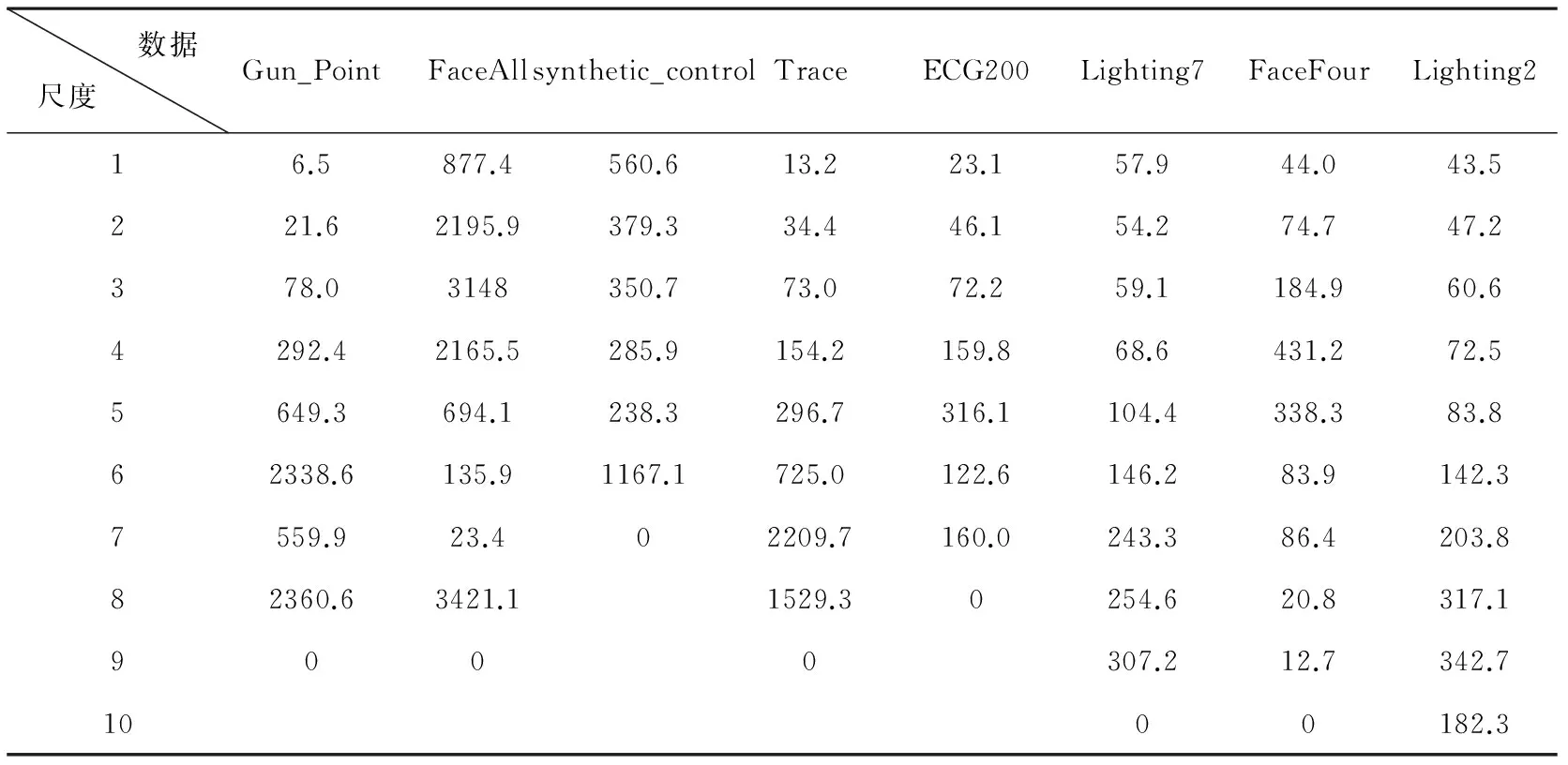
表2 不同小波变换尺度下高频系数的能量

表3 选择的小波变换尺度

(2)聚类结果比较

采用公式(10)(11)作为评价聚类结果的度量，近似度越高表示聚类的准确率越高，聚类方法的性能越好(见表4).

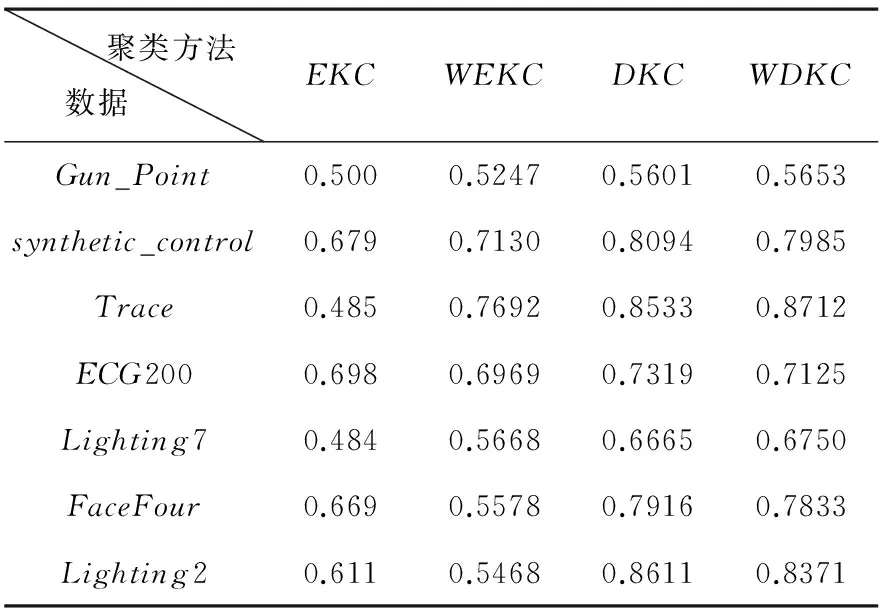
表4 聚类结果对比

从表4中发现小波变换对采用欧氏距离的kmeans聚类的聚类效果有适当的改进，改进的原因主要在于小波变换提取了时间序列中的低频系数并去除了高频系数中存在的噪声的影响，但改进不大，因为小波变换并没有解决欧氏距离对于时间轴弯曲的敏感性.而动态弯曲距离由于它支持时间轴弯曲，与欧氏距离方法EKC相比，对聚类效果的改善非常明显.

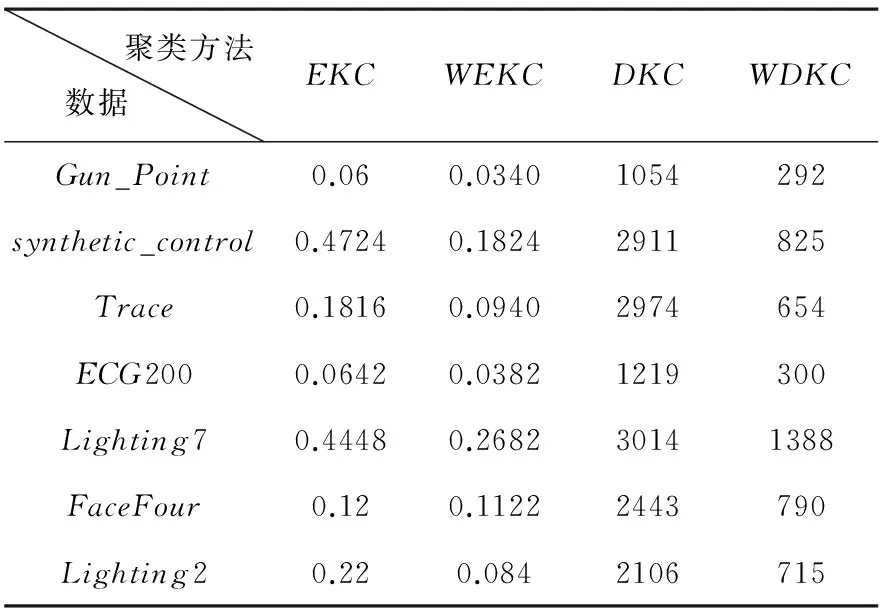
表5 运行时间对比 s

虽然动态弯曲距离可以解决时间轴弯曲的问题从而改善聚类质量,见表4，但由于其时间复杂性太高，运行时间过长,见表5.欧氏距离虽然在运行速度方面对动态弯曲距离有着明显的优势，但是不支持时间轴弯曲，使得其聚类质量并不高.而采用该文方法小波变换提取的特征系数在对时间序列降维的同时保留时间序列的主要信息，因此在不降低聚类的质量的同时明显改善了基于动态弯曲距离聚类的效率，也就是说基于小波变换的动态弯曲距离比普通动态弯曲距离效率提高达60%左右.

基于小波的动态弯曲距离能够很好的解决时间序列的时间弯曲问题，从而提高聚类的准确率，但是聚类的准确度还有提升的空间，距离度量方法还有提升的空间，现有的距离度量方法大多是把求解序列之间的相似度转化为序列中点与点之间的距离之和，很容易忽略了序列中点与点本身的联系.因此，下一阶段的研究方向是一种能更好地把序列中点与点之间的联系融合进距离度量方法.

[1] 曲文龙,张德政,杨炳儒.基于小波和动态时间弯曲的时间序列相似匹配[J].北京科技大学学报,2006(4):36-41.

[2] Chan K,Fu W.Efficient time series matching by wavelets[C].In:Proceedings of the 15th IEEE International Conference on Data Engineering,Sydney:IEEE,1999.126-133.

[3] Li Tao,Li Qi,Zhu Shenghuo,et al.A Survey on Wavelet Applications in Data Mining.SIGKDD Explorations,2003,4(2):49-68.

[4] Zhang H,Ho T B,Zhang Y,et al.Unsupervised Feature Extraction for Time Series Clustering Using Orthogonal Wavelet Transform[J].Journal Informatica,2006.

[5] Gavrilov M,Anguelov D,Indyk P,et al.Mining the stock market:Which measure is best?[J].In Proc of KDD’00,2000:487-496.

[6] Keogh E,Xi X,Wei L&Ratanamahatana C A.[EB/OL].The UCR Time Series Classification/Clustering Homepage:www.cs.ucr.edu/～eamonn/time_series_data/,2006.

Abstract:As Euclidean distance and its enlargement were sensitive to the shift of time axis and the defect of dynamic time warping in time complexity,a wavelet based dynamic time warping distance is proposed,which choose the wavelet coefficient by lower sum of squared errors between the features and the original time series,it can reduce the dimension of time series and preserve most information of the time series at the same time.TheKmeans for twice to limit the influence of choosing initial clustering center are applied.Euclidean distance for the first time and the final clustering center preparing for the initial clustering center of the second time are adopted,based danymic time warping distance.Expremental results show that the effect of clustering base wavelet based danymic time warping distance is better than that based Euclidean distance,and the run time of wavelet based danymic time warping distance is fast than dynamic time warping distance.

Keywords:Time series; Wavelet tranform;Clustering

(责任编辑：季春阳)

TimeSeriesClusteringBasedonWaveletTransform

Liu Xiumei

(Quanzhou Institute of Technology)

O211.61

A

1000-5617(2017)02-0013-05

2016-12-11