有16个极大子群的有限幂零群*

丁 磊，高宏一

(哈尔滨师范大学)

有16个极大子群的有限幂零群*

丁 磊，高宏一

(哈尔滨师范大学)

研究有限幂零群的极大子群的个数对有限群结构的影响，刻画了恰有16个极大子群的有限幂零群的结构.

有限幂零群;极大子群;Frattini子群;循环群

0 引言

极大子群是有限群的一类十分重要的子群，特别地，在有限幂零群的研究中有着非常关键的作用.而通过极大子群的个数来确定有限群的结构是研究有限群结构的一类重要的方法.现有一些结果如文献[1]中刻画了极大子群同阶类类数不大于2的有限群的结构，文献[2]中刻画了非正规极大子群同阶类类数等于2的有限群的同构类型，文献[3]刻画了极大子群同阶类类数等于3的有限群的同构类型，文献[4]中刻画了极大子群同阶类类数小于5的有限群的同构类型，文献[5-9]中刻画了恰有5-11个极大子群的有限幂零群的同构类型.该文研究了恰有16个极大子群的有限幂零群的结构.

1 预备知识

定义1[8]称群G的子群H为G的极大子群，如果H≤G,并且由H≤K≤G,可推出H=K或者K=G.

定义2[8]设G为有限群，若G≠1，令Φ(G)为所有极大子群的交；而若G=1，令Φ(G)=1.称Φ(G)为G的Frattini子群.

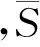
(2)M为G的极大子群当且仅当M/Φ(G)为G/Φ(G)的极大子群.

(3)M1和M2是G的不同的极大子群当且仅当M1/Φ(G)和M2/Φ(G)为G/Φ(G)的不同的极大子群.

引理2[5]设G是qn阶初等交换q-群，则G的qn(1≤m≤n)阶子群的个数为(qn-1)(qn-1-1)…(qn-m+1-1)/(qm-1)(qm-1-1)…(q-1).

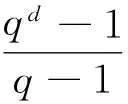
引理4[8]设G为有限幂零群且G=Q1×Q2×…×Qs为其Sylow子群的直积，令

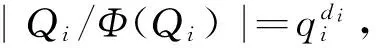
引理5[8]设G为有限群，则

(1)若G的所有极大子群共轭，则G为素数幂阶循环群.特别的，G有唯一极大子群.

(2)G恰有2个极大子群当且仅当G为2个不同的素数幂阶循环群的直积.

2 主要结果

定理1 设G是有限幂零群，则G恰有16个极大子群当且仅当G是下列群之一：

(i)G=Q1×Q2×…×Q16,其中Qi∈Sylqi(G)为循环群；

(ii)G=Q1×Q2×…×Q14，其中Qi∈Sylqi(G)，且Q1为2元生成2-群，Q2,Q3,…,Q14为循环群.

(iii)G=Q1×Q2×…×Q13，其中Qi∈Sylqi(G)且Q1为2元生成3-群，Q2,Q3,…,Q13为循环群.

(iv)G=Q1×Q2×…×Q11，其中Qi∈Sylqi(G)，且Q1为2元生成5-群，Q2,Q3,…,Q11为循环群.

(v)G=Q1×Q2×…×Q11，其中Qi∈Sylqi(G)，且Q1为2元生成2-群，Q2为2元生成3-群，Q3,…,Q11为循环群.

(vi)G=Q1×Q2×…×Q10,其中Qi∈Sylqi(G)，且Q1为3元生成2-群，Q2,Q3，…，Q10为循环群.

(vii)G=Q1×Q2×…×Q9，其中Qi∈Sylqi(G)，且Q1为2元生成7-群，Q2,Q3,…,Q9为循环群.

(viii)G=Q1×Q2×…×Q9，其中Qi∈Sylqi(G)，且Q1为2元生成2-群，Q2为2元生成5-群，Q3，…,Q9为循环群.

(ix)G=Q1×Q2×…×Q8，其中Qi∈Sylqi(G)且Q1为2元生成3-群，Q2为2元生成5-群，Q3,…,Q8为循环群.

(x)G=Q1×Q2×…Q7，其中Qi∈Sylqi(G)，且Q1为2元生成2-群，Q2为2元生成7-群，Q3,…,Q7为循环群.

(xi)G=Q1×Q2×…×Q7,其中Qi∈Sylqi(G)，且Q1为3元生成2-群,Q2为2元生成3-群，Q3,…,Q7为循环群.

(xii)G=Q1×Q2×…×Q6，其中Qi∈Sylqi(G)，且Q1为2元生成3-群，Q2为2元生成7-群，Q3,…Q6为循环群.

(xiii)G=Q1×Q2×…×Q6，其中Qi∈Sylqi(G)，且Q1为2元生成2-群，Q2为2元生成3-群，Q3为2元生成5-群,Q4,Q5,Q6为循环群.

(xiv)G=Q1×Q2×…×Q5，其中Qi∈Sylqi(G)，且Q1为2元生成11-群，Q2,Q3,Q4,Q5为循环群.

(xv)G=Q1×Q2×…×Q5,其中Qi∈Sylqi(G)，且Q1为3元生成2-群，Q2为2元生成5-群,Q3,Q4,Q5为循环群.

(xvi)G=Q1×Q2×Q3×Q4，其中Qi∈Sylqi(G)，且Q1为3元生成3-群，Q2,Q3,Q4为循环群.

(xvii)G=Q1×Q2×Q3×Q4，其中Qi∈Sylqi(G)，且Q1为2元生成5-群，Q2为2元生成7-群,Q3,Q4为循环群.

(xviii)G=Q1×Q2×Q3，其中Qi∈Sylqi(G)，且Q1为2元生成2-群，Q2为2元生成11-群,Q3为循环群.

(xix)G=Q1×Q2×Q3,其中Qi∈Sylqi(G)，且Q1为3元生成2-群，Q2为2元生成7-群,Q3为循环群.

(xx)G=Q1×Q2，其中Qi∈Sylqi(G)且Q1为2元生成3-群，Q2为2元生成11-群.

证明充分性显然，下证必要性.

由于G为幂零群，所以G=Q1×Q2×…×Qs，,其中Qi∈Sylqi(G)，q1

(1)若s=16,则每个Qi只能有1个极大子群，于是di=1,即Qi为素数幂阶循环群.因此，G为16个不同素数幂阶循环群的直积，为定理中(i)型群.

(2)若s=15，则至少有一个di≥2，不妨设d1≥2，于是Q1为非循环，由引理4，Q1至少有3个极大子群，从而G至少有17个极大子群，矛盾.

d1=2,q2=3,d2=2,即Q1为2元生成2-群，Q2为2元生成3-群，Q3,…,Q11为循环群，为定理中(v)型群.

[1] 施武杰.极大子群同阶类类数不大于2的有限群[J].数学年刊：A辑，1985(5):532-537.

[2] 李世荣.非正规极大子群同阶类类数等于2的有限群[J].数学学报,1990(3):388-392.

[3] 黎先华.极大子群同阶类类数等于3的有限群[J].数学学报,1994(1):108-115.

[4] 王立中.极大子群个数<5的有限群[J].首都师范大学学报,2000,21(3):10-13.

[5] 游兴中，王香芬，陈为敏.恰有5个极大子群的有限群[J].吉首大学学报：自然科学版,2010,31(5):8-10.

[6] 游兴中，朱伟华，刘峥.恰有6个极大子群的有限群[J].吉首大学学报：自然科学版,2011,32(3):1-3.

[7] 游兴中，刘峥，朱伟华.恰有7个极大子群的有限群[J].吉首大学学报：自然科学版,2011,32(5):11-15.

[8] 王克瑜，郭继东.恰有9和10个极大子群的有限幂零群[J].兰州文理学院学报：自然科学版,2014,28(3):23-28.

[9] 刘春娟，钱方生.恰有11个极大子群的有限幂零群.哈尔滨师范大学:自然科学学报,2015,31(1):28-30.

Abstract:In this paper,the number of maximal subgroup to influence the structure of groups is studied,the structure of the finite nilpotent group which just having sixteen maximal subgroups is described.

Keywords:Finite nilpotent group; Maximal subgroup; Frattini subgroup; Cyclic group

(责任编辑：季春阳)

FiniteNilpotentGroupofJustHavingSixteenMaximalSubgroups

Ding Lei，Gao Hongyi

(Harbin Normal University)

O152.1

A

1000-5617(2017)02-0001-04

2017-02-08

*黑龙江省自然科学基金面上项目(A201412)