矩形截面弹簧成形过程有限元仿真分析

北京工商大学 魏景辉 项辉宇

学术研究

矩形截面弹簧成形过程有限元仿真分析

北京工商大学 魏景辉 项辉宇

矩形截面弹簧的特性曲线更接近于直线，较圆形截面弹簧更具有优势，但是矩形截面弹簧有芯轴卷制成形过程加工工艺复杂，无论是冷卷成形还是热卷成形，都可能有缺陷产生，比如热卷时出现褶皱。为了探究缺陷产生的原因，可以采用MSC.Marc有限元仿真分析的方法，模拟仿真矩形截面弹簧卷制的过程，对仿真结果进行分析。本文阐述了有限元仿真分析的过程，并分析了弹簧设计参数矩形截面的长宽比对成形质量的影响。

矩形截面弹簧 有芯轴卷制 有限元仿真 长宽比

我国对矩形截面弹簧研究起步较晚，80年代才逐渐开始研究，而且到目前为止，加工工艺较国外也比较落后，近年来，随着有限元软件的推广，采用有限元分析的方法开始研制矩形截面弹簧卷制的新工艺，李蕾[1-2]等人应用ANSYS有限元分析软件分析了整枝机用的矩形截面弹簧，初步提出了一种矩形截面扭转弹簧的有限元分析方法，并给出了基本的分析思路，为以后矩形截面扭转弹簧的设计和优化奠定了基础。于洋[3]等人采用等效组合弹簧的方法设计了钻井封隔器用的矩形截面弹簧，并利用SolidWorks进行建模，在ABAQUS中进行有限元分析，获得了矩形截面弹簧的轴向刚度。国外学者也在研制矩形截面弹簧，比如日本电气通讯大学的学者[4]设计了矩形截面螺旋弹簧[7]作为一些机器人关节的联合机构。矩形截面弹簧还处于发展期。

本文采用强大的非线性有限元分析软件MSC.Marc仿真分析，模拟弹簧卷制的过程，得到应力应变分布情况，然后改变矩形截面弹簧截面的长宽比，利用控制变量法，探究长宽比与弹簧卷制成功后的应力应变之间的关系；然后根据数据点作曲线拟合并分析，优化弹簧卷制工艺，提高弹簧卷制工艺水平，达到提高产品质量和减少试制成本的目的，为矩形截面弹簧的设计加工制造提供参考。

0 弹塑性成形基本理论

矩形截面弹簧在机床上卷制过程的实质是弹塑性成形问题，目前解决非线性弹塑性成形问题的基本理论主要有屈服准则、全量理论、增量理论和材料弹塑性本构关系[5]。

对弹簧的弹塑性成形过程进行有限元分析一般采用米塞斯屈服准则，其数学表达式如下：

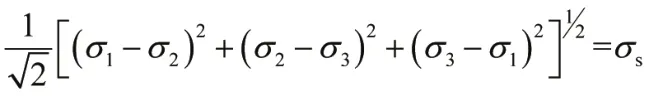
式中σ1、σ2、σ3为三个主应力。在简单加载条件时，由理想状态下的弹塑性增量理论公式，可求出应力增量与应变增量的对应关系为：

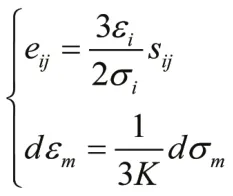
式中，eij—应变偏张量；εi—材料内一点应变；σi—材料内一点应力。Sij—应力偏张量；dεi—应变增量；dσi—应力增量；K —体积弹性模量。

上式就是材料在塑性状态下形变理论公式，即塑性本构方程。由相关文献可知全量理论属于增量理论的一种特殊情况，如果设置简单加载条件的话，这两种本构关系的表达式是一样的。

在弹性变形阶段，材料所受应力与应变之间是符合胡克定律的，即为弹性阶段的本构方程；在矩形截面弹簧卷制过程中，既有弹性变形，又有塑性变形，因此在加载过程中，弹簧方钢发生塑性变形，服从塑性本构关系；其余没有加载过程中，弹簧方钢都是服从弹性本构关系的。

1 弹簧参数的设定与卷制过程的仿真

本文采用有芯轴的卷制方式，弹簧在机床上卷制成形的过程如图1所示，芯轴装在主轴卡盘上与主轴一起旋转。弹簧方钢被咬紧装置卡在芯轴上，芯轴旋转，送料装置沿芯轴的轴向移动行程使弹簧方钢在芯轴上卷制成螺旋线状，形成矩形截面圆柱螺旋压缩弹簧。

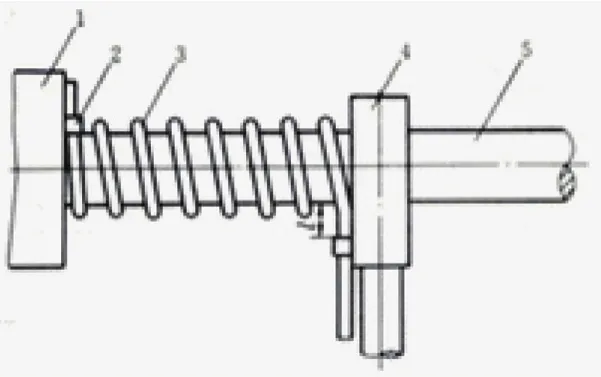
图1 有芯轴卷簧示意图

根据上述矩形截面弹簧成形过程可以分析得知，弹簧的卷制是高度复杂的非线性问题[6]，涉及到几何非线性问题、材料的非线性问题以及成形过程的非线性问题，因此，采用传统的材料力学和弹性力学很难设计出高精度弹簧。采用有限元分析方法对矩形截面弹簧卷制过程进行数值仿真分析应运而生。

本文应用高级非线性分析软件MSC.Marc有限元分析软件对此非线性问题进行模拟分析。

经前期矩形截面弹簧设计,本文拟进行仿真模拟的过程中需要的设计参数,如表1所示。

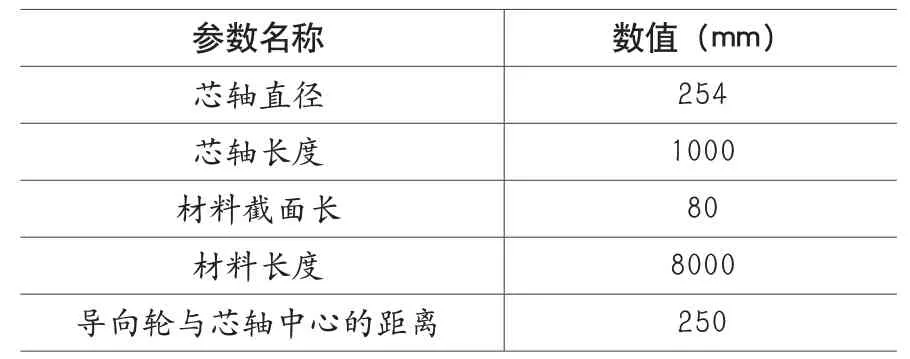
表1 弹簧卷制过程需要的参数

1.1 有限元模型的建立

对矩形截面弹簧进行有限元仿真分析的第一步就是建立几何模型，文献[8]表述可以综合应用UG、Hyper Mesh和MSC.Marc进行有限元仿真，因此本文通过UG NX8.0完成三维模型的建立，根据表1中尺寸以及矩形截面的宽的三种不同尺寸，分别对弹簧方钢、芯轴、咬紧装置、导向装置和加紧装置进行三维实体建模。

有限元分析的第二步就是将实体模型离散为有限个实体单元，也即进行实体网格的划分，网格划分应用具有强大分网功能的HyperMesh软件，将弹簧方钢的实体模型导入到Hyper Mesh软件中，把模型中没有用的线条进行删除处理，然后设置单元尺寸为8mm，选择六面体实体网格进行划分，对宽边为30mm的弹簧方钢模型共划分为40000个单元，并导出MSC.Marc可以识别的.DAT格式文件。

最后将分网后的模型通过通用接口直接导入到MSC.Marc中，这样就完成了弹簧方钢的有限元模型建立。整个有限元分析过程的模型的其余部分，直接在MSC.Marc中导入UG NX的标准格式.PRT作为NURBS曲面。所建立的有限元模型和网格划分情况如图2所示。

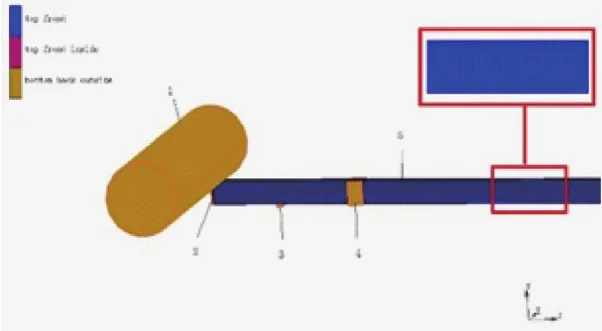
图2 有限元仿真模型

1.2 仿真模型的简化说明

（1）根据弹簧卷制的基本过程，本文所建立的有限元模型与理论过程是不一样的，卷制的实际过程是芯轴转动，弹簧方钢未卷入部分平动，整个的相对移动就是螺旋线；而本文建立的模型中芯轴既有进给运动又有旋转运动，然后卷入的方钢模型随芯轴平动。两个过程的相对运动是一样的，都是为了形成螺旋线，因此这样简化为正确的。

（2）整个卷制加工过程中弹簧方钢是在高温下进行的，卷制过程时间不长，因此产生的热效应和弹簧与周围的热传递是忽略不计。

（3）本文中对弹簧实际卷制过程中的导向装置与加紧进装置行了简化，由实际分析得知，导向装置在卷制过程中只对材料起到支撑并导向的作用，而如果直接按实际轮状进行建模的话，材料与导向轮之间的接触是非常复杂的，这样不仅会增加计算时间，极可能出现计算不收敛的情况。因此，本文将导向轮简化为一根支撑杆；对于加紧装置的简化也是由于同样的原因，而且加紧装置的作用就是防止材料在卷制过程中上下左右摆动，将加紧轮简化为块状加紧装置，这样就只有面与面之间的接触关系了。

1.3 仿真过程

按照有限元分析的一般步骤与MSC. Marc的软件分析特点[9]，在Marc环境中建立有限元模型之后，要给有限元模型赋予材料属性。本文选用的材料是40Cr合金钢材料，其材料属性如表2所示，按照表中数据将材料属性定义完毕，并将其赋给弹簧方钢的每个单元即可。

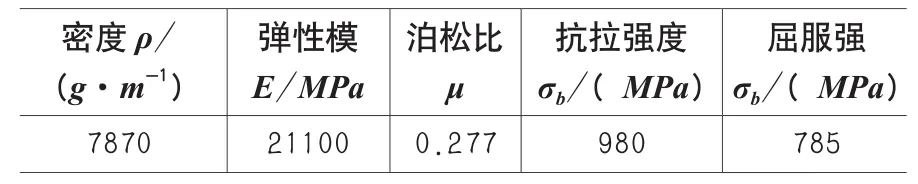
表2 40Cr材料属性

材料属性定义完之后，将模型中的弹簧方钢模型设置为变形体（Meshed(Deformable)）。实际卷制过程中，弹簧方钢与各装置之间是有摩擦存在的，因此在仿真过程中假设摩擦系数始终保持不变，并采用库伦摩擦，并在旧特性（Obsolete Properties）中设置摩擦系数为0.3。有限元模型的其余部分包括芯轴、导向装置、咬紧装置和加紧装置设置成刚体（Geometric），并设置芯轴与咬紧装置的速度，芯轴的速度设置如图3所示，既有沿x轴的平动，又有绕x轴的转动。

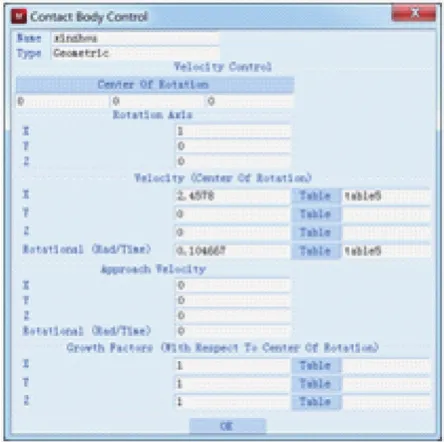
图3 速度设置

接着要为接触关系建立接触表，在MARC中有两种接触方式，分别是Touching和Glue，在本次仿真模拟中要将弹簧方钢与芯轴、弹簧方钢与导向装置、弹簧方钢与加紧装置之间的接触设置为T接触，将弹簧方钢与咬紧装置之间的接触设置为G接触，设置结果如图4所示。

本文仿真的是高温有芯轴热卷弹簧的卷制过程，因此需要设置初始条件（Initial Conditions），在MSC2013中，初始温度条件是加载到节点上的，因此定义Node Temperature为950℃。设置结果如图5所示。

最后要进行分析任务的创建，将接触、初始条件、工况创建到分析任务中，并添加所要分析的内容，检查整个过程中是否有错误，最后提交计算，待计算完成之后查看结果，提取数据作分析。

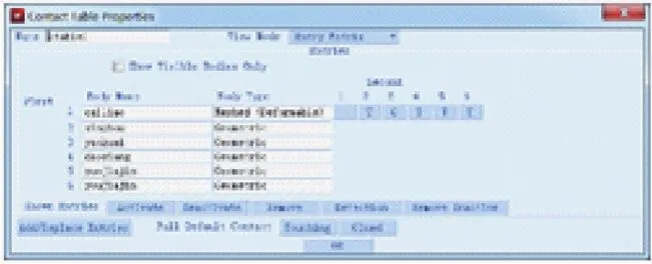
图4 接触表设置

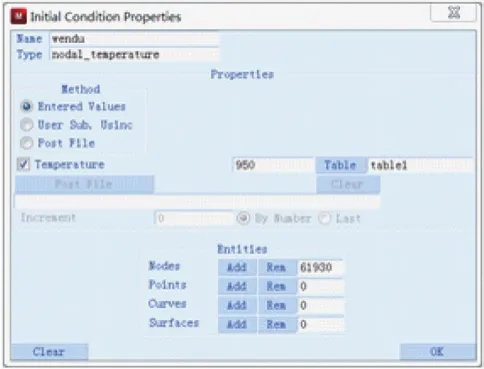
图5 初始温度设置

1.4 仿真过程流程图

根据以上仿真分析过程以及MSC.MARC软件的特点，仿真过程流程图如图6所示。

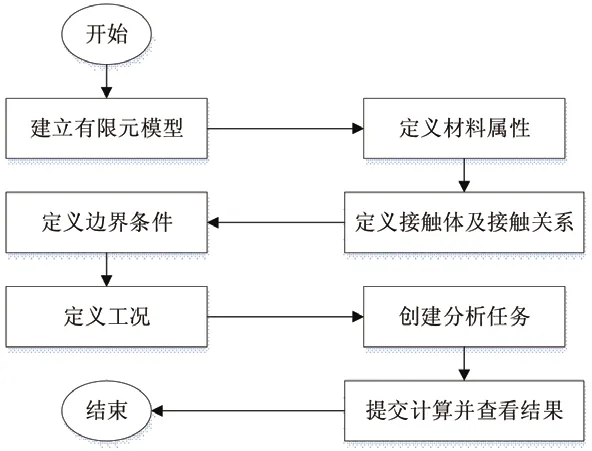
图6 有限元仿真流程图

2 仿真结果与分析

按照上述仿真分析的一般过程，将有限元模型提交计算得到后处理模型，其等效米塞斯应力分布图和等效塑性变形图如图7所示。

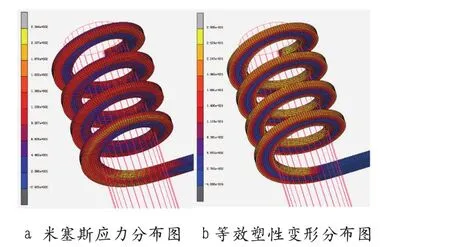
图7 仿真结果

图7的仿真结果为矩形截面宽为30mm时的计算结果，从a图可以看出，矩形截面弹簧卷制成功以后，应力分布较为均匀，且成形以后的部分的等效米塞斯应力值几乎不再改变。从b图可以看出，矩形截面弹簧内圈受压，外圈受拉，而中性面等效塑性变形较小，与弹簧卷制理论相一致，因此可以证明该仿真的正确性。

改变矩形弹簧截面的宽度为25mm和35mm，分别重新按照仿真流程建立有限元模型进行仿真计算，得到仿真结果等效米塞斯应力分布图分别如图8所示。

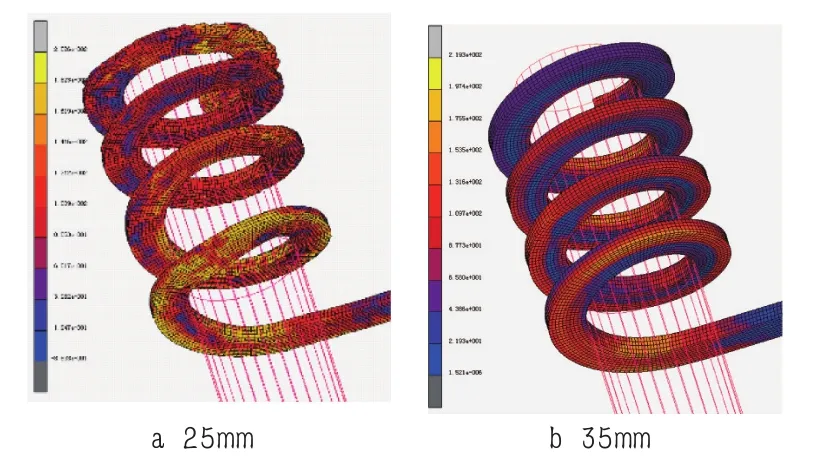
图8 米塞斯应力分布图

上图中可以看到当矩形弹簧截面宽为25mm的时候，弹簧卷制已经出现了明显的褶皱变形缺陷，而截面宽为30mm和35mm的都很光滑，没有缺陷产生，将成形质量进行量化，取矩形截面弹簧方钢边缘四个点为特征点，分别是刚开始就进入卷制的点A，加紧装置之前的点B，和之后先通过加紧装置再进入卷制且距离加紧装置较近的点C，以及先通过加紧装置再进入卷制且距离加紧装置较远的点D，特征点位置分布图如图9所示。分别在后处理结果中提取这三点在卷制过程中等效米塞斯应力变化数据，再根据数据进行曲线拟合，其拟合曲线如图10所示，通过对比分析得知在一定长宽比范围内，长宽比越小，卷制过程中弹簧方钢所受应力越小，弹簧成形质量越好，通过这个结论可以为矩形弹簧的设计提供参考，在条件允许的情况下，尽量选择较小矩形截面长宽比。

3 结论

（1）仿真过程中的模型简化是正确的、可行的。

（2）弹簧卷制过程的仿真与真实情况下的弹簧卷制过程所受应力分布一致，可以通过模拟仿真的方法为进行矩形截面弹簧的设计与加工工艺的制定提供依据。

图9 特征点位置分布图

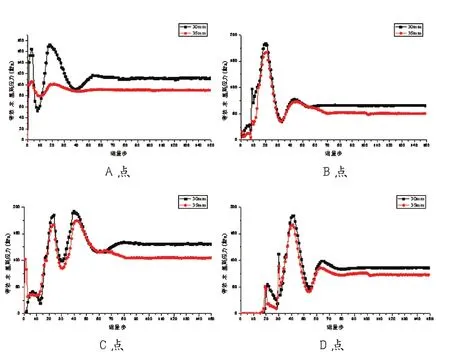
图10 特征点等效米塞斯应力曲线图

（3）考虑到加工工艺的制定，矩形截面弹簧设计过程中在条件允许的情况下应尽量选择较小的长宽比，若选取的长宽比太大，则加工条件变得复杂，甚至很难加工制造或不能卷制成形。

[1]李蕾.整枝机传动机构中矩形截面弹簧的研究[D]. 北京林业大学, 2008.

[2]李蕾, 霍光青, 王乃康等.整枝机传动装置中矩形截面弹簧的研究[J].林业机械与木工设备, 2007, 35(11):21-24

[3]于洋, 张怡.钻井封隔器用矩形截面弹簧的设计与校核[J].制造业自动化, 2015, 37(14):107-109

[4]Tsubouchi, Tsubasa, Takahashi, Kazuhito, Kuboki, Takashi.Development of coiled springs with high rectangular ratio in cross-section[J].Procedia Engineering, 2014, 42(10):574-579

[5]王文骞.弹簧数控卷绕成形及回弹数值分析[D]. 河南科技大学, 2015.

[6]王玉梅，陈火红，王军，等.基于Marc的螺旋钢弹簧卷制过程的仿真分析[J].计算机辅助工程, 2013, 22(S1):427-430

[7]董志波等.MSC.Marc工程实例详解[M] 北京:, 人民邮电出版社:, 2014

[8]蒋学武，吴新跃，朱石坚.综合应用UG，HyperMesh和MSC Marc软件进行有限元分析[J].计算机辅助工程, 2007,16(02):11-14

[9]冯超, 孙丹丹, 陈火红.全新Marc实例教程与常见问题解析[M] 北京:, 中国水利水电出版社:, 2012.