以问题为核心上好初中几何复习课
2017-09-29刘长良
刘长良
以问题为核心上好初中几何复习课
刘长良
问题是思维的核心,精心设计一个好的问题,运用恰当的方法,能引领学生轻松愉快地串连相关知识点、串联形异质同的问题,解决复杂的相关问题和生活中的实际问题,如复习“圆的有关性质”时,可以运用如下方法。
一、寻求多解,串联知识方法
例题:如图已知:△ABC是⊙O的内接三角形,AD是高,AE是⊙O的直径,求证AB·AC=AD·AE
解法一:连结BE,∵AE是⊙O的直径,∴∠ABE=∠ADC=90°,又∵∠E=∠C,∴△ABE∽△ADC,∴,∴AB·AC=AD·AE
反思解题过程回顾所用知识点和解题技巧:圆周角定理及其推论、圆心角定理、垂径定理、相似三角形判定及性质;添加辅助线技巧;作弦心距、构成直径所对的圆心角是常用辅助线作法。
二、探究变式,串联形异质同问题
根据问题特征,变化图形,串联形异质同问题。通过问题变式和解答,不但能使学生迅速解答难度较大的问题,而且能有效培养学生探究发现问题的能力,激发学生兴趣。针对以上问题作下列变式:
变式一:如图2已知:△ABC是⊙O的内接三角形,AD是高,BE是⊙O的直径,
求证:AB·AC=AD·BE
变式二:如图3已知:△ABC是⊙O的内接三角形,以A为圆心作⊙A,使⊙A与BC边相切于点D,⊙A的半径为r,作⊙O的直径AE,
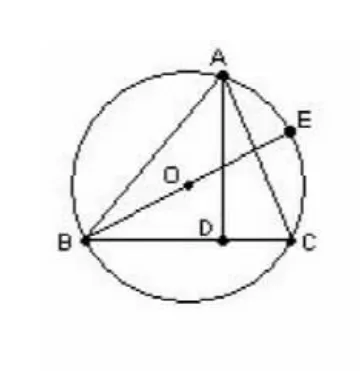
图2

图3

图4
求证:AB·AC=AE·r。
变式三:如图4已知:△ABC是⊙O的内接三角形,以A为圆心作⊙A,使⊙A与BC边的延长线相切于点D,⊙A的半径为r,作⊙O的直径AE,
求证:AB·AC=AE·r。
三、运用结论,迅速解决复杂问题
1.解决函数最值问题
如图5、已知:△ABC是⊙O的内接三角形,AD是高,AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x。
(1)求y与x的函数关系式;
(2)当x取何值时,⊙O的面积最大,并求⊙O的最大面积。
2.设计圆半径的测量方案

图5

图6
图6 所示的是一个残缺的机器轮子,现在手中只有标有刻度的尺子,请你设计测量机器轮子半径的方案,并求出轮子的半径。
上数学复习课时,设计一个好的数学问题,让学生尽可能多的寻求多种解法,针对问题广泛联想,探究变式,注重结论在相关问题中的应用,能调动学生的学习积极性,大大提高复习效率,有效培养学生的创造性思维能力。
(作者单位:山东蒙阴县孟良崮中学)
