一种双向曲率板成型应变分布的力学计算方法

胡昌成，赵 耀，袁 华

(华中科技大学 船舶与海洋工程学院，湖北 武汉 430074)

一种双向曲率板成型应变分布的力学计算方法

胡昌成，赵 耀，袁 华

(华中科技大学 船舶与海洋工程学院，湖北 武汉 430074)

在双向曲率板线加热成型及滚压成型的工艺设计研究中，一项十分重要的工作就是依据所需目标形状计算应变分布并以此确定加工路径和工艺参数，因此应变分布计算的精度直接影响到加工路径和工艺参数的准确性。本文介绍了一种基于力学方法的应变分布计算方法，首先对平板施加节点位移场进行弹塑性计算，由于存在回弹现象，需对节点位移场进行反变形修正，本文将得到的形状与目标进行对比后，再利用两者偏差对位移场进行迭代修正，直到两者偏差满足精度要求，最后将得到的应变场以初应变的形式输入到平板模型上，用初应变法的结果对应变的计算方法进行验证，证明该方法的精度，为后续加工路径和工艺参数的准确确定提供基础。

双向曲率板；应变分布；力学方法；面内应变；弯曲应变

0 研究背景

船舶建造等行业中常用的曲面板一般是通过机械加工或者线加热成型的方式得到，从力学成型机理上看，曲面板的成型是将弯曲应变和（或者）面内应变施加到平板上得到的，对于单向曲率板只需要弯曲应变即可得到，对于双向曲率板则需要弯曲应变和面内应变的共同作用。在实际加工中，单向曲率板可以用三辊弯板机等设备直接加工得到，对于双向曲率板则需要借助于线加热成型、线滚压成型、模压成型等方式实现目标形状板的加工。

线加热成型和线滚压成型是船舶外板等双向曲率板建造中十分常用的成型方法，其原理是通过热源或滚轮的移动在被加工板上逐渐产生塑性变形，通过将局部范围内的变形扩展至整条加工路径上最终产生整体的变形，其整体形状是通过对局部变形的控制来实现的，由于其整体变形与加工路径、工艺参数之间没有明显的关系，很难直接通过所需的目标形状确定加载路径和工艺参数。为了实现双向曲率板成型的自动化，需要根据所需的目标形状确定对应的加工路径和工艺参数，大量科研工作者的研究[1 – 3]表明，线成型加工产生的应变分布与加工路径之间具有明显的关系：面内应变及弯曲应变的主应变方向与加工路径垂直。根据这一特性，提出了一种自动化线成型的方案[3 – 5]：首先根据目标形状计算应变分布，再根据应变确定加工路径的位置，最后确定相应的工艺参数。

在上述方案中，第1步就是根据所需目标形状计算应变分布，因此计算得到的应变分布精度直接影响到后续确定加工路径和工艺参数的准确性。根据目标形状计算应变分布的方法主要有力学展开法和微分几何方法，Letcher[6]通过求解普遍的含高斯曲率的possion方程得到应变场，Shin[7]强调了面内应变的作用，提出了面内应变的计算方法；Yu[8]通过求解一个约束非线性规划方程得到最小应变场的分布；张雪彪[9]利用参数曲面表达的方法进行了帆形板的展开。然而Cheng[1]指出利用微分几何方法通常只能得到面内应变分布，对于弯曲应变则很难得到，而基于力学的展开方法则可以同时准确得到这2种应变的分布情况。Ueda[3 – 5]利用大变形弹性有限元法计算从初始平板到最终形状所需的应变，可是并没有给出具体的求解过程；Liu[10]将目标形状板放置于2块刚性体平板之间，目标形状板与平板之间无摩擦，两平板之间距离不断减小直至等于目标形状板的板厚，此方法得到的应变分布与所需的应变分布符号相反，并且没有考虑回弹对应变结果的影响。

本文介绍了一种基于迭代修正的力学方法进行应变分布的求解，通过弹塑性有限元方法计算得到应变的分布，同时考虑回弹的影响，利用迭代修正法对目标形状施加反变形以减少回弹的影响，能够快速准确地计算得到成型双向曲率板所需的应变分布，最后以初应变法计算得到的应变分布所对应的变形形状，用初应变法的结果对应变分布的计算方法进行验证，证明了应变计算方法的准确性。

1 总体方案

本文介绍的计算应变分布力学方法按照图1所示的流程实现：

1）首先根据所需的目标形状，对目标形状曲面进行三维曲面拟合，并根据拟合的结果计算有限元模型中每个节点的位移场；

2）将得到的位移场以节点位移载荷的形式施加到弹塑性模型上，由于平板模型在发生大挠度变形的同时会伴随着板长和板宽方向的位移，因此在施加节点位移时只施加板厚方向的位移，在板长和板宽方向则处于自由状态，同时对整块板进行刚体位移约束；

3）利用Abaqus有限元软件进行弹塑性计算，进行平衡迭代计算出平板的变形，在此步骤中会计算回弹对变形的影响，得到的应变场和变形场均为回弹后的结果；

4）将得到的变形结果与所需形状进行对比，由于两模型存在着坐标不一致等问题，本文利用基于最小二乘的原理对模型进行空间坐标变换，实现两模型坐标的统一，并计算两者之间的总体偏差；

5）若总体偏差满足精度要求，则直接从有限元计算结果中提取应变结果，若不满足精度要求，则根据步骤3中得到的变形与所需形状之间的偏差对位移场施加反向变形，重新进行步骤1～步骤4中的过程，直至偏差满足精度要求。

2 计算实例

2.1 模型建立

以目标形状为鞍形的平板成型为例，对力学方法计算应变分布的过程进行详细说明。初始平板的尺寸为2 000 mm×1 000 mm×20 mm，杨氏模量为2.1×1011Pa，泊松比为0.3，弹塑性属性参照1010 steel钢，为了完整地得到整块板的应变分布，利用实体单元对模型进行网格划分，板厚方向划分4层网格，网格大小为40 mm×40 mm×5 mm，建立的有限元模型及网格划分如图2所示。

2.2 位移场施加

本文以鞍形板的成型为例，定义鞍形板的目标形状为z=x2/4–y2/9，如图3所示。

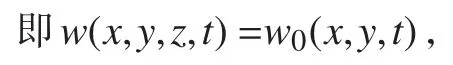
2.3 弹塑性计算

本文使用Abaqus有限元软件进行弹塑性的数值计算，Abaqus软件可以根据输入的节点位移载荷自动进行平衡迭代求解变形结果，设置2个分析步：第1步施加位移载荷进行弹塑性计算；第2步将位移载荷卸载，此时被加工板会由于残余应力的作用而发生回弹作用，在回弹后所得到的形状与目标形状不同。在回弹前后板的塑性最大主应变分布如图5所示，从图中可以看出，回弹前后被加工板的塑性应变分布几乎不变，即回弹前后2种状态的变形场对应着同一种塑性应变状态，分析其原因，是由于在回弹前，板中存在残余应变，节点受外部载荷作用，此时板中的应变分布不协调，在此状态下的应变分布所对应的形状是回弹后的板形状，因此若根据此塑性应变进行加工路径和工艺参数的确定，则与目标形状之间存在着偏差。

2.4 结果对比

图6为弹塑性计算得到的回弹后形状与目标形状对比结果图，虚线表示回弹后的变形形状，实线表示目标形状，从图中可以看出由于回弹的影响，导致所得到的形状与目标形状存在着较大的差别，同时弹塑性模型的坐标与目标形状的坐标不在同一个坐标系中，所以在进行结果对比之前必须进行坐标匹配，本文使用最邻近点迭代（Iterative Closet Point，ICP）方法[11]进行坐标匹配，在完成坐标匹配之后，使用式（1）进行总体偏差的计算：

其中：σ为总体偏差，n为模型中性面上节点的数量，Di为第i个节点距离目标形状的最小距离。

2.5 反变形迭代修正

由于回弹的原因造成变形结果与目标形状的不一致，使用反变形法进行节点位移场的修正，具体方法是利用回弹后变形结果与目标形状之间的差别预估反变形量，将反变形量施加到节点位移场上，以此与回弹量相抵消，减小回弹后形状与目标形状之间的差别。

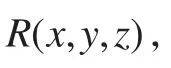
根据式（1）计算得到总体偏差为σi，若σi大于最大允许偏差σmax，则需要进行下一步迭代，则在第（i+1）次迭代中，反变形形状为：

其中k为修正系数，其目的是保证每一次迭代的收敛性，利用反变形对节点位移场进行修正，修正后的节点位移场为：

利用以上迭代算法对图3所示的鞍形目标形状进行计算，设置最大允许偏差σmax=2×10–4，利用程序进行迭代计算，迭代4次后满足精度要求，每次迭代所得到的总体偏差如表1所示。

表 1 迭代次数及总体偏差大小Tab. 1 The number of iterations and the total deviation

将每次迭代计算所得到的形状与目标形状进行对比，以图2中纵向中心线Line1和横向中心线Line2的变形结果进行表示，如图8所示，可以看出随着迭代次数的增加，成型所得到的形状逐渐逼近目标形状，在通过4次迭代计算之后，所得到的形状与所需形状之间的差别已经很小，可以满足精度要求。完成4次迭代后得到的塑性应变分布如图9所示。

3 计算结果验证

根据应变与变形之间的关系，若已知应变分布，就可以计算出该应变分布所对应的变形形状，初应变方法是将应变分布输入到模型上计算该应变分布所对应变形的方法，其可以通过简单弹性有限元计算得到结构的应力和变形，利用这一方法，可以将迭代计算得到的塑性应变以初应变的形式输入到平板模型上，进行弹性计算得到该应变所对应的形状，通过将得到的形状与所需形状进行对比，进行精度的验证。

将图9中塑性应变分布输入到平板模型上，进行弹性有限元计算，得到的形状与所需形状对比如图10（a）所示，两者挠度之差如图10（b）所示，在图10（a）中由于两形状区别非常小，所以得到的2个三维图已经重合，从图（b）中可以看出可以两形状的最大偏差仅0.6 mm，说明经过4次迭代计算得到的应变分布所对应的形状与所需的形状一致，因此可以证明本文介绍的应变分布的计算方法精确。

4 结 语

本文利用弹塑性有限元方法计算成型双向曲率目标形状板所需的应变分布，并利用迭代法对结果进行修正从而提高计算精度，通过本文研究得出以下结论：

1）以节点位移的形式可以将目标形状作为位移载荷输入到有限元模型中，进行弹塑性计算可以得到应变和变形结果；

2）使用反变形迭代修正法可以减少回弹对变形的影响，提高应变分布的精度，随着迭代次数的增加，回弹后的形状逐步逼近于所需的形状，计算得到的应变场精度也随之提高；

3）通过初应变方法对计算得到的应变分布进行弹性计算可以得到应变分布对应的变形，结果表明本文介绍的方法可以精确地计算得到所需形状的应变场，为后续加工路径和工艺参数的确定提供了基础。

[ 1 ]JIN C, Y L YAO. Process design of laser forming for threedimensional thin plates [J]. Transactions of the ASME. Journal of Manufacturing Science and Engineering, 2004. 126(2):217–25.

[ 2 ]XU Zhao-kang. Discuss on forming method for complex curved plate and its applicability [J]. Journal of Wuhan Institute of Shipbuilding Technology, 2006(03): 9–12.

[ 3 ]UEDA Y. Development of computer-aided process planning system for plate bending by line heating (report 1): relation between the final form of plate and the inherent strain(machanics, strength & structural design) [J].Transactions of JWRI, 1991. 20(2): 275–285.

[ 4 ]UEDA Y. Development of computer-aided process planning system for plate bending by line heating (report 2): practice for plate bending in shipyard viewed from aspect of inherent strain[J]. Journal of Ship Production, 1994. 10(4): 239–239.

[ 5 ]UEDA Y. Development of computer-aided process planning system for plate bending by line heating (report 3): relation between heating condition and deformation [J]. Journal of Ship Production, 1994. 10(4): 248–248.

[ 6 ]LETCHER J S. Lofting and fabrication of compound-curved plates [J]. Journal of Ship Research, 1993. 37(2): 166–175.

[ 7 ]SHIN J G, C H RYU. Nonlinear kinematic analysis of the deformation of plates for ship hull fabrication [J]. Journal of Ship Research, 2000. 44(3): 270–277.

[ 8 ]YU G, N M PATRIKALAKIS, T MAEKAWA. Optimal development of doubly curved surfaces [J]. Computer Aided Geometric Design, 2000. 17(6): 545–577.

[ 9 ]ZHANG Xue-biao. Research on ship-hull curved plate forming by pure heating [D]. Dalian: Dalian University of Trchnology,2006.

[10]LIU C, Y L YAO. FEM-based process design for laser forming of doubly curved shapes [J]. Journal of Manufacturing Processes, 2005. 7(2): 109–121.

[11]ZHANG Xue-chang, XI Jun-tong, YAN Jun-qi. Study of inspection technologies based on point cloud for complex surfaces and its system development [D]. Shanghai: Computer Integrated Manufacturing System, 2005(5): 770–774, 780.

Calculating strain field to forming a double-curved shape based on mechanic theory

HU Chang-cheng, ZHAO Yao, YUAN Hua
(School of Naval Architecture and Ocean Engineering Huazhong University of Science and Technology, Wuhan 430074, China)

The determination of process paths and parameters according to the strain field that required to forming a double-curved desired shape is an important work during the process design of line-heating and rolling forming in the process design of line heating and rolling forming. Therefore, the precision of Calculated strain field will affect the accuracy of process paths and parameters. This paper presents a method to calculate the strain filed required to develop a desired shape to a planar shape depend on mechanic theory. Firstly, nodal displacements is applied to the flat plate via elastic-plastic finite element analysis. Owing to the spring back, the shape calculated by elastic-plastic finite element analysis is different between the required shape, then the deviation between calculated shape and required shape is calculated, and reverse deformation is added to nodal displacements, this process continues until the deviation can meet the requirement of precision to terminate the loop. Finally, the obtained strain field is applied to flat model as initial strain to verify the accuracy of this method, and results shows that it has very high calculation precision, this method provide the foundation of the determination of process paths and parameters.

double-curved plate；strain field；mechanics methods；in-plane strain；bending strain

U671.3

A

1672 – 7649(2017)09 – 0006 – 06

10.3404/j.issn.1672 – 7649.2017.09.002

2016 – 11 – 03；

2016 – 12 – 15

胡昌成(1988 – )，男，博士研究生，主要从事板成型和非线性有限元方法方面的研究工作。