基于发电成本与环境效益的风电最佳接入容量分析
2017-09-28王健,沈超,孙伟
王 健,沈 超,孙 伟
(1.江西省电力公司九江供电分公司,江西九江 332000 ;2.河北省电力公司检修分公司,河北石家庄 050070;3.河北省电力公司保定供电公司,河北保定 071003)
基于发电成本与环境效益的风电最佳接入容量分析
王 健1,沈 超2,孙 伟3
(1.江西省电力公司九江供电分公司,江西九江 332000 ;2.河北省电力公司检修分公司,河北石家庄 050070;3.河北省电力公司保定供电公司,河北保定 071003)
为充分了解风电接入电力系统后对发电成本及环境效益的影响,计算符合系统运行经济性的风电接入容量,建立了风电最佳接入容量优化模型。采用该模型分析了不同容量火电机组在不同功率下的煤耗特性变化,并通过对火电机组深度调峰补偿调动火电机组调峰积极性;引入火电排污成本以充分体现风电接入后的环境效益,加入弃风惩罚费用来保障风电优先调度。采用粒子群算法并结合主动搜索技术(active explore basic particle swarm optimization, AEPSO)对模型进行求解,有效解决了粒子群算法易陷入局部最优的问题。最后以某地区实际电力系统为例,计算得出了在最经济运行模式下的风电接入容量,验证了模型的合理性。该研究可为相关决策部门制定风电发展规划提供参考。
风能;发电成本;环境效益;粒子群算法;主动搜索技术;最佳接入容量
近年来,风力发电因其技术成熟、成本低廉、开发潜力巨大及无污染等优点在世界各国都得到了快速发展[1]。风电并网不仅有效降低了系统运行成本[2],还会带来显著的环境效益[3-4]。然而由于风电出力具有的随机性、间歇性及反调峰性等特点[5],随着风电渗透率的不断提高,大规模风电接入电网要求现有运行中的火电机组大幅参加系统调峰,这一方面将为系统安全运行埋下隐患[6-7],另一方面也会造成系统运行成本的上升;当风电并入容量增加到一定程度时,系统为接纳风电增加的成本甚至有可能抵消掉风电接入带来的环境效益。基于此,有必要探索系统在安全运行约束下最经济运行时的风电接入容量。
现有的大多数文献都是在系统调峰容量及线路传输功率约束下,通过优化开机方式和常规机组出力探索以消纳风电最大的系统优化调度方案[8-10],但往往忽视了风电接入电网潜在的环境效益及为接纳风电支出的常规机组的调峰成本。本文从发电成本与环境效益两个角度建立了含风电场的电力系统运行模型,揭示了在不同风电接入容量下火电发电量、污染物排放量及系统调峰成本变化,进而得到了以实现系统综合发电成本最低为目标的风电最佳接入容量。
1 风电最佳接入容量优化模型分析
1.1模型建立
含风电场的电力系统运行特性分析是指在满足系统各种约束条件下,充分发挥风电的低碳环保效益,合理优化火电与风电出力,使得在调度周期内系统总发电成本最小。为更全面的反映接入风电后系统效益变化,在模型中引入火电排污费、火电深度调峰补偿成本及调峰不足导致弃风后的惩罚费用。
1)煤耗量
对于同一火电机组,火电煤耗随着机组出力降低而升高,所以额定工况下为火电机组最经济的运行方式。火电机组的煤耗特性可用式(1)表示:
(1)
式中:Pi为有功输出;ai,bi,ci为机组i煤耗特性参数。
2)火电排污环境成本
燃煤火电消耗的主要是煤炭和水,产生的污染物主要包括SO2,NOx,CO及烟尘等大气污染物。根据中国现行的环保政策,火电厂要为其造成的环境污染付费,收费标准按照《排污费征收使用管理条例》的规定由式(2)决定:
(2)
式中:Ce为火电机组排污成本;μ为每当量污染物收取的费用;Gi为第i种污染物的排放量,kg;Ni为第i种污染物当量值,kg。
火电厂排放污染物当量值如表1所示。

表1 电厂排放各污染物的当量值
文献[11]给出了计算燃煤火电各污染物排放量的常规方法,通过详细的公式可比较准确地计算各污染物排放量。本文采用文献[12]中的污染物排放量的简化计算方法,各污染物排放量可看作只和煤耗与污染物排放率2个参数有关,如式(3)所示:
Ex=η×Sx,
(3)
式中:Ex为火电机组污染物x单位电量的排放量,η为煤耗率;Sx为污染物x单位电量的排放率。
各污染物排放率按表2确定。

表2 污染物排放率
3)火电深度调峰补偿成本
随着风电装机比例不断增大,电网对系统调峰能力的需求越来越高,能否充分发挥火电机组的调峰能力将对风电的消纳量产生直接影响。所以,完善电力系统火电调峰补偿机制将有助于提高火电机组调峰积极性,保障风电消纳。
根据文献[13]对不同容量的火电机组,划分其有偿和无偿调峰界限。如表3所示,调峰补偿标准以β=500元/(MW·h)计。
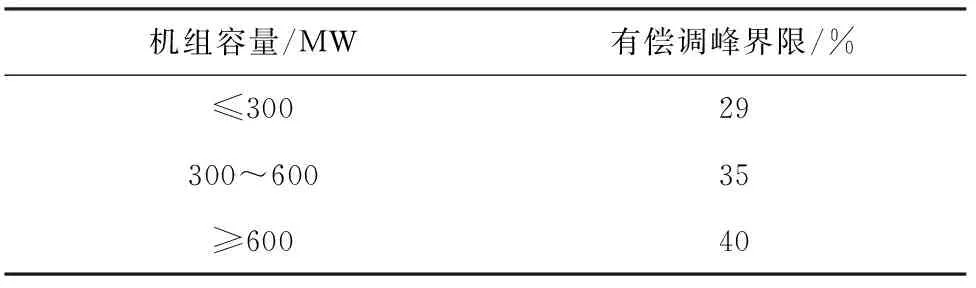
表3 有偿调峰界限的确定
4)弃风惩罚费用
系统发生弃风时,会影响电力系统的节能、环保效益和电量效益,为体现系统接纳风电的优先级,出现弃风时在系统综合成本中加入一定的弃风惩罚费用。弃风惩罚标准根据中国火电上网电价及售电价格的平均值,取0.4元/(kW·h)[14]。
1.2模型目标函数
含风电的系统成本模型目标函数可表示如式(4)所示:
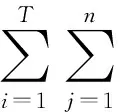
(4)
式中:fcoal(j,i)为机组j在i时段内的耗煤量,t/h;α为煤炭成本;fpeak(j,i)表示机组j在t时段的深度调峰电量;β为火电机组深度调峰时单位发电量补偿费用;fenv为机组j在i时段内的环境成本;fpena(i)为在i时段内的弃风电量;θ为弃风惩罚标准。
1.3模型约束条件
电力系统的安全稳定运行需满足一系列的约束条件,主要包括系统功率平衡约束,系统备用容量约束及各机组出力约束。
1)系统功率平衡约束
(5)
式中:pi_fire,pwind分别为火电机组i和风电场的出力值;pload为负荷值。
2)系统备用容量约束
由于风电出力的不确定性,当把风电加入到系统功率平衡中以后,必然会加大对系统备用容量的需求,系统备用容量如式(6)所示:
S≥pmax_load×(l%+s%)+pr,
(6)
式中:S为系统需要的备用容量;pmax_load为系统最大负荷;l%为负荷备用比例;s%为事故备用比例;pr为检修备用容量。
3)机组出力约束
pm,minμm≤pm≤pm,maxμm,
(7)
式中:pm,min,pm,max分别为机组m的最小与最大出力;μm为机组m的开停机状态量;μm=1表示该机处于运行状态;μm=0表示停机状态。
4)火电机组爬坡约束
Δpimax,down≤pi,t-pi,t-1≤Δpimin,up,
(8)
式中:Δpimax,down和Δpimin,up分别为火电机组i最大下调、上调爬坡率。
2 模型求解算法
基本粒子群算法具有迭代格式简单、可快速收敛及鲁棒性强等特点,但同时也具有易陷入局部最优的缺陷,为使算法能在迭代过程中及时跳出局部最优,本文在基本粒子群算法中加入了主动性搜索技术[15],从而提出一种带主动意识的学习模式,并基于新的学习模式设计了一种改进粒子群算法。
2.1粒子群算法
粒子群优化算法是一种群智能算法,迭代通过逐次迭代粒子将跟踪2个值,一个是粒子本身最优解pbest,称为个体极值,另一个是整个种群最优解Gbest,称为全局极值,并依据公式(9)和公式(10)来不断更新。粒子的速度、位置表示和迭代表达式如下:
(9)
(10)
式中:Vi=[vi1,vi2,…,vin]和Xi=[xi1,xi2,…,xin]分别表示粒子速度和位置;w为惯性权重,用于控制粒子沿原有轨迹运动的程度;c1和c2为学习因子;r1和r2为0到1之间的随机数。
2.2主动性搜索技术
引入主动性搜索的目的是为了增强PSO的全局和局部搜索能力,这样才能有助于PSO跳出局部最优。具体说来,必须赋予粒子适当的主动性来改善种群的全局广度搜索与局部深度搜索能力。为此,采取如下实现技术:
1)在迭代过程中,利用Logistic混沌序列的遍历性,在D维空间搜索区域X上生成T+100个随机遍历位置,为主动探测提供参考点。
设l(d)为D维搜索空间区域X第d维的长度,d=1,2,…,D,t为迭代时间,rand为[0,1]区间上的均匀分布随机函数,定义资源系数与参考点序列如下:
① 资源系数a(d)=3.9+0.1*rand;
② 参考点序列x(t,d)=l(d)*c(t+100,d);
其中c(t,d)为 Logistic 混沌序列,即
c(1,d)=rand;
(11)
c(t+1,d)=a(d)*c(t,d)(1-c(t,d)),t=1,2,…,T+100。
(12)
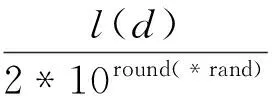
定义t时刻的随机动态邻域ε(x(t),r)为
ε(x(t),r)={p|p(d)∈[x(t,d)-r(d),x(t,d)+r(d)],d=1,2,…,D}。
(13)
3)设m为种群大小,对小邻域ε(x(t),r)进行随机采样,选出m/10或m/102个点与“首领”粒子进行比较并更新。
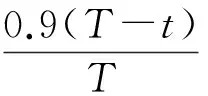
3 算例分析
本文基于中国西北某地区典型日实际负荷特性及该地区风电场的实际出力数据,采用本文建立的风电最佳接入容量优化模型,并应用带主动性搜索的粒子群算法求解模型,分析在接入不同容量风电后系统运行成本和环境效益变化。系统火电机组运行参数及煤耗特性参数[16-17]如表4所示。此时,系统综合调峰深度为λ=31.89%,煤炭价格取α=400元/t。该典型日内负荷率及风电归一化出力值如表5所示,系统最大负荷为4 747 MW。
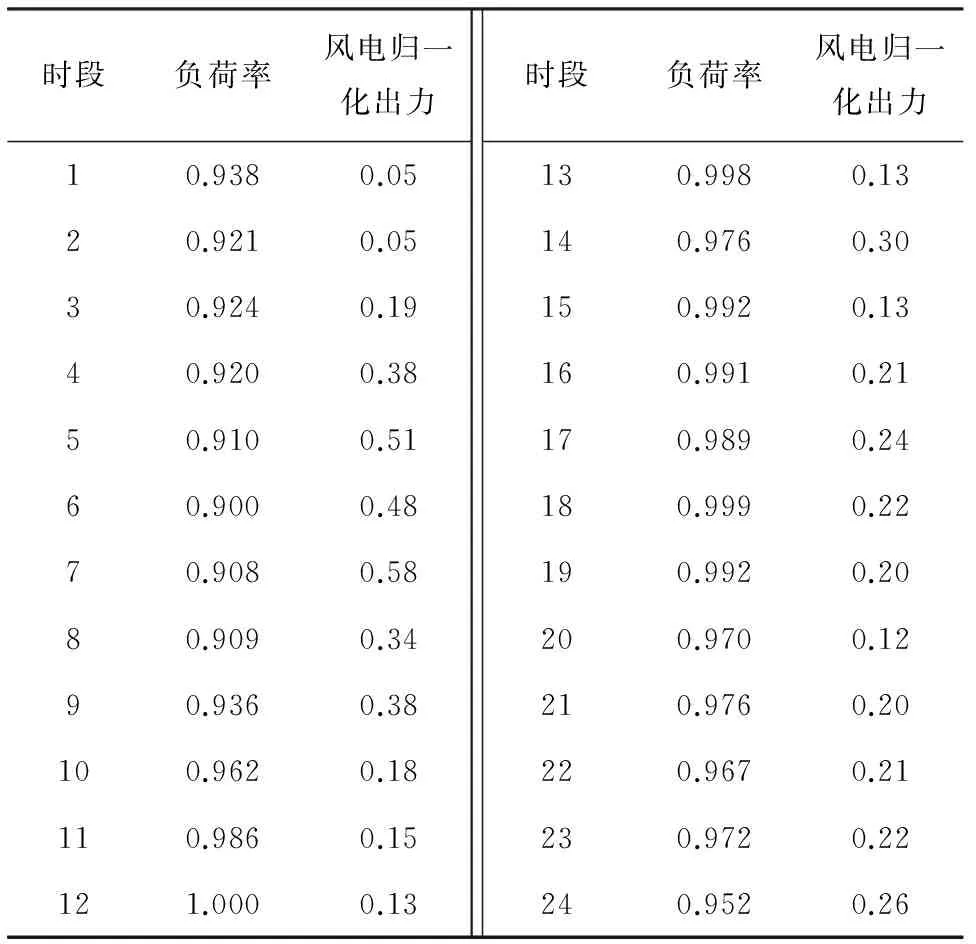
表4 负荷率与风电归一化出力

表5 火电机组运行参数
采用本文的算法对模型求解,得出在不同风电渗透率下系统综合成本变化如图1所示。由图1可知,曲线的最低点处的坐标分别对应系统最佳风电接入容量(1 100 MW)及系统最低综合发电成本(1 309.9万元),系统其他运行结果变化如表6所示。
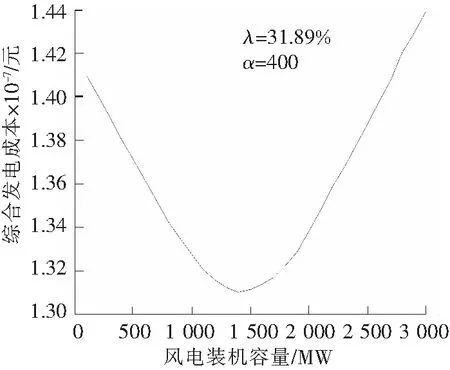
图1 不同风电并网容量下系统综合成本变化Fig.1 Comprehensive cost of electric power system at different wind power capacity

风电装机容量/MW弃风比例/%污染物排放当量/t火电发电量/(亿kW·h)综合成本/万元0014541.07151409.311000.2513540.99191320.0140011.5713280.97141309.9200018.3712890.93961337.9250022.9012620.91771386.9
由表6可知,随着风电装机容量的不断提高,火电发电量逐渐降低,风电的电力效益逐渐显现,替代火电承担了更多的系统负荷;污染物排放量也随着风电并网容量的升高而逐步减少,这体现了风电并入电网后的环境效益;而系统综合成本却随风电容量的增加呈现先减少后增加的趋势。
这说明,在一定程度上,风电容量的增加有助于降低系统的总发电成本,这体现了风电的经济性,但当风电增加到一定比例时,对风电损失的惩罚费用及为接纳风电付出的火电深度调峰补偿成本将超过风电带来的环境与节能效益。
风电装机容量为1 400 MW时,系统综合发电成本降到最低,相对于无风电并入时,污染物排放当量减少了126 t,火电发电量减少了0.100 1(亿kW·h),系统综合发电成本降低了99.4万元,风电的节能减排效益得到很好体现。
风电装机容量为1 100 MW时,弃风比例为0.25%,故1 100 MW可近似看作该地区发生弃风的临界风电装机容量值,而此时综合发电成本为1 320.0万元;风电装机容量为1 400 MW时,系统将会出现11.57%的弃风,但系统综合发电成本降至最低为1 309.9万元,比发生弃风时的临界装机容量值时减少10.1万元。由此可知,在以全额消纳风电的前提下评估得出的最大风电装机容量下,系统综合发电成本未必是最低的。
图2表示了在不同调峰深度下的系统综合发电成本变化。随着调峰深度的升高,曲线的最低点相应的向右下方迁移,即系统最佳风电接入容量逐渐提高,同时在最佳风电接入容量下的系统最低发电成本也逐渐降低。
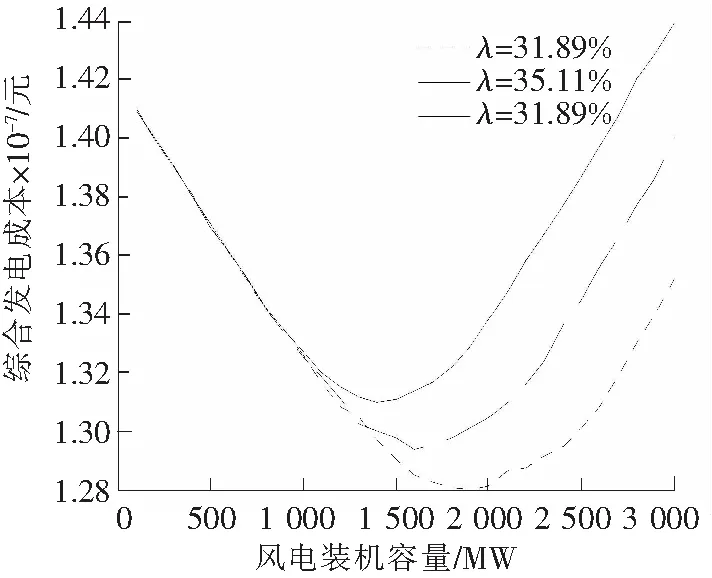
图2 不同调峰深度下的系统综合发电成本Fig.2 Comprehensive cost of electric power system at different peak regulating depth
图3表示了在不同煤炭价格下的综合发电成本变化。由图3可知,风电最佳接入容量并不因煤炭价格的改变而变化,只有系统综合发电成本随着煤炭价格的升高而增加。
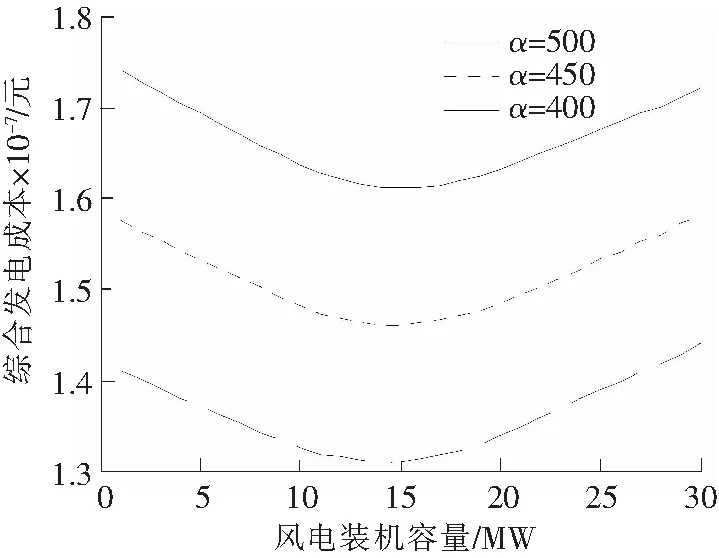
图3 不同煤炭价格下的系统综合发电成本变化Fig.3 Comprehensive cost of electric power system at different price of coal
图4表示了风电出力系数分别为1,0.9和0.8时,在风电不同装机容量下系统综合发电成本的变化,随着风电出力系数的降低,曲线变化呈现整体向右偏移的趋势,即风电最佳接入容量逐渐提高,而系统最低综合发电成本并未因风电出力系数的不同而改变。
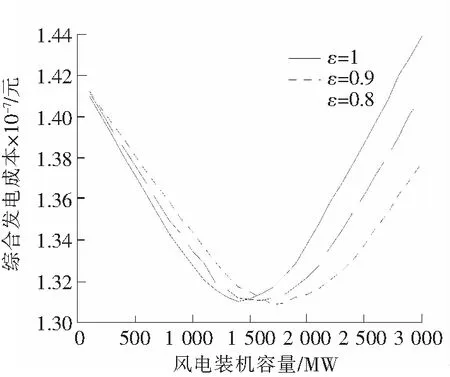
图4 不同风电出力系数下系统综合发电成本Fig.4 Comprehensive cost of electric power system at different wind power coefficient
4 结 语
本文建立了基于发电成本与环境效益的风电最佳接入容量优化模型,通过对模型求解及对结果的分析基本可以得到以下结论。
1)风电并网可带来显著的环境效益且有助于降低系统总体发电成本,但风电装机容量过大反而会造成系统总体发电成本的反弹,在风电为1 400 MW时的并网容量下系统综合成本最低。
2)从系统综合发电成本的角度,以全额消纳风电为前提评估得出的最大风电接入容量与以达到系统综合发电成本最低得出的风电最佳接入容量并不一致,在最佳风电接入容量下,系统会出现一定比例的弃风。
3)提高系统综合调峰深度可提高风电最佳接入容量,同时有助于降低在最佳接入容量下的系统综合发电成本;而煤炭价格的变化对系统最佳接入容量基本无影响,只是改变了系统最低发电成本;不同风电出力系数,对应不同的系统最佳风电接入容量,但系统最低综合发电成本几乎不变。
本文方法可为相关决策部门制定风电发展规划提供参考。因不同地区的电源结构及风资源条件有较大差异,故按本文模型计算得出的不同地区风电最佳接入容量会有所不同。
/
:
[1] 侯婷婷,娄素华,吴耀武,等. 含大型风电场的电力系统调峰运行特性分析[J]. 电工技术学报,2013,28(5):105-111. HOU Tingting, LOU Suhua, WU Yaowu,et al.Analysis on peak load regulation operation characteristics of power system integrated with large-scale wind power[J]. Transactions of China Electrotechnical Society,2013,28(5):105-111.
[2] 刘文颖,文晶,谢昶,等. 考虑风电消纳的电力系统源荷协调多目标优化方法[J].中国电机工程学报,2015,35(5):1079-1088. LIU Wenying, WEN Jing, XIE Chang,et al. Multi-objective optimal method considering wind power accommodation based on source-load coordination[J].Proceedings of the CSEE,2015,35(5):1079-1088.
[3] 陈道君,龚庆武,张茂林,等. 考虑能源环境效益的含风电场多目标优化调度[J].中国电机工程学报,2011,31(13):10-17. CHEN Daojun, GONG Qingwu, ZHANG Maolin,et al. Multi-objective optimal dispatch in wind power integrated system incorporating energy- environmental efficiency[J]. Proceedings of the CSEE, 2011,31(13):10-17.
[4] 王艺博,蔡国伟,郑存龙,等. 考虑合理弃风的风电消纳方法研究[J]. 电测与仪表,2016,53(11):45-50. WANG Yibo, CAI Guowei, ZHENG Cunlong,et al.Study on the accommodation approach of wind power based on rational wind power casting[J].Electrical Measurement & Instrumentation,2016,53(11): 45-50.
[5] 刘畅,吴浩,高长征,等.风电消纳能力分析方法的研究[J].电力系统保护与控制, 2014,42(4): 61-66. LIU Chang, WU Hao, GAO Changzheng, et al.Study on analysis method of accommodated capacity for wind power[J]. Power System Protection and Control, 2014,42(4): 61-66.
[6] 魏博,罗智文,马小晶,等.太阳能吸收装置超调跟踪系统效能分析[J].河北科技大学学报,2013,34(4),377-380. WEI Bo, LUO Zhiwen, MA Xiaojing, et al. Efficiency analysis of overshoot tracking system on solar energy absorb device[J].Journal of Hebei University of Science and Technology,2013,34(4): 377-380.
[7] 李志刚,吴文传,张伯明. 消纳大规模风电的鲁棒区间经济调度(一)调度模式与数学模型[J]. 电力系统自动化,2014,38(20):33-39. LI Zhigang, WU Wenchuan, ZHANG Boming. A robust interval economic dispatch method accommodating large-scale wind power generation part one dispatch scheme and mathematical model[J]. Automation of Electric Power Systems,2014,38(20):33-39.
[8] 杨柳青,林舜江,刘明波,等. 考虑风电接入的大型电力系统多目标动态优化调度[J]. 电工技术学报,2014,29(10): 286-295. YANG Liuqing, LIN Shunjiang LIU Mingbo,et al.Multi-objective dynamic optimal dispatch for large-scale power systems considering wind power penetration[J]. Transactions of China Electrotechnical Society,2014,29(10):286-295.
[9] 董永平,何世恩,刘峻,等.低碳电力视角下的风电消纳问题[J].电力系统保护与控制,2014,42(5):12-16. DONG Yongping, HE Shien, LIU Jun,et al.Wind power consumption problem in the view of low carbon power[J]. Power System Protection and Control,2014,42(5): 12-16.
[10] 胡云岩,张瑞英,王军.中国太阳能光伏发电的发展现状及前景[J].河北科技大学学报,2014,35(1):69-72. HU Yunyan, ZHANG Ruiying, WANG Jun.Development status and prospect of solar photovoltaic power generation in China[J].Journal of Hebei University of Science and Techno-logy,2014,35(1): 69-72.
[11] 黄莹灿,李梦,王燕楠,等. 风电节能减排环境经济效益分析[J]. 中国市场,2014(24):135-139. HUANG Yingcan,LI Meng,WANG Yannan, et al. Analysis on environment economic benefit of wind power mission reduction[J].China Market,2014(24):135-139.
[12] 蔡贵珍,王莹,黄家文,等. 风电工程节能减排环境效益计算方法探讨[J]. 人民长江,2010,41(15):23-26. CAI Guizhen, WANG Ying, HUANG Jiawen,et al.Analysis of calculation methods of environmental benefits from energy saving and emission reduction for wind power project[J]. Yangtze River,2010,41(15):23-26.
[13] 赵晓丽,王玫,赵越,等. 基于火电机组容 量差异的调峰辅助服务补偿机制改进模型[J]. 电力系统自动化, 2013,37(4): 57-61. ZHAO Xiaoli, WANG Mei, ZHAO Yue,et al.A model of compensation mechanism on peak-regulating ancillary services based on capacity variance across thermal power units[J]. Automation of Electric Power Systems,2013,37(4): 57-61.
[14] 张滋华. 含大规模风电电力系统中长期优化运行研究[D].武汉:华中科技大学,2013. ZHANG Zihua.Long-term Optimal Operation of Power System with Large-scale Wind Power Generation[D]. Wuhan:Huazhong University of Science & Technology,2013.
[15] 黄平.粒子群算法改进及其在电力系统的应用[D].广州:华南理工大学,2012. HUANG Ping.Improved Particle Swarm Algorithm and its Application in Power System[D].Guangzhou:South China University of Technology,2012.
[16] 李如琦,秦珍. 计及系统可靠性的机组组合优化运行[J]. 现代电力,2012,29(2):44-49. LI Ruqi, QIN Zhen.The optimization operation of unit commitment by considering system reliability[J].Modern Electric Power,2012,29(2): 44-49.
[17] 张俍. 1 000 MW超超临界火电机组运行优化[D].保定:华北电力大学,2014. ZHANG Liang.1 000 MW Ultra Supercritical Thermal Power Unit Operation Optmization[D].Baoding:North China Electric Power University,2014.
Analysis on optimal wind power integration capacity based on power generation cost and environmental benefit
WANG Jian1, SHEN Chao2, SUN Wei3
(1.Jiujiang Power Supply Company of Jiangxi Electric Power Company, Jiujiang, Jiangxi 332000, China; 2.Hebei Electric Power Maintenance Company,Shijiazhuang, Hebei 050070; 3.Baoding Power Supply Company of Hebei Electric Power Company,Baoding, Hebei 071003, China)
Wind power generation can bring significant environmental and economic benefit, while large-scale wind power integration will cause thermal power peak-regulation, which leads to increasing cost of power generation. In view of this contradiction, an optimization method of wind power integration capacity which accords with the economical operation of the system is put forward. A model of best wind power integration capacity which aims at optimal cost is established, including cost of coal consumption, environmental cost of thermal power pollution, the compensation cost of thermal deep peak-regulation and wind power curtailment cost of wind power curtailment. Considering the constraints of stable operation of power system, this paper adopts particle swarm optimization algorithm combined with active explore technology to solve the model. Based on the actual power system in a certain area, it is concluded that the variation of comprehensive peak-regulation depth, coal price and output coefficient of wind power will affect optimal wind power integration capacity. The research may provide reforence for relevant decision-making section in making wind power development plan.
wind power; power generation cost; environmental benefit; PSO; active explore; optimal integration capacity
1008-1534(2017)05-0339-06
2017-05-24;
2017-08-16;责任编辑:李 穆
国网江西省科技攻关项目(5218D014004M)
王 健(1970—),男,江西景德镇人,高级工程师,主要从事电力行业生产、经营管理等方面的研究。
沈 超。E-mail:1033073356@qq.com
TM715
:Adoi: 10.7535/hbgykj.2017yx05006
王 健,沈 超,孙 伟.基于发电成本与环境效益的风电最佳接入容量分析[J].河北工业科技,2017,34(5):339-344. WANG Jian,SHEN Chao,SUN Wei.Analysis on optimal wind power integration capacity based on power generation cost and environmental benefit[J].Hebei Journal of Industrial Science and Technology,2017,34(5):339-344.
