晋中盆地植物多样性的梯度分布规律研究

刘斌，王应刚

(1.山西省社会科学院，山西太原 030006；2.山西大学，山西太原 030006)

晋中盆地植物多样性的梯度分布规律研究

刘斌1，王应刚2

(1.山西省社会科学院，山西太原 030006；2.山西大学，山西太原 030006)

研究区域植物多样性分布规律对于植物生态环境的保护有重要的意义。以晋中盆地为研究对象，通过设置样方，得出了植物多样性沿城区-郊区-农区的分布规律，在晋中盆地内的县(区、市)的任何一个方向上，随着距离县(区、市)驻地的距离增加，植物多样性也相应增高。用一元回归方法为县(区、市)周围多方向建立了一个植物多样性梯度分布数学模型，模型表明随着距离县(区、市)驻地的距离增加，植物多样性也相应地呈现出线性增加。

晋中盆地；植物多样性；梯度；分布规律

植物多样性包括物种多样性、遗传多样性、生态环境多样性。植物多样性分布格局受到环境因素的影响[1]。国内很多学者从不同角度对植物多样性分布的规律进行研究，比如海拔、利用强度梯度、纬向梯度等，从多维角度揭示了不同的干扰对植物多样性梯度分布规律的影响[2-5]。

本研究以晋中盆地为研究对象，包括榆次区、太谷县、祁县、平遥县、介休市、孝义市、汾阳市、文水县、交城县、阳曲县、清徐县和太原市的6个区(即杏花岭区、万柏林区、迎泽区、小店区、晋源区、尖草坪区)。研究从县城(区、市)建成区开始，沿城区—郊区—农区，由近及远，首先设立了生态样带，在此基础上，用样方调查方法，获取量化数据，揭示植物物种多样性的空间梯度分布规律，建立相应的数学模型。

1 样方设置及调查

1.1样方设置

在研究地区晋中盆地内分布的12个县(区、市)中，用随机抽样法，随机抽取出6个市县(区、市)作为调查研究对象——太谷县、太原市、孝义市、榆次区、文水县、平遥县。针对每一个被抽中的县(区、市)，从县(区、市)建成区的边缘开始向东、南、西、北四个方向分别各设立一条长30 km、宽1 km的生态调查样带，沿样带等距离每隔3 km设置1个规格为0.2 km×1 km的调查样地。在被选中的每一个县(区、市)的每一个方向上设置了11个规格为0.2 km×1 km的调查样地，分别位于距离城区0 km、3 km、6 km、9 km、12 km、15 km、18 km、21 km、24 km、27 km、30 km处，编号依次为1#、2#、3#、4#、5#、6#、7#、8#、9#、10#和11#。再将每一个调查样地划分为100个20 m×100 m的样方。然后，从每个调查样地内的100个样方中，随机抽取6个20 m×100 m的样方作为调查对象，即调查样方。

1.2物种调查

在被随机抽中的样方中进行植物调查，分别记录各个样方中的所有乔木、灌木和草本植物种的种名、高度、数量和盖度等，获取定量化数据。

2 数据处理方法

2.1Gleason index丰富度指数

由于晋中盆地内的人类干扰强烈，自然植被已经被严重破坏，只能见到不连续的斑块状零星分布的植物群落，在此情况下，考虑各个物种之间的数量比例关系已经没有意义。因此，本研究选用不涉及各个物种之间的数量比例关系的Gleason index丰富度指数，计算公式为：

D=S/lnA

式中，S为物种数；A为调查面积；D为Gleason index丰富度指数。

2.2一元线性回归

用一元线性回归法来研究植物多样性即因变量与距离城区距离的远近即自变量之间的统计关系，并建立相应的数学模型即一元回归方程：

Y=aX+b

式中，Y为物种数；X为距离城区的距离；a为斜率；b为截距。

3 结果与分析

3.1单方向数据处理与分析

由于所有调查样方的面积是相同的，所以不再计算Gleason index指数值，而直接用植物物种数代替Gleason index指数值。

3.1.1县(区、市)东方向植物多样性分析

3.1.1.1县(区、市)东方向植物多样性梯度分布规律

依据调查数据，为了克服单个县(区、市)东方向上因偶然因素造成的误差，把被选中的6个县(区、市)东方向上的11个调查点上的调查数据分别组成11个数据组，每个数据组包含36个数据，然后求出各个调查点的平均值，如表1所示，用这些平均值来代表晋中盆地内县(区、市)东方向上的11个调查点上的植物多样性。从表1中的平均值可看出，植物多样性的大小梯度顺序依次为1#<2#<3#<4#<5#<6#>7#<8#<9#<10#<11#，除了7#<6#外，分布规律是距离城区越远的点，植物多样性越高。

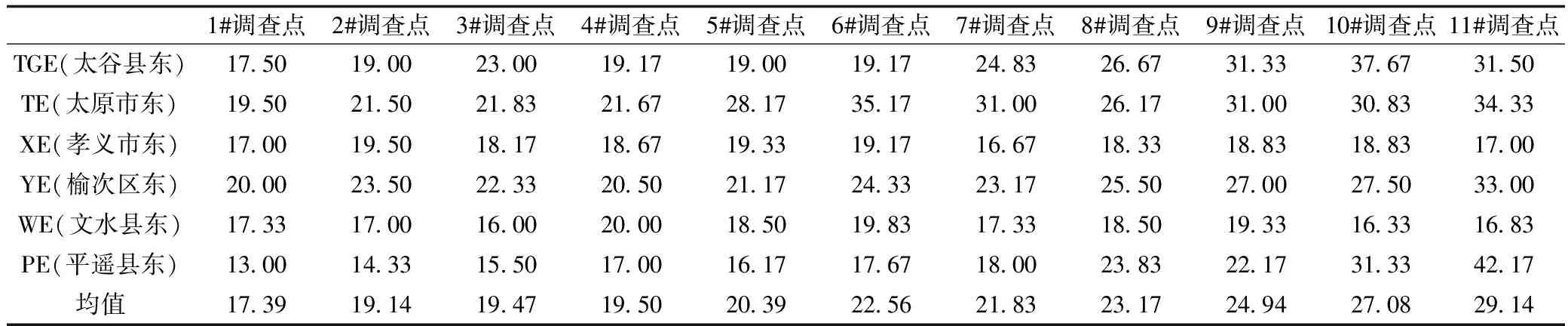
表1 6个县(区、市)东方向上各个点的调查数据

3.1.1.2建立县(区、市)东方向植物多样性梯度分布模型

在各个县(区、市)东方向上设置的11个调查样地上，每一个调查样地上调查6个样方。为了克服单个县(区、市)东方向上单个调查样地上由于自然条件差异和人为干扰程度不同所带来的误差，采取了把6个县(区、市)东方向上位于距离城区相同距离的6个调查样地上的调查样方组成1个样本即数据组，共组成11个样本即数据组，这样在县(区、市)东方向的11个调查样地上各自分别具有36个调查样方，达到了大样本要求。

把县(区、市)东方向的植物物种数量作为因变量，用YE表示；把县(区、市)东方向上距离城区的距离作为自变量，用X表示。用SPSS软件进行一元回归处理，得到如下回归方程即植物多样性梯度分布数学模型和回归系数：

YE=0.3506X+16.978 (R2= 0.9276)

为了更清晰直观地反映在县(区、市)东方向的植物多样性随距离改变而变化的趋势，用表1中的数据作散点图并建立回归直线，如图1所示。从图1看出，总体呈现为距离城区越远，植物多样性就越高。

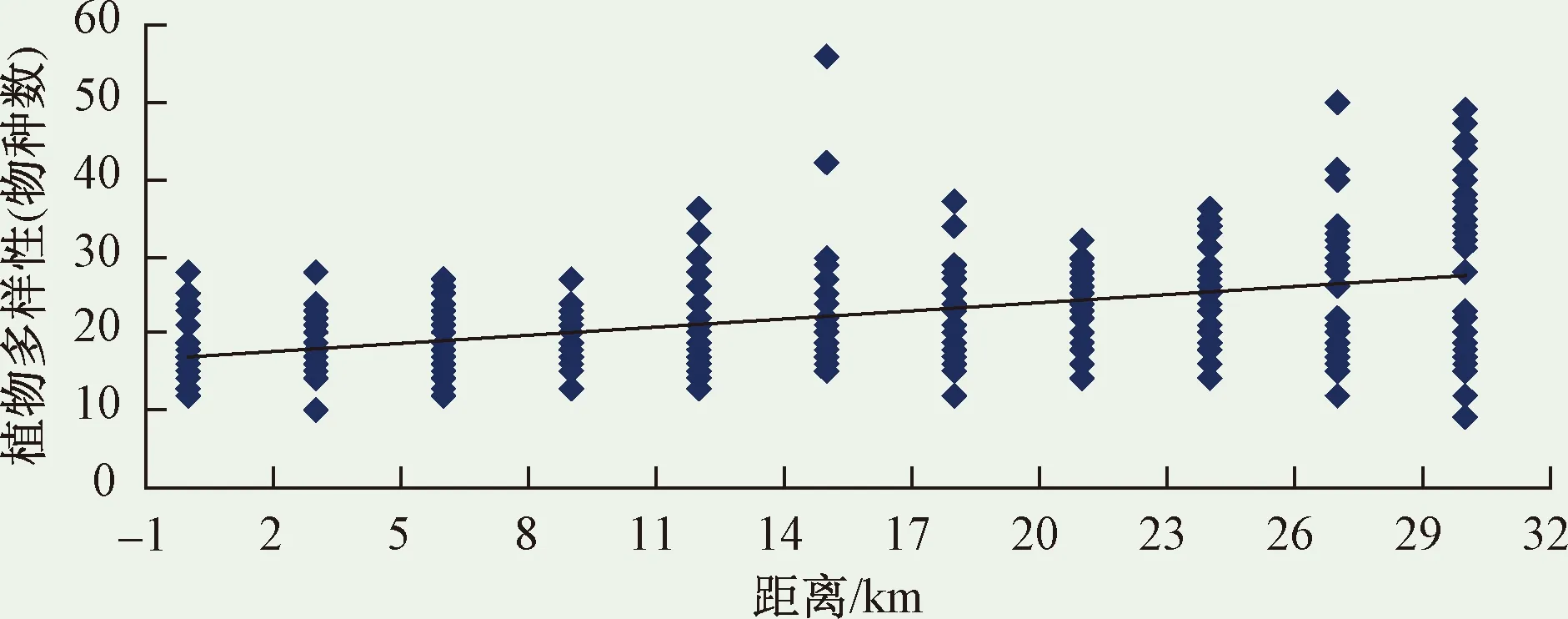
图1 县(区、市)东方向植物多样性变化趋势Fig.1 Gradient change tendency of plant diversity on east direction in county (district or city)

3.1.2县(区、市)南方向植物多样性分析

3.1.2.1县(区、市)南方向植物多样性梯度分布规律

依据调查数据，为了克服单个县(区、市)南方向上因偶然因素造成的误差，把被选中的6个县(区、市)南方向上的11个调查点上的调查数据分别组成11个数据组，每个数据组包含36个数据，然后求出各个调查点的平均值，如表2所示,用这些平均值来代表晋中盆地内县(区、市)南方向上的11个调查点上的植物多样性。从表2中的平均值可以看出，植物多样性的大小梯度顺序依次为1#<2#<3#<4#<5#>6#>7#<8#<9#<10#<11#，除5#>6#>7#外，其余点的分布规律是距离城区越远，植物多样性就越高。

表2 6个县(区、市)的南方向各个点的调查数据

3.1.2.2建立县(区、市)南方向植物多样性梯度分布模型

在各个县(区、市)南方向上设置的11个调查样地上，每1个调查样地上调查6个样方。为了克服单个县(区、市)南方向上单个调查样地上由于自然条件差异和人为干扰程度不同所带来的误差，采取了把6个县(区、市)南方向上位于距离城区相同距离的6个调查样地上的调查样方组成1个样本即数据组，共组成11个样本即数据组，这样在县(区、市)南方向的11个调查样地上各自分别具有36个调查样方，达到了大样本要求。

把县(区、市)南方向的植物物种数量作为因变量，用YS表示；把县(区、市)南方向上距离城区的距离作为自变量，用X表示。用SPSS软件进行一元回归处理，得到如下回归方程即植物多样性梯度分布数学模型和回归系数：

YS=0.2368X+18.761 (R2= 0.7691)

为了更清晰直观地反映在县(区、市)南方向上的植物多样性随距离改变而变化的趋势，用表2中的数据作散点图并建立回归直线，如图2所示。从图2看出，总体呈现为距离城区越远，植物多样性就越高。

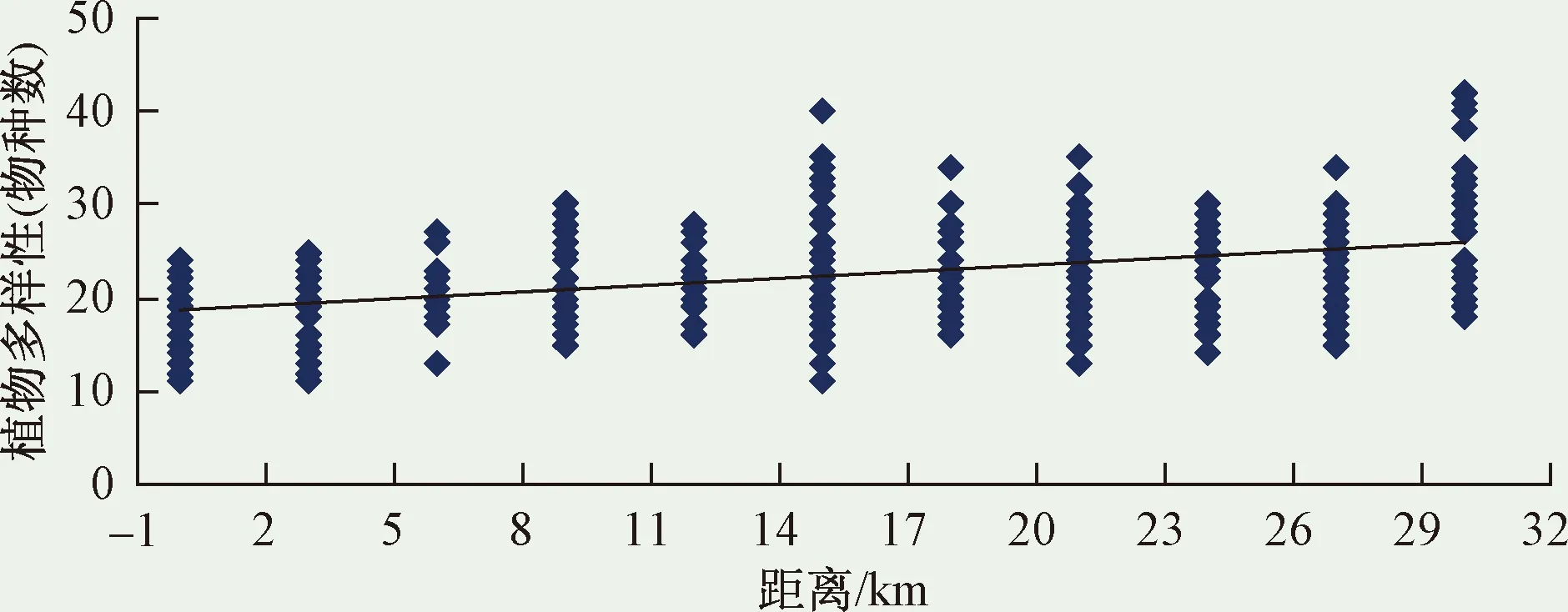
图2 县(区、市)南方向植物多样性变化趋势Fig.2 Gradient change tendency of plant diversity on south direction in county (district or city)

3.1.3县(区、市)西方向植物多样性分析

3.1.3.1县(区、市)西方向植物多样性梯度分布规律

依据调查数据，为了克服单个县(区、市)西方向上因偶然因素造成的误差，把被选中的6个县(区、市)西方向上的11个调查点上的调查数据分别组成11个数据组，每个数据组包含36个数据，然后求出各个调查点的平均值，如表3所示，用这些平均值来代表晋中盆地内县(区、市)西方向上的11个调查点上的植物多样性。由表3可见，植物多样性的大小梯度顺序依次为1#<2#<3#<4#<5#>6#>7#>8#<9#<10#>11#，除5#>6#>7#>8#和10#>11#外，分布规律是离城区越远的点，植物多样性就越高。

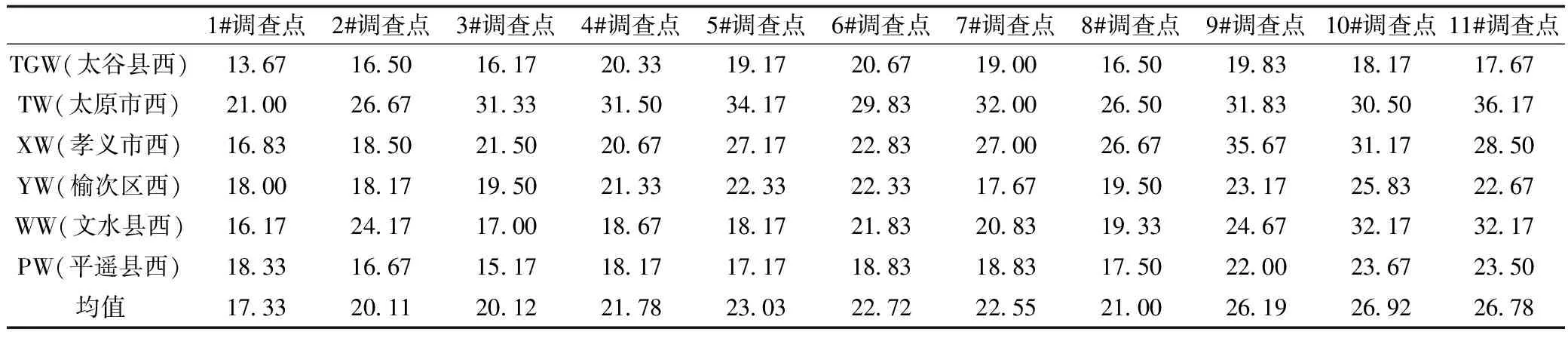
表3 被选中的6个县(区、市)的西方向各个点的调查数据

3.1.3.2建立县(区、市)西方向植物多样性梯度分布模型

在各个县(区、市)西方向上设置的11个调查样地上，每一个调查样地上调查6个样方。为了克服单个县(区、市)西方向上单个调查样地上由于自然条件差异和人为干扰程度不同所带来的误差，采取了把6个县(区、市)西方向上位于距离城区相同距离的6个调查样地上的调查样方组成1个样本即数据组，共组成11个样本即数据组，这样在县(区、市)西方向的11个调查样地上各自分别具有36个调查样方，达到了大样本要求。

把县(区、市)西方向的植物物种数量作为因变量，用YW表示；把县(区、市)西方向上距离城区的距离作为自变量，用X表示。用SPSS软件进行一元回归处理，得到如下回归方程即植物多样性梯度分布数学模型和回归系数：

YW=0.2747X+18.473 (R2= 0.8071)

为了清晰直观地反映在县(区、市)西方向上的植物多样性随距离改变而变化的趋势，用表3中的数据作散点图并建立回归直线，如图3所示。从图3可以看出，县(区、市)西方向总体呈现为距离城区越远，植物多样性就越高。

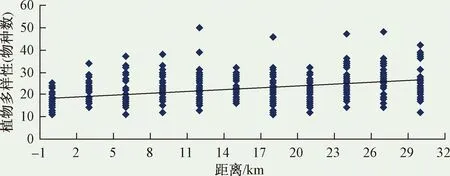
图3 县(区、市)西方向植物多样性梯度分布Fig.3 Gradient distribution of plant diversity on west direction in county (district or city)

3.1.4县(区、市)北方向植物多样性分析

3.1.4.1县(区、市)北方向植物多样性梯度分布规律

依据调查数据，为了克服单个县(区、市)北方向上因偶然因素造成的误差，把被选中的6个县(区、市)北方向上的11个调查点上的调查数据分别组成11个数据组，每个数据组包含36个数据，然后求出各个调查点的平均值，如表4所示，用这些平均值来代表晋中盆地内县(区、市)北方向上的11个调查点上的植物多样性。由表4可见，植物多样性的大小梯度顺序依次为1#<2#<3#<4#>5#<6#<7#>8#<9#<10#<11#，除4#>5#和7#>8#外，总体分布规律是离城区越远，植物多样性就越高。

3.1.4.2建立县(区、市)北方向植物多样性梯度分布数学模型

在各个县(区、市)北方向上设置的11个调查样地上，每一个调查样地上调查6个样方。为了克服单个县(区、市)北方向上单个调查样地上由于自然条件差异和人为干扰程度不同所带来的误差，采取了把6个县(区、市)北方向上位于距离城区相同距离的6个调查样地上的调查样方组成1个样本即数据组，共组成11个样本即数据组，这样在县(区、市)北方向的11个调查样地上各自分别具有36个调查样方，达到了大样本要求。

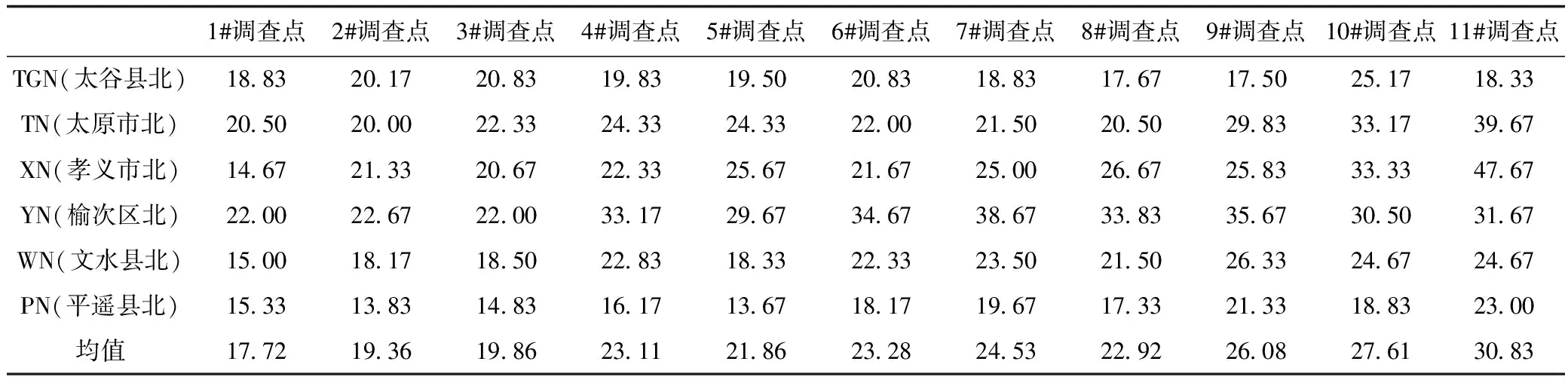
表4 被选中的6个县(区、市)的北方向各个点的调查数据

把县(区、市)北方向的植物物种数量作为因变量，用YN表示；把县(区、市)北方向上距离城区的距离作为自变量，用X表示。用SPSS软件进行一元回归处理，得到如下回归方程即植物多样性梯度分布数学模型和回归系数：

YN=0.3621X+17.946 (R2= 0.8941)

为了直观地反映在县(区、市)北方向上的植物多样性随距离改变而变化的趋势，用表4中的数据作散点图并建立回归直线，如图4所示。从图4可以看出，总体呈现为距离城区越远，植物多样性就越高。

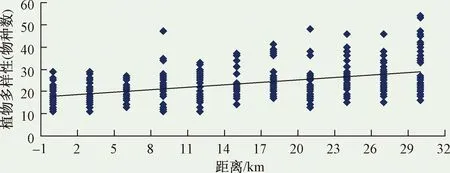
图4 县(区、市)北方向植物多样性梯度分布Fig.4 Gradient distribution of plant diversity on north direction in county (district or city)

3.2县(区、市)周围多方向数据处理与分析

前面分析的是县(区、市)东、南、西、北单方向上的植物多样性梯度分布规律，并建立了单方向植物多样性梯度分布数学模型。现在来分析县(区、市)周围多方向上的植物多样性梯度分布规律，并建立多方向共用的植物多样性梯度分布数学模型。

3.2.1县(区、市)周围多方向植物多样性梯度分布规律

为了克服单个县(区、市)东、南、西、北各个方向上由于自然条件差异和人为干扰程度不同所带来的误差，把6个县(区、市)东、南、西、北各个方向上位于距离城区相同距离的所有调查样方组成1个样本即数据组，共组成11个样本即数据组，每一个样本即数据组含有144个样方即数据。然后求出各个调查点的平均值，如表5所示，用这些平均值来代表晋中盆地内县(区、市)周围多方向上的11个调查点上的植物多样性。

由表5可见，植物多样性的大小梯度顺序依次为1#<2#<3#<4#<5#<6#>7#>8#<9#<10#<11#，除6#>7#>8#外，总体分布规律是距离城区越远，植物多样性就越高。

3.2.2建立县(区、市)周围多方向植物多样性梯度分布数学模型

为了建立适合当地县(区、市)周围各个方向的植物物种多样性梯度分布模型，在6个县(区、市)各自的东、南、西、北方向上分别各设置11个调查点，每1个调查点上随机调查6个样方。为了克服单个县(区、市)东、南、西、北各个方向上由于自然条件差异和人为干扰程度不同所带来的误差，把6个县(区、市)东、南、西、北方向上位于距离城区相同距离的各个点上的调查样方分别组成1个样本，共组成11个样本，这样在每一个等距离调查点上的样本含量为144个样方即数据，达到了超大样本要求。

把县(区、市)周围多方向的植物多样性作为因变量，用YC表示，把县(区、市)周围多方向上距离城区的距离作为自变量，用X表示。用SPSS软件进行一元回归处理，得到如下一元回归方程即植物多样性梯度分布数学模型和回归系数：

YC=0.3062X+18.036 (R2= 0.9128)

为了更清晰直观地反映在县(区、市)周围多方向的植物多样性随距离改变而变化的趋势，用表1至表4中的数据作散点图并建立回归直线，结果如图5所示。从图5可以看出，县(区、市)周围总体呈现为距离城区越远，植物多样性就越高。

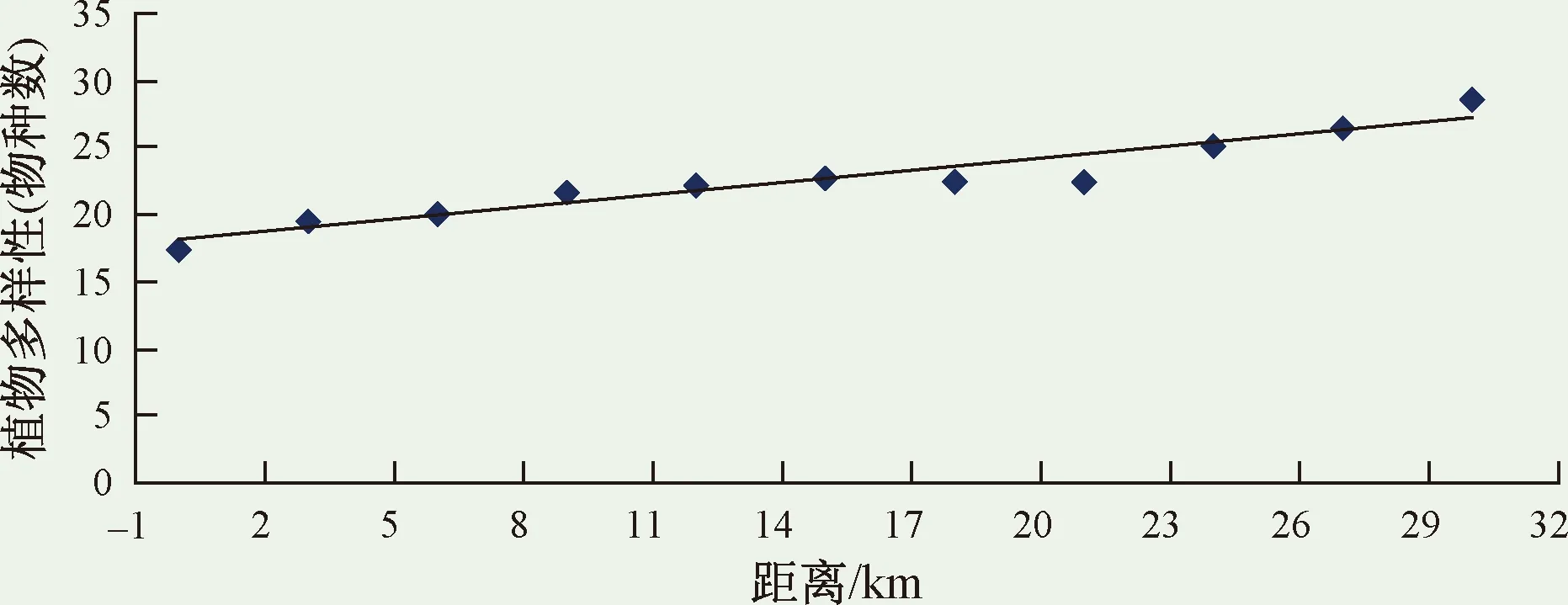
图5 县(区、市)周围多方向植物多样性变化趋势Fig.5 Gradient change tendency of plant diversity on multi-direction around county (district or city)

4 结论

首先，通过对6个县(区、市)的东、南、西、北4个方向分别组成各自的样本数据进行单方向植物多样性分析，结果表明：在东方向上，最靠近城区的1#点的植物多样性最低为17.39，离城区最远的11#点的植物多样性最高为29.14，相邻调查点两两之间的平均梯度差为1.18；在南方向上，最靠近城区的1#点的植物多样性最低为17.53，离城区最远的11#点的植物多样性最高为28.11，相邻调查点两两之间的平均梯度差为1.06；在西方向上，最靠近城区的1#点的植物多样性最低为17.33，离城区最远的11#点的植物多样性最高为26.78，相邻调查点两两之间的平均梯度差为0.95；在北方向上，最靠近城区的1#点的植物多样性最低为17.72，离城区最远的11#点的植物多样性最高为30.83，相邻调查点两两之间的平均梯度差为1.31。由此可见，在晋中盆地内的县(区、市)的东、南、西、北任何一个方向上，随着距离县(区、市)驻地距离的增加，植物多样性也相应增高。

其次，用一元回归方法为县(区、市)东、南、西、北各个方向分别建立了一个植物多样性梯度分布数学模型。从4个数学模型看，各个模型的斜率即a值均大于0.2368，并且截距即b值也都大于16.978。表明随着距离县(区、市)驻地的距离增加，植物多样性也相应地呈现出线性增加趋势。这些模型可分别用于对县(区、市)东、南、西、北各个方向上任何一点的植物多样性进行预测。

最后，对县(区、市)周围多方向植物多样性梯度分布规律进行分析表明，在县(区、市)周围各个方向上，最靠近城区的1#点的植物多样性最低为17.49，离城区最远的11#点的植物多样性最高为28.72，相邻调查点两两之间的平均梯度差为1.12。由此可见，在晋中盆地内的县(区、市)周围的任何一个方向上随着距离县(区、市)驻地的距离越远，植物多样性也相应越高。此外，用一元回归方法为县(区、市)周围多方向建立了一个植物多样性梯度分布数学模型。从该数学模型看，模型的斜率即a值为0.3062，截距即b值为18.036。表明随着距离县(区、市)驻地的距离增加，植物多样性也相应地呈现出线性增加。此模型可用于对县(区、市)周围任何方向上任何一点的植物多样性进行预测。

[1] Chesson P. Mechanism of maintenance of species diversity[J]. Annual Review of Ecology and systematics, 2000, 31: 343- 366.

[2] 金慧, 赵莹, 赵伟, 等. 长白山牛皮杜鹃群落物种多样性的海拔梯度变化及相似性[J]. 生态学报, 2015, 35(1): 125- 133.

[3] 胡云锋, 艳燕. 内蒙古东北-西南草地样带植物多样性变化[J]. 资源科学, 2012, 34(6): 1024- 1031.

[4] 李昊民, 喻庆国, 王娟, 等. 云南生物多样性分布格局的梯度分析[J]. 西部林业科学, 2013, 42(5): 24- 31.

[5] 蔡蕾, 潘远智, 何飞, 等. 高寒草甸花卉生物多样性与生物量海拔梯度特征研究动态[J]. 四川林业科技, 2011, 32(3): 60- 65.

[6] 孙荣, 袁兴中, 刘红, 等. 三峡水库消落带植物群落组成及物种多样性[J]. 生态学杂志, 2011, 30(2): 208- 214.

Study on Gradient Distribution of Plant Diversity in Jinzhong Basin

LIU Bin1, WANG Ying-gang2

(1.Shanxi Academy of Social Sciences, Taiyuan 030006, China; 2.Shanxi University, Taiyuan 030006, China)

The study of regional plant diversity distribution has great significance for the protection of ecological environment. This study selects Jinzhong basin as the research object. By setting the plot, this paper generates the distribution regularity of plant diversity along the urban-suburban-rural areas. The research finds that in any outward direction of counties (district or city) in the Jinzhong basin , as the distance from the county (district or city) center increases, the plant diversity also increases. The paper also establishes a model of plant diversity gradient distribution with regression which shows that as the distance from the county (district or city) center increases, the plant diversity also shows a linear increase.

Jinzhong basin; plant diversity; gradient; distribution pattern

10.14068/j.ceia.2017.05.015

X503.23

： A

： 2095-6444(2017)05-0069-06

2017-07-25

国家自然科学基金(31070424)

刘斌(1985—)，男，山西运城人，助理研究员，硕士，主要研究方向为生态学和社会影响评价，E-mail:543787381@qq.com