空间3-RPC柔顺并联机构拓扑优化设计*

杜海堂,张荣兴

(江西理工大学 机电工程学院，江西 赣州 341000)

空间3-RPC柔顺并联机构拓扑优化设计*

杜海堂,张荣兴

(江西理工大学 机电工程学院，江西 赣州 341000)

为了获得空间柔顺并联机构构型,基于传统并联机构的设计原型，采用拓扑优化理论对空间并联机构进行拓扑优化设计。首先，以空间3-RPC并联机构为研究对象，建立机构的微运动学矢量连续映射Jacobian矩阵。然后，建立空间3-RPC柔顺并联机构的拓扑优化SIMP模型，运用优化准则算法(Optimization Criterion)对所建立的SIMP模型求解。最后，运用曲线拟合方法对拓扑后的构型轮廓进行拟合修正，采用SolidWorks 软件建立其拟合修正后的模型，进而通过HyperWorks有限元软件对机构进行静力学分析。仿真结果表明：与同构型的传统并联机构相比，拓扑优化后的空间柔顺并联机构具有相同的微动特性，因而验证了空间并联机构的拓扑优化设计方法的有效性。

3-RPC柔顺并联机构；微运动矢量映射；拓扑优化设计；静力学仿真

0 引言

精密制造是衡量一个国家制造水平高低的重要标志，目前，精密制造行业已经在航空航天、汽车、微机电系统、医疗等领域得到了广泛应用[1]。随着科技的发展，空间柔顺并联机构的设计也在不断地发展，对其要求也在不断的提高。同时，面临的挑战和机遇也越来越多。从当前国内外发展情况来看，现阶段对自由度并联机构的拓扑优化研究相对而言比较少，而对二维结构的拓扑优化研究相对比较成熟，三维结构主要集中在构件结构的研究上面，仍处于发展阶段[2]。饶柳生等[3]以车床筋板为载体，使用多目标优化加权的设计理念对其进行设计，提高了机床的动态和静态性能，但没有研究车床筋板在多阶固有频率下的特性。陈建超等[4]以载荷路径的遗传算法为基础，为了达到机翼轻量化设计的目标，分别从单一材料和复合材料的角度出发,对机翼前缘进行优化，但是多材料组合形式机翼的运动学和动力学建模非常复杂。刘林华等[5]以越野车车架为载体，采用多目标方法对越野车车架进行研究，但是平均频率法建模只能近似地反映车架的运动性能。与成熟的二维结构拓扑优化相比，三维结构的拓扑优化还处在发展阶段，具有一定的难度和挑战。再加上空间并联机器人因其具有精度高、刚度大、结构稳定等特点，在实际生产中有广阔的应用前景，如：微操作机器人、虚拟轴机床以及用于精密装配的机械手等[6-8]。为了更好地将拓扑优化方法与空间并联机器人相结合，以改善空间并联机器人的运动特性和动态性能。本文主要基于机构的输入输出矢量连续映Jacobian矩阵，并结合拓扑优化方法[9]对空间3-RPC并联机构进行拓扑优化设计，将拓扑优化后的构型与传统并联机构进行静力学分析和对比，仿真结果表明无论是运动状态还是运动精度，空间柔顺并联机构均比传统的空间并联机构更具有优越性，并定量证明了拓扑优化方法的合理性和可行性。

1 机构的矢量连续映射Jacobian矩阵

1.1 3-RPC并联机构模型

3-RPC是对称形式的三自由度并联机构，其结构简图如图1所示。3-RPC并联机构的动定平台以三条支链的形式相连接，其每条支链含有一个转动副R，一个移动副P和一个圆柱副C。R副与定平台相连，C副与动平台相连，P副连接着R副和C副。动定平台由两个等边三角形△abc和△ABC组成。分别在模型的动定平台建立坐标系o-xyz和O-XYZ,o和O分别是动定平台的中心。其中，动定平台的边长分别为m和n，驱动杆的长度为l,支链与定平台的夹角为φi。

图1 3-RPC并联机构结构简图

1.2 矢量连续映射Jacobian矩阵求解

对于多自由的并联机构，可采用螺旋法求解其输入输出的Jacobian矩阵。但是对于少自由度的并联机构，螺旋法得到的矩阵往往不是方阵，且不能避免计算过程中求解超越方程组的问题。应用微运动法求解Jacobian矩阵，无需求解超越方程组，所得到的Jacobian矩阵为非奇异方阵，可以直接作为并联机构仿真系统的理论参考输入值。微运动法的基本思想为：当机构转动的角度α,β,γ或者移动的距离dx,dy,dz较小时，下列等价形式成立：

(1)

式中：δv表示α,β,γ,dx,dy,dz及其高阶量。

假设动平台坐标系的x,y,z轴相对于定平台分别转动了γ,β,α以及平移了dx,dy,dz，根据静坐标系变换原则，可得到相应的旋转变换矩阵Rα,β,γ和平移变换矩阵Ttrans。

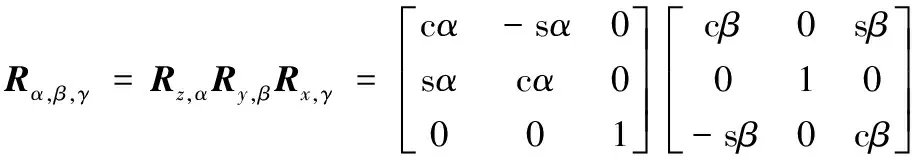
其中，c()=cos(),s()=sin()，下同。

综上，可得到齐次坐标变换矩阵：

定平台各个铰链中心a,b,c在O-XYZ中的坐标向量为：

动平台各个铰链中心A,B,C在o-xyz中的坐标向量为：

根据齐次变换矩阵T，由公式P′=TP可得动平台各个铰链中心a,b,c旋转变换后在O-XYZ中的齐次坐标向量如式(1)所示。由于该并联机构主要实现的是沿x轴，y轴和z轴的平移，所以将机构沿x轴的平移dx，沿y轴的平移dy和沿z轴的平移dz作为机构的输出量。根据dx,dy,dz求解各杆的杆长变化，并将其作为机构的输入量。

将机构的所有参数写入Matlab的m文件中，编写求解杆长变化量和输入输出矢量连续映射关系的Jacobian矩阵程序。通过Matlab计算各杆长的变化量，可得到Δli与dx,dy,dz之间的关系，其齐次坐标形式如式(2)所示。

(2)

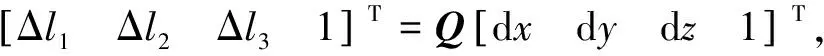
2 空间柔顺并联机构拓扑优化设计

2.1 SIMP优化模型的建立

材料的构成与结构单元属性之间的映射关系主要是由材料的插值模型体现，不同的材料插值模型会产生不同形式的优化结果[10]，从而对最终的拓扑结构产生不同的影响。本文选择SIMP插值模型对全柔性并联机构进行优化。SIMP插值模型如下：

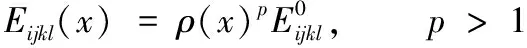
(3)

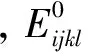
根据螺旋和反螺旋原理可知，三自由度的空间柔顺并联机构存在三个输出量。为了达到承载能力更强的目的，以柔度最小为目标函数、以体积最小为约束条件和以质量作为设计变量进行设计，以SIMP材料插值法为前提提出并建立空间三自由度柔顺并联机构的静态柔度拓扑优化模型：

(4)

式中：c(x)，U，u0，F，K，k0，f，V(x)，V0,N分别代表三维结构的整体柔度、整体位移矩阵、单元位移矩阵、整体力矩阵、整体刚度矩阵、单元初始刚度矩阵、约束体积比、优化后体积、优化前结构初始体积、离散总单元数，xmin和xmax分别代表优化过程中的最小密度和最大密度值。

2.2 优化模型求解

由于空间三自由度柔顺并联机构的静力学拓扑优化问题属于单目标、单约束问题，通过分析比较，可知优化准则法(OC)更适合优化求解，因此本文选择OC算法对设计变量进行更新迭代，公式如下所示：

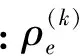
式中：Ve为单元的第k步迭代体积。Λ(k)为体积约束下第i步迭代的Lagrange乘子，其采用双向凸线性规划法的更新准则。

3 拓扑优化模型仿真

对建立的空间3-RPC柔顺并联机构进行拓扑分析。具体参数设置如下: 将设计区域及非设计区域材料均定为钢材，实体部分的弹性模量为205GPa,泊松比为0.3,优化体积比为0.3,最小过滤半径设置为1.5，最小离散网格大小设置为1.5mm，输入力大小为F1=F2=F3=1000N。分别对空间结构进行约束边界条件的设置、力的加载设置、网格划分设置以及优化条件设置，根据设计要求，以柔度最小为设计目标，密度为设计变量，对空间机构的体积进行约束，选取体积约束比为0.3，对3-RPC柔顺并联机构进行优化设计，初始设计分析及设计工况如图2所示。

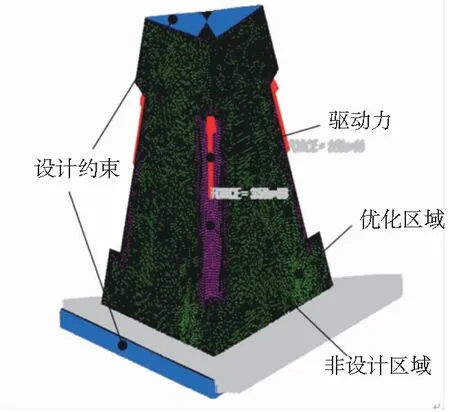
图2 3-RPC型并联机构仿真设计模型

其中：粉色表示非设计区域，即压电陶瓷预留安装区及向其四周扩散的6mm区域，绿色表示设计区域(即优化区域)，红色表示加载的驱动力，蓝色表示所设计的约束，分别对动平台和定平台进行约束并将动平台设置成统一的刚性体。

以所设计的工况为基础，在OptiStruct中对3-RPC并联机构进行拓扑优化设计，得到拓扑优化后的新构型，在Hyperview中对其密度云图进行察看，得到迭代曲线如图3所示，优化后的构型如图4所示。

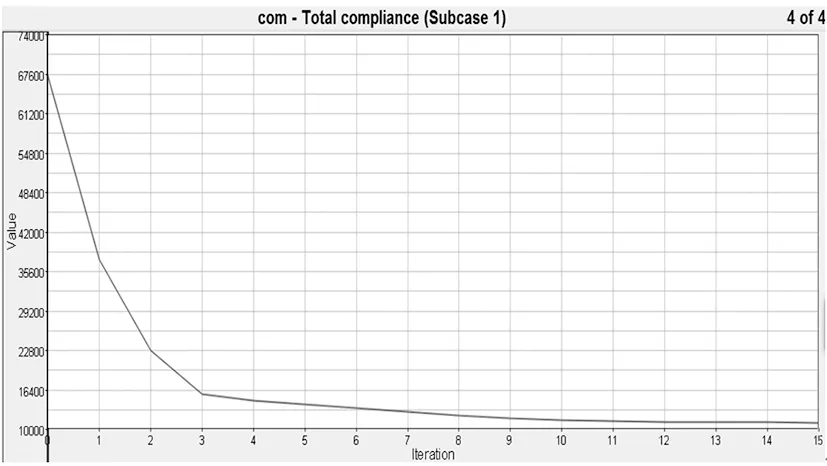
图3 目标函数与迭代次数变化关系图

图4 拓扑优化后的结构密度云图

从图3观察可以得出：随着迭代次数的增加，优化设计的结果逐渐趋于稳定趋势，到第九步的时候已成稳定趋势，基本完成优化构型，到第十五步的时候已经满足迭代精度要求，优化结束。将阀值设定为0.5，在有限元软件中查看优化后的结构，如图5所示。

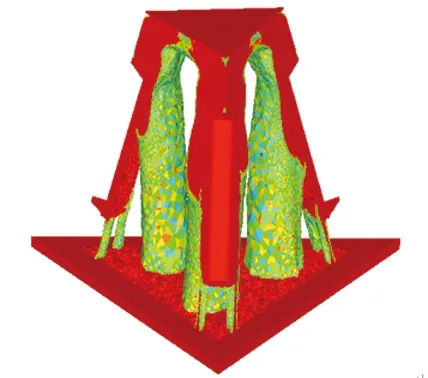
图5 阀值为0.5的拓扑优化结构

从图5观察可以得出：将其优化后的结构作为重新建立三维模型的参考依据， 然后进行轮廓拟合和边界光顺处理并将其在Ossmouth中导出，保存为IGS格式并导入Solidworks软件中，建立空间三自由度柔顺并联机构的三维实体模型，如图6所示。

图6 柔顺并联机构实体模型

4 静力学分析

对拓扑优化后的3-RPC空间柔顺并联机构进行静力学分析。首先，在Solidworks中对其进行三维模型的建立，并以STEP格式保存。其次，将STEP格式的三维模型导入Hyperworks中，分别进行有限元网格划分、材料属性的赋予、控制卡片的选择、边界条件的设置以及力的加载。最后，力的加载设置和约束条件为工况的前提下，在Radioss中对其进行静力学分析。通过Hyperview观察3-RPC空间柔顺并联机构的仿真结果，并将机构的仿真结果和矢量映射关系计算所得出的结果进行对比。机构X,Y,Z三个方向的位移云图如图7～图9所示。

设置动平台和定平台的初始设计条件定为正三角形，边长分别为75mm,75mm,150mm，驱动边与定平台夹角设为φ=75°，输入分别设为dx=5.3×10-3mm,dy=2.4×10-2mm,dz=-3.43mm。通过式(2)可以得出机构在X,Y,Z三个方向上的输出结果分别为Δl1=1.30×10-3mm,Δl2=-8.99×10-2mm,Δl3=9.01×10-2mm，转动均值为0°，理论值与仿真结果对比如表1所示。

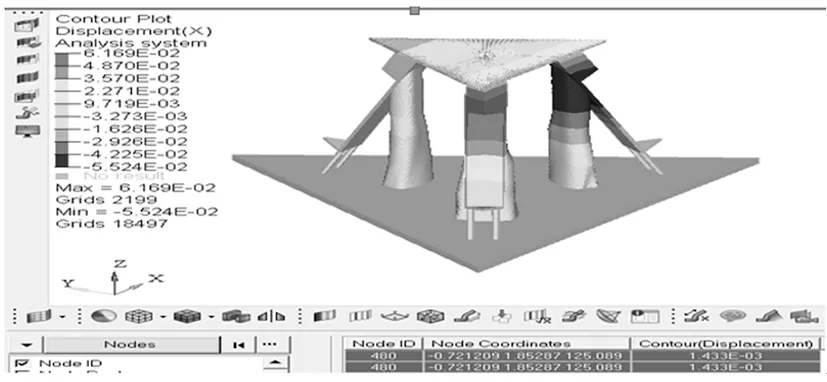
图7 X方向位移云图

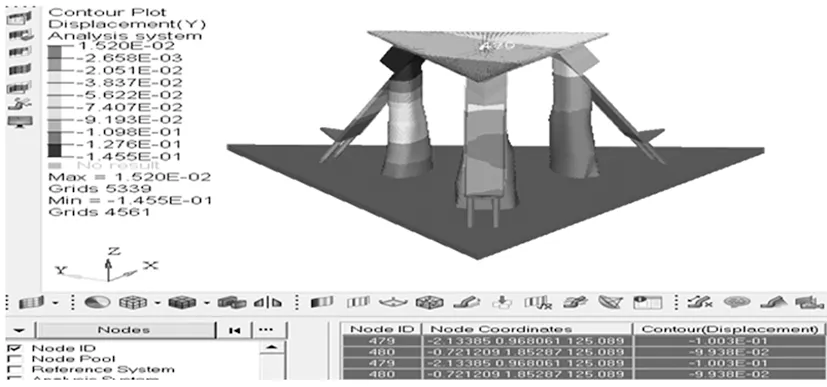
图8 Y方向位移云图

图9 Z方向位移云图

表1 理论值与仿真值对比

从表1对比可知：①拓扑优化设计方法所设计出的新3-RPC柔顺并联机构在X、Y、Z三个方向可以达到微米级的位移精度；②理论计算所得的参数与优化设计仿真所得到的参数在同一个数量级上。因此，以上可验证采用拓扑优化方法设计得到的空间柔顺并联机构是可行有效的。

5 总结

本文分析了3-RPC并联机构输入输出之间的矢量连续映射关系，在此基础上建立了空间柔顺并联机构的SIMP 拓扑优化模型，并运用 OC 算法对所建立的模型进行求解。通过曲线拟合方法对拓扑后的构型轮廓拟合修正并建立其三维实体模型。运用HyperWorks有限元软件对机构进行静力学分析，结论如下：

①在相同载荷输入的条件下，与同构型的传统并联机构相比，拓扑优化后的柔顺并联机构具有相同的运动特性，验证了基于微运动矢量映射Jacobian矩阵拓扑优化设计方法的有效性。②拓扑优化得到的柔顺并联机构具有微动特性，可达到微米级的位移精度。

[1] 雒建斌.机械工程学科发展战略报(2011-2020)[M].北京：科学出版社,2010.

[2] 中国机械工程学会.中国机械工程技术路线图[M].北京：中国科学技术出版社,2011.

[3] 饶柳生,侯亮，潘勇军. 基于拓扑优化的机床立柱筋板改进[J].机械设计与研究，2010，26(1)：87-92.

[4] 陈建超，张永红，葛文杰,等. 基于多材料组合的柔性机翼前缘拓扑优化[J].机械设计,2011,28(6): 61-66.

[5] 刘林华,辛勇，汪伟.基于折衷规划的车架结构多目标拓扑优化设计[J].机械科学与技术，2011,30(3)：382-385.

[6] 于靖军,李守忠,裴旭,等.一种刚柔统一的并联机构构型综合分析[J].中国科学,2011,41(6):760-773.

[7] 田俊,张宪民.基于柔顺机构的两自由度微动平台的分析设计[J].机械设计与制造,2009(5):205-207.

[8] Sigmund O. On the Design of Compliant Mechanisms Using Topology Optimization[J]. Mechanics of Structures & Machines, 2005,25(4): 493-524.

[9] Sigmund O, Torquato S. Design of materials with extreme thermal expansion using a three-phase topology optimization method[J]. Proceedings of SPIE-The International Society for Optical Engineering, 1997, 45(6):1037-1067.

[10] Kee-Bong Choi , Jae Jong Lee ,Gee Hong Kim, et al. A Compliant Parallel Mechanism with Flexure-based Joint Chains for Two Translations[J].International Journal of Precision Engineering and Manufacturing, 2012,13(9):1625-1632.

(编辑李秀敏)

OptimizationDesignfortheSpatial3-RPCCompliantParallelMechanism

DU Hai-tang，ZHANG Rong-xing

(School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou Jiangxi 341000, China)

In order to get the spatial compliant parallel mechanism, based on the design prototype of parallel mechanism topology optimization design was carried out by using topology optimization theory. Firstly, based on the spatial 3-RPC parallel mechanism, the differential continuous vector mapping relationship between the compliant parallel mechanism and the traditional parallel mechanism was established. Secondly, the topology optimization SIMP model of spatial 3-RPC compliant parallel mechanism was established, and the model was solved by using the optimization criterion algorithm. Finally, based on the curve fitting method, the whole configuration profile was fitted and by using SolidWorks software the 3D model was established, and then the static simulation analysis and comparison were presented based on finite element software. The simulation results show that the spatial compliant parallel mechanism after topology optimization and the traditional parallel mechanism have the same movement characteristics, which qualitatively verified the effectiveness of the topology optimization method for the spatial parallel mechanism.

3-RPC compliant parallel mechanism; micro-motion vector mapping; topology optimization design; static simulation

TH112；TG659

：A

1001-2265(2017)09-0031-04

10.13462/j.cnki.mmtamt.2017.09.009

2016-11-24；

：2016-12-14

国家自然科学基金资助项目(51165009, 51105077);中国博士后科学基金资助项目(2013M541874)

杜海堂(1989—)，男，江西赣州人，江西理工大学硕士研究生，研究方向为并联机构构型综合及其智能控制，(E-mail)1477802269@qq.com。