流固耦合作用下的液控换向阀动态特性仿真

张顺锋，张 胜，王 强，何晓晖，徐 磊

(解放军理工大学 野战工程学院， 南京 210007)

【机械制造与检测技术】

流固耦合作用下的液控换向阀动态特性仿真

张顺锋，张 胜，王 强，何晓晖，徐 磊

(解放军理工大学 野战工程学院， 南京 210007)

基于流固耦合理论和动网格技术，运用CFD-ACE+软件建立了计算流体力学三维模型。对在弹簧力、驱动力及流体力的作用下液控换向阀的开启过程进行了仿真，仿真结果与理论值、AMESim数值计算基本一致。对3种节流结构的液控换向阀开启过程瞬时的流场、阀芯位移、液动力、von Mises应力分布和形变进行了对比。

液控换向阀；流固耦合；动网格；动态仿真

simulation

在各类液压系统中液控换向阀应用广泛，其性能影响着整个液压系统的工作。滑阀式换向阀的主要性能是平稳换向，迅速反应。滑阀内部流场、液动力以及动态响应特性是目前研究的热点。赵蕾等[1-3]利用计算流体动力学方法对液压滑阀开启过程或关闭时内部的流场分布及液动力进行了仿真分析，其中动态模拟时阀芯速度是预先给定，实际上滑阀开启中阀芯速度是不断变化着的。姜涛[4]对换向阀P-B通道(进行了动态仿真研究，换向阀的动态开启过程是通过假定阀芯不动来实现的，但在实际运行中阀芯和流体相互影响，需要考虑流固耦合的影响。张蕊华[5]对阀芯及其周围流场数值模拟时考虑了流固耦合，先对流场分析进行了计算，然后将数值结果加载到固体结构上，显然这种流固耦合的数值计算是单向的。在换向阀的实际工作中，换向阀的开合是一个动态过程，阀芯的运动及形变相反又会对流体运动产生重要影响[6]。

针对上述问题，将流固耦合理论和动网格技术相结合，以流体力学软件CFD-ACE+为平台，对3种不同节流结构的液控换向阀在弹簧力、驱动力及流体力作用下的开启过程进行动态模拟分析，为改善液压滑阀内部流体流动状态、动态响应特性和阀芯受力状况提供依据。

1 三维几何模型和网格划分

液控换向滑阀由多个阀体内腔组成，本文主要对其中的一个阀体内腔进行研究[7]。以P-B口开启过程为例，其结构示意图如图1所示，在出口节流处阀芯台肩上设有3种不同的节流结构。

借鉴朱钰[8]的简化方法，将液控换向滑阀阀芯两端部分及其附近流域略去，弹簧模型加载到阀芯一端。由于阀体内腔、流域和阀的内芯均以阀中央对称布置，为提高计算效率取流体区域和阀芯的对称作为研究对象。

在划分网格时采用高精度六面体结构网格，考虑流固耦合导致网格形变较大，三维瞬态流场解析误差太大，因此采用单一的网格变形方式，划分网格的变形能力和变形品质就很难控制。本研究将弹簧法和超限插值法联系起来处理结构网格的形变。基于分块网格的观点，将计算区域分成16个网格区。采取弹簧联系不同网格区的角点，通过弹簧启动各角点的形变[9]。3种不同节流结构的液控换向滑阀网格划分情况如图2所示，在阀芯出口台肩处为A、B、C 3种不同的节流结构。对节流处进行细化网格可以大大提高数值模拟结果的准确性。

图1 液控换向滑阀结构示意图

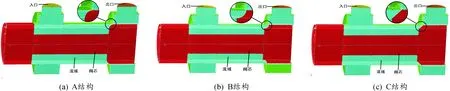
图2 网格划分

2 计算条件及参数设置

入口条件：压力入口，选取6 MPa；

出口条件：压力出口，设为大气压；

阀芯驱动压差：1 MPa；

弹簧刚度：80 N/mm；

液压油：型号VG46，密度ρ=890 kg/m3；运动粘度μ=46 mm2/s；设为不可压缩流体；

湍流模型：k-ε湍流模型。

仿真中不考虑温度、泄漏的影响，阀芯和阀体之间配合良好，无径向间隙，阀芯只考虑轴向位移。

3 仿真结果分析

3.1 阀芯运动情况分析

阀芯的运动影响因素主要是驱动力、液动力以及弹簧力。为验证数值计算结果的正确性，利用AMESim软件建立如图3所示的液控换向阀模型，与CFD-ACE+所建立的无节流结构理想滑阀模型仿真结果进行对比，两种软件仿真得到的阀芯位移、速度和加速度对比情况如图4所示。

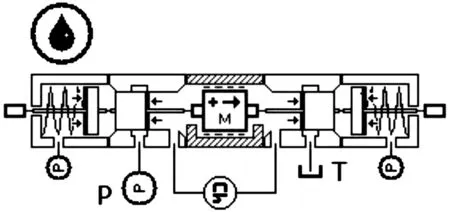
图3 液控换向阀AMESim模型

阀芯稳态位移的计算公式为：

(3)

式中：D为流道直径；xv为阀芯稳态位移；W为阀口的面积梯度；k为弹簧刚度；F为滑阀阀芯所受的驱动力；Fs为阀芯所受的稳态液动力；Δp为滑阀进出口压差；Δp1为驱动压差。

从式(3)，解得阀芯的稳态位移为0.71 mm，而CFD-ACE+和AMESim仿真的结果与理论计算值误差分别为3.1%和11.3%，CFD-ACE+的数值计算结果因考虑了流固耦合作用和流场微小流动带来的影响而更加精准。但因仿真条件的设置和理论计算的方法不可能完全一致，仍存在一定的误差。

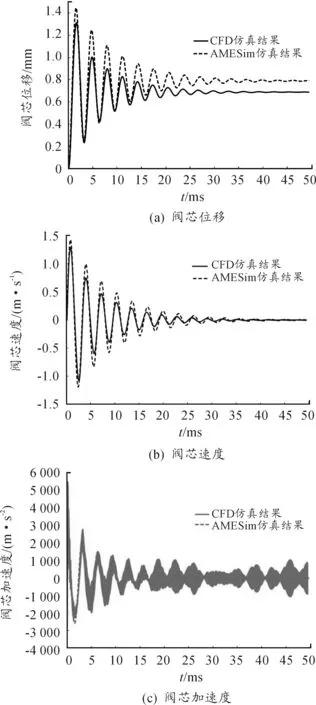
图4 CFD-ACE+和AMESim仿真结果

利用CFD-ACE+仿真得到的3种节流结构的液控换向阀阀芯位移随时间的变化情况如图5所示，假设当阀芯位移同一波动周期内波动幅度与该段波峰值之比小于0.5%时，即为稳态。

从图5可看出在液控换向阀P-B开启过程中，3种节流结构阀芯位移均存在一定的波动，超调量分别为45.9%、48.9%和48.7%，稳态位移分别为0.64 mm、0.59 mm和0.48 mm。A型超调量最小，稳态位移最大，达到稳态所需的时间也最短。

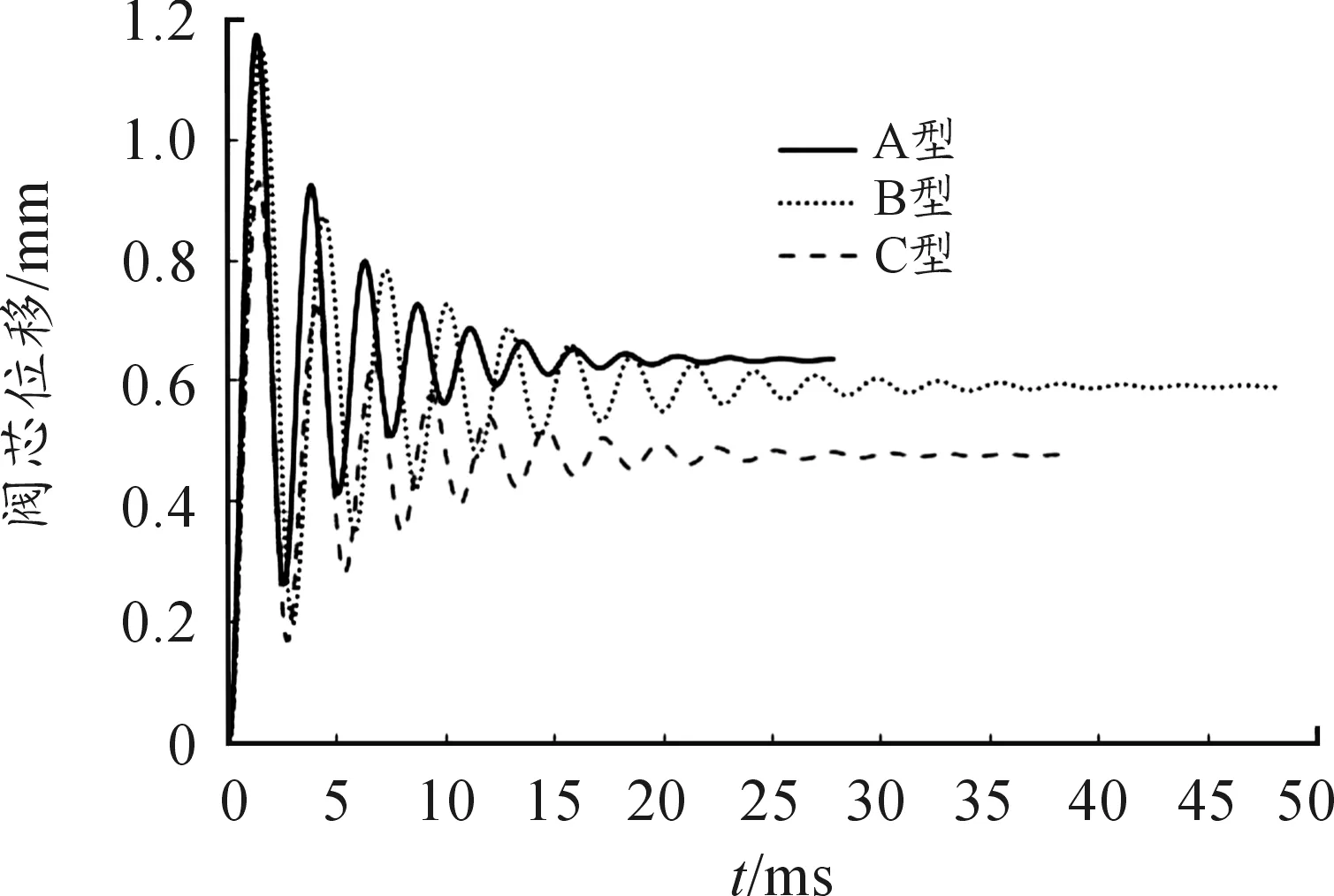
图5 阀芯开启过程的位移

3.2 液动力分析

滑阀阀芯表面所受到的轴向力可以由阀芯表面所受的压力对表面积积分得到，阀芯表面轴向力即为液动力[10-12]。图6给出了3种阀芯开启过程中所受液动力变化情况，包括瞬态液动力和稳态液动力，其中瞬态液动力等于不同瞬间总的液动力与稳态液动力之差。可知稳态液动力的大小均为负值，方向即为阀口关闭的方向。在阀芯开启过程瞬间，瞬态液动力变化较大，设计阀时须加以考虑。A型阀芯稳态液动力值最小，达到稳态所需的时间最短，但瞬态液动力波动峰值较大。

图6 阀芯开启过程液动力变化

3.3 流固耦合分析

图7给出了3种节流结构液控换向阀在开启初期、最大位移和稳态时流域的压力场和阀芯所受的冯.米斯应力场。冯·米斯应力是根据第四强度理论得到的一种当量应力，可以用来对疲劳、破坏等进行评价[13]。

图7 不同时刻压力场和应力场

从图7可以看出，在阀口节流区域靠近阀体的流场均会产生负压，其中B型阀芯负压区域较大。流场的负压导致产生气蚀。由于气蚀，阀芯则容易破坏。在入口靠近阀杆的流场均出现了高压区，这会对阀芯形成高压冲击，从而影响阀芯的径向平衡，容易造成阀芯卡死。3种节流结构阀芯所受冯.米斯应力值的分布基本一致，在阀芯台肩和阀杆连接处冯.米斯应力值均最大。图8为阀芯开启过程应力值的峰值随时间变化情况。从其中可知，阀芯开启过程最大冯.米塞斯应力值均存在波动，其中A型阀芯稳态值最小，B型阀体内芯稳态值和瞬态值最大。B型阀芯开启过程所受冯.米塞斯应力的峰值为35.5 MPa，阀芯材料(20CrMo)的抗拉、抗剪和抗压强度都大于200 MPa[14]，根据换向阀的强度理论，换向阀使用过程中的安全系数取为2，由此文中所研究的3种节流结构的阀芯强度均满足要求，设计时无需考虑阀芯的疲劳破坏。

图9给出了3种节流结构阀芯在开启初期、最大位移和稳态位移时阀芯的形变及其分布情况。

从图9可看出，阀芯的径向形变主要发生在阀杆上，最大形变分布位置和大小随时间不断变化。达到稳态时，阀杆在入口处靠近阀口方向和出口处背离阀口方向产生较大变形。稳态时3种节流结构阀芯的最大形变分布位置基本相同，B型阀芯最大形变较大，A型阀芯最大形变较小。

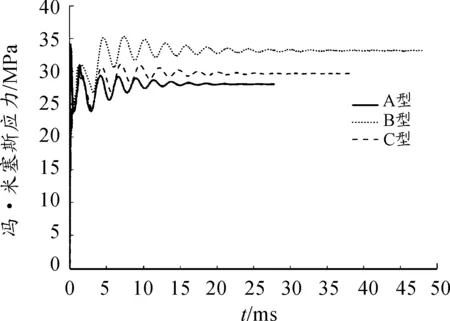
图8 阀芯开启过程最大冯·米塞斯应力值变化

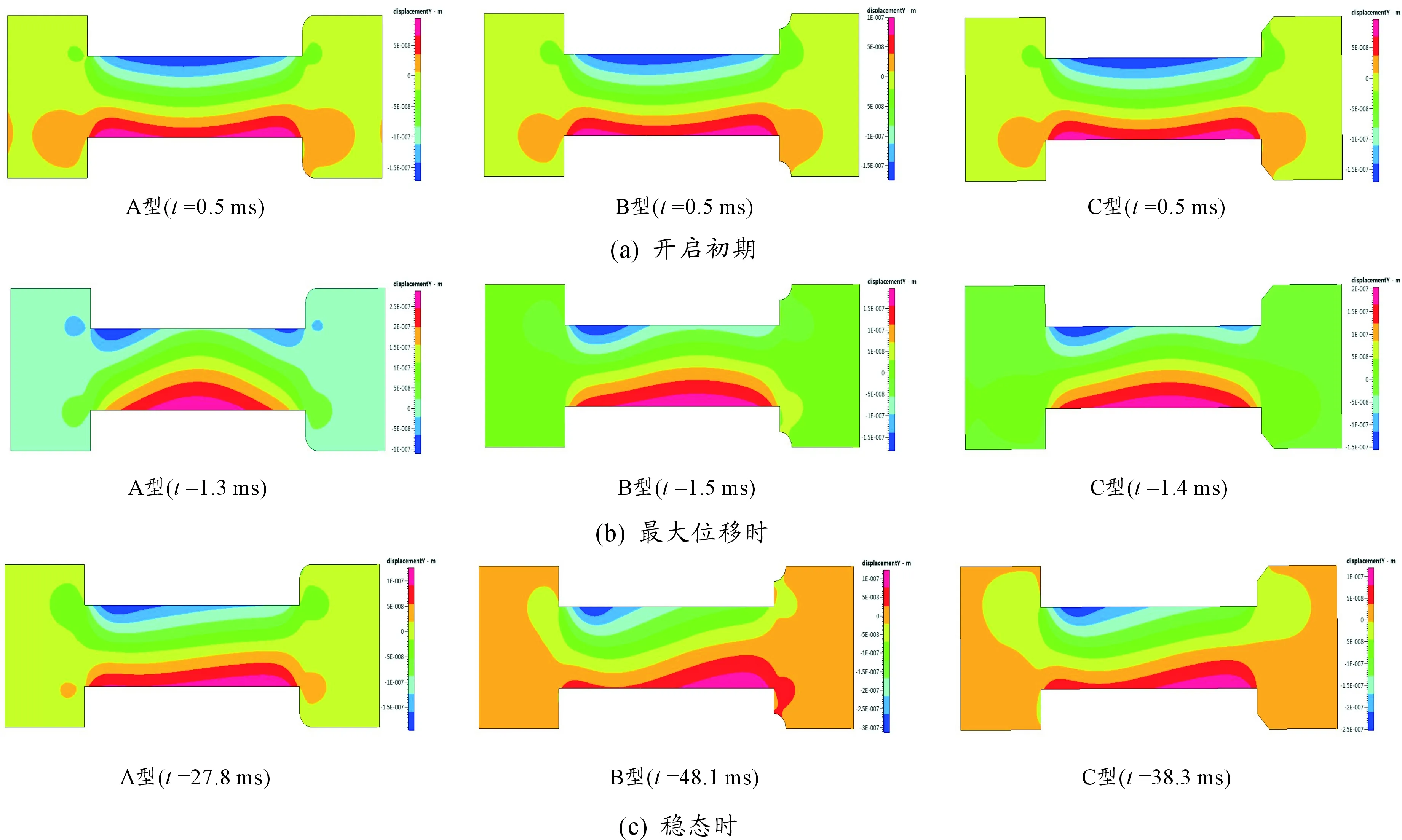
图9 不同时刻阀芯形变

4 结论

1) 液控换向阀开启时在阀口节流区域靠近阀体的流场产生负压区，在入口靠近阀杆的流场出现高压区；

2) 在阀芯开启同时，瞬态液动力值变动较大，冯·米斯应力最大值主要集中在阀芯台肩和阀杆连接处，设计阀时须加以考虑；

3) 稳态时3种节流结构阀芯的最大变形分布基本相同， A型阀芯最大变形较小；

4) A型阀芯在试验条件下达到稳态时位移最大，液动力、稳态冯.米塞斯应力值最小和位移超调量最小，时间最短，设计阀芯时可以考虑采用该节流结构。

[1] 赵蕾,陈青,权龙.阀芯运动状态滑阀内部流场的可视化分析[J] 农业机械学报,2008(11):142-145，155.

[2] 吴小锋,干为民,刘春节,等.液压换向滑阀内部结构的健壮性设计[J].中国机械工程,2015,26(15):2030-2035，2040.

[3] 杨科,金晓宏,肖鹏飞,等.非全周矩形开口滑阀小开口度时流量及液动力特性研究[J].流体机械,2016(7):14-17，62.

[4] 姜涛,黄伟,王安麟.多路阀阀芯节流槽拓扑结构组合的神经网络模型[J].西安交通大学学报,2016(6):36-41.

[5] 张蕊华,吴启帆,易健,等.压电驱动精密流量阀阀芯结构优化设计[J].润滑与密封,2016(5):97-101，107.

[6] 姜涛,夏明杰,王安麟.滑移网格法在滑阀三维瞬态流场解析的适用性分析[J].同济大学学报(自然科学版),2015(10):1575-1581.

[7] 刘罡,张俊俊,王江勇.基于ADINA液压滑阀的流固耦合研究[J].机床与液压,2012(23):158-160.

[8] 朱钰.液控换向阀内流场及动态特性的数值模拟[J].哈尔滨工业大学学报,2012(5):133-139.

[9] SINGHAL A K,ATHAVALE M M.Mathematical basis and validation of the full cavitation model[J].Journal of Fluids Engineering,2002,124:617-624.

[10] 何晓晖,孙宏才,程健生,等.基于动网格的液压阀阀芯启闭中的液动力分析[J].解放军理工大学学报(自然科学版),2011(5):491-495.

[11] 闫清东,刘博深,魏巍.基于动网格的冲焊型液力变矩器流固耦合分析[J].华中科技大学学报(自然科学版),2015(12):37-41.

[12] 张晓俊,权龙,赵斌.内流式滑阀壁面压力分布可视化计算及试验验证[J].机械工程学报,2016(14):196-203.

[13] 何晓晖,栾健,王强.基于CFD的液压锥阀开启过程流固耦合分析[J].液压与气动,2015(9):122-125.

[14] 李建心,刘效东.液动力对换向阀作用的ANSYS有限元分析[J].机床与液压,2010,38(17):119-120.

(责任编辑周江川)

TransientPropertiesofHydraulicOperatedDirectionalValveBasedonFluid-structureInteraction

ZHANG Shunfeng, ZHANG Sheng, WANG Qiang, HE Xiaohui, XU Lei

(College of Field Engineering, PLA University of Science & Technology, Nanjing 210007, China)

Three-dimensional CFD modals were established via CFD-ACE+ software based on fluid-structure interaction and dynamic mesh.The opening process of hydraulic operated directional valves under the spring force, driving force and flow force process were simulated and the results are consistent with the theoretical values and values calculated by AMESim.The transient flow fields, spool displacement, flow force, distribution of von Mises stress, deformation of three different throttle structure of hydraulic operated directional valves in the opening process were compared and analyzed.

hydraulic operated directional valve; fluid-structure interaction; dynamic mesh; dynamic

2017-04-23；

：2017-05-11

：国家自然科学基金项目(51175511)

张顺锋,硕士研究生,主要从事液压传动与控制研究。

王强，教授，主要从事液压传动与控制研究，E-mail：wangqiangjs@sohu.com。

10.11809/scbgxb2017.09.032

format:ZHANG Shunfeng, ZHANG Sheng, WANG Qiang, et al.Transient Properties of Hydraulic Operated Directional Valve Based on Fluid-structure Interaction[J].Journal of Ordnance Equipment Engineering,2017(9):151-155.

TH137

：A

2096-2304(2017)09-0151-05

本文引用格式：张顺锋，张胜，王强，等.流固耦合作用下的液控换向阀动态特性仿真[J].兵器装备工程学报，2017(9):151-155.