基于CoSaMP算法的信号冗余分析

金 秋,王宏艳，范欣妍

(中国人民解放军装备学院， 北京 101416)

【信息科学与控制工程】

基于CoSaMP算法的信号冗余分析

金 秋,王宏艳，范欣妍

(中国人民解放军装备学院， 北京 101416)

以稀疏表示理论为出发点，分析信号的压缩感知理论与传统Nyquist采样定理的理论对比结果，根据CoSaMP算法和IFFT信号重构结果，定性和定量地分析了信号内部冗余性与利用这种冗余特征进行减运算量处理的可行性，进一步探讨信号的非均匀化处理，包括分数域和分形等方法在信号处理领域的适应性。

非均匀化处理；稀疏表示理论；压缩感知；CoSaMP算法

20世纪90年代,信号处理领域出现了一种全新的划时代的处理方法——信号的稀疏表示[1]。稀疏表示理论的思想产生后给信号处理领域注入了活力，发展而来的压缩感知理论在各个方面都得到重大应用，使得信号处理的发展迈开大的步伐。信号的稀疏表示从一种全新的角度，揭示了将信息而不是其载体作为处理对象的可行性，用很少的数据量恢复出接近完整信息的能力，让它迅速在通信领域大放光彩。在信号处理领域，若采用经典的处理方法即用Nyquist采样定理处理信号，相对于稀疏表示理论对信号的处理，会表现出数据量较大的特点，减缓处理效率。稀疏表示理论所发展的压缩感知理论对信号的处理优势从本质上反映了信号内部有很大的相干性，本研究使用传统采样方法对信号进行IFFT与CoSaMP算法对信号的重构，从而对信号本身的信息进行稀疏性分析，进一步探讨了未来信号处理趋势，展示非均匀处理方法的优势。

1 稀疏表示理论

1993年Mallat提出，任何信号都可以用超完备字典表示，并且这个超完备字典越稀疏，其重构的信号越精确[2]。这表明，任何信号经过变换都具有稀疏性，如图1所示，让信号表现出稀疏性的关键就在于这个字典的建立。

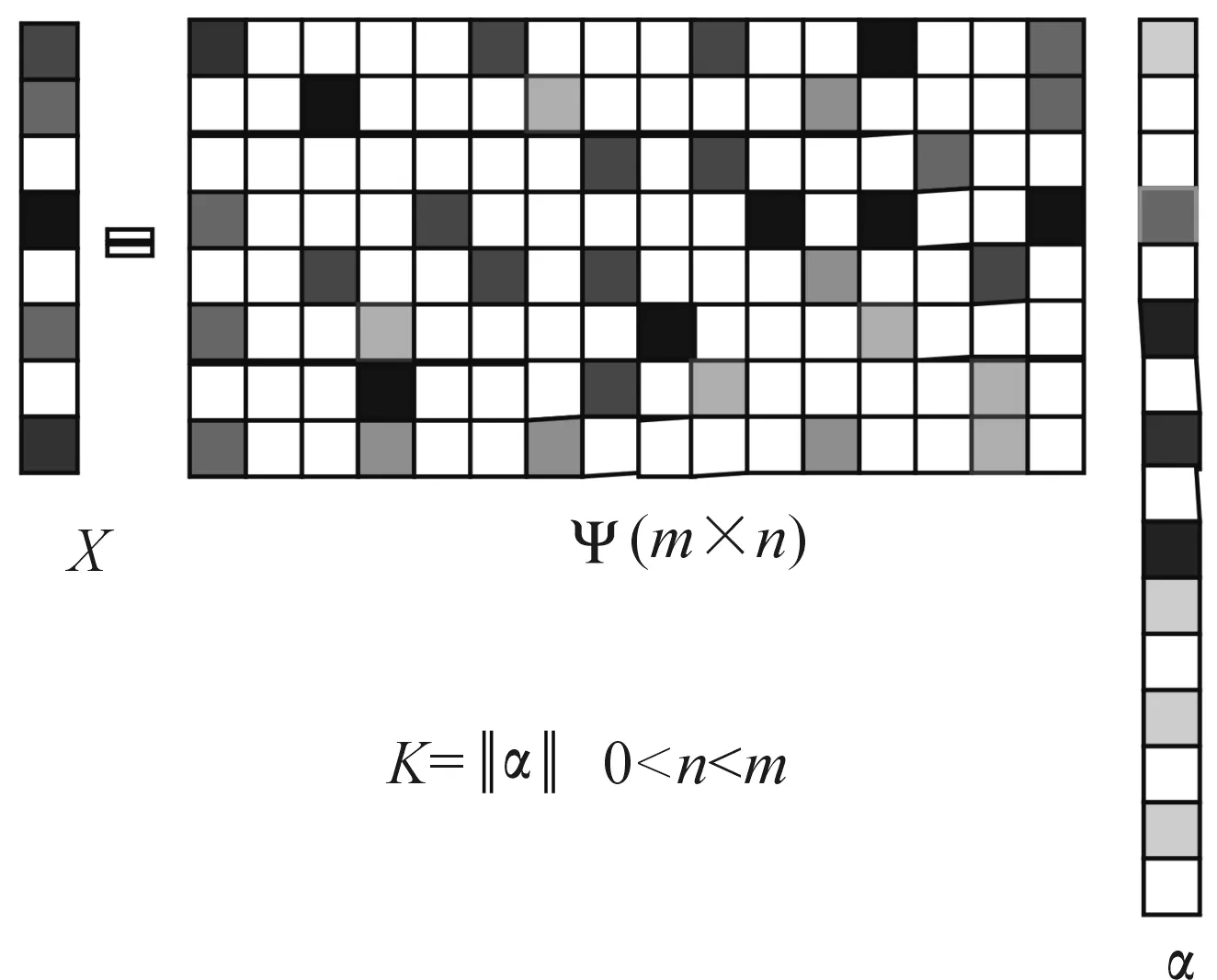
图1 信号的稀疏表示

根据信号理论，对于时域信号X∈Rm,可以用一组完备正交基Ψi∈Rm表示

(1)

其中：α为n×1的系数向量；Ψ=[Ψ1,Ψ2,…,Ψn]为一组完备基，若式(1)中αn仅有k个元素不为零，则认为信号X在Ψ上稀疏，并称Ψ为信号X的系数字典。

受Ψ维数影响，此时α中系数必然大多数不为0，所以α定是非稀疏的。将信号分解为n个m维向量Ψj∈Rm，j=1,2,…,n(n>m)的线性组合

(2)

此时对于Ψ=[Ψ1,Ψ2,…,Ψn]∈Rm×n(n>m)来说，n个向量不可能是正交基，必然存在线性相关。为了和式(1)情况下的基区分开来，式(2)情况下的列向量通常被称作框架或者原子，很显然，原子的集合是冗余的，是过完备的。过完备的框架所组成的矩阵Ψ=[Ψ1,Ψ2,…,Ψn]∈Rm×n(n>m)被定义为字典或者库[3]。字典Ψ=[Ψ1,Ψ2,…,Ψn]∈Rm×n(n>m)中行小于列，其秩为m。

式(2)由于其过完备性特点可得出一个过完备方程，所以在求信号的稀疏解时可以得到无穷多解，如何在这无穷多解中寻找到一个最符合要求的解，便成为信号稀疏化的重点。常用方法是通过矩阵的和范数进行匹配追踪(MP)或者基追踪(NP)等方法进行优化求解，达到用极少系数的稀疏Ψ来表示信号的目的[4]。

2 稀疏表示理论的信号感知应用与传统采样方法比较

2.1压缩感知理论

稀疏表示理论的应用在信号处理过程中发展为压缩感知(CS)理论。压缩感知理论包含信号稀疏表示、信号的非相干检测以及信号重构算法等3个核心内容[5]。对信号X进行时域观测，则有

Y=ΦX

(3)

其中Φ∈Rm×n为观测的矩阵，Y∈Rm×n为观测所得的观测值。由于方程欠定，所以不能够用测量值Y求得信号X。故将式(2)代入式(3)，可得

Y=ΦX=ΦΨα=θα

(4)

由于是稀疏的，可通过稀疏优化求解

min‖α1‖s.t.Y=θα

(5)

用基于范数来求解信号的最优化解，信号同样可以重构[6]，目前已经拓展为算法的优化求解。

2.2Nyquist采样定理

美国电信工程师H.奈奎斯特于1928年提出：当信号函数f(t)的最高频率分量为fm时,f(t)的值可由一系列采样间隔小于或等于1/(2fm)的采样值来确定,即采样点的重复频率f≥(2fm)[7]。这为均匀化的采样提供了一定程度的约束，在迄今为止的很长一段时间内，为信号采样频率和带宽设置提供了基本的指导。

2.3 对比分析

传统重构方法主要是利用对满足Nyquist采样定理的信号采样值进行IFFT变换，其效果相当于用采样值个数的sinc函数去逼近原始函数，在本质上对均匀采样值进行了遍历运算，无论能量集中还是冗余量，其依据为信号的连续性以及有限带宽。而基于稀疏理论的CS重构信号的算法则是利用信号经过变换和处理后产生的稀疏性，通过信号的另一种表示，对信号所用到的数据进行压缩和选取，通过较少的关键信息最优化获得更好的恢复效果[8]。特别对分布于高频段的信号处理时，用传统方法进行采样会使得采样带宽更加宽大，采样结果产生大的冗余，浪费了很大带宽。如若根据信号在其他表示方法下获得稀疏性表示，采用CS方法能更好地处理[9]。理论上信号均能通过运算获得稀疏性，在实际应用中大部分信号也可压缩，所以CS方法具有很大的应用前景。

3 CoSaMP算法信号重构

本节专门通过介绍基于压缩感知的压缩采样匹配追踪(CompressiveSampling MP)算法[10]以为下节仿真实验奠定基础。该算法是D.Needell提出的重构算法，算法本质是一种贪婪算法，其算法流程[11]为

输入：稀疏度K，恢复矩阵θ,测值Y

1) 初始赋值：r0=y，V0=[ ],t=1;

2) 求2K个最大匹配时原子的索引：

|rt-1,θj|, 2k};

3) 构建候选集：C=Vt-1∪B;

算法流程如图2所示。

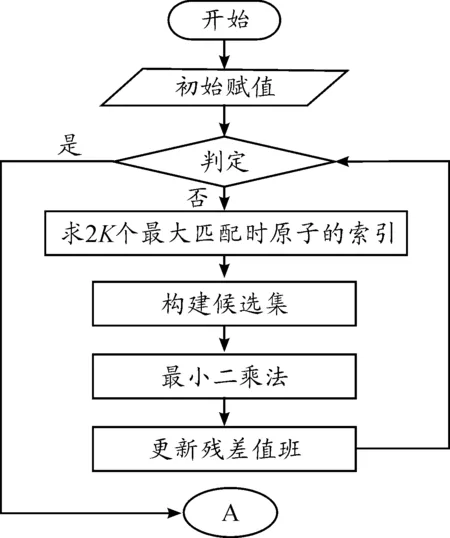
图2 CoSaMP算法流程

基于压缩感知的CoSaMP算法在一定稀疏度下，可以做到在信号的低数据处理量下对信号进行采集重构。

4 实验仿真

4.1 IFFT与CoSaMP算法信号重构

4.1.1 IFFT重构

生成稀疏度K=30，长度N=1 000的信号，观测信号长度M=200，如图3所示。对得到的信号进行频域分析，得图4所示的频谱。

图3 稀疏信号的产生

图4 信号频谱

计算信号频谱，并使用IFFT对信号进行还原，结果如图5。

图5 频域傅里叶反变换

通过仿真产生出拥有复杂频谱的信号，并对其进行IFFT变换，记录5次仿真的恢复残差和对应数据的L1范数，如表1所示。

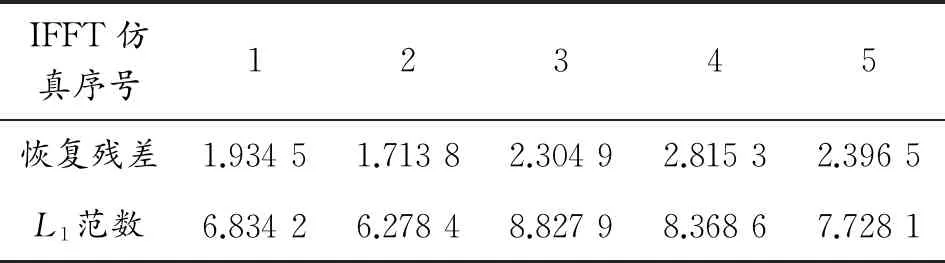
表1 IFFT仿真数据

从实验所得的仿真数据可以看出，传统处理方法对信号的恢复残差平均值为2.233 0，信号变换过程中所利用的数据量用L1范数衡量，计算得出IFFT变换所使用一维L1信号范数平均值为7.607 4。

4.1.2 CoSaMP算法信号重构

产生与图3同样约束的信号，并进行CoSaMP算法重构，重构结果如图6示，记录5次仿真的恢复残差和对应数据的L1范数，如表2所示。

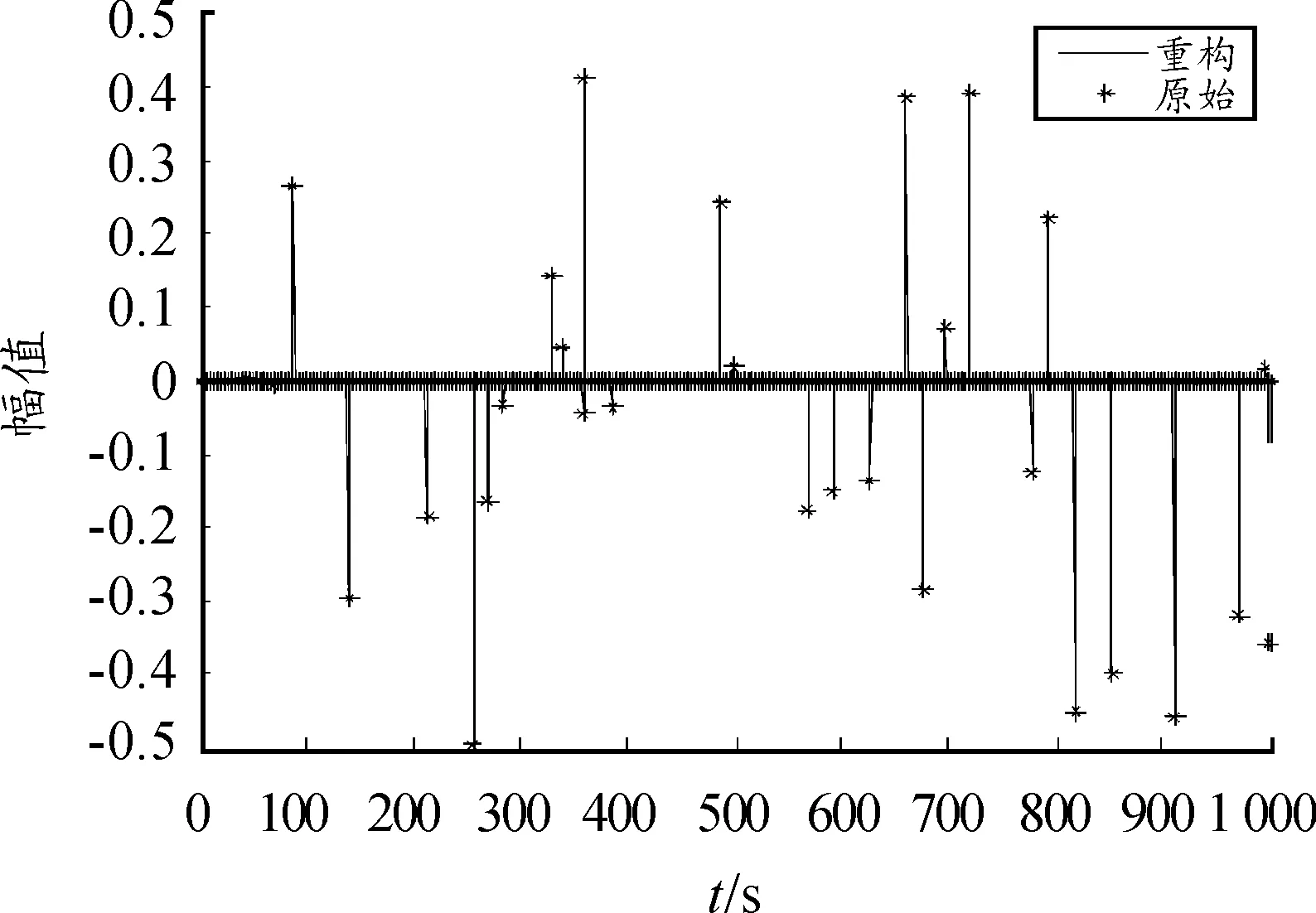
图6 CoSaMP算法

CoSaMP算法对信号的恢复残差平均值为1.493 2e-15。与第4.1节中IFFT恢复残差相差非常之大，说明应用基于压缩感知理论的CoSaMP算法对于复杂带宽信号有着非常突出的优势，在信号处理上有着更小数量级的误差。

通过CoSaMP算法所使用的信号L1范数平均值为1.542 1，相差4.933倍。换言之，使用CoSaMP算法大大的减少了运算和恢复所使用的数据量。传统采样利用脉冲串函数进行均匀采集，对于能量集中频谱复杂的信号处理显得捉襟见肘，而CoSaMP算法在较少数据量的条件下得到了低于传统采样很大误差的重构信号，说明了压缩感知信号的巨大优势，也说明了信号采集过程中本不需要很多的采集量，说明信号本身具有巨大的冗余。

表2 CoSaMP算法仿真数据

4.2CoSaMP算法重构范数与误差关系分析

由图7可知，CoSaMP算法重构信号所使用数据的L1范数与恢复残差之间有粗略的相关性，表现为L1范数越小，恢复残差越小。根据式2.3可知，通过极小化变换系数L1范数即最优化条件下的稀疏解，矩阵Θ就可以更好地满足用来估计原始信号的约束条件。

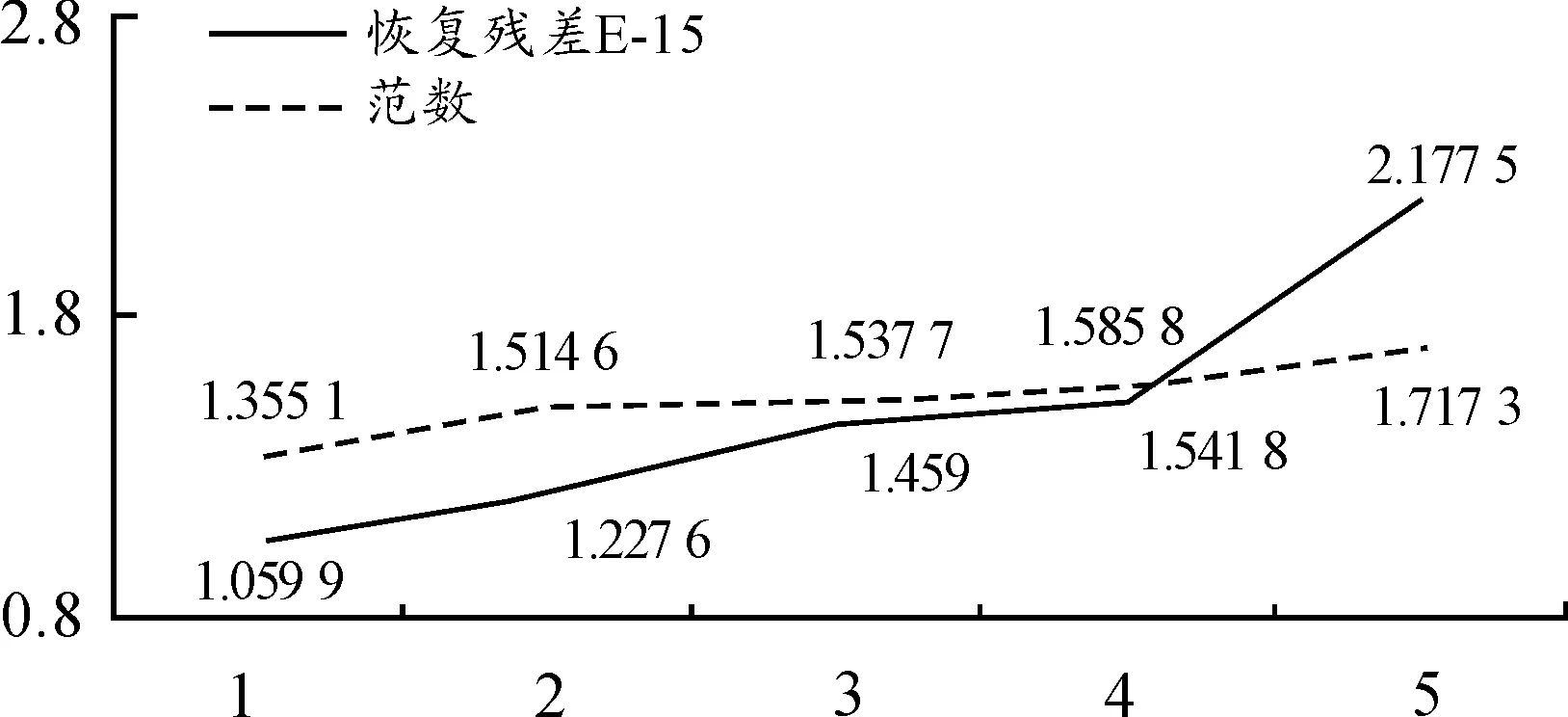
图7 4.1.2实验次数及对应数据折线

4.3 基于仿真实验的理论拓展分析

CS中对数据的获取，与传统意义上利用脉冲串函数均匀采集数据的方法截然不同。信号的稀疏程度越高，恢复出原始信号所需的运算量越少，也就是感知量越少，通过这一点极大地提高了信号处理和感知的速率。一般来说，信号中能量或功率集中的部分，携带着信号的绝大部分信息。信号的稀疏处理实际上揭示了信号信息间的极大相干性，将信号从形式和数学处理进一步扩展为对信号所携带的信息的直接处理。从另一个角度来看，对于高冗余的目标使用非均匀手段，针对其特定的信息进行提取，能使目标的利用率得到很大提升。用非均匀的手段解决问题，适用于信息在信号中的分布特点，往往使工作事半功倍。

5 结论

压缩感知理论针对于信号处理在一定程度上打破了经典采样定理的束缚，无论是在信号图像，还是其他领域，这种方法也给我们一定的启示。比如，均匀的处理方法可以得到信号信息，但是往往要付出大的计算量和冗余空间的代价。真正的高效处理问题，就要在问题内部寻找其重点部分。信号的冗余性使我们认识到，信号内的信息有很大的相干性和自相似性，所以稀疏理论和分形理论[12]等非均匀处理方法必然可以在该领域有所作为。

目前针对信号中含载信息的处理方法越来越受到关注。虽然在效果上非常显著，但这种寻找最优表示方法在使用过程中需要很多条件。实践始终在接近理论，但是还是有一定出入，为下一步的研究加上了斯芬克斯式困难。在未来高精尖的研究中，非均匀、非平稳、非理想状态的处理和运算方式必然取代均匀、平稳、理想状态的思维推论，有望成为常态。

[1] 何昭水,谢胜利,傅予力.信号的稀疏性分析[J].自然科学进展,2006(9):1167-1173.

[2] MALLAT S,ZHANGZ.Adaptive time-frequency transform[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing:Digital Speech Processing.IEEE Computer Society,1993:241-244.

[3] 谢浪雄.稀疏表示理论及其应用研究[D].广州：广东工业大学,2015.

[4] 赵亮.信号稀疏表示理论及应用研究[D].哈尔滨：哈尔滨工程大学,2012.

[5] 江海,林月冠,张冰尘,等 基于压缩感知的随机噪声成像雷达[J].电子与信息学报,2011(3):672-676.

[6] 高雪.基于压缩感知的图像重构算法研究[D].哈尔滨：哈尔滨理工大学,2015.

[7] 奥本海姆,谢弗,董士嘉,等.数字信号处理[M].北京:科学出版社,1980.

[8] DONOHO D L.Compressed sensing[J].IEEE Trans.on Information Theory,2006，52(4)：1289-1306.

[9] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.

[10] NEEDELL D,TROPP J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J].Applied & Computational Harmonic Analysis,2009,26(3):301-321.

[11] 郎利影,王勇,白文庆,等.基于压缩感知CoSaMP算法的精确重构[J].计算机应用研究,2015,32(8):2554-2557.

[12] 孙洪军,赵丽红.分形理论的产生及其应用[J].辽宁工学院学报,2005(2):113-117.

(责任编辑杨继森)

SignalRedundancyAnalysisBasedonCoSaMPAlgorithm

JIN Qiu， WANG Hongyan, FAN Xinyan

(Academy of Equipment Command & Technology of PLA, Beijing 101416, China)

Aiming at the expansion of the new method of signal processing, from the sparse representation theory as the starting point, combining the signal compression perception theory with the traditional Nyquist sampling theorem, the internal performance of the signal is a great redundancy, and through CoSaMP Algorithm and IFFT transform, the results are analyzed and compared.The feasibility of the internal redundancy and the redundancy processing are analyzed qualitatively and quantitatively.Further, the nonuniformization of the signal includes fractional domain and fractal method will be in the signal processing and will be a great development.

nonuniformization; sparse representation theory; compression perception; CoSaMP algorithm

2017-04-20；

：2017-05-20

金秋(1995—)，男，硕士研究生，主要从事通信与信息工程研究。

10.11809/scbgxb2017.09.026

format:JIN Qiu，WANG Hongyan, FAN Xinyan.Signal Redundancy Analysis Based on CoSaMP Algorithm[J].Journal of Ordnance Equipment Engineering,2017(9):126-129.

TN911.7

：A

2096-2304(2017)09-0126-04

本文引用格式：金秋,王宏艳，范欣妍.基于CoSaMP算法的信号冗余分析[J].兵器装备工程学报，2017(9):126-129.