基于模型参考自适应控制的伺服定位系统研究

严尚贤，蒋晓辉

(中国兵器装备集团自动化研究所 装药中心， 四川 绵阳 621000)

【信息科学与控制工程】

基于模型参考自适应控制的伺服定位系统研究

严尚贤，蒋晓辉

(中国兵器装备集团自动化研究所 装药中心， 四川 绵阳 621000)

针对永磁同步电机提出采用模型参考自适应控制策略进行伺服定位控制仿真研究；建立李雅普诺夫函数，设计了由控制对象的输入和输出构成的模型参考自适应控制规律，该控制策略能够解决非线性、时变系统带来的不确定性，提高伺服电机的位置控制性能；仿真研究结果表明：该自适应律能以优异的性能完成定位跟踪任务，控制效果较好。

永磁同步电机；模型参考自适应控制；伺服定位；李雅普诺夫稳定性理论；自适应律

永磁同步电机(PMSM)是一类具有多变量、强非线性、高耦合性、时变等特点的被控对象[1]，经典的控制策略在模型参数匹配较好的情况下，能取得不错的控制性能。而电机在实际运行中，它的各项参数是随着环境变化的，考虑负载转矩和电阻等参数的不确定性，难以获得准确的数学模型，常规的控制方式无法保证控制精度[2-3]。

模型参考自适应控制主要思想是：根据期望的控制目标，选取性能优异的参考模型，通过调整自适应参数，使被控对象跟踪参考模型，达到与参考模型一样的控制效果[4]。本文基于李雅普诺夫稳定性理论[5-6]，设计出了一套模型参考自适应律，该控制策略能够解决永磁同步电机参数随环境变化的不确定性问题，达到伺服定位，提高了电机位置控制的性能。

1 PMSM模型参考自适应控制器设计

本文提出了采用李雅普诺夫第二法推导模型参考自适应系统的控制规律，保证在系统全局渐进稳定下的自适应控制[7]。控制系统可用状态方程或传递函数描述。控制系统用状态方程描述时，可用系统的状态变量构成自适应规律；控制系统用传递函数描述时，可用系统的输入变量和输出变量构成自适应规律。但对许多实际控制对象往往不能获得全部状态变量，因此提出采用控制对象的输入输出构成自适应控制规律[8]。

本文采用三环伺服位置控制系统[9-11]，各补偿器采用PID控制，推导出PMSM定位系统的数学模型。推导过程略去，取最终的闭环传递函数：

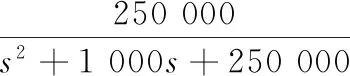
(1)

设定期望的控制性能为：在阶跃给定信号作用下，系统输出响应无超调，调节时间0.15 s左右。设计参考模型：

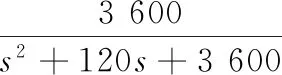
(2)

整个模型参考自适应闭环控制系统结构如图1所示。

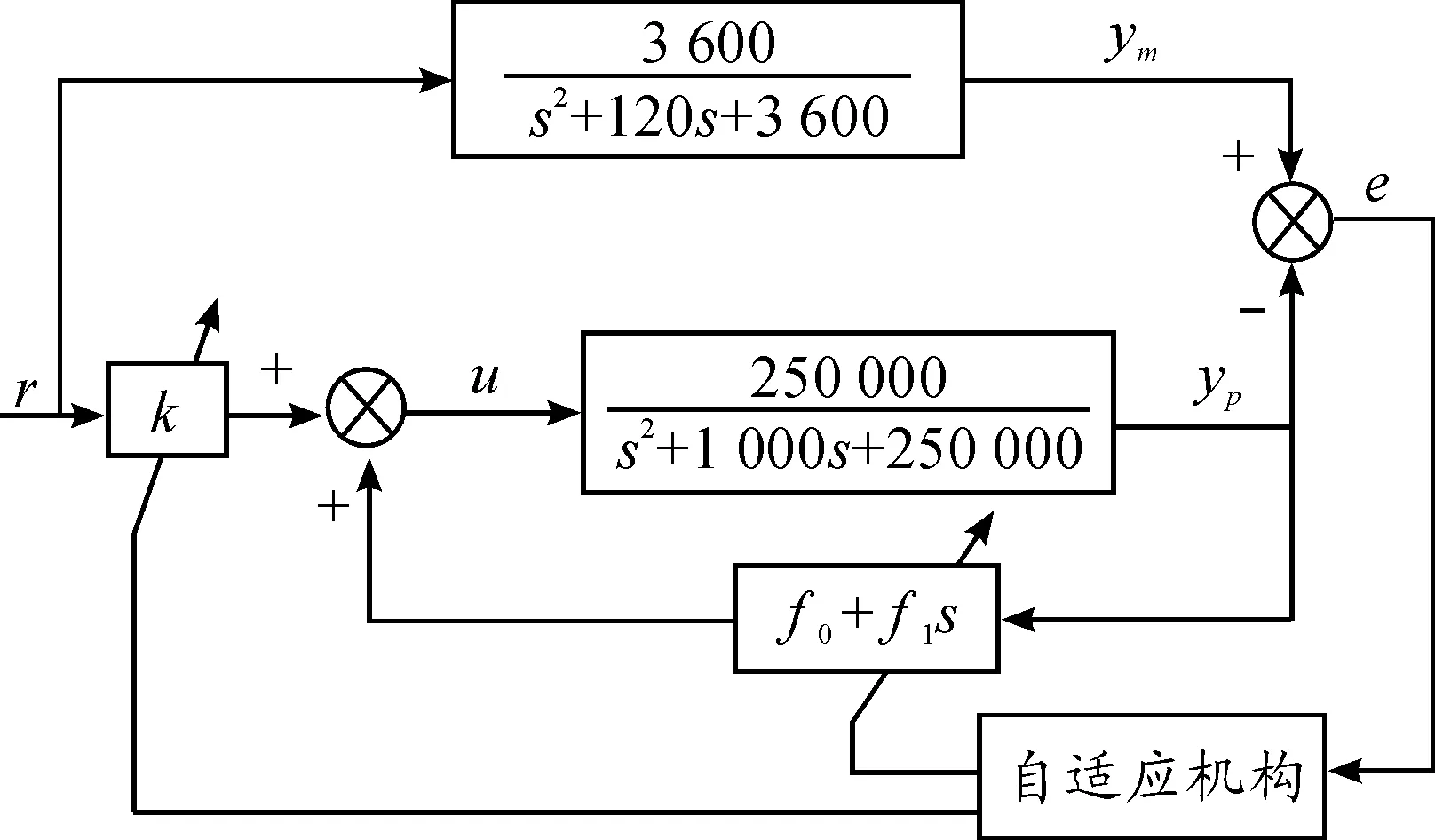
图1 模型参考自适应系统结构

根据控制对象，其微分方程为

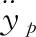
(3)

选取控制变量为

(4)

式(4)中，k为前馈增益，f0和f1为反馈增益，通过自适应调整参数k、f0和f1使控制对象的输出跟踪参考模型的输出。所选取的参考模型的阶数与控制对象相同，其微分方程为

(5)

式(5)中，r为参考模型的输入信号。

将式(4)代入式(3)，可得可调系统微分方程：

250 000(1-f0)yp=250 000kr

(6)

令

a=1 000-250 000f1

b=250 000(1-f0)

c=250 000k

(7)

则式(6)可写为

(8)

设e=ym-yp为广义误差，由式(5)和式(8)可得误差方程：

(b-3 600)yp+(3 600-c)r

(9)

令

δ1=a-120，δ0=b-3 600，σ=3 600-c

(10)

则式(9)可写为

(11)

设参数误差向量φ和广义误差向量ζ分别为

(12)

则误差方程式(11)可写为矩阵-向量形式：

(13)

式(13)中

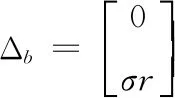
(14)

选取李雅普诺夫函数为

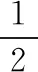
(15)

式(15)中，p为2×2正定矩阵，Γ为3维正定对角矩阵，即：

Γ=diag(1,1,1)

(16)

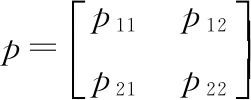
(17)

PA+ATP=-Q

(18)

且

(19)

则自适应规律为

(20)

(21)

(22)

由式(7)和式(10)，可得：

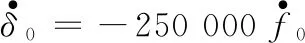
(23)

将式(20)、式(21)、式(22)代入式(23)得：

(24)

(25)

(26)

将矩阵A和Q代入式(18)可得：

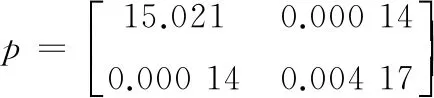
所以：

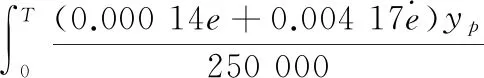
(27)

(28)

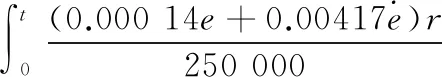
(29)

按式(27)、式(28)、式(29)自适应调节可调参数f0、f1、k，可使yp→ym。其中，f0(0)、f1(0)、k(0)为自适应律初值。

理论上自适应规律中的可调参数初值可选为任意常数值。但如果初值选取不当，可能使系统处于不稳定的初始状态。有的情况下，通过可调参数的自适应调整能使系统脱离不稳定状态，而有的情况下，可能在自适应规律使系统脱离不稳定状态之前，系统已经发散得不能继续工作，所以自适应规律中的可调参数初值最好在理想参数附近选取。

模型参考自适应系统处于稳定状态时，有：

(30)

将式(30)代入式(4)可得：

k(0)+f0(0)=1

(31)

由式(31)再结合仿真实验，即可确定使系统处于稳定状态的自适应规律的初值。

2 PMSM模型参考自适应控制器仿真研究

为了验证所述模型参考自适应控制策略的有效性，在Matlab/simulink平台上对所推导的自适应律进行仿真研究。

首先研究未施加模型参考自适应控制策略时，参考模型和被控对象对阶跃输入信号的响应特性。输出曲线如图2所示。

图2 单位阶跃响应输出曲线

为说明模型参考自适应律的有效性，本文选取两个差异较大的数学模型作为研究对象。从仿真结果可知，被控对象与参考模型的输出特性差异明显，被控对象响应快但存在一定的超调，参考模型响应平缓且无超调，两者之间位置响应误差较大。

然后对上述研究对象施加模型参考自适应控制策略，由式(31)结合仿真实验，确定自适应律理想初值如下：

k(0)=0.35，f0(0)=0.65，f1(0)=-0.006

1) 选取理想初值，给定单位阶跃信号，仿真波形如图3和图4所示。

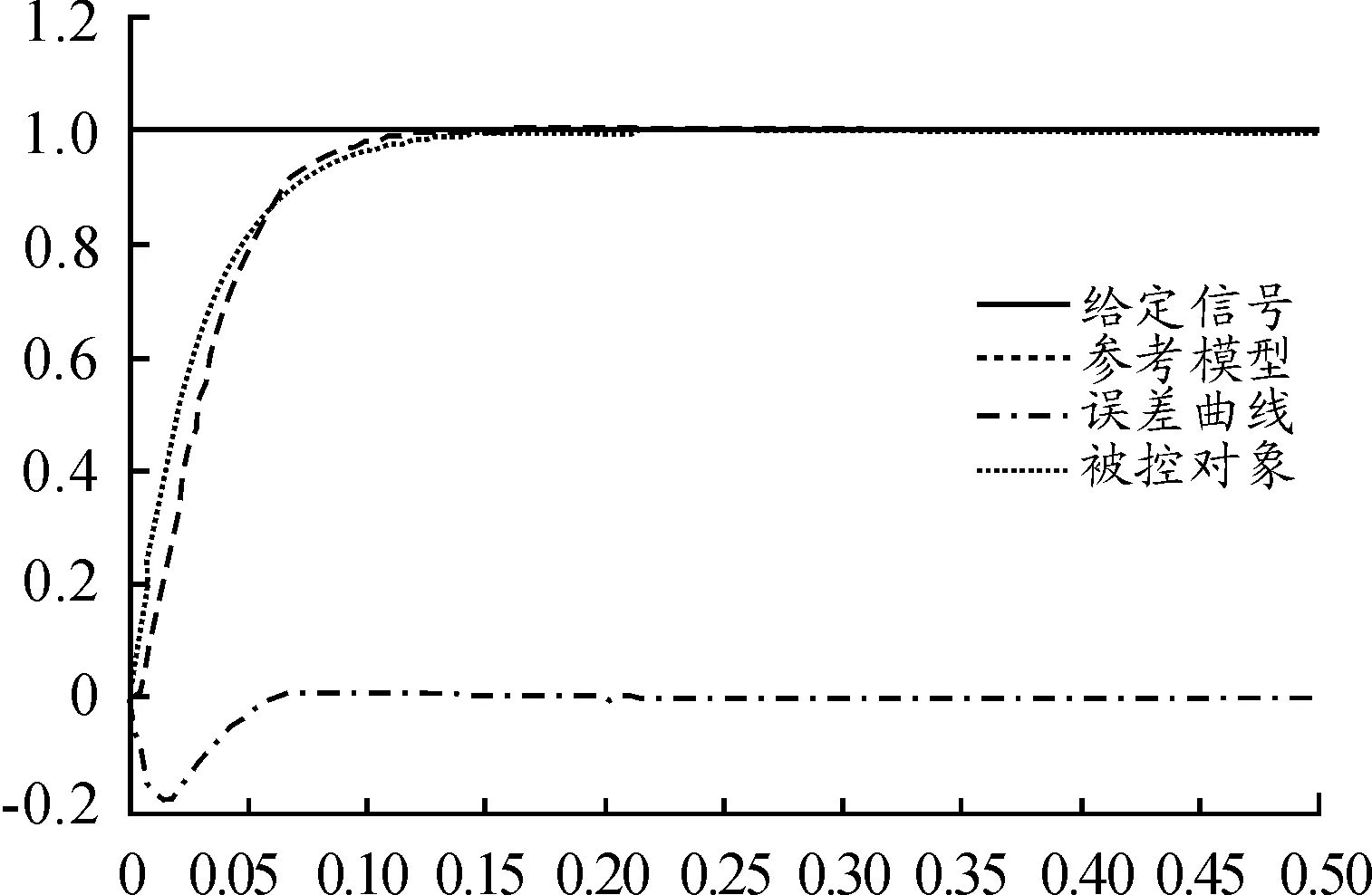
图3 单位阶跃响应输出曲线

图4 自适应参数调整曲线

由仿真实验可知，开始阶段，被控对象与参考模型之间存在一定的跟随偏差。在自适应参数的调整下，两者的误差逐渐趋于零，表明本文所设计的模型参考自适应系统能够使被控对象跟随参考模型。系统根据自适应律在线调整可调参数，使得模型跟踪偏差趋于零，系统响应无超调，在0.1 s跟随参考模型，在0.15 s达到跟随给定的状态，符合预期期望的动态指标。从参数自适应调整曲线可知，所选取的初值与理想初值一致，则可调参数在自适应调整的过程中基本不变。

2) 选取理想初值，给定360°的位置阶跃信号，仿真波形如图5和图6所示。

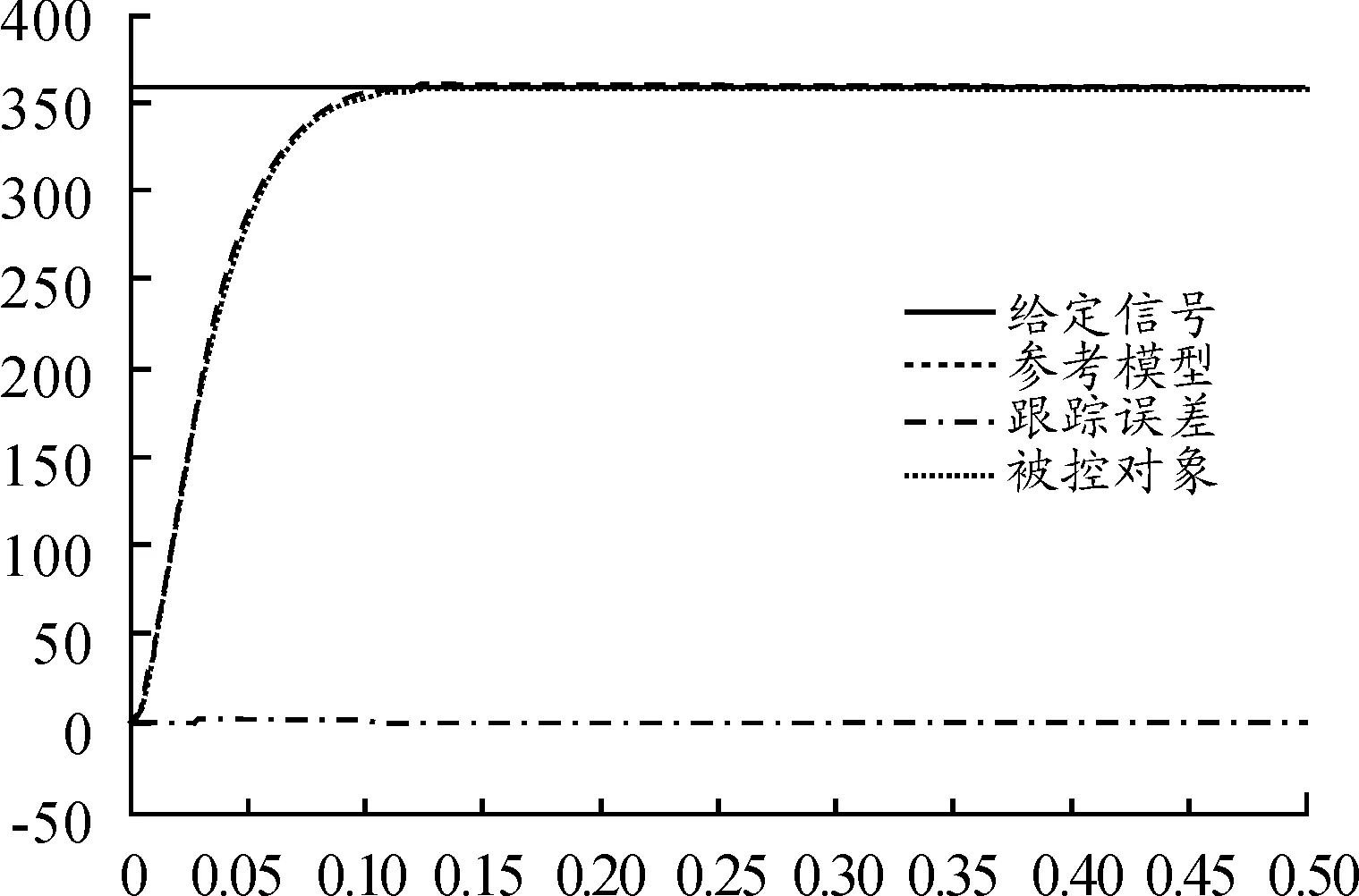
图5 位置阶跃响应输出曲线(r=360°)

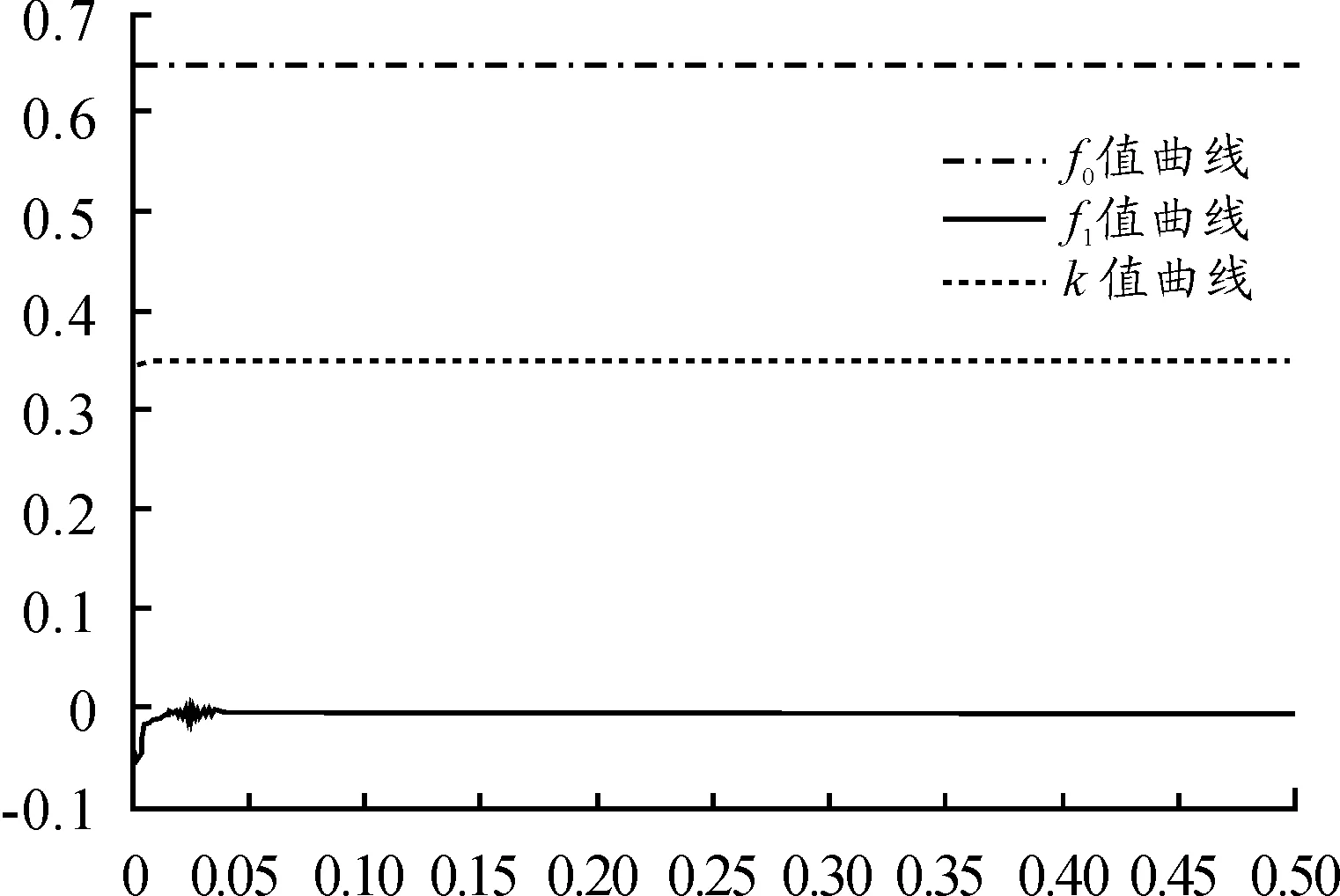
图6 自适应参数调整曲线(r=360°)

从仿真曲线可知，给定360°的位置阶跃响应，被控对象的输出与参考模型的输出基本一致，跟踪效果好，响应无超调，在0.12 s即可达到给定值。在起始阶段，由于位置跨度较大，自适应系统迅速调整可调参数，跟踪参考模型。

3) 当自适应律初值选取不在理想值附近时，检验系统能否跟踪参考模型。取自适应律初值如下：

k(0)=0.4，f0(0)=0.7，f1(0)=-0.01

选取初值之后，给定360°的位置阶跃信号，仿真波形如图7和图8所示。

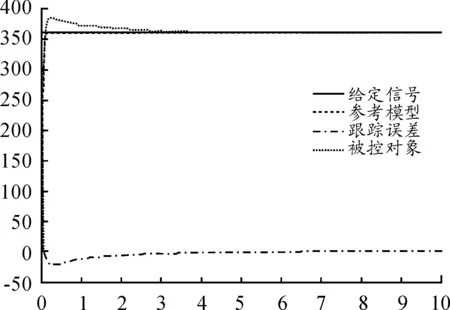
图7 位置阶跃响应输出曲线(非理想初值)

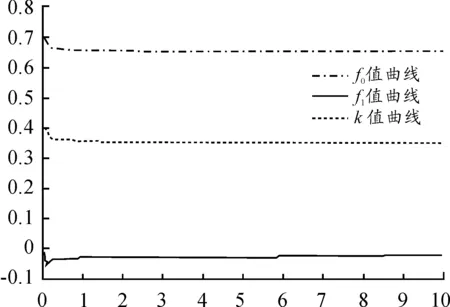
图8 自适应参数调整曲线(非理想初值)

由仿真曲线可知，自适应调整参数给定初值为非理想值时，被控对象的输出存在超调，调节时间3 s。起始阶段，跟踪参考模型效果较差，误差也较大，但最终也能趋于给定值，达到稳定状态。从可调参数曲线可以看出，k值由0.4→0.35，f0值由0.7→0.65，最终达到理想状态。

4) 当PMSM位置控制系统参数发生变化时，其数学模型传递函数也随之变化。现选取被控对象传递函数为

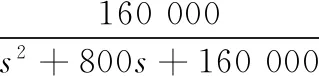
选取自适应律初值为理想初值，即：

k(0)=0.35，f0(0)=0.65，f1(0)=-0.006

给定360°的位置阶跃信号，仿真波形如图9和图10所示。

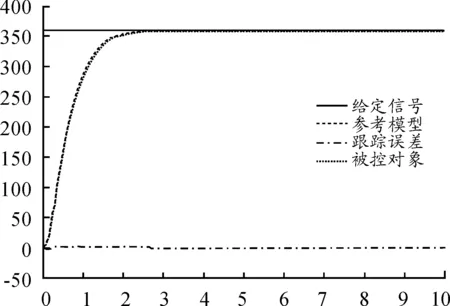
图9 位置阶跃响应输出曲线(变控制对象)

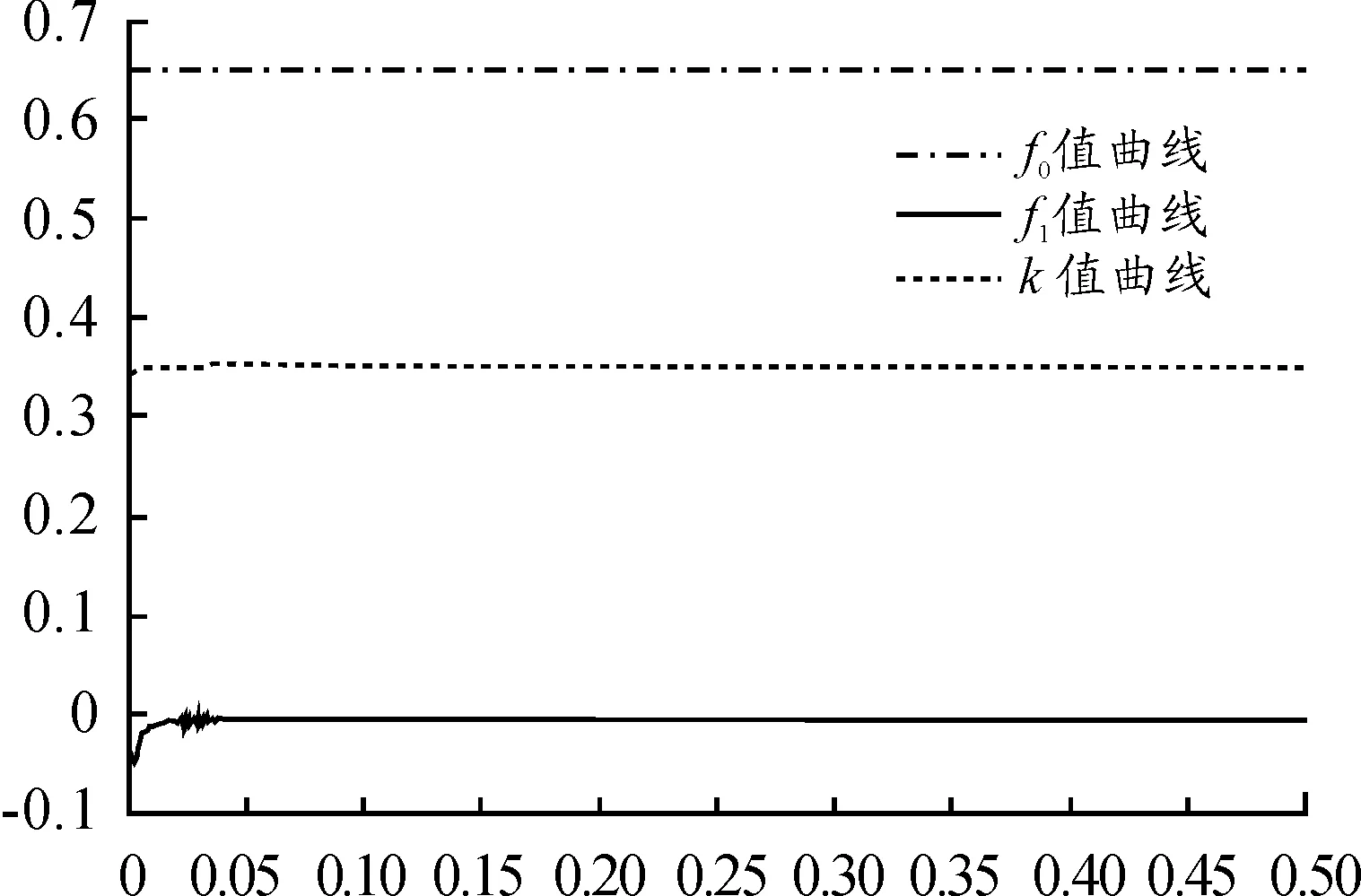
图10 自适应参数调整曲线(变控制对象)

从图9和图10可以看出，改变控制对象模型之后，本文所设计的模型参考自适应系统依然有效，被控对象能够紧密跟随参考模型，满足控制要求。在实际生产运行中，该套控制系统对电机参数变化具有自适应调节可调参数的功能，能很好的解决电机数学模型随环境变化带来的不确定性难题。

由仿真验证基于李雅普诺夫稳定性理论的模型参考自适应控制策略的正确性，自适应系统通过调整自适应参数，控制被控对象跟踪参考模型，达到与参考模型一样的控制效果。

3 结论

针对PMSM的特点，本文提出采用模型参考自适应控制策略，选取期望性能的参考模型，控制被控对象跟踪参考模型的输出。根据李雅普诺夫稳定性理论，设计了一套由控制对象的输入、输出构成的自适应控制规律，并在simulink仿真平台上对控制策略进行了仿真实验。仿真结果表明：该自适应律能以优异的性能完成定位跟踪的任务。

[1] 李泽明,周建洪.永磁同步电机三环交流伺服系统的仿真研究[J].科技创新与应用,2015,32(6):5-6.

[2] 史敬灼,张慧敏.行波超声波电机Lyapunov模型参考自适应转速控制[J].电工技术学报,2011(4):44-50.

[3] 柯希彪,鲁怀伟,李鹏飞.基于模糊变结构模型参考自适应观测器的永磁同步电机控制[J].电机与控制应用,2016(12):24-30.

[4] 常凯.基于模型参考自适应的永磁同步电机无速度传感器控制系统的设计[D].沈阳:东北大学,2009.

[5] 任斌,程良伦.李雅普诺夫稳定性理论中V函数的构造研究[J].自动化与仪器仪表,2009(2):8-10,49.

[6] 曹淼龙,李强.基于李雅普诺夫稳定性的PID控制器参数整定与应用比较[J].机床与液压,2013(5):142-144.

[7] 朱美玉,尤晓琳.李雅普诺夫稳定性理论应用研究[J].河南师范大学学报(自然科学版),2009(4):148-149.

[8] 李言俊，张科.自适应控制理论及应用[M].西安：西北工业大学出版社,2005.

[9] 曾孟雄,赵千惠,欧阳文.基于PMSM的三环数控交流伺服系统[J].组合机床与自动化加工技术,2012(5):45-48.

[10] 赵晨，周洁敏，李小明． 基于永磁同步电机的 EMA 三闭环伺服控制系统[J].重庆理工大学学报(自然科学)，2016(3):104-111.

[11] 卜青.交流永磁同步电机伺服系统设计及仿真研究[D].武汉：华中科技大学,2007.

(责任编辑杨继森)

ResearchonServoPositioningSystemBasedonModelReferenceAdaptiveControl

YAN Shangxian, JIANG Xiaohui

(Ammunition Center, No.58 Research Institute of China Ordnance Industries, Mianyang 621000, China)

In view of the permanent magnet synchronous motor, the model reference adaptive control strategy is put forward to carry out the simulation study of servo positioning control. We establish a lyapunov function, and the design is composed of control object input and output of the model reference adaptive control law, and the control strategy can solve the uncertainty of the problems of nonlinear, time-varying system, and improve the position of the servo motor control performance. The simulation results show that the adaptive law can perform the task of positioning tracking with excellent performance, and the control effect is better.

permanent magnet synchronous motor; model reference adaptive control; servo positioning; Lyapunov stability theory; adaptive law

2017-04-12；

：2017-05-19

严尚贤(1990—)，男，硕士，主要从事自动控制系统设计研究。

10.11809/scbgxb2017.09.023

format:YAN Shangxian, JIANG Xiaohui.Research on Servo Positioning System Based on Model Reference Adaptive Control[J].Journal of Ordnance Equipment Engineering,2017(9):112-116.

TP273+.2

：A

2096-2304(2017)09-0112-05

本文引用格式：严尚贤，蒋晓辉.基于模型参考自适应控制的伺服定位系统研究[J].兵器装备工程学报，2017(9):112-116.