基于火星轨道器的着陆器定位误差及可观性分析

徐晴 彭玉明



基于火星轨道器的着陆器定位误差及可观性分析

徐晴1,2彭玉明1,2

（1 上海卫星工程研究所，上海 201109）（2 上海市深空探测技术重点实验室，上海201109）

针对深空探测过程中地面测控数传能力及着陆器星上功率受限等问题，文章提出了以轨道器为中继站的火星着陆器测量定位方法，旨在工程约束条件下分析地面测控站对着陆器的跟踪情况、轨道器与着陆器之间的可观性以及不同着陆点定位精度的差异，并给出相应的误差改善措施。该手段充分利用轨道器星上设备，达到提高定位精度的目的。结果表明，轨道器与着陆器之间通信的可见性要好于着陆器直接对地通信，有利于着陆器位置的确定；此外，通过几何因子和克劳美罗下限分析发现，若着陆器的着陆点位于轨道器星下点区域内，其定位精度较差。该方法充分利用轨道器与着陆器间的UHF通信链路，可为中国首次火星自主探测任务中着陆器的安全着陆提供参考。

火星探测 多普勒测速 最小二乘法 克劳美罗下限

0 引言

火星探测是国际深空探测领域的热点。我国首次自主火星探测任务于2016年初批复立项，该探测任务集“绕、落、巡”三步一体，具有开启月球以远深空探测里程碑的深远意义。

火星着陆器着陆于火表后，对地传输的方式有对地直接通信和器间间接通信两种。考虑到地火间距离远，火星表面存在大气衰减，探测器即使具备高增益天线对地通信能力，直接对地传输信息速率仍较低。以“火星探测漫游者”和“火星科学实验室”任务中所采用的多频制方案为例，采用10s时间完成1个状态遥测的传送，信息速率为0.8bit/s[1]；此外，地面站对着陆器的跟踪测量还存在火星遮挡及通信盲区等问题[2]。文献[2]分析了我国深空地面站对“火星探路者”号的跟踪及覆盖情况，结果表明跟踪时长为总时长的一半。美国的“好奇”号和“机遇”号探测器在进入、下降和着陆过程（Entry，descent and landing，EDL）以及最后着陆火表后的导航定位均依赖轨道器的中继测量。中继通信具备着陆器与轨道器通信距离短、轨道器直接对地通信能力强等优势[3]。NASA以往软着陆探测器的EDL过程中返向通信码速率可达到4~32kbit/s。未来由火星轨道器组成的中继网是辅以着陆器安全着陆定位的重要手段[4]；与地面GPS类似，轨道器与着陆器间的相对位置关系影响两者间的可观性，进而也影响着陆器的定位精度。

针对我国首次自主火星探测任务，本文提出了以轨道器为中继站，基于轨道器与着陆器间双程无线电测速测量的方式来获取着陆器位置的方案；对比器间通信与器地通信两者的可见性，并分析测量模型的可观性对定位精度的影响。该手段充分利用轨道器星上设备，在不增加额外成本的情况下提高设备利用率，提高着陆器定位精度。

1 着陆器测量模型

在我国火星探测的任务背景下，本文提出单个轨道器对着陆器的静态定位方法。轨道器与着陆器之间采用双程测速方式[5]，以高稳频率源为基准，收发信机在两器之间提供器间通信射频信道[6]。若轨道器接收机测得不同时刻频移量（也称观测量）为∆k，轨道器与着陆器的相对径向速度为kr，则火星固连坐标系下，频移与两器间相对径向速度的关系为

式中kr为轨道器与着陆器的相对径向速度；是kr在火星固连坐标系下的三个分量，可用待求的着陆器状态量L表示；0为轨道器发射信号的基频；为光速，忽略相对论效应。式（1）为表征观测量∆k与状态量L间非线性的观测方程，对其线性化得：

（2）

式中k为观测量与状态量的转移矩阵；,,为L在火星固连坐标系下的三个分量。给定着陆器位置估计初值，基于迭代最小二乘算法，利用一系列不同时刻轨道器接收机解调后的频移量迭代修正初值，最终得到着陆器的位置信息。

轨道器轨道参数的准确性是决定着陆器定位精度的重要因素。轨道测定主要通过地面站测距、测速以及测角获得[7]。无线电测距、测速可以直接获取轨道器相对于地面站的视向距离或视向速度，但对于垂直于视向的位置和速度不敏感[8]。由于轨道器与地面站的距离甚远，无线电信号微弱，测量精度受限且系统误差变大，以角度表示的测量精度也会越来越差。目前关于深空远距离探测器测角方式主要采用甚长基线干涉测量（Very Long Baseline Interferometry，VLBI）技术[9]，通过两个相距数千米的观测站同时跟踪轨道器信号，测量轨道器信号到达两站的时间差，进而得到轨道器位置矢量与基线的角度信息。目前我国主要的VLBI地面站有：北京、上海、昆明和乌鲁木齐。根据我国目前VLBI深空测控的能力以及工程约束条件[9]，本文给定轨道器在火星惯性坐标系下三个方向的位置误差为1km，三个方向的速度误差为1m/s。

2 着陆器对地通信及器间可见性

探测器发射升空后，测控通信系统是探测器与地球联系的唯一方式[10]。由于火星、地球以及太阳间的相对运动，火星的遮挡以及日凌都会对探测器的跟踪测量造成影响，使得探测器无法与地球实现全天候的连续通信[11]。

假定着陆器于2021年8月底开始科学任务，历时1个月，着陆点取在火星赤道平面内。首先考虑着陆器直接对地通信的情况，仍然选取前文中四个VLBI地面站对着陆器的通信情况进行分析，发现着陆器每个火星日平均对地可通信时间约6h，1个月内总的通信时长为205.84h。图1表征了地球、火星和太阳相对运动过程中，日–器–地夹角（Sun-Probe-Earth，SPE）和日–地–器夹角（Sun-Earth-Probe，SEP）的变化情况，当SEP和SPE均小于5°时，上下行链路无法正常通信，通过仿真得到：这1个月内的科学任务中，图1中最后1天SEP和SPE均存在小于5°的情况，造成约1.8h无法正常对地通信。

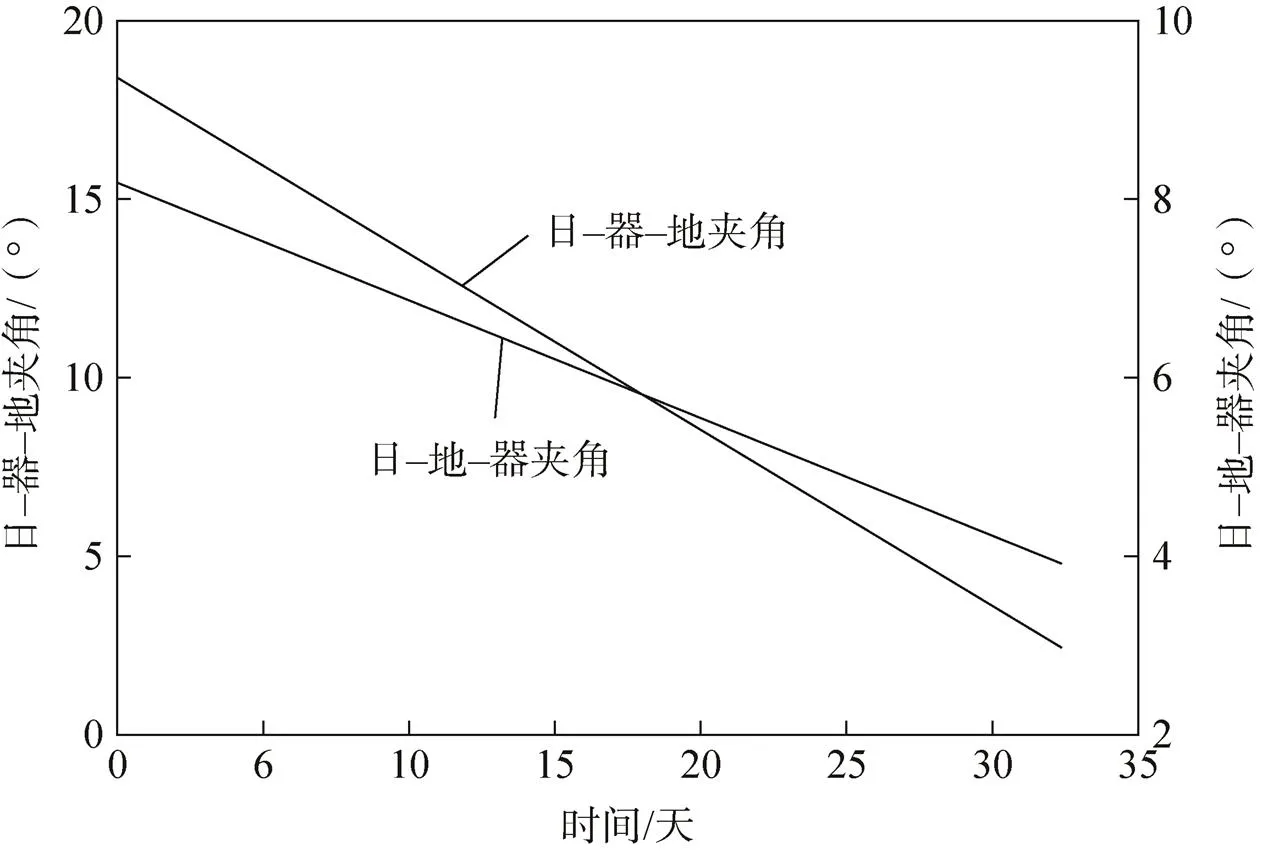
图1 日凌对着陆器直接通信的影响

以轨道器实现中继通信过程中，轨道器与着陆器的器间通信可见主要考虑到火星遮挡及天线仰角的限制[12]，着陆器的覆盖区是指以火星表面着陆点为中心的某一可观区，当轨道器的星下点位于可观区内，则轨道器相对于着陆器而言即为可观。可观区的大小与两器间的仰角有关，当仰角满足一定约束条件时，轨道器是可观的。着陆器观察轨道器的仰角是指：在含着陆器、火心和轨道器的平面内，轨道器视线方向与着陆器当地水平面之间的夹角。在平面内仰角可表示为

式中e为火星半径；为轨道器到火心距离；为着陆器位置矢量与轨道器位置矢量的夹角。

仍然考虑着陆器位于火星赤道面内的情况，选取仰角≥5°为约束条件，在MATLAB仿真中给出单圈内轨道器与着陆器满足通信弧段的时长占整个周期的比例。如图2所示，横坐标表示轨道器环绕圈数的序号，例如，（28,0.53）表示第28圈内轨道器与着陆器满足通信弧段的时长占整个周期的比例为53%。仿真发现：由于火星自转造成轨道器与着陆器间的相对运动，轨道器单轨内有的可通信弧段长，有的可通信弧段短，甚至有的环绕圈数内不存在可通信弧段。通过计算，着陆器科学任务1个月内器—器可通信总时长约217h，高于着陆器对地直接通信的时长。

图2 单圈内可通信弧段时长占整个轨道周期的比例

3 模型可观性分析

轨道器自身位置与速度误差确定后，轨道器与着陆器间的几何位置关系、轨道器对着陆器不同测量时刻的间隔弧段都会影响着陆器的定位精度，这与系统的可观性息息相关。可观性是指系统的状态能够由已有的量测数据唯一确定的能力，若系统不具备可观性，那么系统状态就不能被完全估计[13-14]。可观测度是对可观性的量化表述，下面针对本文的测速模型，引入几何因子和条件数两种量化方式来进行可观测度求解。

3.1 几何因子分析

几何因子能够定量地反映轨道器与着陆器间的几何位置对着陆器最终定位误差的影响情况，下面从多普勒测速模型入手简要说明。由着陆器测量模型可知，频移量与状态量间的关系为

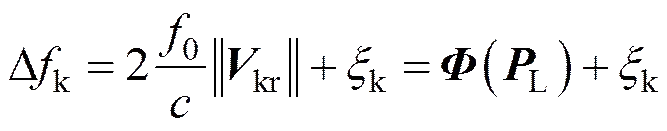
式中为赤经；为赤纬；表示求模。根据信息论的相关知识，克劳美罗下限（Cramer-Rao Low Bound，CRLB）可作为反映某点的定位误差协方差阵的参数，固连坐标系下着陆器在某个着陆点的CRLB为

（6）

式中c即为式（6）右边矩阵对角线上的元素。

3.2 条件数分析

轨道器对着陆器不同测量时刻的间隔弧段也会影响着陆器的定位精度，这里采用条件数进行描述。条件数反映了系统解随观测数据中误差变化的敏感程度，是系统本质、内部结构特性的反映[16]。对于线性系统=而言，当状态存在微小扰动时，由矩阵扰动理论可知

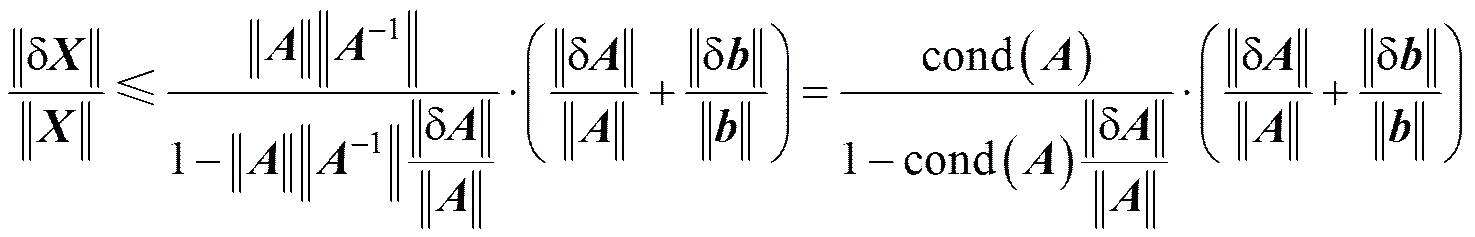
式中为本文测量模型的观测量，相当于章节1中的∆k；为观测量与状态量间的转移矩阵，相当于章节1中的k；为状态量，用待求的着陆器的位置量表示；d和d是方程左右两边的扰动项；d是由此引起的的扰动项。将Cond()定义为条件数，即反映外界扰动对系统解精度影响的上界。Cond()越小，状态的微小扰动对最终解算精度影响越小，解的可靠性越高。由矩阵范数可知，选取合适的系统参数使条件数接近1，系统对外界扰动误差变化的敏感度越不明显。

不考虑外界误差源的影响，着陆器的位置由轨道器经过三次多普勒测速即可解算，即

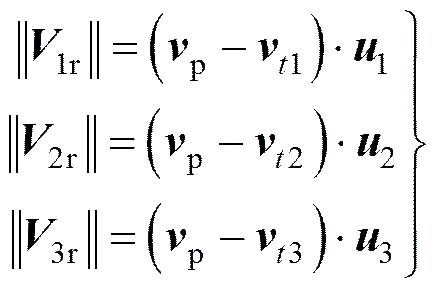
式中1r,2r,3r为三次测量时轨道器与着陆器的相对径向速度；p为固连坐标系下着陆器的速度矢量；1,2,3为三次测量时轨道器的速度矢量；1,2,3分别为三次不同时刻着陆器与轨道器间视线单位矢量。将这些矢量在固连坐标系下各自的分量代入展开后可得：

（10）

将式（10）转换为如下表达式

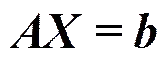
式中，和分别为：。

根据条件数Cond()的相关理论应使量测方程的Cond()达到最小，从而获得不同测量点的间隔弧段。

4 仿真条件及分析

为验证本文提出的基于单个轨道器的双程测速模型以及该模型可观性分析手段的可行性，下面给出仿真实例。仿真过程中轨道器位置参数由地面确定，着陆器标称位置假定在赤道上，以火心赤纬和火心赤经表示。本文采用双程测速方式，信号基频取400MHz，转发比为1，多普勒测量准确度取10mHz。仿真过程中着陆器的定位精度受到轨道器位置参数误差、收发信机的基频误差、传播过程中的大气频偏误差[17]、火星引力场模型的不确定性以及宇宙背景辐射等影响，本文考虑前三个主要误差源。

4.1 多轨测量精度分析

轨道器单轨测量时，由于可见弧段较短，测量的数据量少且有效性较低，为提高着陆器的定位精度，考虑利用轨道器多轨测量的信息共同解算。图3给出了2轨、4轨情况下着陆器定位精度的情况。由仿真结果发现：以每2轨测量得到的数据进行仿真，着陆器的位置误差在10km以内；以每4轨测量数据仿真时，着陆器位置误差可以缩减到4km左右。

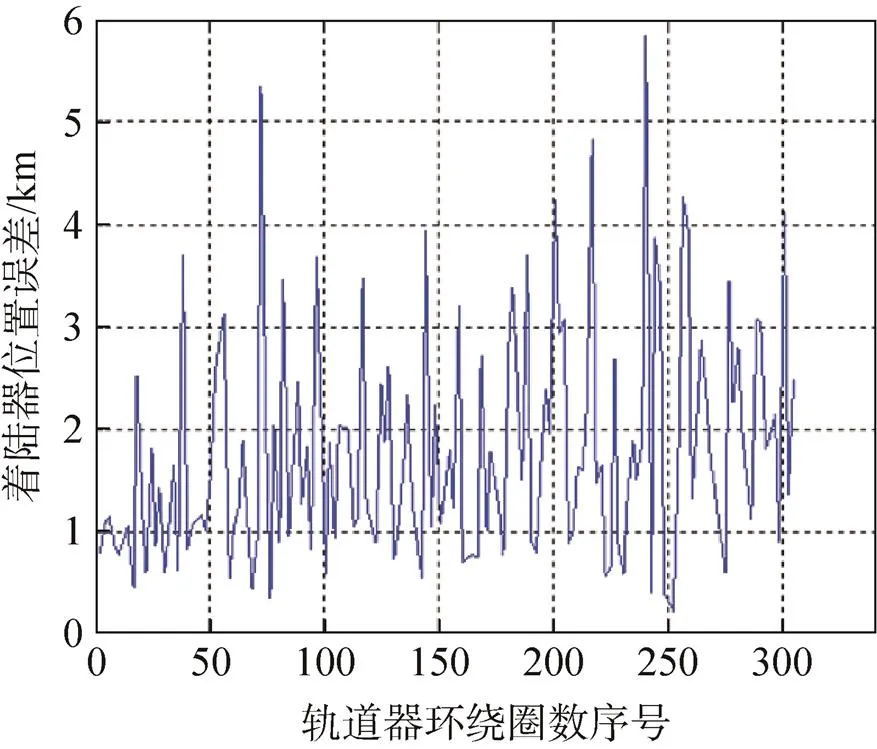
（a）2轨测量 （b）4轨测量

4.2 几何因子和条件数分析

（1）几何因子分析

根据3.1节关于几何因子的阐述，轨道器与着陆器的相对位置也是影响着陆器最终定位的关键因素。在火星表面采用网格化搜索方式，选取不同的着陆点位置坐标，经度变化范围为–180º~180º，纬度变化范围为–90º~90º，同时考虑轨道器星下点轨迹的覆盖情况，得到图4中关于火星表面不同着陆点的GDOP分布和定位误差值。

（a）几何因子分布等高线图 （b）轨道器星下点轨迹（1圈）

（a）Contour map of GDOP （b）Substral point of orbiter (1 circle)

（c）不同着陆位置的误差大小 （d）轨道器星下点轨迹（7圈）

由仿真结果可知：图4（a）中等高线图的红色部分表示数值大，与图4（b）对比发现轨道器星下点附近的GDOP要高于远离星下点轨迹的区域；图4（c）误差大小的仿真结果是在考虑了器间通信弧段约束、不同误差源影响以及多圈测量情况下得到的，且图4（c）的误差分布情况与图4（d）的多圈星下点轨迹一致，表明当着陆器的标称位置取在星下点附近区域时，着陆器的定位精度比较差。这是由于当轨道器经过着陆器天顶时，轨道器与着陆器的相对径向速度变化小，测量数据的有效性低，因此导致误差较大。

（2）条件数分析

不考虑外界误差的影响，理论上轨道器只需对着陆器进行三次测量就能获得着陆器的位置坐标，但不同测量时刻的间隔时间仍会对定位精度造成影响[18-20]。根据条件数Cond()的相关理论，应使量测方程的Cond()达到最小，条件约束为轨道器与着陆器三次的视线方向都是单位矢量，即：

仿真计算发现：当轨道器对着陆器三次测量时三次视线方向满足两两正交的条件，系统误差和过程测量误差对最后的定位精度影响最小，1,2,3两两视线方向之间的夹角计算结果均为1.57rad。实际测量过程中考虑到轨道器与着陆器间的可见弧段有限，未必存在两两正交的情况，此时要求三个矢量间的夹角尽可能地接近90º。

5 结论

以轨道器为中继站的火星着陆器测量定位，旨在分析轨道器轨道类型以及环绕圈数对着陆器最终定位精度的影响。结果表明，若采用2轨环绕测量，着陆器定位精度提高到10km以内；若圈数继续增加，定位精度继续提高。轨道器与着陆器的相对位置也是影响最终定位的重要因素。通过几何因子和克劳美罗下限分析发现若着陆器的着陆点位于轨道器星下点区域内，其定位精度较差。该手段充分利用轨道器星上设备提供辅助信息，增加地面对着陆器跟踪测量的手段。

[1] 刘适, 黄晓峰, 乔旭君. 火星探测进入、下降、着陆过程通信方案[J]. 航天器工程, 2015, 24(4): 94-101. LIU Shi, HUANG Xiaofeng, QIAO Xujun. Telecommunication System Scheme for Mars Probe during EDL[J]. Spacecraft Engineering, 2015, 24(4): 94-101. (in Chinese)

[2] 严韦, 魏二虎, 平劲松, 等. 我国火星探测器遥控跟踪网效率分析[J]. 测绘通报, 2009, 1(4): 16-18. YAN Wei, WEI Erhu, PING Jinsong, et al. Efficiency Analysis of China’s Mars Detector Remote Control Tracking Network[J]. Bulletin of Surveying and Mapping, 2009, 1(4): 16-18. (in Chinese)

[3] EDWARDS C D. Relay Communications for Mars Exploration[J]. International Journal of Satellite Communications & Network, 2007, 25(2): 111-145.

[4] 彭玉明. 新型火星EDL导航、制导与控制技术研究[D]. 南京: 南京航空航天大学, 2011. PENG Yuming. New Research on Mars EDL Guidance, Navigation and Control Technology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011. (in Chinese)

[5] 潘理刚, 李宏圆. 基于WGS-84椭球地球模型的单星多普勒测频定位技术[J]. 舰船电子对抗, 2013, 36(6): 17-21. PAN Ligang, LI Hongyuan. Single Satellite Doppler Frequency Measurement and Location Technology Based on WGS-84 Ellipsoid Earth Model[J]. Shipboard Electronic Countermeasure, 2013, 36(6): 17-21. (in Chinese)

[6] 陆启省, 南树军, 白沁园. 基于单星定位的火星着陆器初定位方法研究[J]. 航天器返回与遥感, 2012, 33(6): 10-16. LU Qisheng, NAN Shujun, BAI Qinyuan. Initial Location Method for Mars Lander Based on Single Satellite Location[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(6): 10-16. (in Chinese)

[7] TAPLEY B, SCHUTZ B, BORN G. Statistical Orbit Determination[M]. London: Elsevier, 2004.

[8] 李金岭, 乔书波, 刘鹏. 基于我国VLBI网航天器定位归算仿真分析[J]. 宇航学报, 2011, 33(11): 2333-2338. LI Jinling, QIAO Shubo, LIU Peng. Simulation Analysis of Positioning Reduction of Spacecraft as per the Chinese VLBI Network[J]. Journal of Astronautics, 2011, 33(11): 2333-2338. (in Chinese)

[9] LIU Qinghui, CHEN Ming, GOOSSENS S. Applications of Same-beam VLBI in the Orbit Determination of Multi-spacecrafts in a Lunar Sample-return Mission[J]. Science China Physics, Mechanics & Astronomy, 2010, 53(6): 1153-1161.

[10] 曹建峰, 黄勇, 胡小工. 利用中国VLBI网实现对“火星快车”的测定轨[J]科学通报, 2010, 55(27-28): 2659-2666. CAO Jianfeng, HUANG Yong, HU Xiaogong. Determination of the Orbit of Mars Express Based on China VLBI Net[J]. Chinese Science Bulletin, 2010, 55(27-28): 2659-2666. (in Chinese)

[11] 邸凯昌. 勇气号和机遇号火星车定位方法评述[J]. 航天器工程, 2009, 18(5): 1-5. DI Kaichang. Positioning Methods Review of Curiosity and Opportunity Mars Rovers[J]. Spacecraft Engineering, 2009, 18(5): 1-5. (in Chinese)

[12] 饶启龙. 基于CCSDS的火星探测器测控通信系统链路分析与设计[D]. 上海: 上海交通大学, 2012. RAO Qilong. The Link Analyzation and Design Based on CCSDS for Mars Probe TTC &System[D]. Shanghai: Shanghai Jiao Tong University, 2012. (in Chinese)

[13] 章仁为.卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998: 8. ZHANG Renwei. Satellite Orbit Attitude Dynamics and Control[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1998: 8. (in Chinese)

[14] 史忠科. 最优估计的计算方法[M]. 北京: 科学出版社, 2001: 5. SHI Zhongke. Calculation Method of Optimal Estimation[M]. Beijing: Science Press, 2001: 5. (in Chinese)

[15] 黄翔宇, 崔平远, 崔祜涛. 深空自主导航系统的可观性分析[J]. 宇航学报, 2006, 27(3): 332-338. HUANG Xiangyu, CUI Pingyuan, CUI Hutao. Observability Analysis of Deep Space Autonomous Navigation System[J]. Journal of Astronautics, 2006, 27(3): 332-338. (in Chinese)

[16] 徐义. 基于多普勒信息的单星无源定位新技术研究[D]. 长沙: 国防科学技术大学, 2009. XU Yi. Research on New Passive Location of Single Satellite Based on Doppler Information[D]. Changsha: National University of Defense Technology, 2009. (in Chinese)

[17] LEVANON N. Quick Position Determination Using 1 or 2 LEO Satellites[J]. IEEE Transactions on Aerospace and Electronic Sysytems, 1998, 34(3): 736-754.

[18] 王萌, 马冠一, 马利华. 卫星定位误差椭球的几何特征研究[J]. 宇航学报, 2012, 33(11): 1593-1600. (in Chinese) WANG Meng, MA Guanyi, MA Lihua. A Study on Geometric Feature of Error Ellipsoid in Satellite Positioning Systems[J]. Journal of Astronautics, 2012, 33(11): 1593-1600. (in Chinese)

[19] 吴勃英. 数值分析原理[M]. 北京: 科学出版社, 2012: 1. WU Boying. Numerical Analysis Principle[M]. Beijing: Science Press, 2012: 1. (in Chinese)

[20] 朱圣英, 常晓华, 崔祜涛. 基于视线矢量的深空自主导航算法研究[J]. 空间科学学报, 2011, 31(4): 534-540. ZHU Shengying, CHANG Xiaohua, CUI Hutao. Research on Deep Space Autonomous Navigation Algorithm Based on Line of Sight Vector[J]. Chinese Journal of Space Science, 2011, 31(4): 534-540. (in Chinese)

（编辑：夏淑密）

Error and Observability Analysis for Mars Lander Positioning Based on Orbiter Measurement

XU Qing1,2PENG Yuming1,2

（1 Shanghai Institute of Satellite Engineering, Shanghai 201109, China）（2 Shanghai Key Laboratory of Deep Space Exploration Technology, Shanghai 201109, China）

Aiming at the challenges of deep space limited telemetry capability of telemetry, tracking and command (TT&C) stations and restricted power of lander, a novel two-way doppler range rate measurement based on relay orbiter is presented in this paper. This research aims to analyze tracking condition of lander from ground TT&C stations and consider observability between two probes. Position precisions of different landing sites are revealed. This paper finally provides several solutions to improve lander’s precision. This method takes advantage of orbiter’s communication devices to increase position precision efficiently. The results indicate that observability of orbiter-lander communication is better than lander’s direct communication to earth, which is beneficial for lander’s position determination. By analysis of geometric dilution of precision and Cramer-Rao lower bound, when landing site is within the area of orbiter ground track, position precision will get worse. This method takes good use of ultra-high frequency (UHF) link between orbiter and lander and these conclusions could provide valuable references for lander’s safe landing of China’s first independent Mars exploration program.

Mars exploration; doppler range rate measurement; least square method; Cramer-Rao lower bound

V448

A

1009-8518(2017)04-0018-09

10.3969/j.issn.1009-8518.2017.04.003

徐晴，女，1992年生，2017年获上海航天技术研究院硕士学位。研究方向为深空探测器总体技术。E-mail: qqqw2012@ 126.com。

彭玉明，男，1984年生，2011年获南京航空航天大学硕士学位。研究方向为深空探测器制导、导航与控制技术。

2017-04-16

国家重点基础研究发展计划（973计划）项目（2014CB744200）