一种基于星表特征直线匹配的着陆器位姿估计算法

邵巍，顾天昊

（青岛科技大学 自动化与电子工程学院，青岛 266042）

一种基于星表特征直线匹配的着陆器位姿估计算法

邵巍，顾天昊

（青岛科技大学 自动化与电子工程学院，青岛 266042）

针对深空探测星际着陆过程中的自主导航问题，提出一种基于星表特征直线的着陆器位姿估计算法。该算法首先采用EDLine算法对着陆过程中所拍摄的图像进行特征直线提取；其次根据直线局部特征对特征直线进行匹配；之后利用至少3对已匹配的特征直线，建立关于着陆器位姿的几何约束方程；然后根据奇异值分解法得到着陆器位姿的候选解；最终通过最小二乘法从候选解中选取着陆器位置、姿态的唯一解。仿真结果表明：该算法可以快速估计着陆器位姿，且在高度为2 000 m时位置误差小于2 m、姿态误差小于0.10°。

特征直线匹配；视觉导航；深空探测；直线描述符；星际着陆

0 引 言

随着深空探测技术的不断发展，着陆段自主导航已经成为现阶段的研究热点。由于传统惯性导航方法存在误差积累以及初始误差难以修正的问题，难以实现精确着陆的目标。近年来，视觉导航方法由于其自身的可靠性、廉价性、自主性[1]成为世界各国航天领域专家研究的热点并取得了大量成果[2-5]。

2004年美国喷气推进实验室（Jet Propulsion Laboratory，JPL）设计的下降图像运动估计系统（DIMES）首次利用对Harris角点的检测和匹配进行着陆器的水平速度的估计[6]，并应用于“机遇号”“勇气号”，但该系统匹配算法稳定性较差，并在估计水平速度过程中丢失了一对匹配点。同时，其它基于特征点匹配的导航算法也被不断发展创新[7]。Ma等[8]在以特征点为导航路标的基础上利用移动最小二乘的方法获得着陆器姿态。然而以特征点作为导航路标存在两方面缺点：①一般图像中可提取的特征点数量较多，在提取和匹配的过程中计算量大且复杂、内存使用率高；②一般情况下，特征点的全局位置信息未知，导致基于特征点匹配的算法只能用于估计着陆器相对于上一时刻的位姿。陨石坑作为另一类导航路标，可利用其已知的地理位置坐标，对着陆器绝对位姿进行估计[9-10]。然而星表陨石坑分布不均，在无陨石坑的星表区域基于陨石坑匹配的算法不能适用，例如NASA为“火星2020”任务拟定的3个着陆点（如图 1～3所示区域）以及“好奇号”着陆区域（如图 5所示区域）均不适合利用陨石坑为导航路标；同时陨石坑的提取与匹配算法较为困难、利用现有的匹配算法[11-12]，容易出现误匹配的情况。星表的山脊、沟壑和其他近似直线的纹理特征，比陨石坑分布更为广泛。这些特征地理坐标可提前获取，因此可作为绝对导航路标。本文针对着陆段导航，提出一种利用星表特征直线作为导航路标的着陆器位姿估计算法，该算法从着陆图像中提取出星表特征直线，与星表基准直线特征数据库（提前建立）匹配3对以上特征直线，可计算出着陆器的位置和姿态。

图1 NASA“火星2020”任务候选着陆地点IFig.1 The first landing site workshop for the Mars 2020 rover mission

图2 NASA“火星2020”任务候选着陆地点IIFig.2 The second landing site workshop for the Mars 2020 rover mission

图3 NASA“火星2020”任务候选着陆地点IIIFig.3 The third landing site workshop for the Mars 2020 rover mission

1 特征直线的检测与匹配

本文采用Cuneyt Akinlar等[13]提出的EDline算法对图像中的特征直线进行提取。该算法首先对图像进行高斯滤波处理；其次计算图像上每个像素的梯度值以及方向；然后将近似边缘的像素组成多个锚点，并将各锚点相互连接得到边缘提取结果；最后运用最小二乘法，将拟合误差在阈值内的序列像素拟合为直线，得到直线的提取结果。该算法与以往算法相比，边缘提取结果连续、整齐，提取运算速度大大提升。

针对已提取的特征直线，本文利用Zhang等[14]提出的直线匹配算法，该算法利用直线描述符对直线的局部特征进行描述，并根据直线的局部特征得到候选匹配对，最终通过对候选匹配对建立权重关系图得到正确匹配对。该算法相对已有算法，其对经过旋转、缩放的图像更具有鲁棒性，并且使用直线描述符会提升计算速度。

从图 4～5可以看出，星表特征直线的提取与匹配结果基本正确，为基于特征直线匹配的着陆器位姿估计算法那奠定了基础。

图4 根据“勇气号”火星探测器所拍摄的图像进行特征直线提取与匹配效果图Fig.4 Lines extraction and matching based on the image taken by “Spirit”

图5 根据“好奇号”火星探测器所拍摄的图像进行特征直线提取与匹配效果图Fig.5 Lines extraction and matching based on the image taken by“Curiosity”

2 几何约束及位姿估计

2.1 基于平面特征直线位姿估计几何约束

图6 坐标系示意图Fig.6 The geometry diagram map of coordinate systems

将直线Li的单位方向向量在世界坐标系下记作，将位于世界坐标系的方向向量，转化成位于局部坐标系的方向向量的旋转矩阵记作。由于所在方向作为局部坐标系的轴，所以

由于L0位于平面上，则方向向量V0与该平面法线n0垂直。因此，将相机坐标系转换成局部坐标系的旋转矩阵满足。同时可参数化为其中，任意矩阵的第二列元素为n0，表示围绕轴旋转α角的旋转矩阵，表示围绕Ym轴旋转β角的旋转矩阵。因此，从相机坐标系转化成世界坐标系的旋转矩阵为

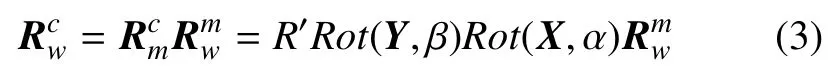
只需将α与β求出，即可得到。

现在，选取投影长度第二的参考线L1作为求解过程的辅助线，由于

可整理为

因此可得到P3L多项式

2.2 位姿估计

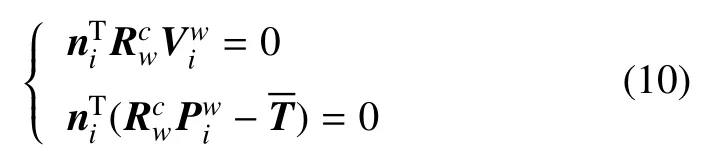
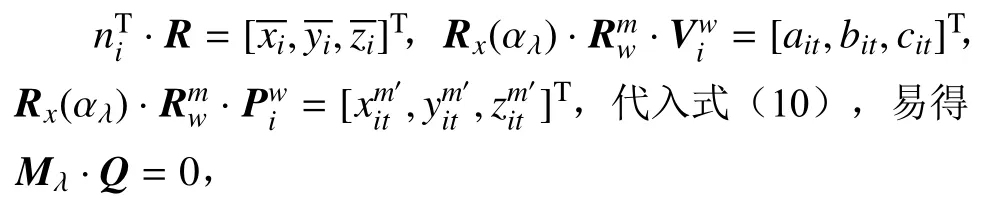
其中

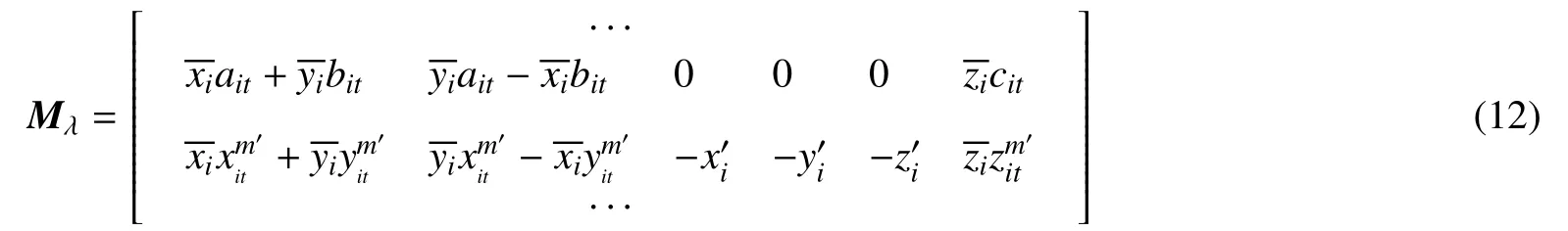
利用平面直线的导航算法求得位姿参数的多个解，因此需要从这些解中选取出精确度最高的位姿参数。为了消除噪声干扰，应在确定最优解之前，先对位姿参数进行二次校正[15]。

首先在直线Li上任一点，并选取离世界坐标系原点最低记作，则有

然后，计算世界坐标系下点的坐标值和相机坐标系下点坐标值的相关性

其中

最后，对校正后的候选解进行最优解的选取。利用位姿参数误差表达式

将误差大于1 0-4的旋转矩阵去除。再利用选出误差最小的位姿参数解。对于所得解，可进一步反复校正[16]，直到误差收敛到符合导航精确度的值。

3 实验仿真及结果分析

本文仿真实验利用3个不同变量与误差的关系来检验本文算法的鲁棒性和精确性。

首先，由于该算法是以平面直线为基础所推导，因此需要检测地面起伏高度与位姿误差的关系。将地面起伏高度作为该算法仿真唯一变量，并使其从10 m逐步变化到100 m。其他参数如表 1所示，其中直线端点噪声强度为对像平面投影直线；li的端点的坐标加入高斯白噪声强度。在不同地面起伏高度下，分别独立实验1 000次，并根据准则剔除1 000次仿真实验中的粗大误差。

表1 仿真参数Table 1 Representative parameters of the simulation

根据上述仿真参数进行实验，着陆器的姿态与位置误差与地面起伏高度的关系如图 7～8所示。着陆器的位姿误差随着地面起伏高度的上升而增大。在地面起伏高度100 m以内的情况下误差变化趋势稳定，姿态误差始终小于0.5°，位置误差始终小于10 m。由于着陆高度为2 000 m，地面起伏高度与着陆高度相比较为微小，因此地面起伏高度对算法影响较小。

图7 姿态误差与地面起伏高度关系图Fig.7 The relationships between the lander’s attitude and the depth of surface

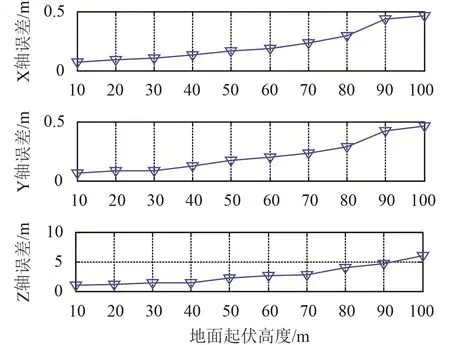
图8 位置误差与地面起伏高度关系图Fig.8 The relationships between the lander’s position and the depth of surface

图9 姿态误差与直线数量关系图Fig.9 The relationships between the lander’s attitude and the number of matched feature lines

图10 位置误差与直线数量关系图Fig.10 The relationships between the lander’s position and the number of matched feature lines

其次，测试匹配直线数量与位姿误差的关系。此仿真以匹配直线数量为唯一变量，令匹配直线数量从4对开始递增到14对。其他参数如表 1所示，在匹配直线数量不同的条件下，分别独立实验1 000次，并根据准则剔除1 000次仿真实验中的粗大误差。

从图 9～10可以看出，着陆器的位姿误差随着特征直线数量的增加而减小。当直线数量超过10条时，姿态误差可以控制在0.1°以内，位置误差小于1 m。这是因为随着特征直线数量的增加，P3L多项式个数增加，几何约束增强，位姿估计更加精确。

最后，检测着陆高度与位姿误差的关系。假设着陆器从4 000 m开始逐步下降直至500 m，其他参数如表 1所示。着陆器的位姿与下降高度的关系，如图 11～12所示。

从图 11~12可以看出，随着高度的降低，着陆器的位置误差逐渐减小，这是因为随着高度的降低，特征直线在像平面所成的投影逐渐变长，噪声的影响逐渐减小，从而使得位置精度提升。在本文的仿真条件下，若特征直线匹配数量在10条时，着陆器位置误差可以控制在2 m以内，姿态误差控制在0.1°以内。

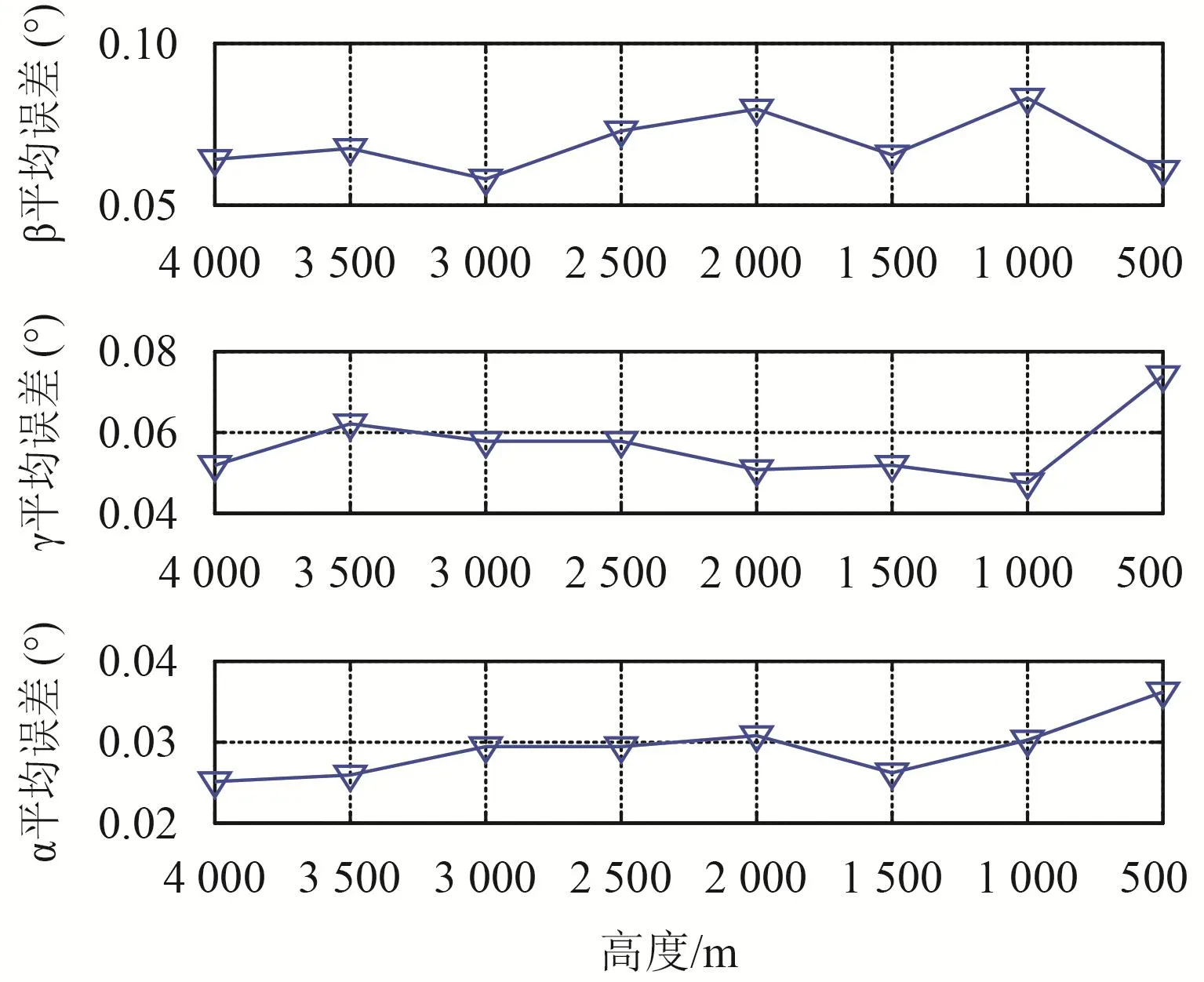
图11 姿态误差与着陆高度关系图Fig.11 The relationships between the lander’s attitude and the height of lander

图12 位置误差与着陆高度关系图Fig.12 The relationships between the lander’s position and the height of lander

4 结 论

本文提出一种利用星表特征直线来估计着陆器位姿的算法，推导了利用三条以上的特征直线以及其对应的像平面直线，计算出着陆器位姿的唯一解的过程，并且通过仿真实验表明了这种方法的可行性。但该算法并未加入滤波算法，可通过滤波算法对该算法所得到的位姿参数进一步估计。同时，利用星表特征直线来估计着陆器位姿也存在一定的局限性，因为需要知道已匹配特征直线的地理位置信息才能计算出着陆器的绝对位姿。对于此情况，可以进一步研究在特征直线的绝对位置坐标未知时，利用相邻帧间图像的特征直线匹配来估计着陆器的相对位置、姿态。

[1]黄显林，姜肖楠，卢鸿谦，等.自主视觉导航方法综述[J].吉林大学学报：信息科学版，2010，28（2）：158-165.Huang X L，Jiang X N，Lu H Q，et al.Survey of vision for autonomous navigation [J].Journal of Jilin University：Information Science Edition，2010，28（2）：158-165.

[2]Wokes D，Wokes S.Surveying and pose estimation of a lander using approximative crater modelling[C]//AIAA Guidance，Navigation，and Control Conference.Canada：AIAA，2010.

[3]Simard Bilodeau V，Neveu D，Bruneau-Dbuc S，et al.Pinpoint lunar landing navigation using crater detection and matching：design and laboratory validation[C]//AIAA Guidance，Navigation，and Control Conference.Minneapolis：AIAA，2012.

[4]Li S，Cui P Y，Cui H T.Autonomous navigation and guidance for landing on asteroids [J].Aerospace Science and Technology，2006，54（10）：763-771.

[5]高锡珍，邵巍，冷君阁，等.一种基于陨石坑拟合椭圆的着陆器位姿估计算法[J].深空探测学报，2015，2（3）：241-245.Gao X Z，Shao W，Leng J G，et al.An attitude and position determination algorithm of lander based on craters for precision landing[J].Journal of Deep Space Exploration，2015，2（3），241-245.

[6]Cheng Y，Goguen J，Johnson A，et al.The Mars exploration rovers descent image motion estimation system[J].IEEE Intelligent Systems，2004，19（3）：13-21.

[7]Jie M，Huang X，Yin H，Lu H.A precise vision-based navigation method for autonomous soft landing of Lunar explorer [C]//2007 IEEE International Conference on Robotics and Biomimetics （ROBIO）.Sanya：IEEE，2007.

[8]Ma H，Xu S.Only feature point line-of-sight relative navigation in asteroid exploration descent stage[J].Aerospace Science and Technology，2014，39：628-638.

[9]Lu T，Hu W，Liu C，et al.Relative pose estimation of a lander using crater detection and matching[J].Optical Engineering，2016，55（2）：102-112.

[10]Shao W，Gao X，Xi S，et al.Attitude and position determination based on craters for precision landing[J].Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2016，230（10）：1934 -1942.

[11]Cheng Y，Ansar A.A landmark based position estimation for pinpoint landing on mars[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation.Spain：IEEE，2005.

[12]Yu M，Cui H，Tian Y.A new approach based on crater detection and matching for visual navigation in planetary landing[J].Advances in Space Research，2014，53 （12）：1810-1821.

[13]Akinlar C，Topal C.EDLines：a real-time line segment detector with a false detection control[J].Pattern Recognition Letters，2011，32（13）：1633-1642.

[14]Zhang L.Line primitives and their applications in geometric computer vision[D].German：Department of Computer Science，Univ.，Multimedia Information Processing Group，2013.

[15]Umeyama S.Least-squares estimation of transformation parameters between two point patterns[J].IEEE Transactions on pattern analysis and machine intelligence，1991，13（4）：376-380.

[16]Kumar R，Hanson A R.Robust methods for estimating pose and a sensitivity analysis[J].CVGIP：Image Understanding，1994，60（3）：313-342.

A New Approach Based on Line Correspondences for Attitude and Position Estimation of Lander

SHAO Wei，GU Tianhao
（College of Automation & Electronic Engineering，Qingdao University of Science and Technology，Qingdao 266042，China）

In order to achieve precise pin-point landing in deep space exploration missions，a new approach is presented to estimate accurately the lander’s attitude and position based on line correspondences during descent phase.Firstly，lines on the images taken by onboard navigation camera are detected and matched in this algorithm.The linear equations are deduced bynlines and their projection lines.Then，according to the Singular Value Decomposition，the candidate solutions are computed.Lastly，the unique solution about the attitude and position of the lander is obtained by using the least square method.The extensive experiments demonstrate that the error of attitude is less than 0.1° and the error of position is less than 2 m.

attitude and position estimation；line correspondences；visual navigation；deep space exploration mission；line band

V41

A

2095-7777（2017）03-0281-06

[责任编辑：杨晓燕，英文审校：朱鲁青]

10.15982/j.issn.2095-7717.2017.03.013

邵巍，顾天昊.一种基于星表特征直线匹配的着陆器位姿估计算法[J].深空探测学报，2017，4（3）：281-286.

Reference format：Shao W，Gu T H.A new approach based on line correspondences for attitude and position estimation of lander[J].Journal of Deep Space Exploration，2017，4（3）：281-286.

2017-04-15

2017-05-31

顾天昊（1990- ），男，硕士研究生，主要研究方向：深空探测自主导航。

通讯地址：青岛市郑州路53号青岛科技大学自动化与电子工程学院（266042）。

电话：15863118690

E-mail：gth901007@163.com