基于动态罚函数的火星探测器多学科协同优化
2017-09-27柳明星张伟张恒刘华清
柳明星,张伟,张恒,刘华清
(1.上海卫星工程研究所,上海 201109;2.上海市深空探测技术重点实验室,上海 201109)
基于动态罚函数的火星探测器多学科协同优化
柳明星1,2,张伟1,2,张恒1,2,刘华清1
(1.上海卫星工程研究所,上海 201109;2.上海市深空探测技术重点实验室,上海 201109)
针对火星探测器飞行距离遥远和飞行环境复杂带来总体设计参数难以优化的问题,建立以遥感性能和总重为综合优化目标的优化模型,考虑探测器的轨道、载荷、电源等分学科,基于协同优化方法建立火星探测器的系统级和学科级优化函数,采用自适应动态罚函数加快优化的收敛速度,最终获得协同一致的优化结果。仿真结果表明:协同优化方法应用于火星探测器总体参数优化的可行性和有效性,可为探测器的总体设计提供技术参考。
火星探测器;总体设计;建模;协同优化;动态罚函数
0 引 言
航天器总体设计是一个多学科交叉融合,需要花费较长时间协调和权衡的过程。当前,设计者主要根据经验进行设计,经过反复的人工迭代最终得到一个满足任务要求的方案,这种设计方法往往很难保证系统的最优性,而且周期长、成本高。
现代的数字化设计方法注重引入优化的思想来提高总体设计水平,特别是在近地卫星的总体参数优化中已经有了相当多的研究成果。Wu等[1]尝试将优化方法引入卫星设计,对多种优化算法进行了比较。文献[2]针对航天器对地观测调度中资源约束发生突变的情况,提出了一种基于蚁群算法的启发式重调度算法,可有效提高卫星观测任务自主调度中的数据收集能力和应用水平。文献[3]针对复杂系统设计提出了协同优化方法,可为卫星总体设计问题的优化提供有效的支持。文献[4]~[6]运用多学科优化的方法实现了对对地观测卫星的总体优化。文献[7]和文献[8]将MDO方法应用到小卫星的参数优化设计中,大大提升了设计效率;文献[9]对月球基地的多学科优化进行了研究,旨在寻找优良的基地材料组成,对其优化所涉及的热、结构、空间辐射、材料属性等学科进行了分析,采用遗传算法实现了月球基地的优化。然而在深空探测器的总体优化设计中尚未得到深入研究,随着我国火星探测任务的逐步实施,有必要开展深空探测器的总体设计优化方法研究。协同优化是目前一种较好的优化方法,在多学科耦合复杂系统的优化中有其独到的优势。
本文从探测器设计的工程需求出发,以火星探测器环绕火星进行遥感为工程背景,考虑探测器的轨道、载荷、电源等学科,建立火星探测器的协同优化模型,基于动态罚函数的方法对一致性约束进行处理以加快收敛速度,最终得到协同一致的优化结果。
1 协同优化方法
协同优化的思想是将一个优化问题分为系统层与学科层。学科层与学科层之间保持着相对独立性,学科层之间不进行数据交互,而是通过与系统级之间的一致性约束信息进行信息交互,从而实现学科之间的参数解耦。系统层优化后将系统层的优化值向下传递给学科层,而各个学科层也将其优化后的优化值向上反馈给系统层。系统层优化的目标函数为原始的系统目标函数,约束函数J是由各个学科优化问题最优解构成的集合,它用来解决学科之间以及学科与系统之间状态变量的不一致性。在学科层,优化变量为本学科的状态变量,通过与系统层传递下来的耦合变量作差并平方构成学科层的最小化优化目标函数Ji。
协同优化的特点在于引入了一致性约束J,J在优化迭代过程中收敛趋近于0,由于J的构造是系统层和学科层耦合变量的平方差形式,当J逐步趋近于0时,各个学科之间以及学科与系统之间耦合变量也就趋于统一,这就是协同优化解决参数耦合的关键,通过一致性约束J协调了各个学科层的耦合关系。假设系统可以分为N个子学科,则协同优化的数学形式如图 1所示。
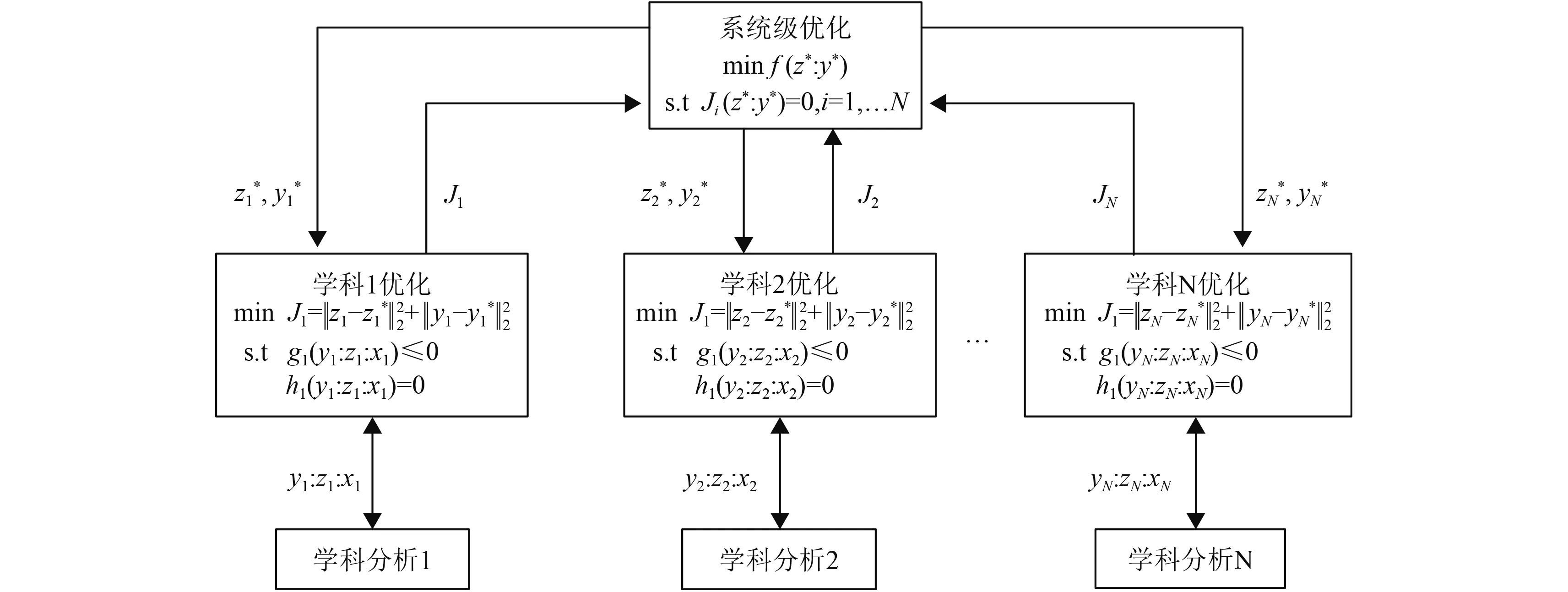
图1 协同优化计算框架Fig.1 The framework of collaborative optimization
2 动态罚函数处理约束
对于系统级一致性约束Ji的处理,可通过罚函数法将其加权到系统的目标函数中,通过惩罚项的作用迫使优化结果向满足一致性约束的方向靠近[9-10],即系统级优化目标转化为
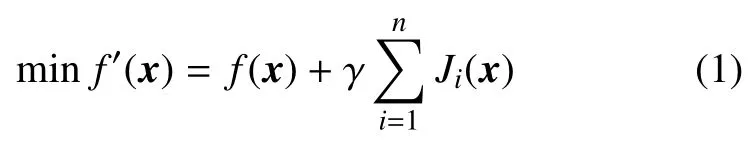
利用罚函数处理约束问题时,其性能很大程度上取决于罚因子的选择。在优化过程中可利用一致性约束信息构造动态自适应罚因子表达式为

其中:b,m和α是常数;k为一致性约束信息。
当k非常小时,的值主要取决于常数项b,该值使得此时目标函数的值仍然受一致性约束信息限制,增强了协同优化的稳定性。一致性约束信息为
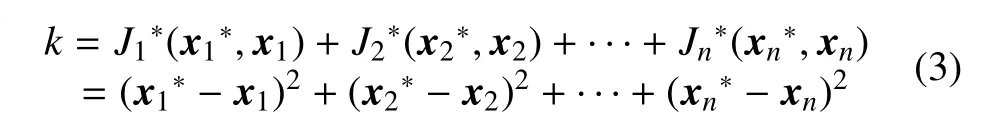
在迭代过程中,上一次优化的一致性约束信息k越大,说明系统层与子问题层的优化结果差异越大,此时罚因子γ的值随着k值而增大,优化目标会自适应地做出调整,增大优化目标中罚函数的权重,使得系统层与子问题层趋于统一。
3 火星探测器协同优化建模
火星探测器环绕火星的轨道为由捕获轨道调整而来的大椭圆轨道,有效载荷为中分辨率相机并采用三轴稳定模式,在近火弧段对火定向,载荷开展工作;远火弧段对日定向充电,太阳翼跟踪太阳方向。
3.1 系统级优化模型
3.1.1 系统优化目标
本文考虑的火星探测器以对火遥感任务为主,其有效载荷主要为中分辨率相机,在近火弧段(轨道高度低于800 km)对火星表面进行拍照,获得火星表面的科学数据。因此工程目标确定为对火遥感性能最佳,并使得整星重量尽可能低。综合考虑,采用加权法确定火星探测器的优化目标函数如下

其中:GSD为火表像元分辨率;φm为最大纬度覆盖范围,两者共同表征了遥感性能;为整星总重;分别为纬度覆盖、分辨率和总重的的归一化参数;为加权系数。

3.1.1 约束条件
为实现探测器对火遥感的科学任务要求,探测器的分辨率GSD和幅宽l应满足一定的要求;轨道太阳高度角以及光照角应满足光学载荷成像要求;整个电源系统满足能源平衡条件,蓄电池放电深度不宜过大;推进剂质量与探测器的整星质量满足相应的运载约束。因此总体设计需考虑的约束条件如表 1所示。
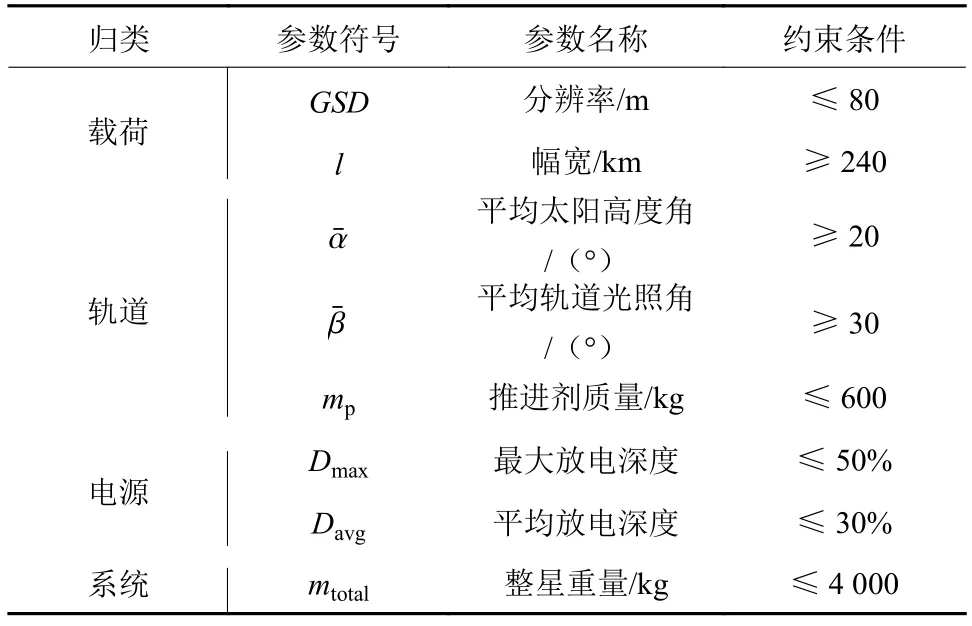
表1 探测器总体约束条件Table 1 The constraint of Mars probe
3.1.2 优化模型
综上所述,并采用动态罚函数将一致性约束加权到优化目标中,得到火星探测器的协同优化系统级优化模型为

其中:上标s表示该参数属于系统级参数;系统级变量包括与轨道学科相耦合的近火点高度远火点高度和轨道倾角;与载荷学科相耦合的相机焦距像元尺寸大小以及相机视场角与电源学科相耦合的太阳帆板面积;蓄电池容量和蓄电池个数一致性约束可表示为

3.2 学科模型
系统级模型建立后,就可以建立协同优化的学科优化模型,下面建立探测器的轨道、载荷和电源等学科的优化模型,对于各学科参数关于与设计变量的关系可参考各学科的专业书籍和文献,本文不作详细分析。
3.2.1 轨道学科分析
对于火星遥感探测器来说,轨道条件对任务功能的实现起至关重要的作用。探测器环绕火星的轨道由捕获轨道调整(包括调整近火点、远火点以及轨道倾角)而来,因此轨道学科可独立的设计变量为近火点高度hp,远火点高度ha以及轨道倾角i。探测器轨道的设计要满足一定的光照条件,即轨道太阳角β不能太小;同时为保证中分辨率相机在近火弧段能够正常拍照,在近火点处太阳高度角α需满足一定的条件;探测器每轨可成像时间决定了轨道的载荷有效工作时间。结合表 1,轨道学科的优化模型如下

3.2.2 载荷学科分析
载荷学科中,有效载荷为中分辨率CCD相机,以相机信噪比SNR、调制传递函数MTF、载荷数据率为约束条件,以相机的焦距f、像元尺寸大小d以及相机视场半张角η为载荷分系统设计变量。则有效载荷分系统的优化模型如下

3.3.3 电源学科分析
电源分系统负责为环绕器提供电能,其分系统设计分为太阳电池阵和蓄电池两部分。轨道参数是电源分系统设计的重要依据之一,轨道条件所决定的火影时间是电源系统设计时极为重要的输入条件。
电源分系统优化以太阳帆板面积Asa、蓄电池容量Cbat和个数选择为电源分系统设计变量,局部设计变量满足上下限约束的同时,也需满足蓄电池最大放电深度和平均放电深度等约束条件。因此得到电源学科的优化模型为

4 优化结果与分析
以2019年2月10日20时为到达窗口为例,捕获轨道参数为近火点高度600 km、远火点高度8万 km、捕获倾角30°。系统收敛条件为一致性约束J1≤ 10-4且J2≤10-4且J3≤ 10-4。系统级和学科级分别采用遗传算法(GA)和序列二次规划(SQP)优化算法对优化问题求解,其中GA算法在求解不可微、多峰值等优化问题上具有良好的全局求解能力;SQP算法则作为梯度优化算法,在求解非线性约束问题上具有很好的超线性收敛能力[11]。优化目标的迭代过程如图 2~5所示,设计变量的优化结果如表 2所示。
从图 2~5可以看出,一致性约束满足的终止条件是,迭代过程停止,各学科收敛达到协同一致,设计变量达到综合最优,系统优化目标满足最小化。要注意的是,虽然在第3次迭代时优化目标达到最小,但此时一致性约束条件并不满足终止条件,即各学科耦合变量并没有达到协同一致。当最后一致性约束Ji≤ 10-4时,此时优化目标才是综合最优,同时各学科约束条件满足要求,如表 3所示。

图2 一致性约束J1迭代过程图Fig.2 The iteration curve of consistency constraintJ1

图3 一致性约束J2迭代过程Fig.3 The iteration curve of consistency constraintJ2
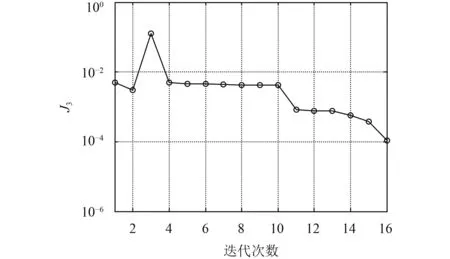
图4 一致性约束J2迭代过程Fig.4 The iteration curve of consistency constraintJ3

图5 优化目标F(X)迭代过程Fig.5 The iteration curve of optimization objective

表2 设计变量优化结果Table 2 the optimization results of design variable

表3 约束条件的优化结果Table 3 The optimization results of constraint
5 结 论
本文基于协同优化方法对火星探测器进行多学科协同优化建模,采用动态罚函数对系统一致性约束进行处理,以加快求解收敛速度。经过协同迭代,探测器的设计变量在使得优化目标最小且满足各个约束条件下达到整体最优,验证了协同优化方法应用于火星探测器总体参数优化的可行性和有效性。该方法可为火星探测器的总体设计提供一定的理论依据和技术参考。
[1]Wu B,Huang H,Wu W.A non-nested collaborative optimization method for multidisciplinary design problems[C]// 16th International Conference on Computer Supported Cooperative Work in Design(CSCWD).Wuhan:IEEE,2012.
[2]赵凡宇,徐瑞,崔平远.资源约束突破的航天器观测快速重调度优化算法[J].深空探测学报,2015,2(3):262-266.Zhao F Y,Xu R,Cui P Y.Measurement of fast recurrence of spacecraft observation based on resource constraint[J].Journal of Deep Space Exploration,2015,2(3):262-266.
[3]Braun R D.Collaborative optimization:an architecture for large-scale distributed design[D].California:Stanford University,1996.
[4]Zheng Y,Li G H,Fu J M.A distributed MDO architecture and its application on small satellite[C]//Proceedings of SPIE-The International Society for Optical Engineering.USA:[s.n],2009.
[5]Hwang J T,Lee D Y,Cutler J W.Large-scale MDO of a small satellite using a novel framework for the solution of coupled systems and derivatives[C]//Structural Dynamics and Materials Conference.Boston:AIAA,2013.
[6]San Scoucie M P,Hull P V,Tinker M L,et al.Lunar habitat optimization using genetic algorithms[R].USA:NASA,2007.
[7]裴晓强,黄海.协同优化在卫星多学科设计优化中的初步应用[J].宇航学报,2006,27(5):1054-1058.Pei X Q,Huang H.Application of collaborative optimization in multidisciplinary design optimization[J].Journal of Astronautics,2006,27(5):1054-1058.
[8]谭春林,庞宝君,张凌燕,等.对地观测卫星总体参数多学科优化[J].北京航空航天大学学报,2008,34(5):529-532.Tan C L,Pang B J,Zhang L Y,et al.Multidisciplinary optimization of the parameters of ground observation satellites[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(5):529-532.
[9]张凌燕.机动卫星总体多学科设计优化研究[D].北京:北京航空航天大学,2009.Zhang L Y.Study on the optimization of the overall multidisciplinary design of maneuvering satellites[D].Beijing:Beijing University of Aeronautics and Astronautics,2009.
[10]李海燕,井元伟,马明旭,等.基于动态罚函数法的协同优化算法[J].控制与决策,2009,24(6):911-915,920-921.Li H Y,Jing Y W,Ma M X,et al.Cooperation optimization algorithm based on dynamic penalty function method[J].Control and Decision,2009,24(6):911-915,920-921.
[11]李海燕,马明旭,黄章俊,等.自适应罚函数协同优化算法[J].系统仿真学报,2009,21(19):6178-6182.Li H Y,Ma M X,Huang Z J,et al.Adaptive penalty function cooptimization algorithm[J].Journal of System Simulation,2009,21(19):6178-6182.
[12]赖宇阳.Isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.Lai Y Y.Isight parameter optimization theory and examples[M].Beijing:Beihang University Press,2012.
Multidisciplinary Collaborative Optimization of Mars Probe Based on Dynamic Penalty Function
LIU Mingxing1,2,ZHANG Wei1,2,ZHANG Heng1,2,LIU Huaqing1
(1.Shanghai Institute of Satellite Engineering,Shanghai 201109,China;2.Shanghai Key Laboratory of Deep Space Exploration Technology,Shanghai 201109,China)
Focusing on the system design problem of Mars probe which is far away from the Earth and has the complex flight environment,the optimization function with comprehensive objective combined by coverage rate and ground sample distance was set up.Considering the orbit discipline,the payload discipline and the power discipline,the system-level and discipline-level optimization model of the Mars probe were established based on the cooperative optimization method,thus decomposing the complicated optimization problem into parallel cooperative optimization problems with multiple sub-disciplines.The adaptive dynamic penalty function is used to accelerate the convergence.The numeric results indicate that the collaborative optimization can be successfully applied in the system optimal design of Mars probe.
Mars probe;system optimal design;modeling;collaborative optimization;penalty function
V423.4
A
2095-7777(2017)03-0276-05
[责任编辑:宋宏,英文审校:任树芳]
10.15982/j.issn.2095-7777.2017.03.012
柳明星,张伟,张恒,等.基于动态罚函数的火星探测器多学科协同优化[J].深空探测学报,2017,4(3):276-280,292.
Reference format:Liu M X,Zhang W,Zhang H,et al.Multi-disciplinary collaborative optimization of Mars probe based on dynamic penalty function[J].Journal of Deep Space Exploration,2017,4(3):276-280,292.
2017-03-30
2017-05-06
柳明星(1990- ),男,助理工程师,主要研究方向:航天器多学科优化设计。
通信地址:上海市闵行区元江路3666号上海卫星工程研究所(201109)
电话:(021)24230432
E-mail:liumingxing_1990@163.com
