致密油藏复杂交叉Y型裂缝网络水平井产能及压力分析

杨立敏，田树宝，白兴，田冷，汪洋

（1.中国石油大学（北京）理学院，北京 102249；2.中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

致密油藏复杂交叉Y型裂缝网络水平井产能及压力分析

杨立敏1，田树宝2，白兴1，田冷2，汪洋1

（1.中国石油大学（北京）理学院，北京 102249；2.中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

针对水平井体积压裂产生的复杂交叉Y型裂缝网络，考虑裂缝交会处流量的重新分配，研究了致密油藏复杂交叉Y型裂缝网络压裂水平井的压力响应及产能变化规律，分析了裂缝形态（平行和交叉）、裂缝间距、裂缝闭合失效和井筒储集系数等因素的影响。结果表明：压开的裂缝网络越复杂，裂缝间距越小，无量纲井筒储集系数越小，则裂缝线性流出现得越晚，双线性流越明显且持续时间越长；压后闭合失效的裂缝位置和数量对水平井的动态产量和压力也有影响。通过比较、分析压后水平井的动态产量及压力响应曲线，对压后裂缝的有效性作出评价，为后期的压裂设计和施工提供指导。

致密油藏；复杂裂缝网络；水平井；多段压裂；星-三角变换法；产能分析；有效裂缝

水平井多段体积压裂是开发致密油藏的主体技术，与常规压裂的流动模式不同，在多段体积压裂后形成的裂缝网络的裂缝交会处存在流向的重新定向和流量的重新分配，这会显著影响水平井的生产动态。以往对多段压裂水平井产能及压力分析的研究大致可分为解析法［1-7］、半解析法［8-18］、数值法［19-23］。但是目前尚未有学者深入研究压裂形成的Y型交叉复杂裂缝网络中流体的渗流规律。本文考虑了致密油藏水平井多段体积压裂形成的复杂交叉Y型裂缝网络，建立了不稳定流动模型，研究了复杂交叉Y型裂缝网络中流体的流动分配规律，考察了复杂裂缝交叉、裂缝间距、井筒储集系数以及压后部分裂缝失效对水平井产能和压力响应的影响。

1 建立复杂交叉Y型裂缝网络模型

1.1 物理背景下的数学模型假设

在上下封闭的均质致密油藏中，经过体积压裂形成了复杂交叉Y型裂缝网络。假设地层、裂缝和流体微可压缩，压缩系数为常数，水平井只在与裂缝交叉处射孔，其他段封闭，裂缝纵向上贯穿储层。假设地层流体为单相黑油，地层和裂缝中的流体服从不稳定达西渗流。将裂缝网络离散成N个裂缝微元，在裂缝交叉处考虑流量的重新分配。

开采油藏时，流体从油藏流向裂缝，再流向水平井筒。将流体流动分为油藏流动和裂缝内部流动，假设井筒无限导流，分别为2种流动建模，再耦合压力和流量，建立压裂裂缝网络不稳态流动半解析模型。

1.2 油藏流动模型

1991年，Ozkan［24］提出了拉普拉斯空间中在不同边界条件下的点源函数。油藏流体流向裂缝时，等效于N个裂缝微元同时生产。应用势叠加原理，线源函数的叠加可模拟多个裂缝微元同时生产产生的干扰。第i个裂缝微元的压力卷积公式为

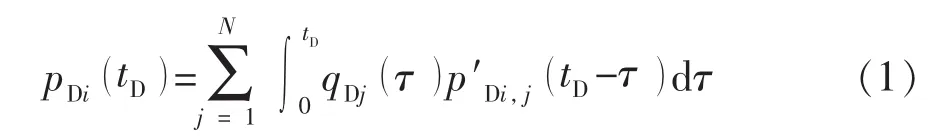
对式（1）进行拉普拉斯变换，并应用到所有裂缝微元，得到由N个等式构成的矩阵方程：

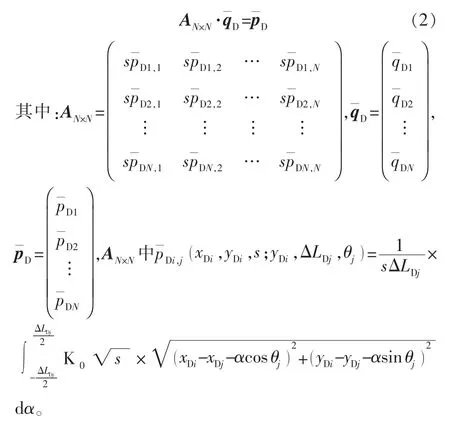
1.3 裂缝内部流动模型

假设裂缝中的流体呈一维流动，先给出裂缝中流体的流动方程。而对于复杂交叉裂缝网络，在裂缝相交处，又存在交汇流动，可将星-三角变换法应用于交会处的裂缝微元，进而得到修正后的更为真实的拟缝网流动方程。实空间下裂缝中不稳态流动方程的无量纲形式为

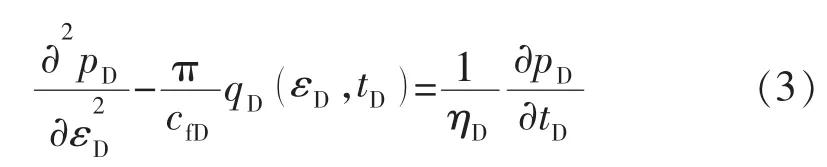
假设初始时刻下，油藏压力均匀分布，裂缝端部封闭，水平井定产量生产，则初始条件、内外边界条件分别为

tip指裂缝的顶端，wellbore指与井筒相接的裂缝微元。对式（3）和式（4）分别进行拉普拉斯变换，得：

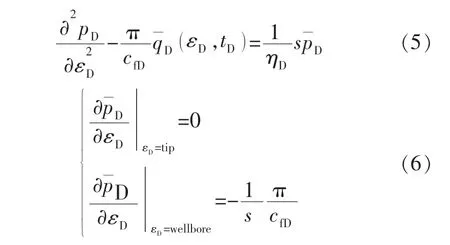
在裂缝微元上对式（5）离散化，得到有限差分方程：

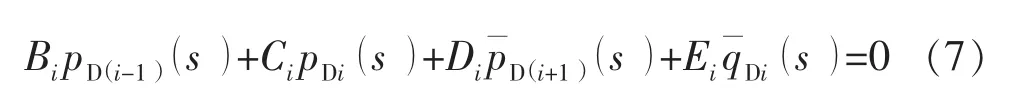
离散形式的关于式（6）的定产边界条件为

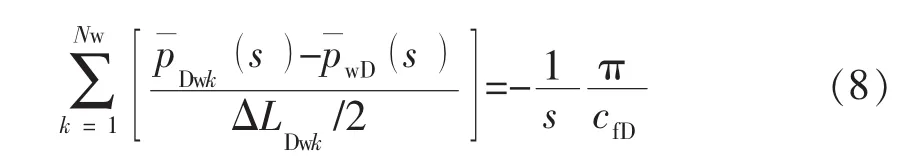
对于支裂缝交会处和主裂缝与支裂缝交会处的裂缝微元，采用星-三角变换法进行处理。参考Karimi［25］的交叉裂缝处理方法，定义了相邻裂缝之间的传导率，其中这样，2个裂缝微元之间的流量就可以用含有传导率的式子来表达，即Q12=对于交叉点处的裂缝微元，如图1中的裂缝微元1，在其上建立的有限差分方程与其左侧的裂缝微元和裂缝微元0有关；而对于裂缝微元0，并没有相应的有限差分方程，同时裂缝微元0与裂缝微元2和3的有限差分方程有关。通过如图2所示的变换，消去交会处的裂缝微元0，使裂缝微元1，2，3直接相邻，则流体在裂缝交会处的流向和流量由交会点处的裂缝微元的压力和传导率自动决定，变换后相邻裂缝微元间的传导率计算公式为这样即可将裂缝交叉处的裂缝微元对缝网的影响分摊到与其相邻的其他裂缝微元中。

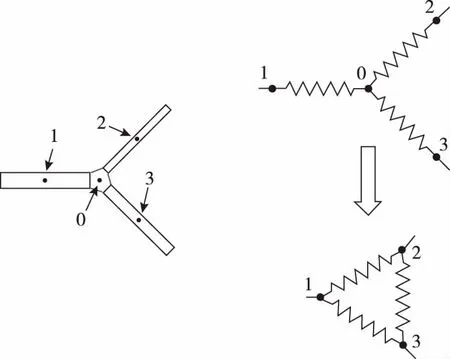
图1 交叉处裂缝微元的处理方法示意

1.4 求解不稳态流动模型

将油藏流动方程、裂缝流动方程和边界条件耦合，即将式（2）、式（7）和式（8）耦合得矩阵方程：

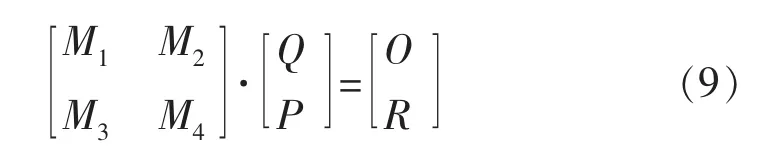
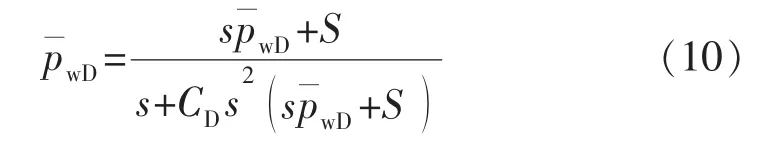
这是一个包含井筒存储效应和表皮系数对压力的影响的结果。其中

水平井定产量生产时的井底流压p¯wD和水平井定井底流压生产时的产量之间关系式为

用数值代数方法求解矩阵方程（9），用 Stehfest于1970年提出的方法反演式（10）和式（11），由此可得实空间下的压力和动态产量。

2 水平井压力响应及产能影响因素

2.1 裂缝网络形态

图2为在定产条件下2条直线型平行裂缝和2条复杂交叉裂缝的压力动态双对数曲线。横坐标无量纲时间tD值10-6，10-5，10-4，10-3，10-2，10-1，100，分别对应的油井生产时间为3.36min，33.60min，5.6 h，56.0 h，23.3 d，233.0 d，2333.0 d。从图3可以看出，裂缝网络越复杂（Y型交叉裂缝），井筒储集流持续时间越长，则裂缝线性流出现越晚，双线性流越明显且持续时间越长。

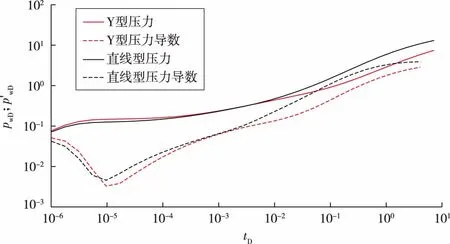
图2 2条直线型平行裂缝和2条复杂交叉裂缝压力动态对比

图3为在定压条件下2条直线型平行裂缝和2条复杂交叉裂缝的动态产量双对数曲线。从图中可以看出，在水平井投产早期（tD＜10-3，生产时间少于56.0 h），直线型平行裂缝井的产量高于复杂交叉裂缝井的产量，但持续时间很短（2 d左右），随着生产时间的延长，复杂交叉裂缝井的产量高于直线型平行裂缝井的产量。说明对于致密油藏水力压裂，人工压开的主裂缝贯穿沟通的天然裂缝越多，提高产量的效果越好。

图3 2条直线型平行裂缝和2条复杂交叉裂缝动态产量对比

2.2 裂缝间距

为了比较不同裂缝间距对曲线形态的影响，使井筒长度保持一致，Y型裂缝数目从5条增加到9条。如图4所示，在水平井投产初期（tD＜10-4，生产时间少于5.6 h），不同裂缝间距井的产量差别不大，但该趋势持续时间很短（5.0 h左右）。随着生产时间的延长，压开的裂缝越多，水平井产量越高。但裂缝数目越多的水平井，后期产量递减越快，因为在水平井总长度不变的条件下，裂缝间距减小，裂缝区渗流相互干扰更加明显。存在一个最优的裂缝条数（本算例为8条裂缝最优（蓝色线）），使水平井产量达到最优。

图4 不同裂缝区间下水平井生产时的动态产量双对数曲线

2.3 裂缝闭合失效

在实际致密油藏水平井多段压裂施工中，由于地层因素的影响、施工工艺等原因导致有的压开裂缝可能在停泵后闭合失效。本文考虑了水平井压裂完成后其中某几条裂缝闭合失效对渗流规律的影响。

2.3.1 对压力响应的影响

图5显示了5条裂缝中3条裂缝闭合失效的情况下（图中虚化的Y型裂缝为闭合失效的裂缝）。3条失效裂缝处于不同位置时，井底动态压力与压力导数的双对数曲线。当3条裂缝失效，只有2条裂缝生产时的压力曲线与5条裂缝全部生产时的曲线在生产中期存在较明显的差别，后者双线性流更明显且持续时间更长。生产初期，失效裂缝的位置变化对水平井压力响应曲线影响不明显，但在生产中后期，影响显著。

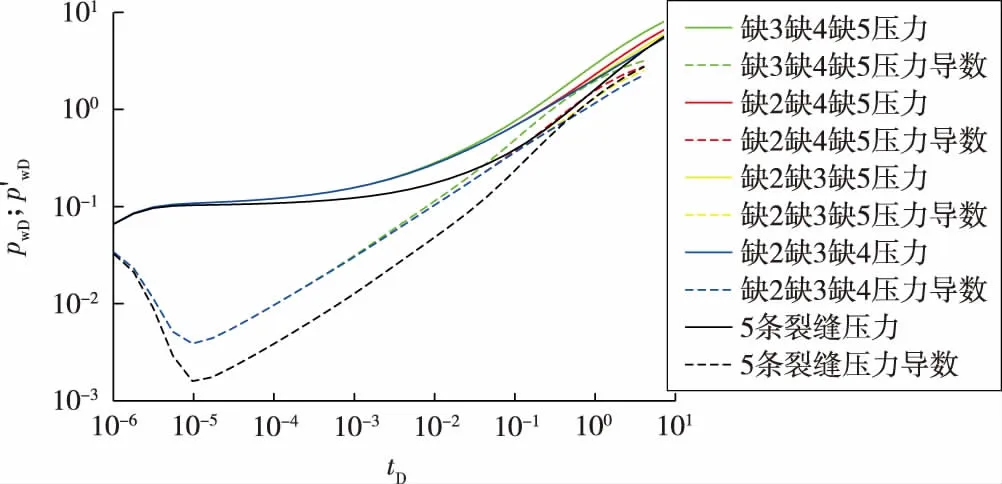
图5 5条裂缝中3条失效的水平井动态压力双对数曲线

2.3.2 对产能的影响

图6显示了在5条裂缝中3条裂缝闭合失效的情况下，这3条失效裂缝处于不同位置时，水平井的动态产量双对数曲线（图中虚化的Y型半支裂缝为闭合失效的裂缝）。当3条裂缝失效，只有2条裂缝生产时的产量曲线与5条裂缝全部生产时的曲线（黑色线）明显不同。生产初期和中期，后者的产量明显高于前者，但在生产后期递减较快；生产后期，中间3条缝失效的水平井产量（蓝色线）较高，因为此时生产的2条裂缝相距最远，相互之间的干扰最小。

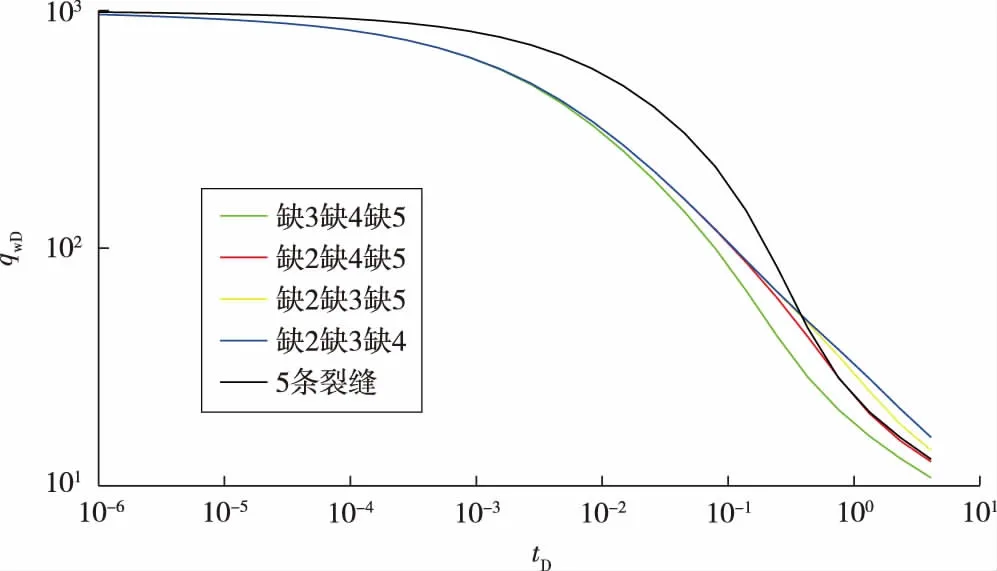
图6 5条裂缝中3条失效的水平井动态产量双对数曲线

2.4 井筒储集系数

图7显示了不同井筒储集系数下，压开5条裂缝水平井的动态压力与压力导数双对数曲线。从图中可以看出，井筒储集效应在水平井投产初期（tD＜10-4）影响明显。无量纲井筒储集系数越小，则双线性流出现得越早且持续的时间越长。

图7 5条裂缝水平井生产时的动态压力双对数曲线

3 结论

1）水平井压开裂缝网络越复杂，裂缝间距越小，无量纲井筒储集系数越小，则裂缝线性流出现得越晚，双线性流越明显且持续的时间越长。

2）针对压裂形成的复杂裂缝网络，存在一个最优的裂缝网络配置，可使水平井产量达到最优。

3）分析了压后闭合失效的Y型裂缝所处位置对水平井产量及压力变化的影响，以及水平井产量和压力受闭合失效的裂缝位置和数量的影响。通过比较、分析压后水平井的动态产量及压力响应曲线，可以评价压后裂缝的有效性，有利于后期压裂设计和施工。

4 符号注释

K为油藏渗透率，m2；φ为油藏孔隙度；h为油藏厚度，m；pe为原始地层压力，MPa；μ为地层流体黏度，mPa·s；B为地层流体体积系数；ct为综合压缩系数，MPa-1；qw为井产量，m3/d；t为时间，h；pi为裂缝微元 i的压力，MPa；qi为油藏流向裂缝微元i的流量，m3/d；)为裂缝微元i的几何中心坐标；△Li为裂缝微元i的长度，m；φi为裂缝微元i的孔隙度；cti为裂缝微元的压缩系数；ε为裂缝方向；h1为参考长度，m；s为拉普拉斯变量；θ为裂缝微元与x轴的夹角，（°）；K0为0阶第2类修正贝塞尔函数；Bi，Ci，Di和Ei为系数；Nw为与井筒相连的裂缝微元个数；为与井筒相连的无因次裂缝微元压力；△LwD为与井筒相连的无因次裂缝微元长度；Ai为2个控制体交界面区域；Di为交界面与CVi的几何中心之间的距离；ni为交界面处指向控制体的单位法线；fi为从交界面的中心指向控制体中心的单位向量；S为表皮系数；CD为无因次井筒存储系数。下标w，D分别表示生产井、无因次。

［1］BROWN M，OZKAN E，RAGHAVAN R，et al.Practical solutions for pressure transientresponses offractured horizontalwells in unconventional shale reservoirs［J］.SPE Reservoir Evaluation& Engineering，2011，14（6）：663-664.

［2］EZULIKE D O，HAWKES R V，DEHGHANPOUR H.Understanding flowback as a transient 2-phase displacement process：an extension of the linear dual-porosity model［R］.SPE 167164，2013.

［3］OZKAN E，BROWN M.Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs［R］.SPE 121290，2009.

［4］SOLIMAN M Y，HUNT J L，EL-RABAA A M.Fracturing aspects of Horizontal Wells［J］.Journal of Petroleum Technology，1990，42（8）：966-973.

［5］STALGOROVA E，MATTAR L.Practical analytical model to simulate production of horizontal wells with branch fractures［R］.SPE 162515，2012.

［6］XU B，LI X，HAGHIGHI M，et al.Development of new type curves for production analysis in naturally fractured shale gas/tight gas reservoirs［C］.Beijing：InternationalPetroleumTechnologyConference，2013.

［7］ZHAO Y，ZHANG L，LUO J，et al.Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir［J］.Journal of Hydrology，2014，512（10）：447-456.

［8］CHEN C，RAGHAVAN R.A multiply-fractured horizontal well in a rectangular drainage region［J］.SPE Journal，1997，2（4）：455-465.

［9］CROSBY D G，RAHMAN M M，RAHMAN M K，et al.Single and multiple transverse fracture initiation from horizontal wells［J］. Petroleum Science and Engineering，2002，35（3/4）：191-204.

［10］GUO G，EVANS R D.Pressure-transient behavior and inflow performance of horizontal wells intersecting discrete fractures［R］.SPE 26446，1993.

［11］HORNE R N，TEMENG K O.Relative productivities and pressure transient modeling of horizontal wells with multiple fractures［R］.SPE 29891，1995.

［12］LARSEN L，HEGRE T M.Pressure-transient behavior of horizontal wells with finite-conductivity vertical fractures［R］.SPE 22076，1991.

［13］LUO W，TANG C，WANG X.Pressure transient analysis of a horizontal well intercepted by multiple non-planar vertical fractures［J］.Journal of Petroleum Science and Engineering，2014，124：232-242.

［14］MEDEIROS F，OZKAN E，KAZEMI H.Productivity and drainage area of fractured horizontal wells in tight gas reservoirs［R］.SPE 108110，2007.

［15］WAN J，AZIZ K.Semi-analytical well model of horizontal wells with multiple hydraulic fractures［J］.SPE Journal，2002，7（4）：437-445.

［16］ZERAR A，TIAB D，BETTAM Y.Interpretation ofmultiple hydraulically fractured horizontal wells［R］.SPE 88707，2004.

［17］ZHOU W，BANERJEE R，POE B D.Semi-analytical production simulation of complex hydraulic fracture networks［R］．SPE 157367，2012．

［18］JIA P，CHENG L，HUANG S，et al.A semi-analytical model for transient flow behavior of hydraulic fracture networks［J］.Journal of China University of Petroleum，2015，39（5）：107-116.

［19］AL-KOBAISI M，OZKAN E，KAZEMI H.A hybrid numerical analytical model of finite conductivity vertical fractures intercepted by a horizontal well［R］.SPE 92040，2004.

［20］FREEMAN C.A numerical study of microscale flow behavior in tight gas and shale gas［R］.SPE 14125，2010.

［21］KARCHER B J，GIGER F M，COMBE J.Some practical formulas to predict horizontal well behavior［R］.SPE 15430，1986.

［22］OLORODE O M，FREEMAN C M，MORIDIS G J，et al.Highresolution numerical modeling of complex and irregular fracture patterns in shale gas and tight gas reservoirs［R］.SPE 152482，2012.

［23］VALKO P P，AMINI S.The method of distributed volumetric sources for calculating the transient and pseudo-steady state productivity of complex well-fracture configurations［R］.SPE 106279，2007.

［24］OZKAN E，RAGHAVAN R.New solutions for well-test-analysis problems：computational considerations and applications［J］．SPE Formation Evaluation，1991，6（3）：369-378.

［25］KARIMI-FARD M，DURLOFSKY L J，AZIZ K．An efficient discretefracture model applicable for general-purpose reservoir simulators［J］. SPE Journal，2004，9（2）：227-236．

（编辑 孙薇）

Productivity and pressure response of complex Y-shape hydraulic fracture networks in tight oil reservoirs

YANG Limin1,TIAN Shubao2,BAI Xing1,TIAN Leng2,WANG Yang1
(1.College of Science,China University of Petroleum,Beijing 102249,China;2.MOE Key Laboratory of Petroleum Engineering, China University of Petroleum,Beijing 102249,China)

Considering the redistribution of oil flow in the intersection of fracture in the complex fracture network,the productivity and pressure response of hydraulic fracturing horizontal well with complex Y-shape hydraulic fracture networks was studied.The effects of factors such as fracture shape(parallel and cross),fracture interval,ineffective fracture and wellbore storage coefficient were analyzed.The results show that the more complex the fracture networks,the less the fracture interval,the smaller the wellbore storage coefficient result in the later the fracture liner flow,the more obvious the bilinear flow and the longer the bilinear flow.The location and amount of the ineffective fractures also have influences on the productivity and pressure of the horizontal well.By the observation,comparison and analysis of the productivity and pressure response curves of the horizontal well,the effectiveness of the constructed fractures can be evaluated,which can help to design and construct hydraulic fracturing in tight oil reservoirs.

tight oil reservoir;complex fracture network;horizontal well;multi-fracturing;star-delta transformation;analysis of productivity;effective fracture

TE33+1

A

国家自然科学基金项目“基于声震效应的页岩储层多组分流体多场耦合流动机理”（U1562102）

10.6056/dkyqt201705019

2017-02-20；改回日期：2017-06-26。

杨立敏，女，1970年生，副教授，1995年毕业于四川大学数学专业，现从事算子理论和油气田开发研究。E-mail：ylm@cup.edu.cn。

杨立敏，田树宝，白兴，等.致密油藏复杂交叉Y型裂缝网络水平井产能及压力分析［J］.断块油气田，2017，24（5）：682-686.

YANG Limin，TIAN Shubao，BAI Xing，et al.Productivity and pressure response of complex Y-shape hydraulic fracture networks in tight oil reservoirs［J］.Fault-Block Oil&Gas Field，2017，24（5）：682-686.