一种基于接触性理论的储层裂缝闭合新模型

王一帆，丁高翔，曹嘉斌，曹猛，尤雪尘，黄东安

（1.中国石油大学（北京）石油工程教育部重点实验室，北京 102249；2.中国石油长庆油田分公司第十一采油厂，甘肃 庆阳 745000）

一种基于接触性理论的储层裂缝闭合新模型

王一帆1，丁高翔2，曹嘉斌2，曹猛1，尤雪尘1，黄东安2

（1.中国石油大学（北京）石油工程教育部重点实验室，北京 102249；2.中国石油长庆油田分公司第十一采油厂，甘肃 庆阳 745000）

运用弹塑性理论，提出了一种更加合理的基于微观结构的新型裂缝闭合模型。在新模型中，首先，运用经典的接触力学理论，将裂缝表面微凸体受挤压状态分为完全弹性变形、弹塑性变形和完全塑性变形3个阶段，并且假设弹塑性变形阶段光滑且连续地衔接其他2种变形。为了更好地描述衔接过程，采用了样板函数，连接完全弹性变形和完全塑性变形状态方程，进而得出微凸体受挤压而压缩整个过程的数学模型。随后，引入当前关于概率分布的理论，合理优化出因为表面的微凸体受压缩而导致裂缝闭合的状态模型。最后，使用新模型模拟出裂缝闭合量随各项参数的变化，并与已有的完全弹性模型、完全塑性模型进行对比。结果表明，新模型中裂缝闭合量随各参数的变化介于完全弹性模型和完全塑性模型之间，裂缝受到有效应力而闭合的状态也更加符合预期，可以合理地体现裂缝逐渐闭合的状态。

天然裂缝；裂缝闭合模型；微凸体；弹塑性理论

0 引言

目前针对储层中天然裂缝闭合问题的研究主要包括以室内实验为主的宏观研究和以裂缝微观结构为基础的微观研究。虽然以实验为基础的研究能够揭示应力作用情况下裂缝闭合的普遍规律，但由于储层裂缝发育的情况复杂多变，实验得出的结果并不能很好地应用于评价各类油藏储层的应力敏感性［1］。微观研究充分考虑了裂缝及岩石本身的各项性质，能较好地说明各类参数对于岩石裂缝闭合的影响，因此针对裂缝闭合特征的微观研究成为当前和以后的发展趋势［2］。

Greenwood等［3］采用Hertz所提出的弹性接触理论对粗糙平面与光滑平面接触挤压的问题进行研究，并形成了被广泛接受的G&W模型；Yamada等［4］则根据粗糙表面的随机性建立了微观条件下裂缝弹性接触模型；Walsh等［5］随后基于G&W模型对裂缝受挤压过程中的变形问题做了研究，并揭示出了裂缝闭合量与裂缝表面微凸体高度分布标准差存在的关系；Brown和Scholz［6-7］针对裂缝闭合的相关问题做了大量工作，改进了G&W模型，并形成了B&S模型；张仕强［8］对砂岩岩心进行了相关的测量，并采用分形方法对裂缝表面特征进行了表述，也建立了相关模型；段玉廷［9］在前人的基础上对裂缝的弹性接触问题和塑性接触问题进行了研究；王一帆等［10］对微观条件下裂缝的闭合规律进行了研究。

本文在前人研究的基础之上，提出了一种基于接触性理论的储层裂缝闭合新模型，并进行了相关的分析和对比。

1 模型建立

1.1 单个微凸体挤压变形模型

由于将裂缝的闭合问题转化成了微凸体的变形问题，所以应首先针对单个微凸体的受力变形情况进行研究。如图1所示（其中R为微凸体半径），受有效应力ωε的作用，微凸体产生了形变量δ。

式中：z为相对于复合表面基准面的高度，μm；d为微凸体平均高度相对于基准面的距离，μm。

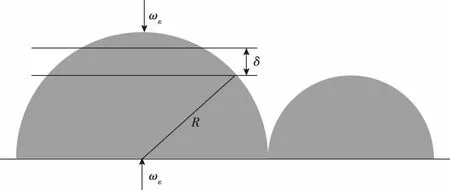
图1 单个微凸体受光滑平面挤压示意

1.1.1 弹性压缩阶段

当形变量较小时，微凸体产生弹性变形。微凸体和光滑平面之间的接触面积Ae为

依据Hertz弹性接触理论，微凸体所受光滑平面挤压的法向应力Ne为

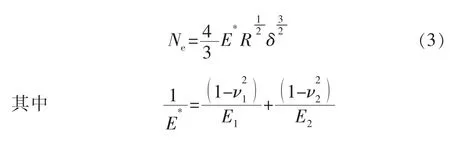
完全弹性变形时的平均接触压力pe为

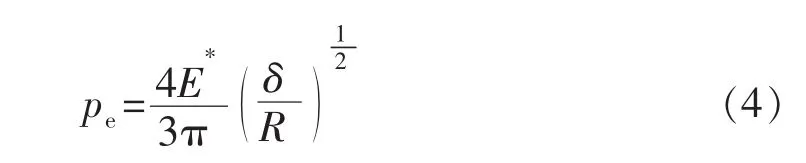
微凸体形变量增加到一定值时，微凸体发生初始屈服，并发生部分区域的塑性变形。发生初始屈服时微凸体的形变量δ1为

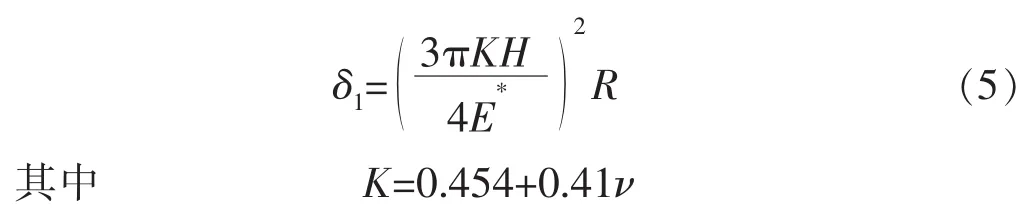
当微凸体的形变量比δ1小时，产生弹性压缩；当微凸体的形变量比δ1大时，则产生弹塑性压缩或者塑性压缩。其临界平均接触压力为

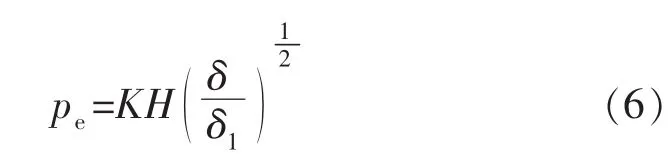
式中：E为弹性模量，MPa；E*为复合裂缝表面微凸体的等效弹性模量，MPa；E1，E2分别为复合前裂缝上、下表面的弹性模量，MPa；ν为泊松比；ν1，ν2分别为复合前裂缝上、下表面的泊松比；H为岩石的硬度，MPa；K为岩石的平均接触压力系数。

1.1.2 塑性压缩阶段

当微凸体的形变量增加到足够大时，将产生完全塑性压缩。产生完全塑性压缩的微凸体临界形变量δ2= 110δ1［9］。当微凸体的形变量δ≥δ2时，微凸体产生塑性压缩，根据Abbott等［10］的研究，其接触面积Ap=2πRδ。产生塑性变形时，微凸体和光滑平面接触面上的压力是均匀的，都等于裂缝岩石的硬度值［11］，即pp=H，那么在微凸体塑性压缩阶段的法向应力Np为

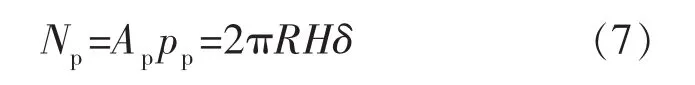
1.1.3 弹塑性压缩阶段

当δ1≤δ＜δ2时，为弹塑性压缩阶段。在这个阶段中，法向应力、形变量、接触面积三者的关系变得很复杂［12］。依据连续介质力学理论，由弹性压缩状态向弹塑性压缩状态过渡的过程为连续并且光滑的。在法向应力不断增大的过程中，塑性变形逐渐变成主要状态，弹性变形作用逐渐减小［13-15］，2个临界点处的平均接触压力、形变量、接触面积的关系为

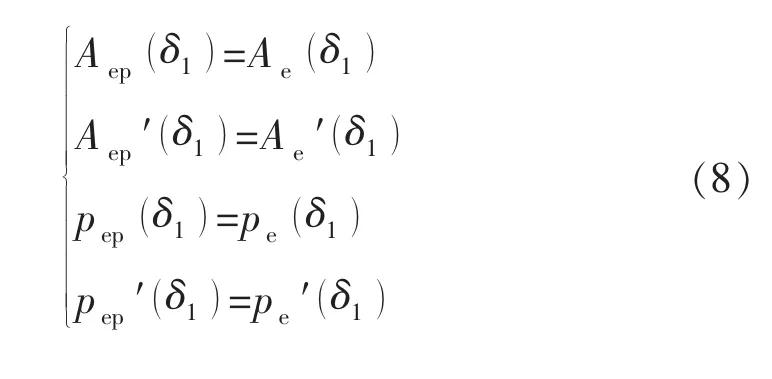
式中：Aep为微凸体弹塑性压缩时的接触面积，μm2；pep为微凸体弹塑性压缩时的平均接触压力，MPa；A′，p′分别为接触面积函数和接触压力函数的导数。

为光滑连续地连接3种变形状态，现构建1个样板函数，使其在［0，1］内单调增加：

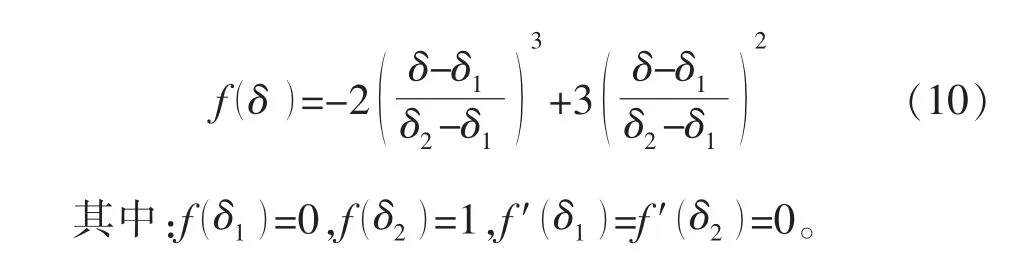
此外，再假设2个函数：images/P60_4774.jpgimages/P60_4775.jpg假如某函数在δ1和δ2处与这2个函数连续并且光滑地衔接，此时该函数也应该同时满足含有样板函数的关系：

Aep，pep都可以满足式（8），（9）光滑连续衔接的临界条件，且单调递增。

1.2 裂缝闭合模型

在法向应力逐渐增大的过程中，裂缝闭合量增加，受挤压变形的微凸体个数也增加。由上、下表面复合而成的表面上微凸体的高度函数与高斯分布相符合，即：

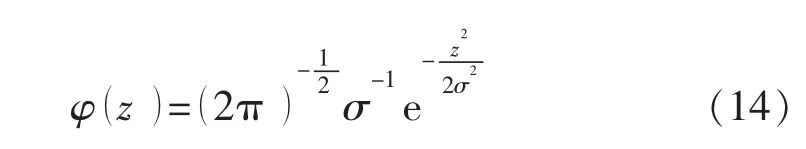
在复合而成的表面与光滑平面相互接触的过程，即复合而成的表面上微凸体与光滑平面相互接触的过程，分别就完全弹性压缩、弹塑性压缩和完全塑性压缩的各项数值积分求和，得出接触的状态，则有：

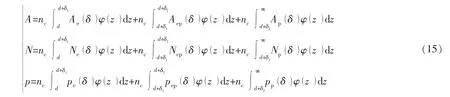
式中：A为两表面的接触面积，μm2；N为两表面总的法向应力，MPa；p为两表面的平均接触压力，MPa；nc为复合粗糙表面上微凸体与光滑平面接触的数量；η是微凸体的单位面积密度；An为名义接触面积，μm2。

由式（15）可得：

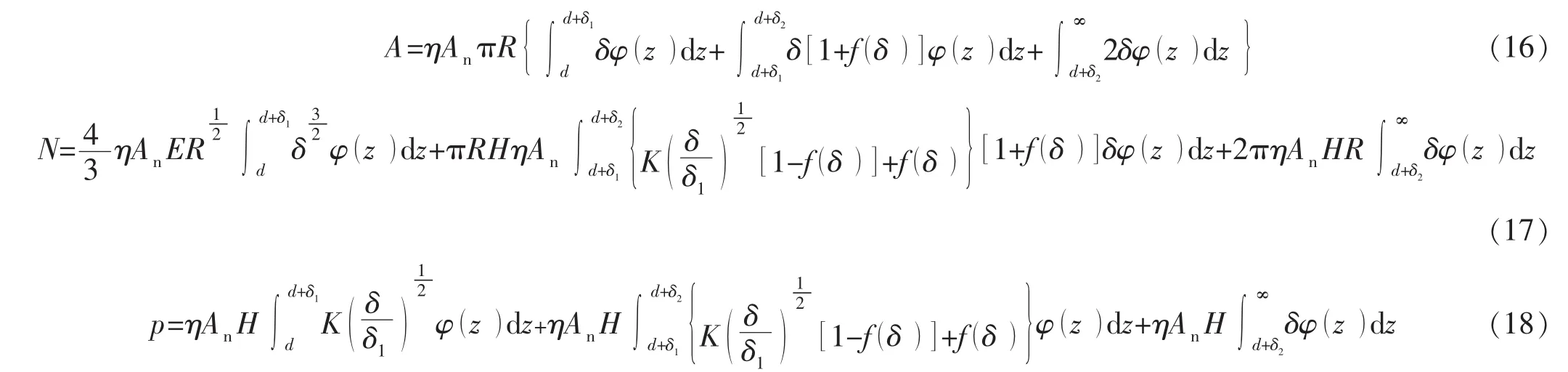
2 模型对比验证

对参数进行归一化处理。将本文所建模型的计算结果与完全弹性模型和完全塑性模型的计算结果进行对比，结果见图2—6。

如图2所示，受微凸体压缩状态的影响，同一闭合量下，不同压缩状态的接触面积不同，最终闭合时的接触面积也存在差异。当产生完全塑性变形的微凸体和光滑平面之间的接触面积到达最大值时，完全弹性变形情况下的微凸体和光滑平面之间的接触面积仅为前者的二分之一，且由于样板函数光滑、连续地衔接2种变形，并在［0，1］区间内变化，因此本文模型中的接触面积可达到完全塑性状态最终值。此外，在同一接触面积情况下，弹性变形时裂缝的闭合量最大，塑性变形时裂缝的闭合量最小，本文模型下裂缝的闭合量介于两者之间，符合客观规律和预期。

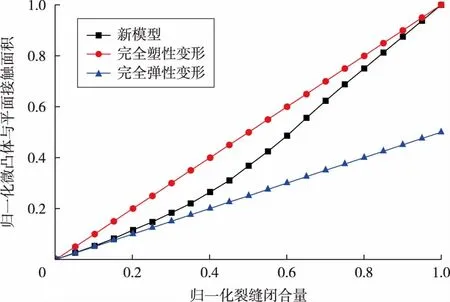
图2 单个微凸体接触面积与裂缝闭合量的关系

图3为模拟上表面和下表面接触面积随裂缝闭合量变化的曲线。在初始情况下，由于微凸体高度基准面、接触微凸体数量的影响，裂缝产生闭合时两表面的接触面积增加较快，但是在闭合量增加的过程中，裂缝闭合所受到的抵抗力增加，接触面积增加较慢。除此之外，接触面积相同时，完全弹性变形时裂缝的闭合量最大，完全塑性变形时最小，新建模型介于两者之间。

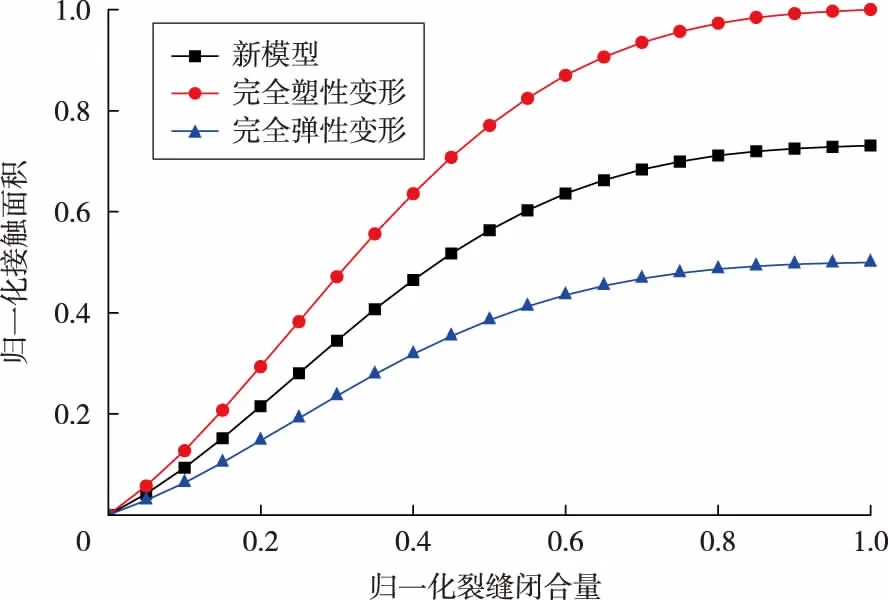
图3 上、下表面接触面积与裂缝闭合量的关系

由图4、图5可以看出：受样板函数对完全塑性变形和完全弹性变形衔接的影响，相同闭合量时，本文新模型所求得的接触压力介于完全塑性和完全弹性变形之间。此外，受到裂缝闭合的影响，新模型中接触压力的增加速率逐渐变缓，且单个微凸体接触压力最终达到和完全塑性变形时一样，这也进一步说明样板函数起到较好的作用，计算结果符合客观规律。在研究上表面和下表面之间的接触压力和闭合量之间的关系时可发现，由于裂缝的闭合量受到法向应力的影响，因此平均接触压力同时受到接触面积和法向应力的影响，在闭合初期，完全弹性变形时的接触压力比较小，但随着法向应力增加，闭合量变大，完全弹性变形的接触压力超过完全塑性变形的接触压力。

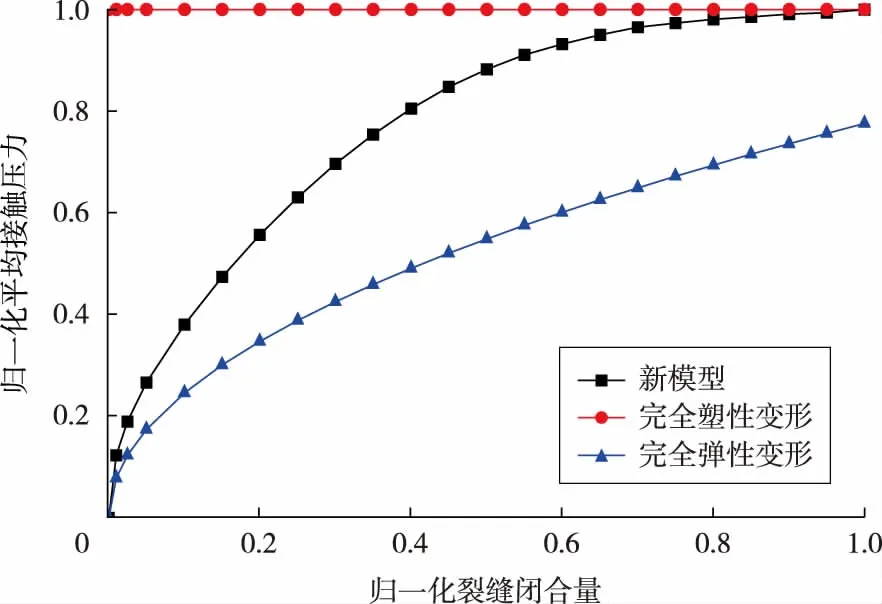
图4 单个微凸体平均接触压力与裂缝闭合量的关系

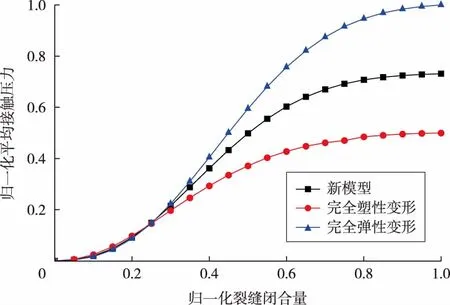
图5 上、下表面平均接触压力与裂缝闭合量的关系

图6为各个模型中闭合量随法向应力变化的对比曲线。

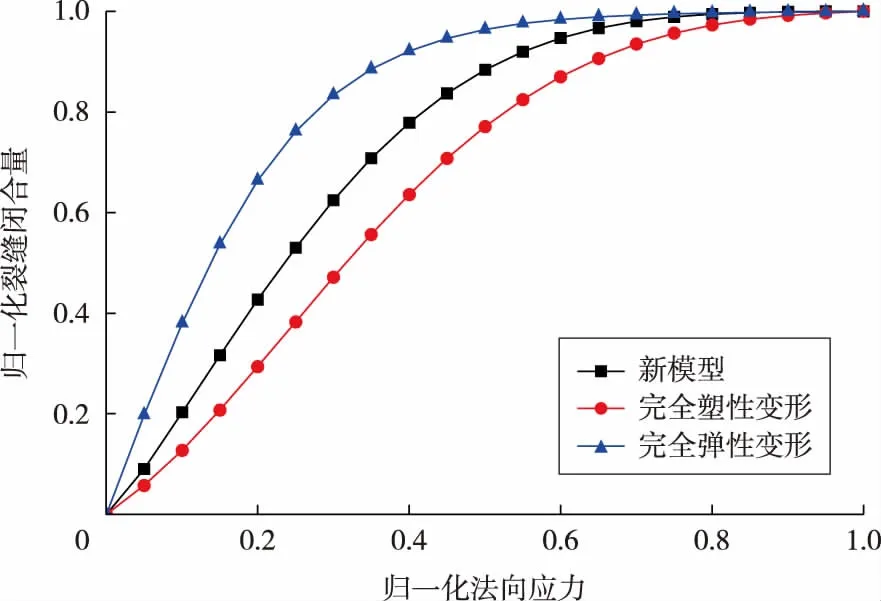
图6 裂缝闭合量随法向应力的变化

图6中，3种模型情况下，裂缝闭合量随法向应力变化的规律保持基本一致，即裂缝初始闭合时，裂缝闭合速率较大，由于受到法向应力的影响，裂缝闭合量逐渐增加，但裂缝的闭合速率在逐渐减小。出现这种现象是由于裂缝闭合量的不同，所受到的微凸体支撑力也不同，裂缝的闭合难度随着闭合量的增加而变大。此外，不同的接触状态也影响着裂缝闭合的难易程度，因此裂缝达到最大闭合量的先后顺序不同。由图可知，完全弹性变形情况下裂缝闭合量达到最大值最早，而完全塑性变形达到最大值最晚，新建模型情况下裂缝闭合次序介于两者之间。

3 结论

1）新模型能够较好地描述裂缝闭合时各项指标的变化规律，可以很好地模拟裂缝闭合的状态，在解决相关问题时具有合理性和实用性。

2）在闭合过程中，单个微凸体和光滑表面的接触面积、平均接触压力与裂缝的闭合量之间并非简单的线性关系，而是裂缝闭合量越大，接触面积的增长速率越大，平均接触压力增长速率越小。

3）在闭合过程中，裂缝上、下表面平均接触压力与裂缝闭合量之间呈“S”形曲线关系，随着裂缝闭合量的增加，上、下表面平均接触压力的增长速率经历了先逐渐增大后逐渐减小的过程。

［1］肖文联，李滔，李闽，等.致密储集层应力敏感性评价［J］.石油勘探与开发，2016，43（1）：107-114.

［2］刘向君，刘战君，李允，等.裂缝闭合规律研究及其对油气田开发的影响［J］.天然气工业，2004，24（7）：39-41.

［3］GREENWOOD J，WILLIAMSON J.Contact of nominally flat surfaces［J］.Proceedings ofthe RoyalSociety ofLondon：Series A Mathematical and Physical Sciences，1966，295（1442）：300-319.

［4］YAMADA K N，TAKEDRA J，KAGAMI T N.Mechanism of elastic contact and friction between rough surface［J］.Wear，1978，48（1）：15-34.

［5］WALSH J B，GROSENBAUGH M A.A new model for analyzing the effect of fractures on compressibility［J］.Journal of Geophysical Research Solid Earth，1979，84（B7）：3532-3536.

［6］BROWN S R，SCHOLZ C H.Closure of random elastic surfaces in contact［J］.Journal of Geophysical Research Atmospheres，1985，90（90）：5531-5545.

［7］BROWN S R，SCHOLZ C H.Closure of rock joints［J］.Journal of Geophysical Research，1986，91（B5）：4939-4948.

［8］张仕强.裂缝形态描述及其力学、流动特性分析［D］.南充：西南石油学院，1997.

［9］段玉廷.裂缝、裂缝-孔隙性复杂介质储层的损害机理研究［D］.南充：西南石油学院，1998.

［10］王一帆，辛一男，赵超，等.微观条件下储层天然裂缝闭合特征研究［J］.科学技术与工程，2016，16（17）：32-35.

［11］CHANG W R，ETSION I，BOGY D.Static friction coefficient model for metallic rough surfaces［J］.Journal of Tribology，1988，110（1）：57-63.

［12］WADWALKAR S S，JACKSON R L，KOGUT L.A study of the elasticplastic deformation of heavily deformed spherical contacts［J］. Proceedings of the Institution of Mechacnical Engineers，2010，1（1）：1-12.

［13］ABBOTT E J，FIRESTONE F A.Specify surface quality：a method based on accurate measurement and comparison［J］.Mechanical Engineers，1933，55：569-572.

［14］冯金德，程林松，李春兰，等.裂缝性低渗透油藏等效连续介质模型［J］.石油钻探技术，2007，35（5）：94-97.

［15］聂法健，田巍，国殿斌，等.深层高压低渗透储层应力敏感性研究［J］.断块油气田，2016，23（6）：788-792.

（编辑 史晓贞）

New model of natural fracture closure based on microstructure

WANG Yifan1,DING Gaoxiang2,CAO Jiabin2,CAO Meng1,YOU Xuechen1,HUANG Dong′an2
(1.MOE Key Laboratory of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.No.11 Oil Production Plant,Changqing Oilfield Company,PetroChina,Qingyang 745000,China)

Based on the elastic-plastic theory,a more reasonable fracture closure model is proposed.First,the classical theory of contact mechanics is applied,and the squeezed state of fracture surface asperities is classified into complete elastic deformation, elastic plastic deformation and full plastic deformation.In addition,it is assumed that the elastic-plastic deformation state is smooth and continuous with the other two kinds of deformation.In order to represent the joining process of complete elastic deformation and full plastic deformation properly,a template function is employed.Then the mathematical model of the whole process of the compression of the asperity is obtained.Subsequently,the theory of probability distribution is introduced to optimize the state model of fracture closure due to compression of the surface asperity.Finally,the new model is used to simulate the variation of fracture closure with various parameters,and compared with the results of existing complete elastic model and the fully plastic model.The results of the new model is in the mid of other two models,which is more in line with expectations and reasonably shows the state of the fracture closing process.

natural fracture;model of fracture closure;asperity;elastic-plastic theory

TE122

A

国家自然科学基金项目“硬脆/塑性泥页岩微裂缝产生的岩石物理学机制基础研究”（41572130）

10.6056/dkyqt201705012

2017-03-21；改回日期：2017-07-12。

王一帆，男，1992年生，在读硕士研究生，现从事非常规油气田开发相关方面的研究。E-mail：284068991@qq.com。

王一帆，丁高翔，曹嘉斌，等.一种基于接触性理论的储层裂缝闭合新模型［J］.断块油气田，2017，24（5）：652-656.

WANG Yifan，DING Gaoxiang，CAO Jiabin，et al.New model of natural fracture closure based on microstructure［J］.Fault-Block Oil&Gas Field，2017，24（5）：652-656.