基于高阶Cauchy-Born准则的平面应变梯度结构监测理论研究★

吕 娜 侯东昌 孙玉周

(中原工学院建筑工程学院，河南 郑州 450007)

基于高阶Cauchy-Born准则的平面应变梯度结构监测理论研究★

吕 娜 侯东昌 孙玉周

(中原工学院建筑工程学院，河南 郑州 450007)

应用高阶Cauchy-Born准则，通过建立新旧坐标系下平面矢量的坐标转换公式，推导新坐标系下应变梯度的关系式，为应变梯度传感器的应用提供了理论基础，为结构监测提供了新方法。

结构健康监测，光纤光栅传感器，应变梯度，高阶Cauchy-Born准则

0 引言

近年来，随着我国土木工程的繁荣发展，工程结构的健康监测问题成为一项越来越重要的研究。智能结构健康监测技术将先进传感技术与被测结构本身特性相结合，实现对结构服役状态、损伤程度的监测以及对损伤位置的判定[1]。在用于监测结构健康的传感器领域中，光纤光栅传感器发展迅速，广泛应用于土木工程结构健康监测中。目前，光纤光栅已经用来做成位移、应变、温度传感器，并且已相当成熟，而光纤光栅应变梯度传感器还处于探索阶段，虽然有人提出应变梯度传感器，但现在还没有发现关于光纤光栅应变梯度传感器得以实际应用的报道。

光纤光栅传感器质量轻、体积小，具有性能稳定、多参数测量、分布测量等优点，光纤光栅传感器的无电磁干扰、可测量多种信号、易于分布埋入结构和构成网络等特性，使其成为能够用于长期结构监测的理想传感元件[1]。这为开发新型传感器提供了可能。

大量疲劳试验表明，结构在其使用期限内70%的损伤始于初始裂纹。伴随着裂纹扩展，结构的强度与刚度也将不断劣化，最终导致突发性灾难事故。线弹性材料裂纹尖端的应变场具有r-1/2奇异性，应变梯度相对于应变其变化更加剧烈，具有更高阶的奇异性r-3/2[3]。相比传统的应变损伤识别，应变梯度的监测具有更加敏感、更早捕捉损伤的优势。

近年来，很多研究人员开始运用各种原理，注重于开发设计新型应变梯度传感器，并关注存在于大量生物材料、高分子材料以及晶体材料中的挠曲电效应[4,5]，目前已开发出几种可测量应变梯度的传感器，如钛酸锶钡(BST)应变梯度传感器[6,7]，应变梯度测量方面的研究还未见报道。若要将光纤光栅应变梯度传感器用于工程实际中，还需要解决一些问题，如已知该状态下的应变梯度，如何确定任意方向的应变梯度，最大应变梯度该如何确定等问题。本文应用高阶Cauchy-Born准则，通过建立新旧坐标系下平面矢量的坐标转换公式，推导新坐标系下应变梯度的表达式，为应变梯度传感器的使用提供理论基础。

1 Cauchy-Born准则

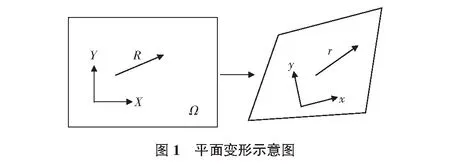
在结构变形中建立坐标系如图1所示，X=(X，Y)表示原始参考构形，x=(x，y)表示当前构形。结构从平面到曲面的变形映射由x=x(X)定义，其一阶和二阶变形梯度为：

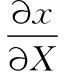
(1)

其中，i=1，2；J，K=1，2。

将一阶变形梯度F进行展开，形式如下：

(2)

将二阶变形梯度G进行展开，形式如下:

(3)

在经典Cauchy-Born准则中，变形前的矢量R和变形后的矢量r可通过一阶变形梯度F表示为[8]:

r=F·R

(4)

原始参考构形中矢量R的起点为X，变形后当前构形中的矢量r可以准确表示为：

r=x(X+R)-x(X)

(5)

对x(X+R)做关于X的泰勒级数展开，可得:

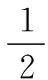
(6)

将式(6)代入式(5)，保留二阶项可得:

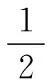
(7)

式(7)即为高阶Cauchy-Born准则下变形后的矢量近似表达式[10]。相对于经典Cauchy-Born准则，这里增加了一个基于二阶变形梯度的修正项。如果要提高近似解的精度，还可以附加更多的高阶项。

对弯曲或扭转的研究表明，杆件的最大应力往往发生于构件表层，由于构件表面一般为自由表面，即有一主应力等于零，因而从构件表层取出的微分单元体单元就接近二向应力状态。所以在工程监测中选择在构件表面测量与二向应力成比例的二向应变具有理论与埋设难易程度的实际意义。本文提出的应变梯度传感器可粘贴在构件表面工作，因而应变梯度的分析可以视为平面问题处理，可将光纤光栅看做方向矢量进行研究。

2 应变与应变梯度

在平面坐标系Oxy中，方向矢量R(X,Y)经变形成为r(x,y)。由应变的定义可知[11]：

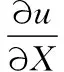
(8)

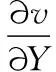
(9)

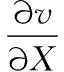
(10)

将式(8)～式(10)代入一阶应变梯度表达式(2)，可得:

本文研究基于的数据是1996—2017年，2018年的中美贸易战对中国石油安全也带来了影响，后期笔者将做进一步的研究。

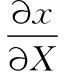
(11)

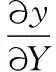
(12)

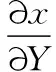
(13)

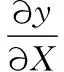
(14)

将式(11)～式(14)代入经典Cauchy-Born准则表达式(4)，展开写成分量形式为:

x=(1+εX)X+θXYY

(15)

y=θYXX+(1+εY)Y

(16)

将式(11)～式(14)代入高阶Cauchy-Born准则表达式(7)，展开写成分量形式为:

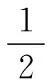
(17)

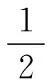
(18)

在坐标系OXY中，方向矢量R(X,Y)变形后方向为矢量r(x,y)，长度由|R|变为|r|，与X轴正方向夹角为α，则有:

X=|R|cosα,Y=|R|sinα

(19)

假设将坐标轴旋转α角(逆时针方向为正)，得到新坐标系Oxy(见图2)，方向矢量R(X,Y)变形后为r(x,y)，长度仍然由|R|变化为|r|，则有:

X|α=|R|,Y|α=0

(20)

将式(19)代入式(15)，式(16)得:

x=(1+εX)|R|cosα+θXY|R|sinα

(21)

y=θYX|R|cosα+(1+εY)|R|sinα

(22)

将式(20)代入式(15)，式(16)得:

x|α=(1+εX|α)·|R|,y|α=θYX|α·|R|

(23)

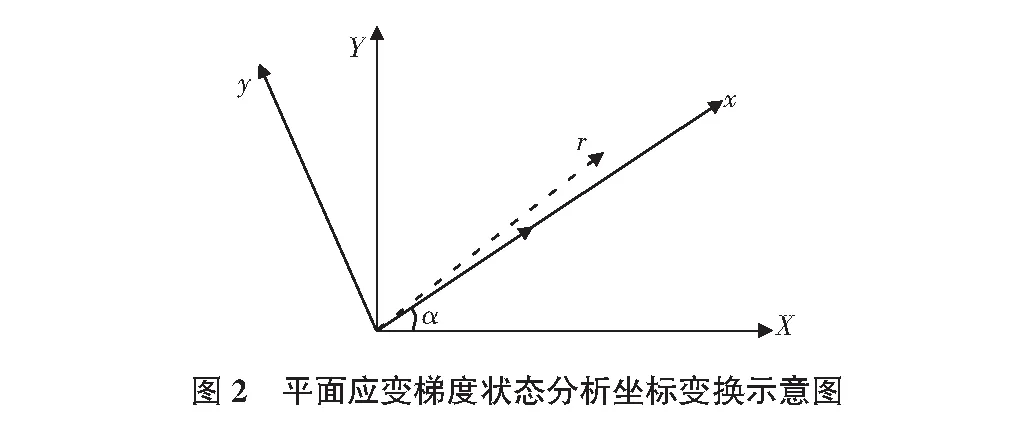
新旧坐标系下矢量坐标变换关系为:

x|α=xcosα+ysinα

(24)

y|α=-xsinα+ycosα

(25)

εX|α=εXcos2α+εYsin2α+γXYsinαcosα

(26)

式(26)即为平面应变状态下任意方向线应变表达式。

将式(19)代入式(17)，式(18)得:

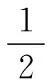
(27)

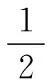
(28)

将式(20)代入式(17)，式(18)得:

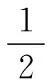
(29)

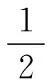
(30)

将式(27)～式(30)代入式(24)，化简得:

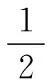
(31)

式(31)减去式(26)，化简得:

G111|α=G111cos3α+G222sin3α+
(G122+2G212)cosαsin2α+(G211+2G112)cos2αsinα

(32)

由式(32)可以计算分析α方向上的应变梯度，在平面上任意一点，通过6个应变梯度和角度关系即可表示出来该变形状态下任意方向的应变梯度。

当不考虑高阶梯度，应用经典Cauchy-Born准则，结论退化为平面应变状态下任意方向线应变表达式，这验证了式(32)推导结果的正确性。

由于应变梯度是最敏感的测量对象，通过对式(32)的应用，应变梯度的有效量测为掌控结构健康监测中裂缝的发生与生长情况提供了新途径。

3 结语

本文应用高阶Cauchy-Born准则，通过代入新旧坐标系下平面位移矢量的坐标转换公式，推导出了新坐标系下应变梯度的表达式，即任意方向上的应变梯度可通过该变形状态下的6个应变梯度和角度来表示。该理论为使用应变梯度理论制作光纤光栅应变梯度传感器进行结构健康监测的应用提供了理论基础。

为了更好地分析预测结构损伤，下一步我们将深入分析最大应变梯度该如何确定。

[1] 付兴权,干鹏飞.光纤健康监测技术在桥梁结构中的发展与应用[J].山西建筑,2015，41(26):166-167.

[2] 李宏男,李东升,赵柏东.光纤健康监测方法在土木工程中的研究与应用进展[J].地震工程与工程振动,2002,22(6):76-83.

[3] Staszewski D W,Lecturer.Monitoring on-line integrated technologies for operational reliability-monitor[J].Air & Space Europe,2000,2(4):67-72.

[4] 李 康,骆 英,徐晨光.基于BST微悬臂梁横向挠曲电系数的测定[J].压电与声光,2014(5):798-800.

[5] Baskaran S,He X,Chen Q,et al.Experimental studies on the direct flexoelectric effect in α-phase polyvinylidene fluoride films[J].Applied Physics Letters,2011,98(24):901-903.

[6] Kwon S R,Huang W B,Zhang S J,et al.Flexoelectric sensing using a multilayered barium strontium titanate structure[J].Smart Materials & Structures,2013,22(11):2870-2876.

[7] Huang W,Yan X,Kwon S R,et al.Flexoelectric strain gradient detection using Ba0.64Sr0.36TiO3 for sensing[J].Applied Physics Letters,2012,101(25):2903-2907.

[8] 赵亚溥.表面与界面物理力学[M].北京：科学出版社,2012.

[9] 范镜泓.材料变形与破坏的多尺度分析[M].北京:科学出版社,2008.

[10] Sun Y,Liew K M.The buckling of single-walled carbon nanotubes upon bending:The higher order gradient continuum and mesh-free method[J].Computer Methods in Applied Mechanics & Engineering,2008,197(33-40):3001-3013.

[11] 徐秉业.应用弹塑性力学[M].北京：清华大学出版社,1995.

Planestraingradientanalysisbasedonhigher-orderCauchy-Bornrule★

LvNaHouDongchangSunYuzhou

(SchoolofCivilEngineeringandArchitecture,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)

In this paper, by using the high-order Cauchy-Born rule and the coordinate transformation formula of plane vector in the new and old coordinate systems, the expression of strain gradient in the new coordinate system is derived, which provides a theoretical basis for the application of strain gradient sensors.

structure health monitoring， sensor, strain gradient, higher-order Cauchy-Born rule

TU196

：A

1009-6825(2017)24-0030-03

2017-06-15 ★ ：国家自然科学基金(11472316)；河南省科技创新人才项目(164200510020)

吕 娜(1991- )，女，在读硕士； 侯东昌(1991- )，男，在读硕士； 孙玉周(1974- )，男，博士，教授