也谈科学合理构建模型——对2013年高考浙江理综卷25题第(3)问争议的再分析

龚赛军(嵊州市高级中学 浙江 绍兴 312400)

也谈科学合理构建模型
——对2013年高考浙江理综卷25题第(3)问争议的再分析

龚赛军
(嵊州市高级中学 浙江 绍兴 312400)

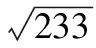
高考 物理模型 流体力学 参考系变换

1 题目

为了降低潜艇噪音，提高其前进速度，可用电磁推进器替代螺旋桨．潜艇下方有左、右两组推进器，每组由6个相同的、用绝缘材料制成的直线通道推进器构成，其原理示意图如图1所示．在直线通道内充满电阻率ρ=0.2 Ω·m的海水，通道中a×b×c=0.3 m×0.4 m×0.3 m的空间内，存在着由超导线圈产生的匀强磁场，其磁感应强度B=6.4 T,方向垂直通道侧面向外．磁场区域上、下方各有a×b=0.3 m×0.4 m的金属板M和N，当其与推进器专用直流电源相连后，在两板之间的海水中产生了从N到M，大小恒为I=1.0×103A的电流，设该电流只存在于磁场区域．不计电源内阻及导线电阻，海水密度ρm≈1.0×103kg/m3.

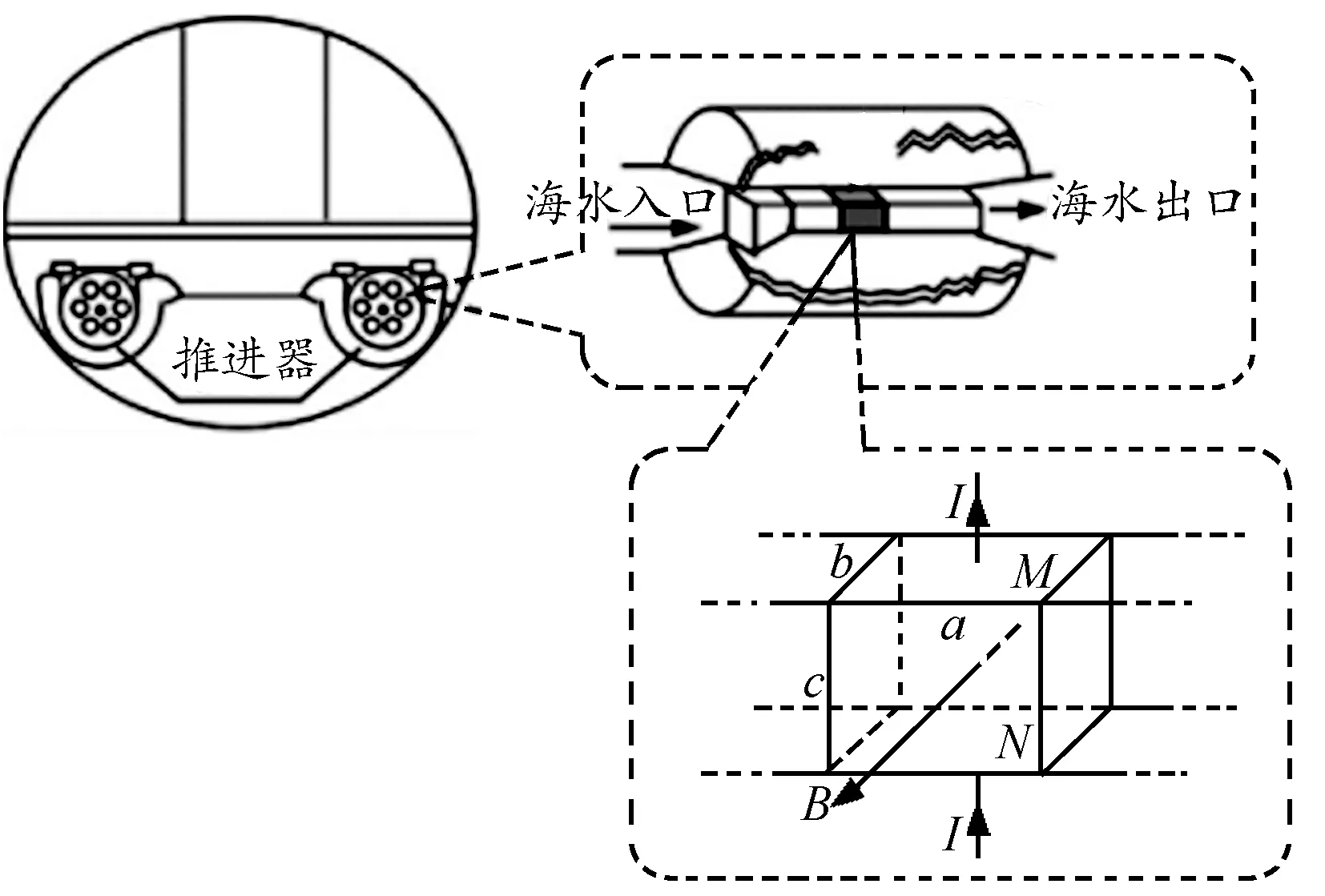
图1 题图

(1)略.

(2)略.

(3)当潜艇以恒定速度v0=30 m/s前进时，海水在出口处相对于推进器的速度v=34 m/s，思考专用直流电源所提供的电功率如何分配，求出相应功率的大小．

由于物理模型至关重要，所以有必要通过分析疑问来得出较科学的物理模型.下面首先澄清几个相关问题.

(1)管内液体流动是加速吗？如果不是，是一种什么运动？

答：不是.若管内液体流动是加速，那么管内各处流量将不同，从而导致出现真空，但因大气压的作用下不可能真空，特别是长时间下保持真空.

满足液体充满空间、管内任一截面处流量相等条件下管内液体必定是匀速运动，原因是质量守恒要求相等时间内管道进口进入的质量必须等于出口离开的质量，即磁流体推进器管道截面积相同，那么进入速度是等于离开速度的！

(2)管内液体为什么在安培力作用下仍然做匀速运动？管内液滴微元受力情况是怎样的？

因为所有的液滴被约束在管内，除了受到安培力以外还受到了管内前后截面压力的作用，当这个安培力与压力差平衡的时候管内液体就能够匀速运动.

管内液滴微元受力情况如图2所示.

图2 液滴受力示意图

这个问题可以通过一个理想模型来理解.有一根很长的自来水管竖直放置，上端连有一个水池，下端水龙头打开后，我们会认为竖直管内的水速度是一样的，就算受到重力作用.

(3)那么液滴在何处加速？为什么能加速？管道内匀速的速度大小大概与哪些因素有关？

液滴在管道进口前端(截面积变小)加速，如图3所示.

易分析出此处截面积变小，流量相同下流速在增大！

图3 截面积变化示意图

加速度大小与管口收缩梯度(坡度)有关，更与入口前端左右侧压强差有一定的关系.

因为液滴微元在出口处压强与环境压强一致，而从液滴微元受力分析图可以看出(存在安培力区域)越靠近左端压强越小，而管道入口前端左侧与环境压强一致.这样由于管道入口前端左侧压强大，入口右侧压强小，在压力差下海水在此加速.

管道内的速度大小与管道前端两侧压强差有关，而这个压强差与安培力大小以及管道的长度存在一定的关系.

(4)那么这个问题的真相是什么？解决的理论是什么？合理的结论是什么？

由上述可见，此类问题其实与中学物理所遇到的对象有很大不同，是一个连续流体问题，也就是流体力学问题.费因曼把忽略黏性的理想水的流动称为干(不考虑粘滞)水的流动.在有关流体的普遍理论中，人们必须从联系压强和密度的物态方程出发，即流体质量守恒(连续性方程[1])得出：在不可压缩下ρ是恒量.此类问题为定常流，由伯努利定理来解决，方程为

(1)

式中p为该处压强，ρ为流体密度，v为该处速度大小，若仅考虑重力作用φ=gz，g为重力加速度，z为相对参考平面的高度，如图4所示.

根据式(1)可以看出，在得出p，ρ，φ的基础上任何一处的v均可以求得.如果将安培力等效为重力，则可以将式(1)变换成

(2)

因为入口与出口均在大海(默认同一深度)，所以

p′=p

(3)

因等效重力仅在灰色区域，其高度差为a，所以

z-z′=a

(4)

因为安培力等于等效重力，所以

BIc=ρabcg′

(5)

由式(2)～(5)联立，可得

(6)

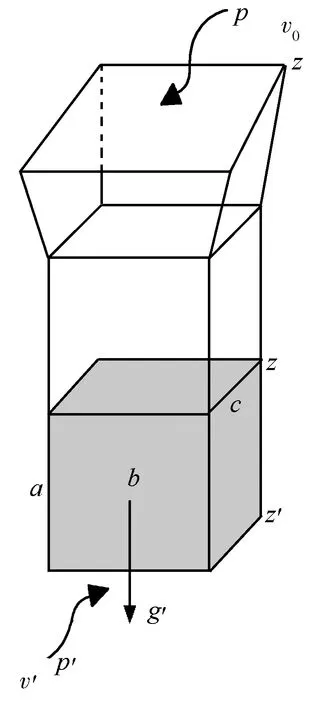
图4 等效重力示意图

这个才是真正的海水在出口处相对于推进器的速度！也就是原题干中v=34 m/s是多余且错误的，并且就是造成各种问题的源头.

2 常规解法验证

理论上利用牛顿运动定律、动能定理或者动量定理均可解答，并且在不同参考系下答案均自洽.动能定理可以规避很多繁琐细节，以艇为参考系物理模型理解相对简单.若将艇看作一个系统，这个系统消耗电能，一方面产生焦耳热，另一方面使一部分水动能增大，即可以将系统看作一个水泵.经过一段时间后，可等效为艇前方质量为ρbcv′Δt的水直接到了出口处，管内水没有变化.电源输出电压等于海水电阻压降(IR)和反电动势(Bav′)之和.由消耗电能等于增加焦耳热与水动能增加量，有

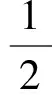
(7)

2.1以艇为参考系用牛顿运动定律分析及求解

为分析方便选取截面积为S0沿运动方向长度为d0的微元为研究对象，分为前端入口的加速运动和管内匀速运动.

对于管内的匀速运动，微元受到对应安培力等于两个侧面之间压强差(Δp0)乘截面积S0.那么有

(8)

那么整段压强差

(9)

为了问题简单，在前端特殊造型使得微元做匀加速运动，由于前端在大海连接，所以前端压强差也为Δp.在加速过程中必定会使微元面积和长度发生变化，但因为匀加速说明压差梯度为恒定值.若加速端长度为L，则微元加速度大小为

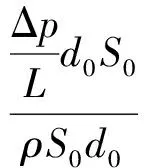
(10)

若截面积变化则长度随之变化，但乘积不变即加速度不变.由匀变速运动可得

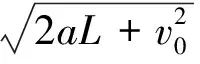
(11)

由式(10)、(11)可以得出

2.2以岸为参考系用牛顿运动定律分析及求解

根据上面2的分析，同样因为有安培力作用区域内做匀速运动计算得出压差与式(9)完全一致.假设前端长度也为L，则微元加速度大小也为式(10).微元前端入口速度变为零,设微元前端出口(进入方形管道)速度为v″,艇做速度为v0的匀速直线运动,水微元做初速度为零的匀加速运动,当微元到达前端后壁(开始匀速)时艇位移为x艇，水微元位移为x水.由图5可知

L=x艇+x水

(12)

x艇=v0t

(13)

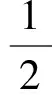
(14)

v″=at

(15)

由式(9)、(10)、(12)、(13)、(14)、(15)联立可得

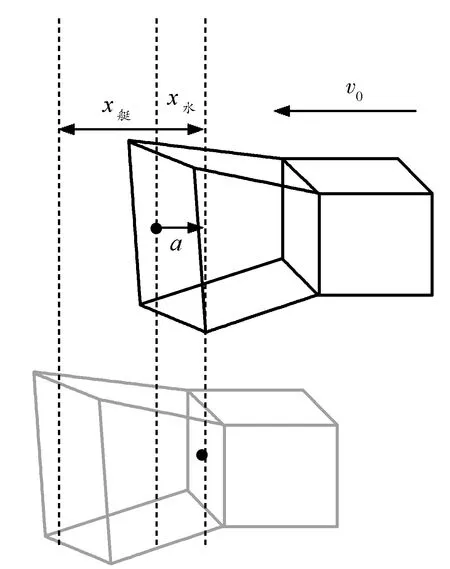
图5 以岸为参考系运动分析

2.3几点说明

以一个大整体水为研究对象应用动能定理，相当于应用质点系动能定理，忽略保守内力(水压力)做功是可以的.以微元为研究对象无论是动能定理还是牛顿运动定律均需考虑内部压力问题.动能定理、牛顿运动定律，包括动量定理在此题中本质其实是一样的.参考系的变化得出的结果是自洽的，甚至在非惯性参考系中(考虑惯性力做功).

2.3.1 文献[3]中的问题

(1)作用质量的表达式存在问题

m=ρmbcv水对地Δt

由极限法若v水对地非常小则Δt为一个不大的数，按照表达式,m接近零，显然是荒谬的.以潜艇为参考系，水出潜艇后假设速度不变且不分开，则经过潜艇的水(灰色)如图6所示.

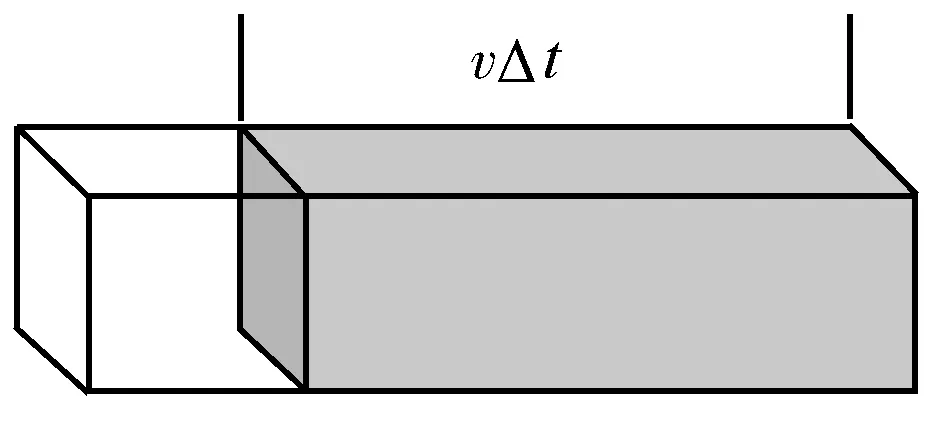
图6 潜艇参考系出水示意图

若以地面为参考系，则如图7所示.

图7 潜艇参考系出水示意图

可以看出官方解答与此文都仅仅考虑了地面参考系参考界面后方的水.

(2)电路模型存在问题，如图8所示.

图8 错误的电流方向

显然推进系统是电动机模型，即电流方向同向.

2.3.2 文献[4]中的问题

(1)文献[4]中桨作用的水的质量表达式与文献[3]存在同样问题.特别由于采用v=34 m/s，那么会有

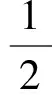
这样导致各种解答看上去完全自洽.

(2)文献[4]中的讨论3，研究对象存在问题.假定潜艇不动，在磁场区域内的海水移动，对此部分海水应用动能定理,如图9所示.

图9 框内海水在这部分海水整体未全部进入已经受安培力

因为移出潜艇部分的水(黑框内部分)与最左侧的海水在通过潜艇过程中受力完全一样的.这部分海水此时的安培力确实不等于BIc,但也需考虑框中水进入潜艇过程受力.可以等效为整体持续存在安培力BIc.因此本文在研究时采用整体(一段时间通过管道内所有水)和微元液滴两个模型分别研究.

2.3.3 文献[5]中的问题

(1)文中提出喷出海水质量为

m=ρmbcv0Δt

存在问题.

解法1：P1+P2+P3=(6.9×105+6×106+6.144×103)W=6.696 144×106W

解法2：P1+P2+P3=(6.9×105+6×106+6.144×103)W=6.696 14×106W

解法3：P2+P3=(6×106+6.97344×105)W=6.697 344×106W

解法4：P2+P3=(6×106+6.97344×105)W=6.697 344×106W

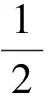
3 结束语

综上所述，模型建立确实需要全面考虑，特别需要科学合理.由于流体力学有别于质点力学，因此在大学物理中专门列出一个章节或者一门课程来展开教学,故在高考题中出现这样的命题是不合适的.另外由于中学物理默认地面为做功、动能等参考系，非地面参考系的动能定理应用就算是有经验的教师也难免出错，希望高考命题尽量避开.

1 费恩曼.费恩曼物理学讲义(新千年版).上海：上海科学技术出版社,2013.554～559

2 漆安慎，杜蝉英.力学 .北京：高等教育出版社,1997.352～357

3 袁张瑾.潜艇动力系统总功率的另两种计算方法.物理教学,2013(07):65～67

4 郑维鹏.模型建立要科学合理问题分析要多角度.物理通报，2016(03)：105～107

5 欧剑雄.高考物理试题效度证据的研究. 物理通报，2015(07)：89～90

TalkingaboutConstructingModelScientificallyandReasonably——ReanalysisonthePart3ofQuestion25ofZhejiangScienceandComprehensivePaperin2013CollegeEntranceExamination

Gong Saijun
(Shengzhou Senior Middle School, Shaoxing, Zhejiang 312400)

college entrance examination; physical model; hydromechanics; transformation of reference system

2017-02-24)