三角形全等条件的理解
2017-09-25杭永根
杭永根
三角形全等条件的理解
杭永根
判定三角形全等的方法有“边角边”“角边角”“角角边”“边边边”,对于直角三角形全等的判定,除了上述方法外还有“斜边、直角边”,如何理解这些三角形全等的条件呢?下面对判定三角形全等的条件加以剖析,供同学们学习时参考.
一、边角边(SAS)
对于这个判定方法,同学们要注意4点:
第一,这个判定方法是作为公理给出的,尽管我们可以用画图试验的方法来验证它,但验证不等于证明(下面几个判定方法也是如此).
第二,这个公理的条件是3个元素(两边和一对夹角)对应相等,即一个三角形的“边角边”对应着另一个三角形的“边角边”.这里“对应”两个字很重要,如果不注意,就可能出现下列情况:一个三角形是“边角边”,而另一个三角形是“边边角”,这样的两个三角形就不一定全等.
例如,图1中,AB=DE,∠B=∠E,BC=DF,但△ABC与△DEF就不全等.由此可知“对应”包含着顺序关系.
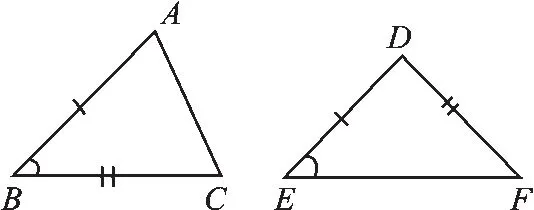
图1
第三,这个公理的条件中“相等的角”是指两条边的夹角(所以写成“边角边”),如果把夹角改成其中一边的对角(变成“边边角”),那么这两个三角形也不一定全等.
例如,图2中,虽然有∠B=∠B,AB=AB,AC= AE,但显然△ABC和△ABE并不全等.
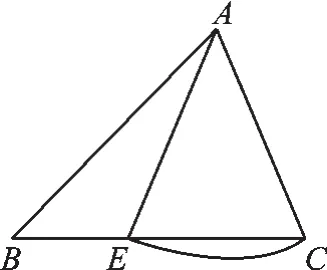
图2
第四,根据这个公理可知,有两条直角边对应相等的两个直角三角形全等.
二、角边角(ASA)
对于这个公理和推论,需要说明3点:
第一,这个公理的题设也是3个元素(两个角和一条夹边)对应相等,它是一个三角形的“角边角”对应另一个三角形的“角边角”.这里的“对应”仍然包含着顺序关系,不能含糊.
第二,“角边角”公理能够改变对应顺序,变成“角角边”或“边角角”,这时恰好是它的推论,只要有任意两个角和一边对应相等,这两个三角形就全等.但一定要注意“对应”二字.
如图3,∠B=∠E,∠C=∠F,AB=EF(这两边不是对应边),所以△ABC与△DEF不全等.
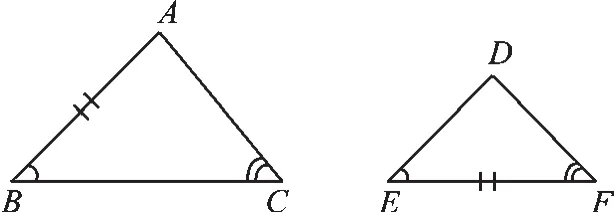
图3
第三,由这个公理可知,有一个锐角与一条边对应相等的两个直角三角形全等.
三、边边边(SSS)
对于这个判定方法要注意以下几点:
第一,这个判定方法的条件也是3个元素(三条边)对应相等,由于只有三角形的三条边,所以应用这个判定方法判定两个三角形全等时,对边的书写顺序要求不严格.
第二,这个判定方法表明了这样一个客观事实:只要三角形三条边的长度确定了,它的形状也就确定了.这个性质叫做三角形的稳定性.我们在生产和生活中,随处都可以见到三角形稳定性的应用.
四、斜边、直角边(HL)
判定两个直角三角形全等的方法有:“SAS”“ASA”“AAS”“SSS”“HL”.其中“HL”是直角三角形所特有的.分析“HL”定理,我们可以发现,它属于“SSA”型.但前面我们又已经知道,有两边及其中一边的对角对应相等的两个三角形不一定全等.那满足“SSA”型的两个三角形何时才能全等呢?
方法1:若两个三角形有两边及其中一边的对角对应相等,当这个角是直角时,这两个三角形全等.
方法2:若两个三角形有两边及其中一边的对角对应相等,当这个角是钝角时,这两个三角形全等.
方法2是说,在两个钝角三角形中,有两边对应相等,且这两条边之一是钝角的对边,则这两个三角形全等.如图4,在△ABC和△DEF中,AB= DE,BC=EF,∠ACB=∠DFE>90°,则△ABC≌△DEF.事实上,过B、E分别作射线AC、DF的垂线,垂足为M、N,由∠ACB=∠DFE,得∠BCM=∠EFN,又BC=EF,所以Rt△BCM≌Rt△EFN(AAS),所以BM=EN.再由“HL”可以证明Rt△ABM≌Rt△DEN,得∠A=∠D,再证明△ABC≌△DEF就容易了.
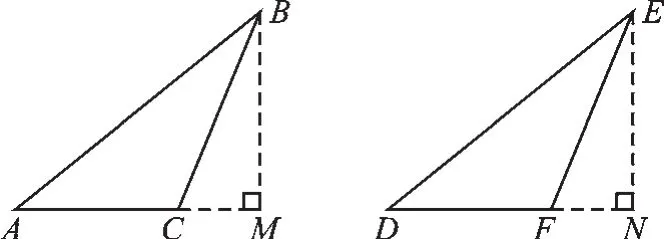
图4
方法3:若两个三角形有两边及其中一边的对角对应相等,当这两边的夹角是钝角时,则这两个三角形全等.
如图5,在△ABC和△DEF中,AC=DF,BC= EF,∠ACB>90°,∠DFE>90°,∠A=∠D,则△ABC≌△DEF.事实上,分别过C、F作CM、FN的垂线,垂足分别为M、N,由∠A=∠D,AC=DF,可得Rt△ACM≌Rt△DFN,有CM=FN,再由CM=FN,BC=EF,由“HL”可得Rt△BCM≌Rt△EFN,有∠B=∠E,再证明△ABC≌△DEF就容易了.
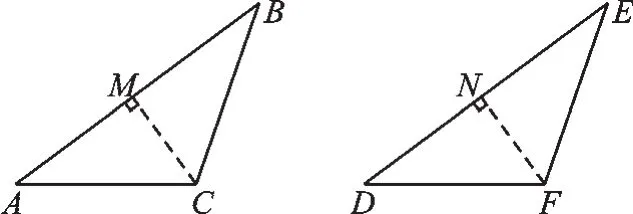
图5
由上面的探索可知,满足“SSA”的两个非锐角三角形一定全等.
方法4:若两个三角形有两边及其中一边的对角对应相等,当两个三角形都是锐角三角形时,这两个三角形全等.
如图6,在锐角△ABC和锐角△DEF中,AB= DE,BC=EF,∠ACB=∠DFE,则△ABC≌△DEF.事实上,如图6,分别过点B、E作AC、DF的垂线,垂足为M、N,由∠ACB=∠DFE,BC=EF,得Rt△BCM≌Rt△EFN(AAS),所以BM=EN;再由“HL”可以证明Rt△ABM≌Rt△DEN,得∠A=∠D,再证明△ABC≌△DEF就容易了.

图6
你还有其他的方案吗?请写出来,与你的同伴进行交流.
(作者单位:江苏省兴化市戴泽初级中学)
